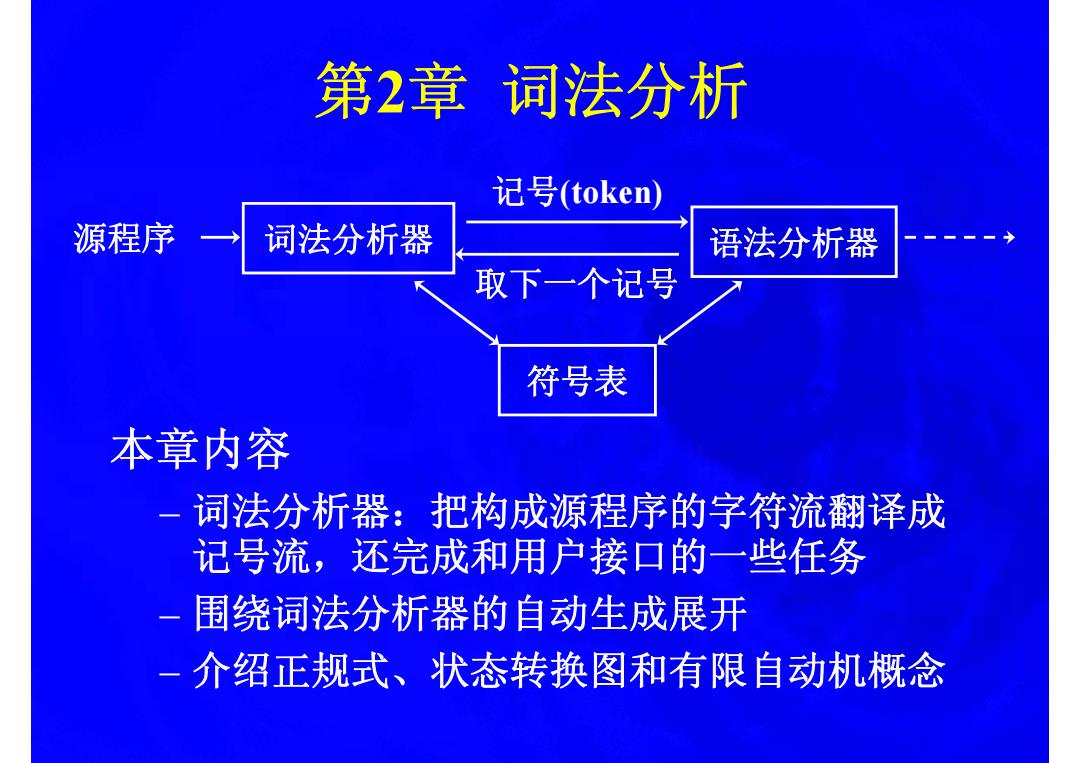
第2章词法分析 记号(token) 源程序 词法分析器 语法分析器 取下一个记号 符号表 本章内容 词法分析器:把构成源程序的字符流翻译成 记号流,还完成和用户接口的一些任务 一围绕词法分析器的自动生成展开 一介绍正规式、状态转换图和有限自动机概念
第2章 词法分析 词法分析器 语法分析器 记号(token) 源程序 词 分析 取下一个记号 符号表 本章内容 – 词法分析器:把构成源程序的字符流翻译成 记号流,还完成和用户接口的一些任务 – 围绕词法分析器的自动生成展开 – 介绍正规式、状态转换图和有限自动机概念

2.1词法记号及属性 2.1.1词法记号、模式、词法单元 记号名 词法单元例举 模式的非形式描述 if if 字符i,f for for 字符f,0,r relation <,<=,== <或<=或==或. id sum, count,D5 由字母开头的字母数字串 number 3.1,10,2.8E12 任何数值常数 literal “seg.error" 引号“和”之间的任意字 符串,但引号本身除外
2 1. 词法记号及属性 2.1.1 词法记号、模式、词法单元 记号名 词法单元例举 模式的非形式描述 if if 字符i, f for for 字符f, o, r relation < , <= , == , … < 或 <= 或 == 或 … id sum, count, D5 由字母开头的字母数字串 由字母开头的字母数字串 number 3.1, 10, 2.8 E12 任何数值常数 literal “seg. error” 引号“和”之间的任意字 符串,但引号本身除外

2.1词法记号及属性 历史上词法定义中的一些问题 一忽略空格带来的困难 (如Fortrani语言) D08I=3.75 D08I=3.75 D08I=3,75 关键字不保留(如Fortran语言) IF THEN THEN THEN-ELSE:ELSE 关键字、保留字和标准标识符的区别 一保留字是语言预先确定了含义的词法单元 标准标识符也是预先确定了含义的标识符,但程 序可以重新声明它的含义
2 1. 词法记号及属性 • 历史上词法定义中的一些问题 – 忽略空格带来的困难 忽略空格带来的困难(如 F t or ran语言) DO 8 I 3. 75 DO8I 3. 75 DO 8 I 3, 75 – 关键字不保留(如 Fortran Fortran语言) IF THEN THEN THEN=ELSE;ELSE … • 关键字、保留字和标准标 符识 的区别 – 保留字是语言预先确定了含义的词法单元 – 标准标识符也是预先确定了含义的标识符,但程 序可以重新声明它的含义

2.1词法记号及属性 2.1.2词法记号的属性 position initial rate 60 的记号和属性值: id,指向符号表中position条目的指针) (assign op) id,指向符号表中initial条目的指针〉 <add op) id,指向符号表中rate条目的指针〉 〈nul_op〉 number,整数值60
2 1. 词法记号及属性 2.1.2 词法记号的属性 posii i ii ition = initial + rate 60 的记号 属性值 和 : id,指向符号表中position条目的指针 assign _ op id,指向符号表中initial条目的指针 add_op id,指向符号表中rate条目的指针 mul_ op number,整数值60

2.1词法记号及属性 2.1.3词法错误 一词法分析器对源程序采取非常局部的观点 -例:难以发现下面的错误 fi(a=f(x)).… 在实数是a.b格式下,可以发现下面的错误 123.x 紧急方式的错误恢复 删掉当前若干个字符,直至能读出正确的记号 错误修补 进行增、删、替换和交换字符的尝试
2 1. 词法记号及属性 2.1.3 词法错误 – 词法分析 对 程序采 非常 部的 点 法分析器对源程序采取非常局部的观点 – 例:难以发现下面的错误 fi (a == f (x) ) … – 在实数是a.b格式下,可以发现下面的错误 123.x – 紧急方式的错误恢复 删掉当前若干个字符,直至能读出正确的记号 – 错误修补 进行增、删、替换和交换字符的尝试

2.2词法记号的描述与识别 2.2.1串和语言 字母表:符号的有限集合,例:∑={0,1} -串:符号的有穷序列,例:0110,e 一语言:字母表上的一个串集 {8,0,00,000,.},{8,☑ 一句子:属于语言的串 串的运算 -连接(积) Xy,SE=ES=S 幂 s0为e,s为sls(i>0》
2 2. 词法记号的描述与识别 2.2.1 串和语言 – 字 表母 :符号的有 集合 符号的有限集合, 例: = { 0, 1} – 串:符号的有穷序列 符号的有穷序列,例:0110, – 语言:字母表上的一个串集 {, 0, 00, 000, …}, {}, – 句子:属于语言的串 • 串的运算 – 连接(积) xy,s = s = s –幂 s0为 si为si -1 –幂 s0为,si为si 1s(i > 0)

2.2词法记号的描述与识别 语言的运算 - 并: LUM={s|S∈L或s∈M} 连接: LM={St|S∈L且t∈MW 幂 L0是{ε,L是L-1Z -闭包: L*=LOULIU I2U... - 正闭包: L+=IIUI2U... 例 L:{A,B,,Z,4,b,,z},D:{0,1,…,9} L U D,LD,L,L",L(L U D)",D
2 2. 词法记号的描述与识别 • 语言的运算 – 并: L ∪ M = {s | s L 或 s M } – 连接: LM = {st | s L 且 t M} – 幂: L0是{},Li是Li -1L – 闭包: L = L0 ∪ L1 ∪ L2 ∪ … – 正闭包: L+ 正闭包: L = L1 ∪ L2 ∪ … • 例 L: { A, B, …, Z, a, b, …, z }, D: { 0, 1, …, 9 } L ∪ D LD L6 L* L(L ∪ D ) L ∪ D * D+ , LD, L6, L , L(L ∪ D ) , D+

2.2词法记号的描述与识别 2.2.2正规式 正规式用来表示简单的语言,叫做正规集 正规式 定义的语言 备注 (e} 0 a a∈∑ (r)(s) L(r)UL(s) r和s是正规式 (r)s) L(r)L(s) 和s是正规式 (r)' (L(r)) r是正规式 (r) L(r) 是正规式 (a(b))(c)可以写成ab1c
2 2. 词法记号的描述与识别 2.2.2 正规式 正规式用来表示简单的语言,叫做正规集 正规式 定义的语言 备注 {} a {a} a (r)|(s) L(r)∪L(s) r和s是正规式 (r)(s) L(r)L(s) r和s是正规式 (r)* (L(r))* r是正规式 (r) L(r) r是正规式 ((a) (b)*)| (c)可以写成ab*| c

2.2词法记号的描述与识别 正规式的例子Σ={a, -a b a,by -(a b)(a b) faa,ab,ba,bby aa ab ba bb Kaa,ab,ba,bby - 由字母构成的所有串集,含e -(ab) 由a和b构成的所有串集,含ε 复杂的例子 (001111((01110)(00111)*(01110)))* 句子:01001101000010000010111001
2 2. 词法记号的描述与识别 • 正规式的例子 = {a, b} – a | b {a, b} – (a | b) (a | b ) {aa, ab, ba, bb} – aa | ab | ba | bb {aa, ab, ba, bb} – a * 由字母a构成的所有串集,含 – (a | b) (a | b)* 由a和b构成的所有串集 构成的所有串集,含 • 复杂的例子 ( 00 | 11 | ( (01 | 10) (00 | 11) (01 | 10) ) ) 句子:01001101 01001101000010000010 10000010111001

2.2词法记号的描述与识别 2.2.3正规定义 对正规式命名,使表示简洁 d→r1 2→r2 dn→rm -各个4,的名字都不同 -每个r:都是ΣU{d,,,d1》上的正规式
2 2. 词法记号的描述与识别 2.2.3 正规定义 – 对正规式命名,使表示简洁 d1 r1 d2 r2 ... dn rn – 各个di的名字都不同 – 每个ri都是 ∪{d1, d2, …, di-1 }上的正规式