
敦案 第七章图 程序设计—数据结构 图的遍历算法及其应用 目录 第7章图. 1 7.1图的定义和基本术语 7.2图的存储和创建. 2 7.2.1图的存储表示 7.2.2图的创建 _5 7.3图的遍历… 5 7.3.1深度优先搜索 5 7.3.2广度优先搜索 7.4遍历算法的应用.… 6 8 7.4.1应用问题概述 8 7.4.2求一条包含图中所有顶点的简单路径. 8 7.4.3求距v0的各顶点中最短路径长度最长的一个顶点 9 7.5图的连通性问题.… ,。。。2-。-。。。。,。。。。。。。。。,。。。,。。。,。,。,。,。。,。。。,.。。。,。 7.5.1无向图的连通分量和生成树10 7.5.2最小生成树.… 2 7.6有向无环图及其应用 12 文档编号引 完成时间 完成人张昱 修改时间20026-6 第0页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 0 页 目 录 第7章 图...............................................................................................................................1 7.1 图的定义和基本术语.................................................................................................1 7.2 图的存储和创建........................................................................................................2 7.2.1 图的存储表示..................................................................................................2 7.2.2 图的创建.........................................................................................................5 7.3 图的遍历..................................................................................................................5 7.3.1 深度优先搜索..................................................................................................5 7.3.2 广度优先搜索..................................................................................................6 7.4 遍历算法的应用........................................................................................................8 7.4.1 应用问题概述..................................................................................................8 7.4.2 求一条包含图中所有顶点的简单路径...............................................................8 7.4.3 求距v0的各顶点中最短路径长度最长的一个顶点.............................................9 7.5 图的连通性问题......................................................................................................10 7.5.1 无向图的连通分量和生成树...........................................................................10 7.5.2 最小生成树...................................................................................................12 7.6 有向无环图及其应用...............................................................................................12

教黎 第七章图 程序设计—数据结构 图的遍历算法及其应用 第7章图 7.1图的定义和基本术语 1、图的特征 任意两个数据元素之间都可能相关。结点之间的关系是多对多的。 G=(V,{E}) 2、基本术语 结点:顶点 结点间的关系:无向图:边(yw),v与w互为邻接点,边(y,w)依附于顶点y,w,边(v,w) 和顶点y,w相关联 v的度:和v相关联的边的数目。 有向图:弧,v弧尾,w弧头,顶点v邻接到顶点w,顶点w邻接 自顶点v,弧和顶点y,相关联。 v的入度:以v为弧头的弧的数目:v的出度:以v为弧尾的弧的数目: v的度:v的入度与出度之和。 路径、回路(环、简单路径、简单回路(简单环) 连通性:若从顶点v到顶点v有路径,则称v和v是连通的 图的规模:顶点数n、边(弧)数、项点的度(有向图:入度/出度) 子图:G=(P,{E}),G=(V,{E),若VcV且EcE,则称G是G的子图。 图的分类: 1)关系的方向性(无向/有向)、关系上是否有附加的数一一权(图/网) 有向图、无向图、有向网、无向网 2)边(弧)数:完全图(边数=n(r1)/2的无向图)、有向完全图(弧数=n(m1)的有向图) 稀疏图(enlogn) 3)连通性:无向图:连通图(任意两顶点都是连通的)、连通分量(极大连通子图)、生成树极 小连通子图)、生成森林 有向图:强/弱连通图、强连通分量、生成树(极小连通子图)、生成森林 3、抽象数据类型定义 ADT Graph 数据对象V:V是具有相同特性的数据元素的集合,称为顶点集。 数据关系R: R=VR) VR={WweV且P(W,w),表示从v到w的弧,谓词P(V,w) 定义了弧的意义或信息} 基本操作: CreateGraph(&G.V.VR) 初始条件:V是图的顶点集,VR是图中弧的集合 操作结果:按V和VR的定义构造图G DestroyGraph(&G) 初始条件:图G存在 操作结果:销毁图G LocateVex(G,u) 初始条件:图G己存在,u和G中顶点有相同特征 文档编号 完成时间 完成人张昱 修改时间20026-6 第1页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 1 页 第7章 图 7.1 图的定义和基本术语 1、图的特征 任意两个数据元素之间都可能相关。结点之间的关系是多对多的。 G = (V,{E}) 2、基本术语 结点: 顶点 结点间的关系:无向图:边( v, w ),v 与 w 互为邻接点,边( v, w )依附于顶点 v, w,边( v, w ) 和顶点 v, w 相关联 v 的度:和 v 相关联的边的数目。 有向图:弧,v 弧尾,w 弧头,顶点 v 邻接到顶点 w,顶点 w 邻接 自顶点 v,弧和顶点 v,w 相关联。 v 的入度:以 v 为弧头的弧的数目;v 的出度:以 v 为弧尾的弧的数目; v 的度:v 的入度与出度之和。 路径、回路(环)、简单路径、简单回路(简单环) 连通性:若从顶点 v 到顶点 v’有路径,则称 v 和 v’是连通的 图的规模:顶点数 n、边(弧)数 e、顶点的度(有向图:入度/出度) 子图:G’= (V’,{E’}), G = (V,{E}),若 V’V 且 E’ E,则称 G’是 G 的子图。 图的分类: 1)关系的方向性(无向/有向)、关系上是否有附加的数——权(图/网) 有向图、无向图、有向网、无向网 2)边(弧)数:完全图(边数= n ( n-1 ) / 2 的无向图)、有向完全图(弧数= n ( n-1)的有向图) 稀疏图(enlogn) 3)连通性:无向图:连通图(任意两顶点都是连通的)、连通分量(极大连通子图)、生成树(极 小连通子图)、生成森林 有向图:强/弱连通图、强连通分量、生成树(极小连通子图)、生成森林 3、抽象数据类型定义 ADT Graph{ 数据对象 V:V 是具有相同特性的数据元素的集合,称为顶点集。 数据关系 R: R = {VR} VR = {|v, wV且P(v, w),表示从v到w的弧,谓词P(v,w) 定义了弧的意义或信息} 基本操作: CreateGraph(&G, V, VR) 初始条件:V 是图的顶点集,VR 是图中弧的集合 操作结果:按 V 和 VR 的定义构造图 G DestroyGraph(&G) 初始条件:图 G 存在 操作结果:销毁图 G LocateVex( G, u ) 初始条件:图 G 已存在,u 和 G 中顶点有相同特征

敦黎 第七章图 程序设计—数据结构 图的遍历算法及其应用 操作结果:若G中存在顶点u,则返回该项点在图中位置,否则返回其 它信息 GetVex(G.v) 初始条件:图G存在,v是G中某个顶点 操作结果:返回ⅴ的值 PutVex(&G,v,value) 初始条件:图G存在,v是G中某个顶点 操作结果:对v赋值value FirstAdjVex(G,v) 初始条件:图G存在,V是G中某个顶点 操作结果:返回ⅴ的第一个邻接顶点。若顶点在G中没有邻接顶点,则 返回“空” NextAdjVex(G,v,w) 初始条件:图G存在,v是G中某个顶点,w是v的邻接顶点 操作结果:返回v的(相对于w的)下一个邻接顶点。若w是v的最后一 个邻接点,则返回“空” InsertVex(&G.v) 初始条件:图G存在,ⅴ和G中顶点有相同特征 操作结果:在图中增添新顶点ⅴ Delete Vex(&G,v) 初始条件:图G存在,ⅴ是G中某个顶点 操作结果:删除G中顶点V及其相关的弧 InsertArc(&G,v,w) 初始条件:图G存在,v和w是G中两个顶点 操作结果:在图G中增添弧,若G是无向的,则还应增添对称弧 DeleteArc(&G,v,w) 初始条件:图G存在,v和w是G中两个顶点 操作结果:删除G中的弧<V,w心,若G是无向的,则还应删除对称弧 DFSTraverse(G,v,visit()) 初始条件:图G存在,v是G中某个顶点,vsit是对顶点的应用函数 操作结果:从顶点v起深度优先遍历图G,并对每个顶点调用函数visit() 一次且至多一次。一旦visit()失败,则操作失败 BFSTraverse(G,v,visit()) 初始条件:图G存在,v是G中某个顶点,vsit是对顶点的应用函数 操作结果:从顶点v起广度优先遍历图G,并对每个顶点调用函数visit() 一次且至多一次。一旦visit()失败,则操作失败 ADT Graph 7.2图的存储和创建 7.2.1图的存储表示 1、图的存储表示分析 ,顶点之间的关系是多对多的(m:n),由于m和n都是不定的,无法给出一个这种多对多 的关系向线性关系的映射公式 ∴图中的关系不能通过顺序映像(即通过顶点之间的存储位置反映顶点之间的逻辑关系)反 文档编号 完成时间 完成人张昱 修改时间20026-6 第2页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 2 页 操作结果:若 G 中存在顶点 u,则返回该顶点在图中位置,否则返回其 它信息 GetVex(G, v ) 初始条件:图 G 存在,v 是 G 中某个顶点 操作结果:返回 v 的值 PutVex(&G, v, value) 初始条件:图 G 存在,v 是 G 中某个顶点 操作结果:对 v 赋值 value FirstAdjVex(G, v) 初始条件:图 G 存在,v 是 G 中某个顶点 操作结果:返回 v 的第一个邻接顶点。若顶点在 G 中没有邻接顶点,则 返回“空” NextAdjVex(G, v, w) 初始条件:图 G 存在,v 是 G 中某个顶点,w 是 v 的邻接顶点 操作结果:返回 v 的(相对于 w 的)下一个邻接顶点。若 w 是 v 的最后一 个邻接点,则返回“空” InsertVex(&G, v) 初始条件:图 G 存在,v 和 G 中顶点有相同特征 操作结果:在图中增添新顶点 v DeleteVex(&G, v) 初始条件:图 G 存在,v 是 G 中某个顶点 操作结果:删除 G 中顶点 v 及其相关的弧 InsertArc(&G, v, w) 初始条件:图 G 存在,v 和 w 是 G 中两个顶点 操作结果:在图 G 中增添弧,若 G 是无向的,则还应增添对称弧 DeleteArc(&G, v, w) 初始条件:图 G 存在,v 和 w 是 G 中两个顶点 操作结果:删除 G 中的弧,若 G 是无向的,则还应删除对称弧 DFSTraverse(G, v, visit( )) 初始条件:图 G 存在,v 是 G 中某个顶点,visit 是对顶点的应用函数 操作结果:从顶点 v 起深度优先遍历图 G,并对每个顶点调用函数 visit( ) 一次且至多一次。一旦 visit( )失败,则操作失败 BFSTraverse(G, v, visit( )) 初始条件:图 G 存在,v 是 G 中某个顶点,visit 是对顶点的应用函数 操作结果:从顶点 v 起广度优先遍历图 G,并对每个顶点调用函数 visit( ) 一次且至多一次。一旦 visit( )失败,则操作失败 }ADT Graph 7.2 图的存储和创建 7.2.1 图的存储表示 1、图的存储表示分析 ∵顶点之间的关系是多对多的(m : n),由于 m 和 n 都是不定的,无法给出一个这种多对多 的关系向线性关系的映射公式 ∴图中的关系不能通过顺序映像(即通过顶点之间的存储位置反映顶点之间的逻辑关系)反

第七章图 程序设计—数据结构 图的遍历算法及其应用 映:必须另外引入存储空间反映顶点之间的邻接关系。 图的存储结构:1)顶点信息:2)边(弧)信息:3)整体信息:顶点数、边(弧)数、图的种 类(有向图、无向图、有向网、无向网) 顶点集的存储:图的应用中,顶点集动态变化的几率十分小 ∴.顶点集可以采用顺序表存储,按预先估计的最大顶点数分配空间 (顺序表和链表:若数据元素集是静态的,采用顺序表要好(随机存取): 若数据元素集是动态的,则采用链表要好(动态分配与释放)) #define MAX VERTEX NUM 20 体最大顶点数*/ 注意:顺序表与顺序映像之间的区别 关系集的存储:在顶点确定的情况下,边或弧的数目也是不定的:且在实际应用中,可能 会改变图中顶点之间的关系。 邻接矩阵表示法:矩阵中的第ⅰ行第j列的元素反映图中第i个顶点到第 j个顶点是否存在弧:若存在,其附加的信息是什么。 邻接表表示法:将每一顶点的邻接点位置串成一个链,称为邻接表。对于 有向图/网来说,该邻接表反映的是顶点的出边表。 typedef enum(DG,DN,AG,AN)GraphKind; 体{有向图,有向网,无向图,无向网}*/ 2、邻接矩阵表示法(数组表示法) 无向图网:对称矩阵 有向图/网:非必是对称矩阵 图:邻接关系用1/0表示 网:邻接关系需要进一步反映权值,用NFINITY表示无穷大,反映顶点之间无邻接关系 #define INT MAX 32767 体最大整数 * #define INFINITY INT MAX 1)邻接矩阵 typedef struct ArcCell int adj; ∥顶点间关系,无权图:0-不相邻,1-相邻 ∥有权图,权值,NFINITY.不相邻 InfoType *info; ∥该弧相关信息的指针 }ArcCell,AdjMatrix[MAX VERTEX NUM][MAX_VERTEX_NUM]; 2) 图的整体结构 typedef struct{ VertexType vexs[MAX VERTEX NUM]; 体有效的顶点下标从0开始*/ AdiMatrix arcs: *关系集 int vexnum,arcnum; /体顶点数、边弧数 GraphKind kind; /体图的种类 */ MGraph; 3、邻接表表示法 无向图/网:边表,表结点的个数为边数的两倍 有向图网:出边表,表结点的个数为弧数 1)邻接表的表结点 typedef struct ArcNode int adivex;/体弧所指向的顶点的位置/ struct ArcNode *nextarc:体指向下一条弧的指针*/ InfoType *info; }ArcNode; 文档编号 完成时间 完成人张昱 修改时间20026-6 第3页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 3 页 映;必须另外引入存储空间反映顶点之间的邻接关系。 图的存储结构:1)顶点信息;2)边(弧)信息;3)整体信息:顶点数、边(弧)数、图的种 类(有向图、无向图、有向网、无向网) 顶点集的存储:∵图的应用中,顶点集动态变化的几率十分小 ∴顶点集可以采用顺序表存储,按预先估计的最大顶点数分配空间 (顺序表和链表:若数据元素集是静态的,采用顺序表要好(随机存取); 若数据元素集是动态的,则采用链表要好(动态分配与释放)) #define MAX_VERTEX_NUM 20 /* 最大顶点数 */ 注意:顺序表与顺序映像之间的区别 关系集的存储:在顶点确定的情况下,边或弧的数目也是不定的;且在实际应用中,可能 会改变图中顶点之间的关系。 邻接矩阵表示法:矩阵中的第 i 行第 j 列的元素反映图中第 i 个顶点到第 j 个顶点是否存在弧;若存在,其附加的信息是什么。 邻接表表示法:将每一顶点的邻接点位置串成一个链,称为邻接表。对于 有向图/网来说,该邻接表反映的是顶点的出边表。 typedef enum{DG, DN, AG, AN} GraphKind; /*{有向图,有向网,无向图,无向网}*/ 2、邻接矩阵表示法(数组表示法) 无向图/网:对称矩阵 有向图/网:非必是对称矩阵 图:邻接关系用 1/0 表示 网:邻接关系需要进一步反映权值,用 INFINITY 表示无穷大,反映顶点之间无邻接关系 #define INT_MAX 32767 /* 最大整数 */ #define INFINITY INT_MAX 1) 邻接矩阵 typedef struct ArcCell{ int adj; // 顶点间关系,无权图:0-不相邻,1-相邻 // 有权图,权值,INFINITY-不相邻 InfoType *info; // 该弧相关信息的指针 }ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; 2) 图的整体结构 typedef struct { VertexType vexs[MAX_VERTEX_NUM]; /* 有效的顶点下标从 0 开始 */ AdjMatrix arcs; /* 关系集 */ int vexnum, arcnum; /* 顶点数、边/弧数 */ GraphKind kind; /* 图的种类 */ }MGraph; 3、邻接表表示法 无向图/网:边表,表结点的个数为边数的两倍 有向图/网:出边表,表结点的个数为弧数 1) 邻接表的表结点 typedef struct ArcNode{ int adjvex; /* 弧所指向的顶点的位置 */ struct ArcNode *nextarc; /* 指向下一条弧的指针 */ InfoType *info; }ArcNode;
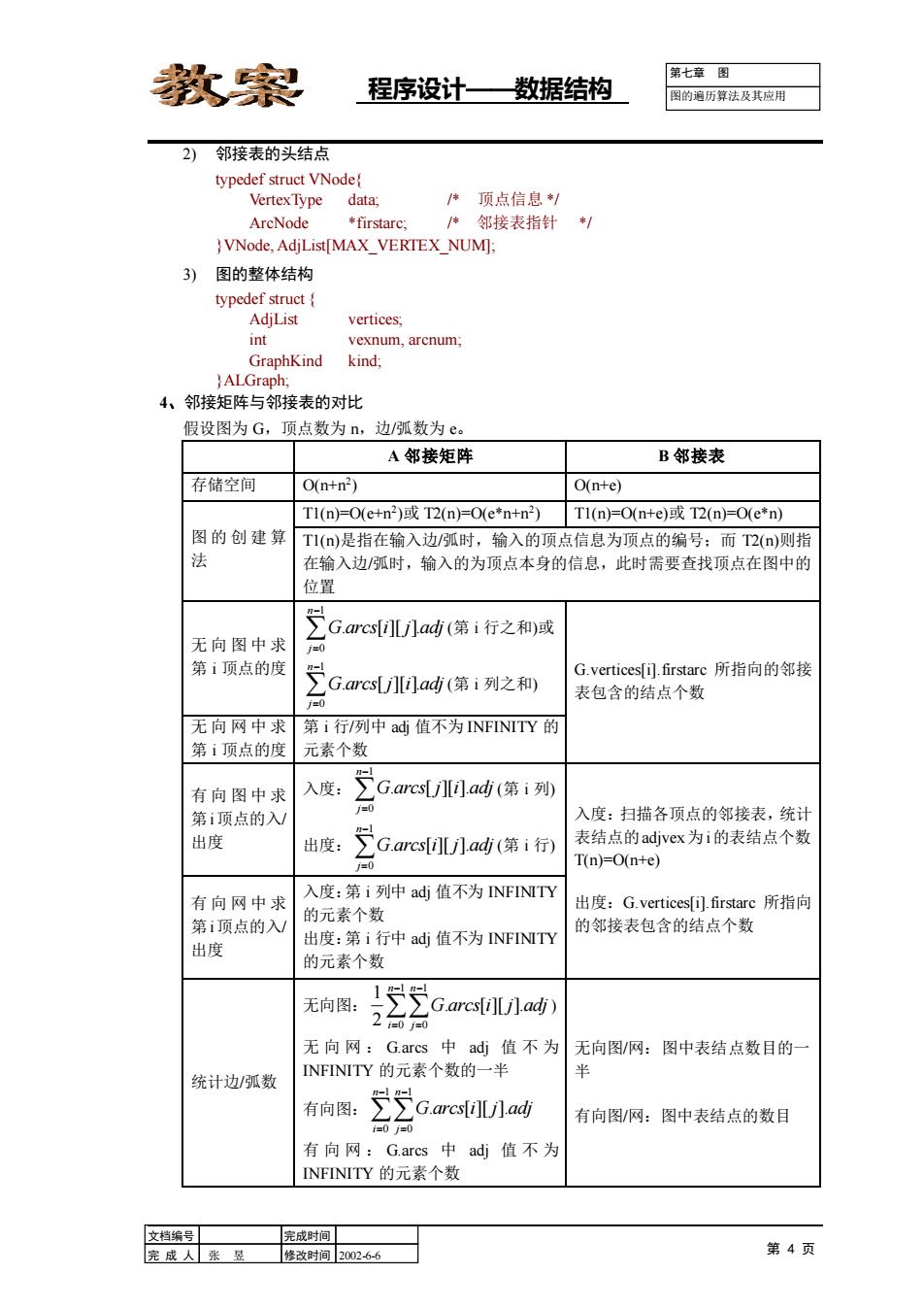
教黎 第七章图 程序设计—数据结构 图的遍历算法及其应用 2) 邻接表的头结点 typedef struct VNode! Vertex Type data; 体顶点信息制 ArcNode *firstarc; 体邻接表指针*/ }VNode,AdjList[MAX VERTEX NUM]; 3)图的整体结构 typedef struct{ AdjList vertices; int vexnum,arcnum; GraphKind kind; }ALGraph; 4、邻接矩阵与邻接表的对比 假设图为G,顶点数为n,边/弧数为e。 A邻接矩阵 B邻接表 存储空间 0(n+n2) O(n+e) T1(n)=0(e+n2)或T2(n=0(e*n+n2) T1(n)=0(n+e)或T2(n)=0(e*n) 图的创建算 T1(n)是指在输入边/弧时,输入的顶点信息为顶点的编号:而T2(n)则指 法 在输入边弧时,输入的为顶点本身的信息,此时需要查找顶点在图中的 位置 GarcM小a(第i行之利成 无向图中求 j-0 第ⅰ顶点的度 cana时第i列之利 G.vertices[i.firstarc所指向的邻接 表包含的结点个数 j=0 无向网中求 第i行/列中ad值不为NFINITY的 第ⅰ顶点的度 元素个数 有向图中求 入度: acU0a(第i列 第i顶点的入 0 入度:扫描各顶点的邻接表,统计 出度 出度: GaresiUJad(第i行 表结点的adjvex为i的表结点个数 /0 T(n)=O(n+e) 有向网中求 入度:第i列中ad值不为NFINITY 出度:G.vertices[i).firstarc所指向 第i顶点的入/ 的元素个数 的邻接表包含的结点个数 出度 出度:第i行中adi值不为NFINITY 的元素个数 无向图: GonaEad 无向网:G.arcs中adj值不为 无向图/网:图中表结点数目的一 统计边/弧数 NFINITY的元素个数的一半 义 有向图: cacf1a时 有向图/网:图中表结点的数目 i=0j=0 有向网:G.arcs中adj值不为 INFINITY的元素个数 文档编号 完成时间 完成人张昱 修改时间20026-6 第4页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 4 页 2) 邻接表的头结点 typedef struct VNode{ VertexType data; /* 顶点信息 */ ArcNode *firstarc; /* 邻接表指针 */ }VNode, AdjList[MAX_VERTEX_NUM]; 3) 图的整体结构 typedef struct { AdjList vertices; int vexnum, arcnum; GraphKind kind; }ALGraph; 4、邻接矩阵与邻接表的对比 假设图为 G,顶点数为 n,边/弧数为 e。 A 邻接矩阵 B 邻接表 存储空间 O(n+n2 ) O(n+e) 图的创建算 法 T1(n)=O(e+n2 )或 T2(n)=O(e*n+n2 ) T1(n)=O(n+e)或 T2(n)=O(e*n) T1(n)是指在输入边/弧时,输入的顶点信息为顶点的编号;而 T2(n)则指 在输入边/弧时,输入的为顶点本身的信息,此时需要查找顶点在图中的 位置 无向图中求 第 i 顶点的度 G arcs i j adj n j . [ ][ ]. 1 0 − = (第 i 行之和)或 G arcs j i adj n j . [ ][ ]. 1 0 − = (第 i 列之和) G.vertices[i].firstarc 所指向的邻接 表包含的结点个数 无向网中求 第 i 顶点的度 第 i 行/列中 adj 值不为 INFINITY 的 元素个数 有向图中求 第i顶点的入/ 出度 入度: − = 1 0 . [ ][ ]. n j G arcs j i adj (第 i 列) 出度: − = 1 0 . [ ][ ]. n j G arcs i j adj (第 i 行) 入度:扫描各顶点的邻接表,统计 表结点的adjvex为i的表结点个数 T(n)=O(n+e) 出度:G.vertices[i].firstarc 所指向 的邻接表包含的结点个数 有 向网中求 第i顶点的入/ 出度 入度:第 i 列中 adj 值不为 INFINITY 的元素个数 出度:第 i 行中 adj 值不为 INFINITY 的元素个数 统计边/弧数 无向图: − = − = 1 0 1 0 . [ ][ ]. 2 1 n i n j G arcs i j adj ) 无向网: G.arcs 中 adj 值不为 INFINITY 的元素个数的一半 有向图: − = − = 1 0 1 0 . [ ][ ]. n i n j G arcs i j adj 有向网: G.arcs 中 adj 值不为 INFINITY 的元素个数 无向图/网:图中表结点数目的一 半 有向图/网:图中表结点的数目

教黎 第七章图 程序设计—数据结构 图的遍历算法及其应用 结论:邻接矩阵适于稠密图的存储,邻接表适于稀疏图的存储:邻接表求有向图的顶点的 入度不方便,要遍历各个顶点的邻接表。 7.2.2图的创建 基本过程: 1)输入图的类型,根据类型选择相应的创建算法 2)输入图的顶点数,边/弧数 3)输入并存储顶点信息 4)输入边/弧所关联的顶点对,将边或弧的信息存储到邻接矩阵/邻接表中 图的存储结构不同、图的类型不同,都会影响创建算法的实现细节:但是,图的总体创建 流程是一致的(如上)。 示例:用邻接矩阵表示法构造有向网G Status CreateMDG(MGraph &G){ /*步骤2:输入图的顶点数、边/弧数*/ scanf(&G.vexnum,&G.arcnum,&IncInfo;/体IncInfo为0则各弧不含其它信息*/ /*步骤3:输入并存储顶点信息 */ for (i=0:i<G.vexnum :++scanf (&G.vexsi]): /*步骤4:输入并存储边/弧信息 for(i=0;i<G.vexnum;i++) /体邻接矩阵初始化* for (j=0;j<G.vexnum ;j++) G.arcs[i][j]=(INFINITY,NULL); for(k=0;k <G.arcnum k++){ scanf (&v1,&v2,&w); i=LocateVex(G,v1);j=Locate Vex(G,v2); G.arcs[i][j].adj=w; if(Inclnfo)Input(*G.arcs]j].info);/体*G.arcs[i][].info要求G.arcs[]i[jl.info指向的 空间在调用Input()前分配*/ } 7.3图的遍历 7.3.1深度优先搜索 1、分析 ·类似于树的先序遍历 ·引入访问标志数组visit[0:n-1],区分顶点是否已被访问 ·非连通图,需引入多个深度优先搜索的起始顶点 ·递归算法或基于栈的非递归算法 2、基于ADT Graph的DFS算法 Boolean visited[MAX VERTEX NUM]; void DFSTraverse(Graph G,Status(*Visit )(Graph G,int v)) { for(v=0;v <G.vexnum;++v)visited[v]=FALSE; for(v=0;v<G.vexnum;++v) if(!visited[v]) DFS(G,v,Visit); } 文档编号 完成时间 完成人张昱 修改时间20026-6 第5页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 5 页 结论:邻接矩阵适于稠密图的存储,邻接表适于稀疏图的存储;邻接表求有向图的顶点的 入度不方便,要遍历各个顶点的邻接表。 7.2.2 图的创建 基本过程: 1)输入图的类型,根据类型选择相应的创建算法 2)输入图的顶点数,边/弧数 3)输入并存储顶点信息 4)输入边/弧所关联的顶点对,将边或弧的信息存储到邻接矩阵/邻接表中 图的存储结构不同、图的类型不同,都会影响创建算法的实现细节;但是,图的总体创建 流程是一致的(如上)。 示例:用邻接矩阵表示法构造有向网 G Status CreateMDG(MGraph &G){ /* 步骤 2:输入图的顶点数、边/弧数 */ scanf (&G.vexnum, &G.arcnum, &IncInfo); /* IncInfo 为 0 则各弧不含其它信息 */ /* 步骤 3:输入并存储顶点信息 */ for ( i=0; i<G.vexnum ; i++) scanf ( &G.vexs[i] ); /* 步骤 4:输入并存储边/弧信息 */ for ( i = 0; i < G.vexnum ; i++) /* 邻接矩阵初始化 */ for ( j = 0; j < G.vexnum ; j++) G.arcs[i][j] = {INFINITY, NULL}; for ( k = 0; k < G.arcnum ; k++){ scanf (&v1, &v2, &w); i = LocateVex(G, v1); j = LocateVex(G, v2); G.arcs[i][j].adj = w; if ( IncInfo) Input( *G.arcs[i][j].info); /* *G.arcs[i][j].info要求G.arcs[i][j].info指向的 空间在调用 Input()前分配 */ } } 7.3 图的遍历 7.3.1 深度优先搜索 1、分析 ·类似于树的先序遍历 ·引入访问标志数组 visit[0:n-1],区分顶点是否已被访问 ·非连通图,需引入多个深度优先搜索的起始顶点 ·递归算法或基于栈的非递归算法 2、基于 ADT Graph 的 DFS 算法 Boolean visited[MAX_VERTEX_NUM]; void DFSTraverse(Graph G, Status ( *Visit ) (Graph G, int v) ) { for ( v = 0; v < G.vexnum; ++v ) visited[v] = FALSE; for ( v = 0; v < G.vexnum; ++v ) if ( !visited[v] ) DFS(G, v, Visit); }

教黎 第七章图 程序设计—数据结构 图的遍历算法及其应用 void DFS(Graph G,int v,Status (*Visit )(Graph G,int v)) { visited[v]=TRUE;Visit(G,v); for w=FirstAdjVex(G,v);w;w=NextAdjVex(G,v,w)) if(!visited[w])DFS(G,w,Visit); } 3、基于某种存储结构的DFS算法 根据选择的存储结构,决定FirstAdjVex()和NextAdjVex()的实现,重新整合算法。 如采用邻接矩阵表示法表示的图,则DFS算法如下: void DFS(MGraph G,int v,Status(*Visit )(MGraph G,int v)) visited[v]=TRUE;Visit(G,v); for w=0;wnextarc) if(!visited[p->adjvex])DFS(G,p->adjvex,Visit); 7.3.2广度优先搜索 1、分析 ·类似于树的层次遍历 ·引入visited访问标志数组 ·非连通图,需引入多个广度优先搜索的起始顶点 ·引入队列保存“顶点已访问,但其邻接点未全访问”的顶点编号 2、基于ADT Graph的BFS算法 void BFSTraverse(Graph G,Status(*Visit)(Graph G,int v)) for(v=0;v<G.vexnum;++v visited[v]=FALSE; InitQueue(Q); for (v=0;v<G.vexnum;++v if(!visited[v]) /*访问某连通分量的起始顶点,起点入队*/ visited[v]=TRUE;Visit(G,v); EnQueue(Q,v); while(!QueueEmpty(Q)){ 体出队,访问出队元素的邻接点* DeQueue(Q.u): for w=FirstAdiVex(G.u):w:w=NextAdiVex(G.u.w)) if(Ivisited[w]) 体访问顶点u的尚未访问的邻接点并入队*/ visited[w]=TRUE;Visit(G,w); EnQueue(Q,w); 文档编号 完成时间 完成人张昱 修改时间20026-6 第6页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 6 页 void DFS(Graph G, int v, Status ( *Visit ) (Graph G, int v) ) { visited[v] = TRUE; Visit(G, v); for ( w = FirstAdjVex(G, v); w; w = NextAdjVex(G, v, w) ) if ( !visited[w] ) DFS(G, w, Visit); } 3、基于某种存储结构的 DFS 算法 根据选择的存储结构,决定 FirstAdjVex()和 NextAdjVex()的实现,重新整合算法。 如采用邻接矩阵表示法表示的图,则 DFS 算法如下: void DFS (MGraph G, int v, Status ( *Visit ) (MGraph G, int v)) { visited[v] = TRUE; Visit(G, v); for ( w = 0; w nextarc) if (!visited[p->adjvex] ) DFS(G, p->adjvex, Visit); } 7.3.2 广度优先搜索 1、分析 ·类似于树的层次遍历 ·引入 visited 访问标志数组 ·非连通图,需引入多个广度优先搜索的起始顶点 ·引入队列保存“顶点已访问,但其邻接点未全访问”的顶点编号 2、基于 ADT Graph 的 BFS 算法 void BFSTraverse (Graph G, Status ( *Visit ) (Graph G, int v) ) { for ( v = 0; v < G.vexnum; ++v ) visited[v] = FALSE; InitQueue (Q); for ( v = 0; v < G.vexnum; ++v ) if ( !visited[v] ){ /* 访问某连通分量的起始顶点,起点入队 */ visited[v] = TRUE; Visit(G, v); EnQueue(Q, v); while( !QueueEmpty(Q) ){ /* 出队,访问出队元素的邻接点 */ DeQueue(Q,u); for ( w = FirstAdjVex( G, u) ; w ; w = NextAdjVex(G, u, w) ) if ( !visited[w] ){ /* 访问顶点 u 的尚未访问的邻接点并入队 */ visited[w] = TRUE; Visit(G, w); EnQueue(Q, w); }

敦案 第七章图 程序设计—数据结构 图的遍历算法及其应用 } 3、基于某种存储结构的BFS算法 如采用邻接矩阵表示法表示的网,则算法如下: void BFSTraverse(MGraph G,Status(*Visit )(MGraph G,int v)) for (v=0;vnextarc) if (!visited[p->adjvex]){ 体访问顶点u的尚未访问的邻接点并入队*/ visited[p->adjvex]=TRUE;Visit(G,p->adjvex); EnQueue(Q,p->adjvex); 文档编号 完成时间 完成人张昱 修改时间20026-6 第7页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 7 页 } } } 3、基于某种存储结构的 BFS 算法 如采用邻接矩阵表示法表示的网,则算法如下: void BFSTraverse(MGraph G, Status ( *Visit ) (MGraph G, int v) ) { for ( v = 0; v nextarc ) if ( !visited[p->adjvex] ){ /* 访问顶点 u 的尚未访问的邻接点并入队 */ visited[p->adjvex] = TRUE; Visit(G, p->adjvex); EnQueue(Q, p->adjvex); } } } }

敦案 第七章图 程序设计—数据结构 图的遍历算法及其应用 7.4遍历算法的应用 7.4.1应用问题概述 图的深度优先遍历: 1、求一条包含图中所有顶点的简单路径(简单回路) 2、判断图中是否存在环 3、求图中通过给定顶点Vk的简单回路 4、判断是否存在从顶点到顶点的路径 5、判别v0和v1之间是否存在一条长度为k的路径 图的广度优先遍历: 1、判断是否存在从顶点到顶点的路径 2、求距V0的各顶点中最短路径长度最长的一个顶点。 3、求v0和v1之间的最短路径 4、在顶点子集U中找出距离顶点v0最近的顶点 5、求顶点v0到其余每个顶点的最短路径 6、求距离顶点v0的最短路径长度为k的所有顶点 7.4.2求一条包含图中所有顶点的简单路径 1、思路 对于任意的有向图或无向图G,并不一定都能找到符合题意的简单路径。这样的简单路径 要求包含G.vexnum个顶点,且互不相同。它的查找可以基于深度优先遍历。 在一个存在包含全部顶点的简单路径的图中,以下因素会影响该简单路径是否能顺利地查 到: l)起点的选择:如图(a),其符合题意的一条简单 路径如图(b)。若起点为1,则不能找到符合题 ④ 意的简单路径: 7 2)顶点的邻接点次序:进一步考察图(a),即使以 (6 2为起点,但是2的邻接点选择的是1,而不是 (a) (b) 5,此时也不能找到符合题意的解。 在基于DFS的查找算法中,由于起点和邻接点的选取是与顶点和邻接点的存储次序以及算 法的搜索次序有关,不可能依据特定的图给出特定的解决算法。因此,在整个搜索中应允许有 查找失败,此时可采取回湖到上一层的方法,继续查找其他路径。 文档编号 完成时间 完成人张昱 修改时间20026-6 第8页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 8 页 7.4 遍历算法的应用 7.4.1 应用问题概述 图的深度优先遍历: 1、 求一条包含图中所有顶点的简单路径(简单回路) 2、 判断图中是否存在环 3、 求图中通过给定顶点 vk的简单回路 4、 判断是否存在从顶点 vi到顶点 vj的路径 5、 判别 v0 和 v1 之间是否存在一条长度为 k 的路径 图的广度优先遍历: 1、 判断是否存在从顶点 vi到顶点 vj的路径 2、 求距 v0 的各顶点中最短路径长度最长的一个顶点。 3、 求 v0 和 v1 之间的最短路径. 4、 在顶点子集 U 中找出距离顶点 v0 最近的顶点 5、 求顶点 v0 到其余每个顶点的最短路径 6、 求距离顶点 v0 的最短路径长度为 k 的所有顶点 7.4.2 求一条包含图中所有顶点的简单路径 1、思路 对于任意的有向图或无向图 G,并不一定都能找到符合题意的简单路径。这样的简单路径 要求包含 G.vexnum 个顶点,且互不相同。它的查找可以基于深度优先遍历。 在一个存在包含全部顶点的简单路径的图中,以下因素会影响该简单路径是否能顺利地查 到: 1)起点的选择:如图(a),其符合题意的一条简单 路径如图(b)。若起点为 1,则不能找到符合题 意的简单路径; 2)顶点的邻接点次序:进一步考察图(a),即使以 2 为起点,但是 2 的邻接点选择的是 1,而不是 5,此时也不能找到符合题意的解。 在基于 DFS 的查找算法中,由于起点和邻接点的选取是与顶点和邻接点的存储次序以及算 法的搜索次序有关,不可能依据特定的图给出特定的解决算法。因此,在整个搜索中应允许有 查找失败,此时可采取回溯到上一层的方法,继续查找其他路径。 1 2 3 4 5 6 7 1 2 3 4 5 6 7 (a) (b)

教黎 第七章图 程序设计—数据结构 图的遍历算法及其应用 这样,引入数组Ph用来保存当前已搜索的简单路径上的顶点,引入计数器n用来记录 当前该路径上的顶点数。 对DFS算法的修改如下: 1)计数器n的初始化,放在visited的初始化前后: 2)访问顶点时,增加将该顶点序号入数组Path中,计数器nt+:判断是否已获得所求路 径,是则输出结束,否则继续遍历邻接点: 3)某顶点的全部邻接点都访问后,仍未得到简单路径,则回溯,将该顶点置为未访问, 计数器n-一。 2、算法 /体邻接矩阵表示法,粗体字部分为在深度优先遍历上的增加或修改的步骤*/ void Hamilton(MGraph G) for (i=0;i<G.vexnum;i++) visited[i]=FALSE: n=0; for i=0;i<G.vexnum;+) if(!visited[i]DFS(G,i); void DFS(MGraph G,int i) visitedfi]=TRUE: Path[n]=i; n++; if(n=G.vexnum)Print(Path);/体符合条件,输出该简单路径*/ for(j=0;j<G.vexnum;j++) if(G.arcs[i][j].adj&&!visited[j]) DFS(G,j)月 visited[i]FALSE; n--; } 3、思考 1)若图中存在多条符合条件的路径,本算法是输出一条,还是输出全部? 2)如何修改算法,变成判断是否有包含全部顶点的简单路径? 3)如何修改算法,输出包含全部顶点的简单路径的条数? 4)如何修改算法,输出所有的简单回路? 5)考虑其他图的存储方法对算法的影响: 6)考虑在非递归的深度优先遍历算法上,如何修改使之适应本问题的求解。 7.4.3求距v0的各顶点中最短路径长度最长的一个顶点 1、思路 由于题意强调为最短路径,因此应当考虑BFS的算法应用。本问题的求解转变成:从vO 出发进行BFS,最后一层的顶点距离vO的最短路径长度最长。 由于BF$类似于树的按层次遍历,需要引入队列用来保存本身已访问但其邻接点尚未全部 访问的顶点。BFS遍历中最后一层的顶点一定是最后出队的若干顶点,队列中最后一个出队的 顶点必定是符合题意的顶点。 这样,只需调用BFS的算法,将最后出队的元素返回即可。 2、算法 文档编号 完成时间 完成人张昱 修改时间20026-6 第9页
程序设计——数据结构 第七章 图 图的遍历算法及其应用 文档编号 完 成 人 张 昱 完成时间 修改时间 2002-6-6 第 9 页 这样,引入数组 Path 用来保存当前已搜索的简单路径上的顶点,引入计数器 n 用来记录 当前该路径上的顶点数。 对 DFS 算法的修改如下: 1)计数器 n 的初始化,放在 visited 的初始化前后; 2)访问顶点时,增加将该顶点序号入数组 Path 中,计数器 n++;判断是否已获得所求路 径,是则输出结束,否则继续遍历邻接点; 3)某顶点的全部邻接点都访问后,仍未得到简单路径,则回溯,将该顶点置为未访问, 计数器 n--。 2、算法 /* 邻接矩阵表示法, 粗体字部分为在深度优先遍历上的增加或修改的步骤 */ void Hamilton(MGraph G) { for ( i=0; i<G.vexnum; i++ ) visited[i] = FALSE; n = 0; for ( i=0; i<G.vexnum; i++ ) if ( !visited[i] ) DFS (G, i); } void DFS(MGraph G, int i) { visited[i] = TRUE; Path[n] = i; n++; if ( n == G.vexnum ) Print(Path); /* 符合条件,输出该简单路径 */ for( j=0; j<G.vexnum; j++ ) if ( G.arcs[i][j].adj && !visited[j]) DFS( G, j ); visited[i] = FALSE; n--; } 3、思考 1)若图中存在多条符合条件的路径,本算法是输出一条,还是输出全部? 2)如何修改算法,变成判断是否有包含全部顶点的简单路径? 3)如何修改算法,输出包含全部顶点的简单路径的条数? 4)如何修改算法,输出所有的简单回路? 5)考虑其他图的存储方法对算法的影响; 6)考虑在非递归的深度优先遍历算法上,如何修改使之适应本问题的求解。 7.4.3 求距 v0 的各顶点中最短路径长度最长的一个顶点 1、思路 由于题意强调为最短路径,因此应当考虑 BFS 的算法应用。本问题的求解转变成:从 v0 出发进行 BFS,最后一层的顶点距离 v0 的最短路径长度最长。 由于 BFS 类似于树的按层次遍历,需要引入队列用来保存本身已访问但其邻接点尚未全部 访问的顶点。BFS 遍历中最后一层的顶点一定是最后出队的若干顶点,队列中最后一个出队的 顶点必定是符合题意的顶点。 这样,只需调用 BFS 的算法,将最后出队的元素返回即可。 2、算法