
数据结构 图 第七章图 主讲:张昱 重点:图在邻接矩阵和邻接表上的遍历算法 yuzhang@ustc.edu (DFS,BFS)及其应用 0551-3603804 难点:求图的最小生成树、最短路径、拓扑排 序、关键路径等算法及其应用、性能分析 1/106 2/106 第七章图 上7.1图的定义和术语(1) 7.1图的定义和术语 ■图的定义 7.2图的存储结构 ,图是由项点集合(vertex)及顶点之间的关系集 佥组成的一种数据结构。 7.3图的遗历 记为G=(口,{E)顶点集,E关系的集合 7.4图的连通性问题 ,顶点之间的关系是多对多的(m:) 7.5有向无环图及其应用 ,顶点之间的关系是否有方向性: 有向图、无向图 7.6最短路径 3/106 4/106 图 7.1图的定义和术语(2) 17.1图的定义和术语(2) ,无向图 ,有向图 ,边(,w)€E(g,wE),与w互为接点,边(%w座 ,顶点v的入度是以¥为薰头的孤的数国,记为D(归 胜于顶点和w,减者说边(w)和顶点以,相关联。 v的出度是以v为薰尾的蕴的数司,记为OD(吵防 ,顶点v的度是和相关联的边的数目,记为TD(), v的度是TD()=D()+OD(. 。有向图 ■路径与连通性 ,弧∈E(,w∈,w为燕头为蕴L:顶燕v绝 路径、简单路径、回路环)、简单回路 接到顶越w,顶燕w邻接自顶点,孤和顶项点 ,相关联。 顶,点之门的连通性、无向连通困、有向强连通困 5/106 图 6/106 图
1/106 数据结构——图 主讲:张昱 yuzhang@ustc.edu 0551-3603804 2/106 重点:图在邻接矩阵和邻接表上的遍历算法 (DFS, BFS)及其应用 难点:求图的最小生成树、最短路径、拓扑排 序、关键路径等算法及其应用、性能分析 第七章 图 3/106 第七章 图 7.1 图的定义和术语 7.2 图的存储结构 7.3 图的遍历 7.4 图的连通性问题 7.5 有向无环图及其应用 7.6 最短路径 4/106 7.1 图的定义和术语(1) 图的定义 图是由顶点集合(vertex)及顶点之间的关系集 合组成的一种数据结构。 记为G = (V, {E}) V-顶点集,E-关系的集合 顶点之间的关系是多对多的(m : n) 顶点之间的关系是否有方向性: 有向图、无向图 5/106 7.1 图的定义和术语(2) 无向图 边(v,w) ∊ E (v,w ∊V),v与w互为邻接点,边( v, w )依 附于顶点v和w,或者说边( v, w )和顶点v, w相关联。 顶点v 的度是和v相关联的边的数目,记为TD(v) 。 有向图 弧 ∊ E (v,w ∊V),w为弧头, v为弧尾; 顶点v 邻 接到顶点w,顶点w 邻接自顶点v,弧和顶点 v、w相关联。 6/106 7.1 图的定义和术语(2) 有向图 顶点v 的入度是以v 为弧头的弧的数目,记为ID(v); v 的出度是以v为弧尾的弧的数目,记为OD(v); v 的度是TD(v) = ID(v) + OD(v)。 路径与连通性 路径、简单路径、回路(环)、简单回路 顶点之间的连通性、无向连通图、有向强连通图

7.1图的定义和术语(3) 7.1图的定义和术语(4) ,对于有向图G ,对于无向图G ,VVV:VV,是从V,到V,的路径,不是简单路径; ,V VVV.V2是V,和V,间的路径,但不是简单路径; ,VV,是简单路径: ,VV,是简单路径; ▣VV,V:VV3VV是环,不是简单环; G ,V2VVV2VV,V是环,但不是简单环 ·VVV,V是简单环. V2VgVV是简单环。 .ID(V)-1.OD(V)-2,TD(V)-3 ■TDV,-2 ·Y柔V是连通的:从V,到,是连通的,⑦ ⊙ ,V和V,是连通的 但从V到V,是不连通的. ,G,是连通图 ,G不是强连通图 71106 回 8/106 图 7.1图的定义和术语(5) 7.1图的定义和术语(6) ·子图、连通性 ·对于G=(V,{E),它的子图 G ·子图、连通性 G满足: B ·生成树极小连通子图 A 1)V'S V; ,极大、极小是就边数的多少 ©⑩E 2)E'S E: @ 而言的 3)G'-(V”,{E9) o@① ,连通分量极大连通子图 ①①® ①①⑧ ,强连通分量一有向国中的板心 大强连通子图 连通分量 生成树 9/106 图 10/106 图 71图的定义和术酒(7) 71图的定义和术语(8) ■边/弧数目 ·边/弧数目 用n表示图中顶点数目,用e表示田中边戒孤的数目 思考:若无向图中有21条边,则: 。无向国:0≤e≤h(m-1) 1)保特斌图不连通至少应具有多少个顶点? 完全因e=以(m-l) 2)保特斌图连通玉少有多少个项点,玉多有多少个项 ,有向因:0≤e≤m-) 有向完全图e=n(n-I) 点? ,希城困:e<nlogn 1)m个顶点形成完全困,另一个顶燕与这m个顶点不 斜密因 连 。若困中边或孤上有权,则该困称为网 ⅓m(m-1)-21m-7之-mt1-8 2)至少有7个顶点(完全困),至多有22个顶点(生成树) 有向因、有向网、无向园、无向网 图 12/106
7/106 7.1 图的定义和术语(3) 对于有向图G1 V1V3V4V1V2 是从V1 到V2 的路径, 不是简单路径; V1V2是简单路径; V1V3V4V1V3V4V1是环,不是简单环; V1V3V4V1是简单环。 ID(V1)=1, OD(V1)=2, TD(V1)=3 V1和V4是连通的;从V1到V2是连通的, 但从V2到V1是不连通的。 G1不是强连通图 V1 V3 V2 V4 G1 8/106 7.1 图的定义和术语(4) 对于无向图G2 V1V2V3V5V2 是V1和V2间的路径,但不是简单路径; V1V2是简单路径; V2V3V5V2V3V5V2是环,但不是简单环 V2V3V5V2是简单环。 TD(V1)=2 V1和V4是连通的 G2是连通图 V1 V2 V3 V4 V5 G2 9/106 7.1 图的定义和术语(5) 子图、连通性 对于G=(V, {E}),它的子图 G'满足: 1) V'⊆ V; 2) E'⊆ E; 3) G'=(V', {E'}) 连通分量—极大连通子图 强连通分量—有向图中的极 大强连通子图 G3 D E I G H K A C B F L J M A C B F L J M I G H K 连通分量 10/106 7.1 图的定义和术语(6) 子图、连通性 生成树—极小连通子图 极大、极小是就边数的多少 而言的 G3 D E I G H K A C B F L J M A C B F L J M I G H K 生成树 11/106 7.1 图的定义和术语(7) 边/弧数目 用n 表示图中顶点数目,用e 表示图中边或弧的数目 无向图:0 ≤ e ≤ ½ n(n-1) 完全图 e = ½ n(n-1) 有向图:0 ≤ e ≤ n(n-1) 有向完全图 e = n(n-1) 稀疏图: e < nlogn 稠密图 若图中边或弧上有权,则该图称为网 有向图、有向网、无向图、无向网 12/106 7.1 图的定义和术语(8) 边/弧数目 思考:若无向图中有21条边,则: 1) 保持该图不连通至少应具有多少个顶点? 2) 保持该图连通至少有多少个顶点,至多有多少个顶 点? 1) m个顶点形成完全图,另一个顶点与这m个顶点不 连通 ½ m(m-1)=21 Î m=7 Î n=m+1=8 2) 至少有 7 个顶点(完全图),至多有22个顶点(生成树)

敌据关系R:: 17.1图的定义-ADT Graph R=IVRI R=w水weV且P,w,w表示从v到w的到,谓词 P(vw) 定义了弧w的意义或信息制 ■ADT Graph 基本操作,。 ,查找:LocateVex(G,u) G”物米的项点集课是国中的集合 GetVex(G,v) 操作结果,按V和VR的定义构造图G FirstAdjVex(G,v) DestroyGrapl(&G) NextAdjVex(G,v,w) 初始杀件:图G存在 ■插入:InsertVex(&G,v) 操作结果:销毁图G LocateVex(G n) InsertArc(&G,v,w) 初始杀件:图G已存在,a和G中项点有相同特征 ,副除:DeleteVex(&G,v) 操作结果:若G中存在项点山,返回该项点在图中位置。否则返 DeleteArc(&G,v,w) 回其它信 ,通历:DFSTraverse(G,v,Visit() GetVex(G v) 初始条件:图G存在,v是G中某个顶点 BFSTraverse(G,v,Visit()) 回 作结来:返回v的值 13/106 14/106 图 PutVex(&G v,value) 初始条件:图G存在,v是G中某个顶点 InsertAre&G.v.w) 初始条件:图G存在,v和W是G中两个页点 操作结果:对v赋值vae 操作结果:在图G中增添到w>,若G是无向的,则还应增添对 初始条件:图G存在,v是G中某个顶点 称w,v DeleteArc(&G.v.w) 操作结果:返回v的第一个邻接项点。若顶点在G中设有邻接项点, 初始条件:图G存在,v和w是G中两个页点 则返回“空” 操作结果:别除G中的买w,若G是无向的,则还应副除对称 NextAdiVex(G vw 初暗亲作,图G存在,v是G中某个项点,w是v的邻接顶点 DESTraverse(G v,visit 操作结果:返回v的(相对于w的下一个邻接顶点。若w是v的最 初始件:图G存在,v是G中某个顶点,s城是对面点的应用函 后一个邻接点,则返回“空”。 数 InsertVex(&G v) 作结果:从点起深度优先滴历图G,并对每个点调用函裁 初始条件:图G存在,v和G中顶点有相同特征 it一次且至多一次。一且i()失败,刚操作失收 操作结果,在图中增添新项点 BFSTraverse(G v,visit( 初黯条件:图G存在,v是G中某个顶点,是对面点的应用函 DeleteVex(&G v) 初始条件:图G存在,v是G中某个顶点 搡作结果:从顾点v起广度优先遍历图G,并对每个顶点调用函数 操作结果:删除G中顶点¥及其相关的弧 it)一次且至多一次.一旦i此)失敞,操作失收 圆 ADT Graph 15/106 16/106 图 7.2图的存储结构(1) 生72图的存储结构(2) 。图的存储表示分析 ■图的存储表示分析 。特点:顶点之间的关系是多对多(m:) ,”m和n都是不定的,无法进行非战性结构的战性化 ,顶点集的存储 “,图中的关系不能通过顺序映像(即通过顶点之间的存 用顺序表存储,不是顺序映像! 储位置反映顶点之间的辽辉关系)反映;必须另外引入 。关系集的存储 存储空间反映顶点之间的怀接关系。 邻接矩阵、邻接表、多重邻接表、十字链表 。图的存储信息 顶燕信惠、边/孤信息 燮体信息:顶点数、边/蕴散、图的种类(有向图/有向 网/无向因/无向网) 17/106 图 18/106 回
13/106 7.1 图的定义-ADT Graph ADT Graph 查找:LocateVex(G, u) GetVex(G, v) FirstAdjVex(G, v) NextAdjVex(G, v, w) 插入:InsertVex(&G, v) InsertArc(&G, v, w) 删除:DeleteVex(&G, v) DeleteArc(&G, v, w) 遍历:DFSTraverse(G, v, Visit()) BFSTraverse(G, v, Visit()) 14/106 15/106 16/106 17/106 7.2 图的存储结构(1) 图的存储表示分析 特点:顶点之间的关系是多对多(m : n) ∵m 和 n 都是不定的,无法进行非线性结构的线性化 ∴图中的关系不能通过顺序映像(即通过顶点之间的存 储位置反映顶点之间的逻辑关系)反映;必须另外引入 存储空间反映顶点之间的邻接关系。 图的存储信息 顶点信息、边/弧信息 整体信息:顶点数、边/弧数、图的种类(有向图/有向 网/无向图/无向网) 18/106 7.2 图的存储结构(2) 图的存储表示分析 顶点集的存储 用顺序表存储,不是顺序映像! 关系集的存储 邻接矩阵、邻接表、多重邻接表、十字链表
17.2图的存储结构-邻接矩阵 7.2图的存储结构-邻接矩阵 ■数组表示法—邻接矩阵 ■数组表示法 邻接矩阵 #define INFINITY INT MAX typedef structf typedef enum(DG,DN,AG.AN)GraphKind: typedef struct ArcCellf ∥顶点向量 ∥顶点间的关系,无权图:0-不相邻,1-相邻 VertexType vexs[MAX_VERTEX_NUM]; ∥有权图:权值,NFINITY-不相怀 ∥关系果 int adj; AdiMatrix arcs; InfoType *info:∥这航相关信息的指针 int vexnum,arcnum;∥项,点数、边/孤数 AreCell. GraphKind kind; ∥困的种类 AdjMatrix|MAX_VERTEX_NUMIIMAX_VERTEX_NUM]: }MGraph; 19/106 回 20/106 图 7.2图的存储结构-邻接矩阵 」7.2图的存储结构-邻接矩阵 ,无向图一对称矩阵 ,有向图—未必是对称矩阵 无权图:邻接矩阵中的元素为0-不邻接; 邻接矩阵中的元素为1-邻接 G VI的 11 V1的度, 01010 出度 0000 0101 0001 值为1日 0 000 元素个 00 V1的 1100 入度 2L/106 图 22/106 图 尘7.2图的存储结构邻装矩阵 尘上72图的存储结构餐装款 。有向网一未必是对称矩阵(图7.9,P162) ·邻接表 网:权值-邻接;极限值-不邻接 无向图/网:边表,表结点的个数为边数的两倍 G 有白田/网:出边表,表结点的个数为孤数 oo 5 0o 7 oo 0o typedef struct AreNode{∥表结,点 的出 09 int adjvex;:∥弧所指向的顶点的位置 0006 struct AreNode*nextarc;/∥指向下一条孤的指针 5 InfoType *info; ArcNode; 23/106 图 24/106 图
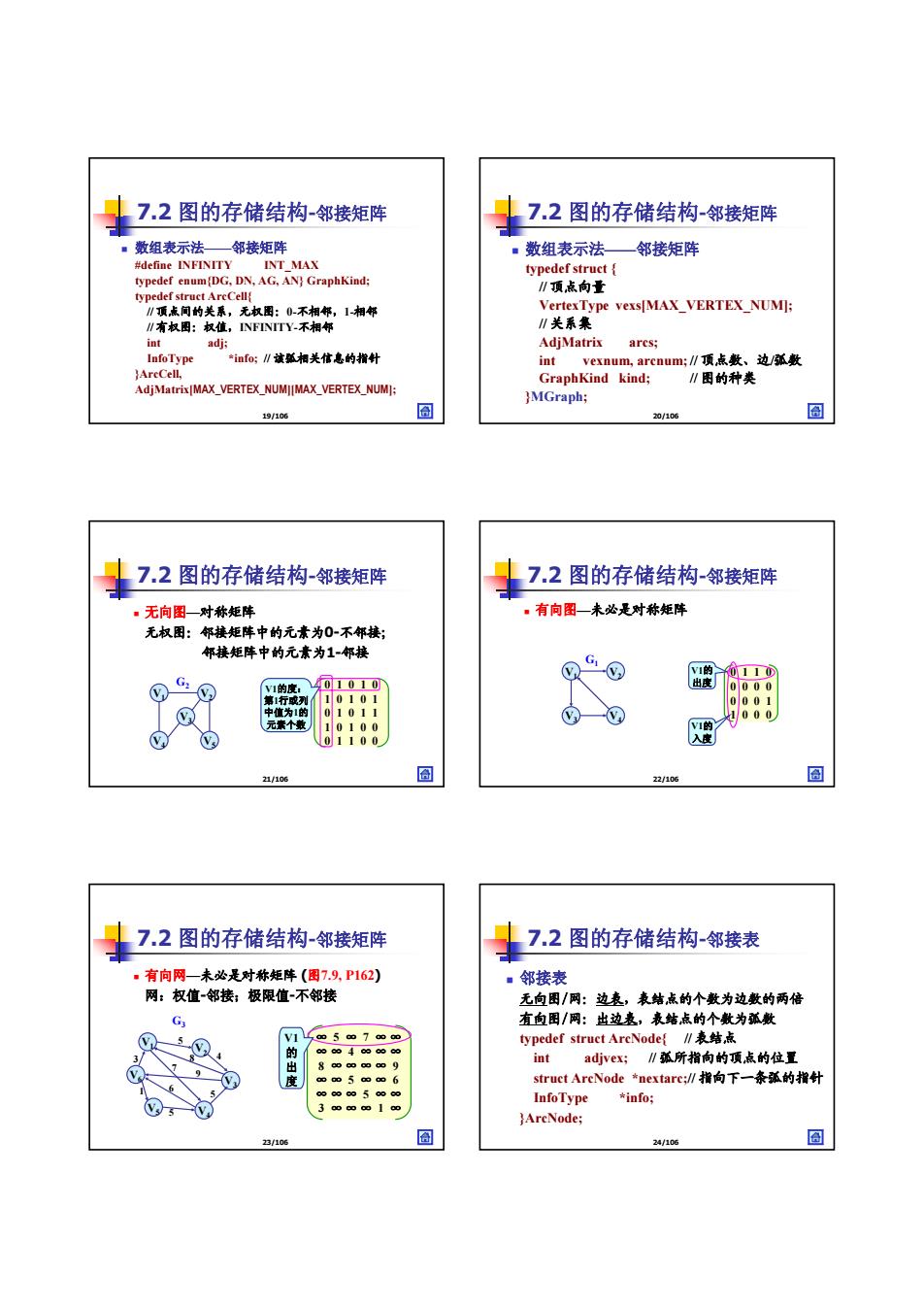
19/106 7.2 图的存储结构-邻接矩阵 数组表示法——邻接矩阵 #define INFINITY INT_MAX typedef enum{DG, DN, AG, AN} GraphKind; typedef struct ArcCell{ // 顶点间的关系,无权图:0-不相邻,1-相邻 // 有权图:权值,INFINITY-不相邻 int adj; InfoType *info; // 该弧相关信息的指针 }ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; 20/106 7.2 图的存储结构-邻接矩阵 数组表示法——邻接矩阵 typedef struct { // 顶点向量 VertexType vexs[MAX_VERTEX_NUM]; // 关系集 AdjMatrix arcs; int vexnum, arcnum;// 顶点数、边/弧数 GraphKind kind; // 图的种类 }MGraph; 21/106 7.2 图的存储结构-邻接矩阵 无向图—对称矩阵 无权图:邻接矩阵中的元素为0-不邻接; 邻接矩阵中的元素为1-邻接 V1 V2 V3 V4 V5 G2 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 V1的度: 第1行或列 中值为1的 元素个数 22/106 7.2 图的存储结构-邻接矩阵 有向图—未必是对称矩阵 V1 V3 V2 V4 G1 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 V1的 出度 V1的 入度 23/106 7.2 图的存储结构-邻接矩阵 有向网—未必是对称矩阵 (图7.9, P162) 网:权值-邻接;极限值-不邻接 V1 V2 V3 V5 V6 G3 5 8 4 3 V4 9 7 6 1 5 5 ∞ 5 ∞ 7 ∞ ∞ ∞ ∞ 4 ∞∞∞ 8 ∞∞∞∞ 9 ∞ ∞ 5 ∞ ∞ 6 ∞∞∞ 5 ∞ ∞ 3 ∞∞∞ 1 ∞ V1 的 出 度 24/106 7.2 图的存储结构-邻接表 邻接表 无向图/网:边表,表结点的个数为边数的两倍 有向图/网:出边表,表结点的个数为弧数 typedef struct ArcNode{ // 表结点 int adjvex; // 弧所指向的顶点的位置 struct ArcNode *nextarc;// 指向下一条弧的指针 InfoType *info; }ArcNode;

17.2图的存储结构-邻接表 上7.2图的存储结构-邻接表 。邻接表 ·无向图/网一边表 typedef struct VNodef ∥头结点 注意:表结,点存放的是顶底在顶点顺序表中的偏号,不 VertexType data; ∥顶点信惠 是顶燕的基本信息。 ArcNode *firstare;:∥邻接表指针 V,的度 }VNode,AdjList[MAX VERTEX NUM]; o V, 3 typedef struct{ 1 V2 423 0 AdiList vertices; 2 4 31 int vexnum,arenum;∥项,点数、边/孤数 3 2 0 GraphKind kind; ∥困的种类 21 ALGraph; 25/106 回 26/106 图 7.2图的存储结构邻接表 士7.2图的存储结构-一图的创建 ,有向图/网一出边表 图的创建算法 。输入图的类型,根据类型选择相应的创建算法 0V231 。输入图的顶点数,边/弧数 IV^ V,的出度 3 ·输入并存储顶点信息 0 ·输入边/弧所关联的顶点对,将边或弧的信息存储到邻 V,的入度 师接表一出边表 接矩阵/邻接表中 , 3 教材中的算法7.1-7.3 1 0 图的存储结构不同、图的类型不同,都会形响创建算法 0 的实现细节;但是,图的总体创建流混是一致的1 2 ·邻接短阵与邻接表的对比 逆你接表一入边表 27/10 28/106 图 假设图为G,顷点数为m,边弧数为c。 邻接矩阵 邻接表 邻接垣阵 邻接表 存储空间。 0a+n2 O(nte TI(n-0(c+T2(n)-0(e'n+p2) T1m=0ate或T2a=0cn 有自图中求 入度: 图的创建算T1仙是指在输入边孤时,输入的顺点信总为项点的第号:而T2侧则指 0arc刑4第列 入度:扫描各顶点的邻接表,统计 在箱输入边孤时,输入的为顶点本身的信息,此时需要查找顶点在图中的 第顶点的入 位置: 出度 出底总Grf时第1m 表结点的ar为的表结点个数 T(n)=O(nte) 无向图中求 分cacf利[a4(第行之和或 有向时中求 入废:第i列中a值不为NFINITY 出度:Gvertices]firstare所指向 第顶点的度 总aaca第i收r Gvces.firstare所指向的邻接 第顶点的入 的元素个数, 的邻接表包含的结点个数: 表包含的结点个数。 出度 出度:第i行中a值不为NNT 无向网中求第i行例中ad值不为NFINITY的 的元素个数 第顶点的度元素个数 29106 30/106 图
25/106 7.2 图的存储结构-邻接表 邻接表 typedef struct VNode{ // 头结点 VertexType data; // 顶点信息 ArcNode *firstarc;// 邻接表指针 }VNode, AdjList[MAX_VERTEX_NUM]; typedef struct { AdjList vertices; int vexnum, arcnum;// 顶点数、边/弧数 GraphKind kind; // 图的种类 }ALGraph; 26/106 7.2 图的存储结构-邻接表 无向图/网—边表 注意:表结点存放的是顶点在顶点顺序表中的编号,不 是顶点的基本信息。 V1 V2 V3 V4 V5 G2 V1 V2 V3 V4 V5 0 1 2 3 4 3 1 ^ 4 2 2 0 ^ 4 3 1 ^ 0 ^ 2 1 ^ V1的度 27/106 7.2 图的存储结构-邻接表 有向图/网—出边表 V1 V3 V2 V4 G1 V1 V2 ^ V3 V4 0 1 2 3 2 1 ^ 0 ^ 3 ^ 邻接表—出边表 V1 V2 V3 V4 0 1 2 3 3 ^ 0 ^ 2 ^ 0 ^ 逆邻接表—入边表 V1的出度 V1的入度 28/106 7.2 图的存储结构—图的创建 图的创建算法 输入图的类型,根据类型选择相应的创建算法 输入图的顶点数,边/弧数 输入并存储顶点信息 输入边/弧所关联的顶点对,将边或弧的信息存储到邻 接矩阵/邻接表中 教材中的算法7.1~7.3 图的存储结构不同、图的类型不同,都会影响创建算法 的实现细节;但是,图的总体创建流程是一致的! 邻接矩阵与邻接表的对比 29/106 30/106

邻接矩阵 邻接表 7.2图的存储结构-十字链表 无,艺cc1 2局同 。十字链表一有向图(P165) 无向网:G心s中值不为无向图网:图中表结点数目的 ,有向图 。邻接表-出边表,求入度不方便 统计边孤数 NFINITY的元货个数的一半, 有商器:我Gar1 。逆邻接表-入边表 有向图网:图中表结点的数目, ,十字纯表域瓢被孤的 弧尾相同的弧的能城 00 有向网:Gcs中值不为 弧站燕 NFINITY的元素个数 tailvexhead小a=rnrc 被顶店被顶点的幕一条出薰 结论:邻接矩阵适于密图的存情,邻接表适于等说图的存储: 项点结点 邻接表求有向图的项点的入度不方便,要追历各个顶点的接表。, data firstin firstout 31/106 回 32/106 图 7.2图的存储结构-十字链表 ■十字链表一有向图 2阳的在储结构-+字链我 ·十字链表一有向图 #define MAX_VERTEX_NUM 20 顶,点结点 typedef struct VexNodef ∥孤结,点 VertexType data; typedef struct ArcBox{ ArcBox *firstin,*firstout; int tailvex,headvex; VexNode: ∥十字链表 struct ArcBox *hlink,*tlink; typedef struct InfoType *info; VexNode xlist[MAX_VERTEX_NUM]: ArcBox; int vexnum,arcnum; 33/106 图 OLGraph; 图 7.2图的存储结构-邻接多重表 」7.2图的存储结构邻接多重表 邻接多重表一无向图(P166) 邻接多重表一无向图 ·无向图 #define MAX VERTEX NUM 20 。邻接表-每” 该边 指向下一条依附于 typedef enum {unvisited,visited)VisitIf; ·多重邻排 顶点ivex的边 ∥边结点 标 填原丁 边蛙 typedef struct EBox{ mark ivex ilink ivex linLlinto VisitIf mark; 第一条依附于顶点的边 int ivex,jvex; 顶点结点 struct EBox *ilink,*jlink; InfoType *info; data firstedge }EBox; 5/1oe 图 36/106 画
31/106 32/106 7.2 图的存储结构-十字链表 十字链表—有向图 (P165) 有向图 邻接表-出边表,求入度不方便 逆邻接表-入边表 十字链表— 弧结点数==弧数 tailvex headvex hlink tlink info 弧结点 顶点结点 data firstin firstout 该弧的尾顶点的位置 该弧的头顶点的位置 弧头相同的弧的链域 弧尾相同的弧的链域 该顶点的第一条入弧 该顶点的第一条出弧 33/106 7.2 图的存储结构-十字链表 十字链表—有向图 #define MAX_VERTEX_NUM 20 // 弧结点 typedef struct ArcBox{ int tailvex, headvex; struct ArcBox *hlink, *tlink; InfoType *info; }ArcBox; 34/106 7.2 图的存储结构-十字链表 十字链表—有向图 //顶点结点 typedef struct VexNode{ VertexType data; ArcBox *firstin, *firstout; }VexNode; // 十字链表 typedef struct{ VexNode xlist[MAX_VERTEX_NUM]; int vexnum, arcnum; }OLGraph; 35/106 7.2 图的存储结构-邻接多重表 邻接多重表—无向图 (P166) 无向图 邻接表-每条边对应2个表结点 多重邻接表— 边结点数==边数 mark ivex ilink jvex jlink info 边结点 顶点结点 data firstedge 标记该边是否被搜索过 该边依附的一个顶点在 图中的位置 指向下一条依附于 顶点ivex的边 第一条依附于该顶点的边 36/106 7.2 图的存储结构-邻接多重表 邻接多重表—无向图 #define MAX_VERTEX_NUM 20 typedef enum { unvisited, visited} VisitIf; // 边结点 typedef struct EBox{ VisitIf mark; int ivex, jvex; struct EBox *ilink, *jlink; InfoType *info; }EBox;

7.2图的存储结构-邻接多重表 7.3图的遍历(1) 邻接多重表一无向图 。图的遗历 ∥顶,点结点 顶点之间的邻接关系m:n typedef struct Vex Boxf VertexType data; 引入访问标志数组visited0.n-1],防止顶点多 EBox *firstedge; 次被访问 VexBox: 。图的遗历种类 川邻接多重表 。深度优先遍历:→树的先序遭历 typedef structf 从莱顶点出发,访问该顶点,然后依次从的来被访 Vex Box adjmulist[MAX_VERTEX_NUM]; 问的邮接点出发派度优先通历图,直至图中所有和有 int vexnum,edgenum; AMLGraph; 回 路径相通的顶燕虾被访问到: 38106 ☑图 7.3图的遍历(2) 7.3图的遍历(3) ·图的速历种类 ·广度优先遵历:)树的层次遭历 从某顶旅”出发,访问被顶点,然后依次访问v的所有 来曾访问过的你接点,再分别从这些邻接点出发依次 访问它们的怀接点,并使“先放拉问的顶点的邻接点 先于“后被过问的顶点的年接点”放黄问,直至用中所 有已被访问的项成的饰接点都被访问到: 生成树 。若困中还存在尚来访问过的顶点,则另选图中一个来 遍历序列 曹被访问的项点作起地点,继续重复上述过程 深度优先旋素(DS) 广度优先校素(BFS) 39/106 回 V V2 Vi VsVs VV V7 0H06 ViV2VaViVsVaV,Vs 图 基于ADT Graphe的DFS算法(算法7.4和7.5) 73图的遍4) Boolean visited[MAX VERTEX NUMI: void DFSTraverse(Graph G,Status (*Visit)(Graph G.int v)) DFSTraverse(G) for (v-0;v<G.vexnum;++v)visitedlv]=FALSE; ,基于ADT Graph for (v-0;v <G.vexnum;++v) if (!visited v) ·基于某种在储结构:邻接矩阵/邻接表/十字链 DFS(G,v,Visit); 表/邻接多重表 ■BFSTraverse(G) void DFS(Graph G,int v,Status (*Visit)(Graph G,int v)) ,基于ADT Graph visitedlv]=TRUE;Visit(G,v); ,基于某种存储结构:邻接矩阵/邻接表/十字链 for (w-FirstAdjVex(G,v);w;w-NextAdjVex(G,v,w)) 表/邻接多重表 if (visitedwl) DFS(G.w.Visit): 41/106 图 42/106
37/106 7.2 图的存储结构-邻接多重表 邻接多重表—无向图 // 顶点结点 typedef struct VexBox{ VertexType data; EBox *firstedge; }VexBox; //邻接多重表 typedef struct{ VexBox adjmulist[MAX_VERTEX_NUM]; int vexnum, edgenum; }AMLGraph; 38/106 7.3 图的遍历(1) 图的遍历 顶点之间的邻接关系m : n 引入访问标志数组visited[0..n-1],防止顶点多 次被访问 图的遍历种类 深度优先遍历:Æ 树的先序遍历 从某顶点v 出发,访问该顶点,然后依次从v 的未被访 问的邻接点出发深度优先遍历图,直至图中所有和v 有 路径相通的顶点都被访问到; 39/106 7.3 图的遍历(2) 图的遍历种类 广度优先遍历:Æ 树的层次遍历 从某顶点v 出发,访问该顶点,然后依次访问v 的所有 未曾访问过的邻接点,再分别从这些邻接点出发依次 访问它们的邻接点,并使“先被访问的顶点的邻接点” 先于“后被访问的顶点的邻接点” 被访问,直至图中所 有已被访问的顶点的邻接点都被访问到; 若图中还存在尚未访问过的顶点,则另选图中一个未 曾被访问的顶点作起始点,继续重复上述过程 40/106 7.3 图的遍历(3) V1 V2 V3 V4 V5 V6 V7 V8 V1 V2 V3 V4 V5 V6 V7 V8 深度优先搜索(DFS) V1 V1 V2 V2 V4 V4 V8 V5 V8 V5 V3 V3 V6 V6 V7 V7 生成树 遍历序列 广度优先搜索(BFS) V1 V1 V2 V2 V3 V3 V4 V4 V5 V5 V6 V6 V7 V7 V8 V8 最短 路径! 41/106 7.3 图的遍历(4) DFSTraverse(G) 基于ADT Graph 基于某种存储结构:邻接矩阵/邻接表/十字链 表/邻接多重表 BFSTraverse(G) 基于ADT Graph 基于某种存储结构:邻接矩阵/邻接表/十字链 表/邻接多重表 42/106 基于ADT Graph的DFS算法(算法7.4和7.5) Boolean visited[MAX_VERTEX_NUM]; void DFSTraverse(Graph G, Status ( *Visit ) (Graph G, int v) ) { for ( v = 0; v < G.vexnum; ++v ) visited[v] = FALSE; for ( v = 0; v < G.vexnum; ++v ) if ( !visited[v] ) DFS(G, v, Visit); } void DFS(Graph G, int v, Status ( *Visit ) (Graph G, int v) ) { visited[v] = TRUE; Visit(G, v); for ( w = FirstAdjVex(G, v); w; w = NextAdjVex(G, v, w) ) if ( !visited[w] ) DFS(G, w, Visit); }

基于某种存储结构的DFS算法 基于某种存储结构的DFS算法 根据选择的存储结构,决定FirstAdjVex()和 根据选择的存储结构,决定FirstAdjVex()和 NextAdjVex()的实现,重新整合算法. NextAdjVex()的实现,重新整合算法. 如采用邻接矩阵表示法表示的图,则DFS算法 如采用邻接表表示法表示的图,则DFS算法如 下: 如下: void DFS(ALGraph G,int v, void DFS (MGraph G,intv, Status (*Visit)(MGraph G,int v)){ Status (*Visit )(ALGraph G,int v)){ visited[v]=TRUE;Visit(G,v); visited[v]=TRUE;Visit(G,v); for (w=0;wnextarc) if (G.ares[v]lwl.adj &&!visited[w]) DFS(G,w,Visit ) if (!visited[p->adjvex] T(n=0(m2 DFS(G,p->adjvex,Visit); T(n)=0(n+e) 43/106 基于ADT Graph的BFS算法(算法7.6 基于ADT Graph的BFS算法(算法7.6) void BFSTraverse(Graph G, Status(*Visit)(Graph G,int v)) 庐出队,访问出队元素的怀接点 DeQueue(Q,u); for (v=0;v<G.vexnum;++v) for w=FirstAdjVex(G,u);w; visited[v]=FALSE; w=NextAdjVex(G,u,w)) if (!visited[w] InitQueue (Q); 作访问u的未访问的邻接点并入队 for (v=0;v<G.vexnum;++v) if (!visited[v]){ visited[w]=TRUE;Visit(G,w); 产访问某连通分量的起始顶点,起,点入队 EnQueue(Q,w); }//end of if visited[v]=TRUE;Visit(G,v); EnQueue(Q,v); }//end of while }//end of if while(!QueueEmpty(Q)){ }//end of BFSTraverse BFS算法-采用邻接矩阵表示法表示的网 BFS算法-采用邻接矩阵表示法表示的网 void BFSTraverse(MGraph G, 卢出队,访问出队元素的怀接点刺 Status(*Visit)(MGraph G,int v)) DeQueue(Q,u); for w=0;w<G.vexnum;w++) for(v=0;v<G.vexnum;++v) if(G.arcs[u][w].adj!=INFINITY visited[v]FALSE; &&!visited[w]) InitQueue(Q); 庐访问u的未访问的邻接点并入队 for(v=0;v<G.vexnum;++v) visited[w]=TRUE;Visit(G,w); if (!visited[v]) EnQueue(Q,w); 作访问某连通分量的起始顶点,起,点入队制 )//end of if visited[v]=TRUE;Visit(G,v); }//end of while EnQueue(Q,v); }//end of if while(!QueueEmpty(Q)){ }//end of BFSTraverse T(=0(m2) 48/106
43/106 基于某种存储结构的DFS算法 根据选择的存储结构,决定 FirstAdjVex( )和 NextAdjVex( )的实现,重新整合算法。 如采用邻接矩阵表示法表示的图,则DFS算法 如下: void DFS (MGraph G, int v, Status ( *Visit ) (MGraph G, int v)){ visited[v] = TRUE; Visit(G, v); for ( w = 0; w nextarc) if (!visited[p->adjvex] ) DFS(G, p->adjvex, Visit); } T(n)=O(n+e) 45/106 基于ADT Graph的BFS算法(算法7.6) void BFSTraverse (Graph G, Status ( *Visit ) (Graph G, int v) ) { for ( v = 0; v < G.vexnum; ++v ) visited[v] = FALSE; InitQueue (Q); for ( v = 0; v < G.vexnum; ++v ) if ( !visited[v] ){ /* 访问某连通分量的起始顶点,起点入队 */ visited[v] = TRUE; Visit(G, v); EnQueue(Q, v); while( !QueueEmpty(Q) ){ 46/106 基于ADT Graph的BFS算法(算法7.6) /* 出队,访问出队元素的邻接点 */ DeQueue(Q,u); for ( w = FirstAdjVex( G, u) ; w ; w = NextAdjVex(G, u, w) ) if ( !visited[w] ){ /* 访问u的未访问的邻接点并入队 */ visited[w] = TRUE; Visit(G, w); EnQueue(Q, w); } //end of if } //end of while } //end of if } //end of BFSTraverse 47/106 BFS算法--采用邻接矩阵表示法表示的网 void BFSTraverse (MGraph G, Status ( *Visit ) (MGraph G, int v) ) { for ( v = 0; v < G.vexnum; ++v ) visited[v] = FALSE; InitQueue (Q); for ( v = 0; v < G.vexnum; ++v ) if ( !visited[v] ){ /* 访问某连通分量的起始顶点,起点入队 */ visited[v] = TRUE; Visit(G, v); EnQueue(Q, v); while( !QueueEmpty(Q) ){ 48/106 BFS算法--采用邻接矩阵表示法表示的网 /* 出队,访问出队元素的邻接点 */ DeQueue(Q,u); for ( w = 0 ; w < G.vexnum; w++ ) if ( G.arcs[u][w].adj != INFINITY && !visited[w] ){ /* 访问u的未访问的邻接点并入队 */ visited[w] = TRUE; Visit(G, w); EnQueue(Q, w); } //end of if } //end of while } //end of if } //end of BFSTraverse T(n)=O(n2)

BFS算法-采用邻接表表示法表示的网 BFS算法一采用邻接表表示法表示的网 void BFSTraverse (ALGraph G. Status(*Visit)(ALGraph G,int v)) 作出队,访问出队元素的邻接,点制 DeQueue(Q,u); for (v=0;vnextarc visited[v]FALSE; if (!visited[p->adjvex]){ InitQueue (Q); 访问u的未访问的你接点并入队 for (v=0;vadjvex ]TRUE; if (!visited[v]){ Visit(G,p->adjvex ) 庐访问某连通分量的起始顶点,起,点入队 EnQueue(Q,p->adjvex ) visited[v]=TRUE;Visit(G,v); }//end of if EnQueue(Q,v); }//end of while T(n)=O(n+e) while(!QueueEmpty(Q)){ }//end of if }//end of BFSTraverse 49/106 50/106 生73图的遍历-丰递归的DF5算法 73图的遍历-非递归的DFS算法 ·思路:DFS(G,v,Visit) 设量栈保存v和的相关信惠 。G为要遭历的图,V为遭历的起始顶点: ·在顺着w深度优先遗历之前,进行现场保护: 。在访问v后,需要顺着V的各个未访问过的邻接点深 。在顺着深度优先遭历结束后,进行现场恢复 度优先遗历一形成深度优先生成制,V可能存在 。栈顿的设计 多棵子树。 ·邻接矩阵:保存项点V和w的编号 。问愿:由V找到一个未访问过的邻接点w后,顺着 w深度优先遭历后,如何回到原先的V,找v的下一 ·邻接表:保存顶点V的编号和绑接点w在v的邻 接表中对应的表结点(或其后继)的指针。 个未访问的邻接点? 51/106 52/106 图 void DFS(Graph G,int v, Status (*Visit )(ALGraph G,int v)) InitStack(S); Visit(G,v);visited[v]=TRUE; 生7.3图的遍历-非递归的DF5算法 push(W,-l,S;∥假设顶,点编号是从0开始 ·对上页算法的评价 while (!StackEmpty(S)){ pop(S,Y,W); ·针对每个顶点V和其邻接点w,如果wW已经访问过 if (w==-1)w=FirstAdivex(G,v); 则也会入栈 else w=NextAdjvex(G,v,w); 一些入栈和出栈操作是不必要的,这会引起 ifw.=pusV,w,S阴 时间的开销 if (!visitedlw]) Visit(G,w);visited[w]=TRUE; ·思考 push(w,-1,S); ·如何修改算法,使得只将V和未访问过的邻接点 w入栈? 53/106 54/106 回
49/106 BFS算法--采用邻接表表示法表示的网 void BFSTraverse (ALGraph G, Status ( *Visit ) (ALGraph G, int v) ) { for ( v = 0; v nextarc ) if (!visited[p->adjvex] ){ /* 访问u的未访问的邻接点并入队 */ visited[p->adjvex ] = TRUE; Visit(G, p->adjvex ); EnQueue(Q, p->adjvex ); } //end of if } //end of while } //end of if } //end of BFSTraverse T(n)=O(n+e) 51/106 7.3 图的遍历—非递归的DFS算法 思路: DFS(G, v, Visit) G为要遍历的图,v为遍历的起始顶点; 在访问v后,需要顺着v的各个未访问过的邻接点深 度优先遍历——形成深度优先生成树,v可能存在 多棵子树。 问题:由v找到一个未访问过的邻接点w后,顺着 w深度优先遍历后,如何回到原先的v,找v的下一 个未访问的邻接点? 52/106 7.3 图的遍历—非递归的DFS算法 设置栈保存v和w的相关信息 在顺着w深度优先遍历之前,进行现场保护; 在顺着w深度优先遍历结束后,进行现场恢复 栈帧的设计 邻接矩阵:保存顶点v和w的编号 邻接表:保存顶点v的编号和邻接点w在v的邻 接表中对应的表结点(或其后继)的指针。 53/106 void DFS( Graph G, int v, Status ( *Visit ) (ALGraph G, int v) ){ InitStack(S); Visit(G, v); visited[v]= TRUE; push(v, -1, S); // 假设顶点编号是从0开始 while ( !StackEmpty(S)) { pop(S, v, w); if (w==-1) w = FirstAdjvex(G, v); else w = NextAdjvex(G, v, w); if ( w!=-1){ push(v, w, S); if ( !visited[w] ){ Visit(G, w); visited[w]= TRUE; push(w, -1, S); } } } } 54/106 7.3 图的遍历—非递归的DFS算法 对上页算法的评价 针对每个顶点v和其邻接点w,如果w已经访问过, 则也会入栈 Î一些入栈和出栈操作是不必要的,这会引起 时间的开销 思考 如何修改算法,使得只将v和未访问过的邻接点 w入栈?

7.3图的遍历-遍历算法的应用(1) 7,3图的遍历-遍历算法的应用(2) ■图的深度优先遍历 ■图的广度优先遍历 ,求一条包含图中所有顶点的简单路径(简单回 ·判断是否存在从顶点v到顶点的路径 路) ,求距0的各顶点中最瓶路径长度量长的一个顶 ,判断图中是否存在环 点 ,求图中通过给定顶点k的简单回路 ,求v0和v1之间的最短路径 ,判断是否存在从顶点v到顶点j的路径 ,在顶点子集U中找出距离顶点v0最近的顶点 ,求顶点v0到其余每个顶点的最短路径 ,判别v0和v1之间是否存在一条长度为k的路径 ,求距离顶点v0的最短略径长度为k的所有顶点 55/106 回 56/106 图 7.3图的遍历-遍历算法的应用(3) 士7.3图的遍历-遍历算法的应用(4) ■例1:求一条包含图中所有顶点的简单路径(简单 1 ·例1:求一条包含图中所有顶点的简单略径(简 回路) 4 单回路) (3 ·思路 ·1)起点的选择:如图(a),其符合题意的一 条简单路径如图(b)。若起点为1,则不能 。对于任意的有向图或无向图G,并不一定都能找到 (6 找到符合题意的简单路径: 符合题意的简单路径。它的查找可以基于深度优先 (a)e ① 2)顶点的邻接点次序:进一步考察图(), 通历。 (② 即使以2为起点,但是2的邻接点选择的是 ,在一个存在包含全部顶点的简单略径的图中,起点 ③ 1,而不是5,此时也不能找到符合题意的 的选择和顶点的邻接点次序会影响该简单略径是否 ⑤ 解。 能顺利地查到。 57/106 图 ⑥ (b) 58/106 图 7.3图的遍历-遍历算法的应用(5) ,在基于DFS的查找算法中,由于起点和邻接点的选 丰72图的阳 取与顶点和接点的左储达庄以及算法的擅赏次庄 回路) 有关,不可能依据特定的图给出特定的解决算法。 ,对DFS算法的修改 ,初始化计数器n,放在visited的初始化前或后; 因此,在整个搜察中应允许有查找失败,此时可采 ,访问顶点时,增加将该顶点序号加入到数组Path 取回溯到上一层的方法,继续查找其他路径。 中,计数器n十+; ,这样,引入数组Ph用来保存当前已撞蜜的简单监 判断是否已获得所求路径,是则输出结束,否则继 续遗历邻接点: 径上的顶点,引入计数器用来记录当前该路径上 ,某顶点的全部邻接点都访问后,仍未得到简单路 的顶点数。 径,则回湖,将该顶点置为未访问,计数器-~。 59/106 图 60/106 图
55/106 7.3 图的遍历—遍历算法的应用(1) 图的深度优先遍历 求一条包含图中所有顶点的简单路径(简单回 路) 判断图中是否存在环 求图中通过给定顶点vk的简单回路 判断是否存在从顶点vi到顶点vj的路径 判别v0和v1之间是否存在一条长度为k的路径 56/106 7.3 图的遍历—遍历算法的应用(2) 图的广度优先遍历 判断是否存在从顶点vi到顶点vj的路径 求距v0的各顶点中最短路径长度最长的一个顶 点 求v0和v1之间的最短路径. 在顶点子集U中找出距离顶点v0最近的顶点 求顶点v0到其余每个顶点的最短路径 求距离顶点v0的最短路径长度为k的所有顶点 57/106 7.3 图的遍历—遍历算法的应用(3) 例1:求一条包含图中所有顶点的简单路径(简单 回路) 思路 对于任意的有向图或无向图G,并不一定都能找到 符合题意的简单路径。它的查找可以基于深度优先 遍历。 在一个存在包含全部顶点的简单路径的图中,起点 的选择和顶点的邻接点次序会影响该简单路径是否 能顺利地查到。 58/106 7.3 图的遍历—遍历算法的应用(4) 例1:求一条包含图中所有顶点的简单路径(简 单回路) 1) 起点的选择:如图(a),其符合题意的一 条简单路径如图(b)。若起点为1,则不能 找到符合题意的简单路径; 2) 顶点的邻接点次序:进一步考察图(a), 即使以2为起点,但是2的邻接点选择的是 1,而不是5,此时也不能找到符合题意的 解。 59/106 7.3 图的遍历—遍历算法的应用(5) 在基于DFS的查找算法中,由于起点和邻接点的选 取与顶点和邻接点的存储次序以及算法的搜索次序 有关,不可能依据特定的图给出特定的解决算法。 因此,在整个搜索中应允许有查找失败,此时可采 取回溯到上一层的方法,继续查找其他路径。 这样,引入数组Path用来保存当前已搜索的简单路 径上的顶点,引入计数器n用来记录当前该路径上 的顶点数。 60/106 7.3 图的遍历—遍历算法的应用(6) 例1:求一条包含图中所有顶点的简单路径(简单 回路) 对DFS算法的修改 初始化计数器n,放在visited的初始化前或后; 访问顶点时,增加将该顶点序号加入到数组Path 中,计数器n++; 判断是否已获得所求路径,是则输出结束,否则继 续遍历邻接点; 某顶点的全部邻接点都访问后,仍未得到简单路 径,则回溯,将该顶点置为未访问,计数器n--