
Optimal Determination of Source-destination Connectivity in Random Graphs Luoyi Fu,Xinbing Wang,P.R.Kumar Dept.of Electronic Engineering Shanghai Jiao Tong University Dept.of Electrical Computer Engineering Texas A&M University
Optimal Determination of Source-destination Connectivity in Random Graphs Luoyi Fu, Xinbing Wang, P. R. Kumar Dept. of Electronic Engineering Shanghai Jiao Tong University Dept. of Electrical & Computer Engineering Texas A&M University
Random Graph:G(n,p)Model ●N nodes ● Each edge exists with probability p Proposed by Gilbert in 1959 ● Called ER graph 2/19
Random Graph: G(n,p) Model ⚫ N nodes ⚫ Each edge exists with probability p ⚫ Proposed by Gilbert in 1959 ⚫ Called ER graph 2/19
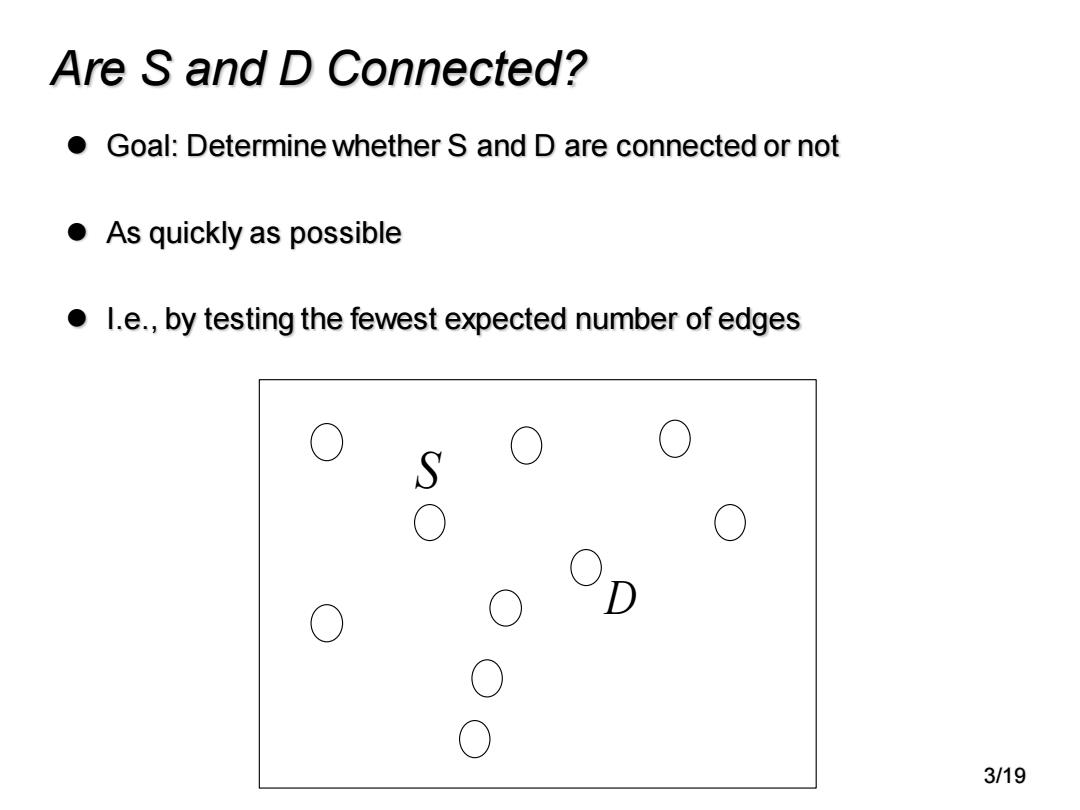
Are S and D Connected? o Goal:Determine whether S and D are connected or not ●As quickly as possible l.e.,by testing the fewest expected number of edges S O 0 D O 0 ○ 0 3/19
Are S and D Connected? ⚫ Goal: Determine whether S and D are connected or not ⚫ As quickly as possible ⚫ I.e., by testing the fewest expected number of edges S D 3/19
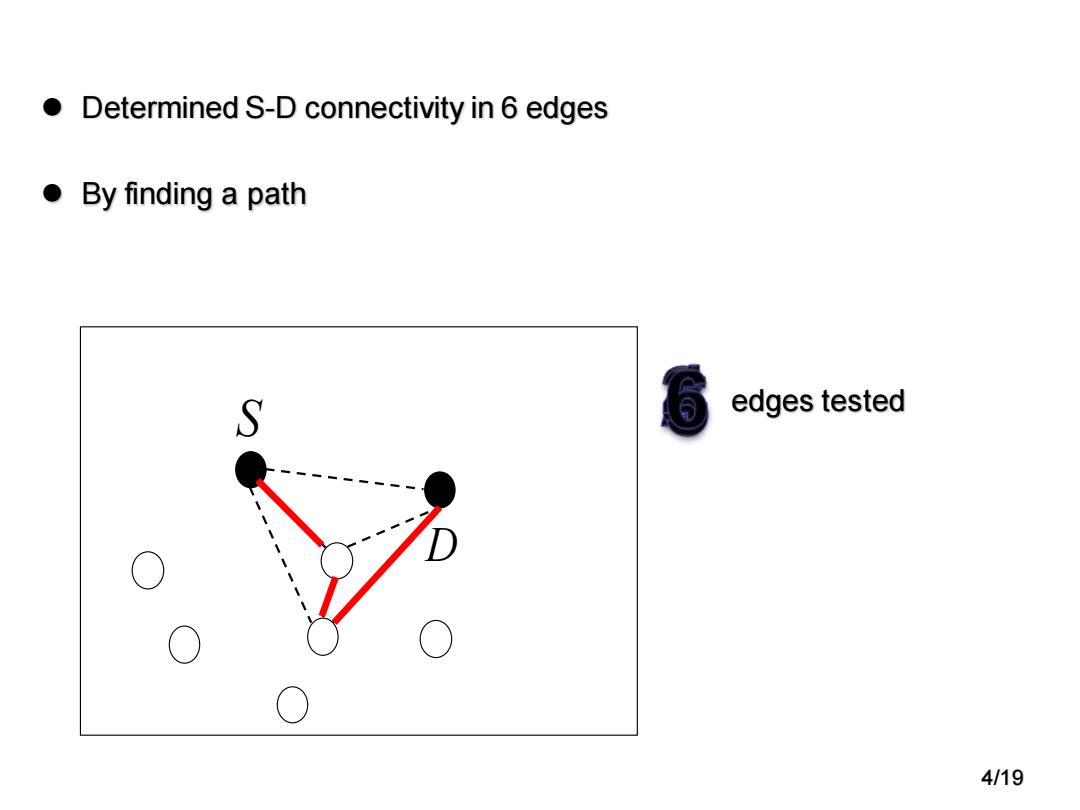
● Determined S-D connectivity in 6 edges ●By finding a path S edges tested O 4/19
⚫ Determined S-D connectivity in 6 edges ⚫ By finding a path S D edges tested 4/19
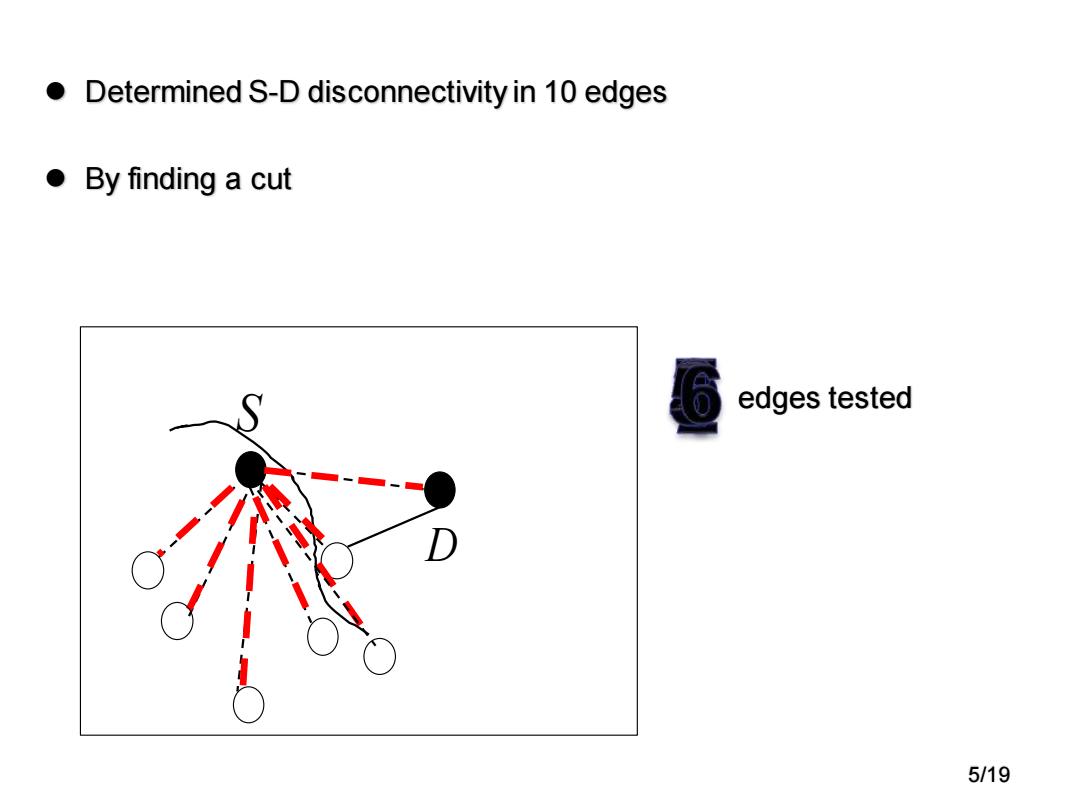
● Determined S-D disconnectivity in 10 edges ●By finding a cut 6 edges tested 5/19
⚫ Determined S-D disconnectivity in 10 edges ⚫ By finding a cut S D edges tested 5/19
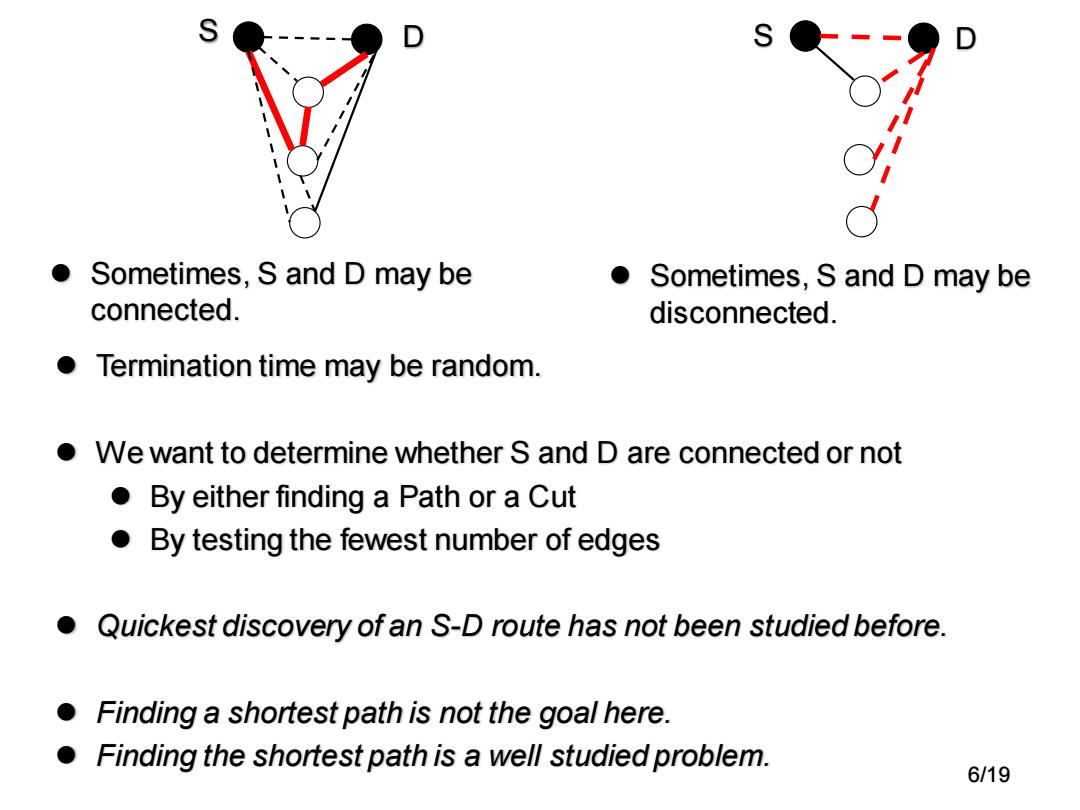
Sometimes,S and D may be ● Sometimes,S and D may be connected. disconnected. Termination time may be random. o We want to determine whether S and D are connected or not By either finding a Path or a Cut o By testing the fewest number of edges ● Quickest discovery of an S-D route has not been studied before. Finding a shortest path is not the goal here. Finding the shortest path is a well studied problem. 6/19
S D S D ⚫ Termination time may be random. ⚫ We want to determine whether S and D are connected or not ⚫ By either finding a Path or a Cut ⚫ By testing the fewest number of edges ⚫ Quickest discovery of an S-D route has not been studied before. ⚫ Finding a shortest path is not the goal here. ⚫ Finding the shortest path is a well studied problem. 6/19 ⚫ Sometimes, S and D may be connected. ⚫ Sometimes, S and D may be disconnected
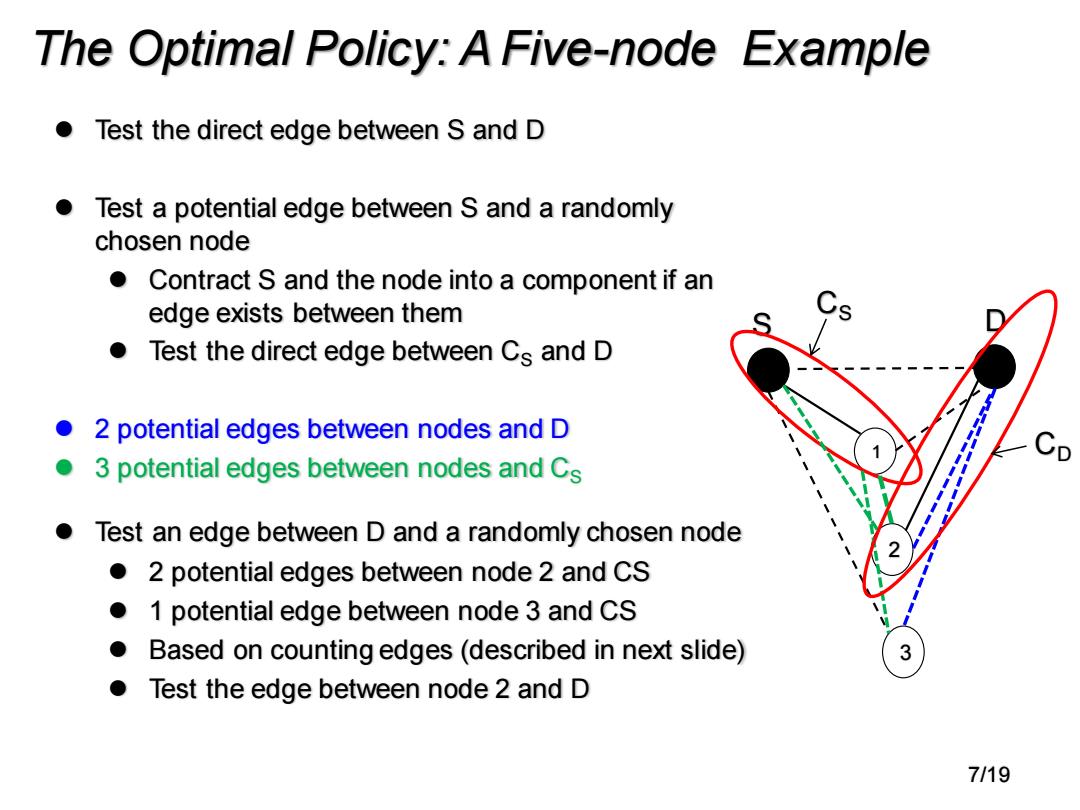
The Optimal Policy:A Five-node Example Test the direct edge between S and D Test a potential edge between S and a randomly chosen node ● Contract S and the node into a component if an edge exists between them Test the direct edge between Cs and D 2 potential edges between nodes and D 0 3 potential edges between nodes and Cs Test an edge between D and a randomly chosen node 2 potential edges between node 2 and CS ● 1 potential edge between node 3 and CS ● Based on counting edges(described in next slide) 3 Test the edge between node 2 and D 7/19
⚫ Test the direct edge between S and D ⚫ Test a potential edge between S and a randomly chosen node ⚫ Contract S and the node into a component if an edge exists between them ⚫ Test the direct edge between CS and D ⚫ 2 potential edges between nodes and D ⚫ 3 potential edges between nodes and CS ⚫ Test an edge between D and a randomly chosen node ⚫ 2 potential edges between node 2 and CS ⚫ 1 potential edge between node 3 and CS ⚫ Based on counting edges (described in next slide) ⚫ Test the edge between node 2 and D The Optimal Policy: A Five-node Example 1 3 2 S D CS CD 7/19
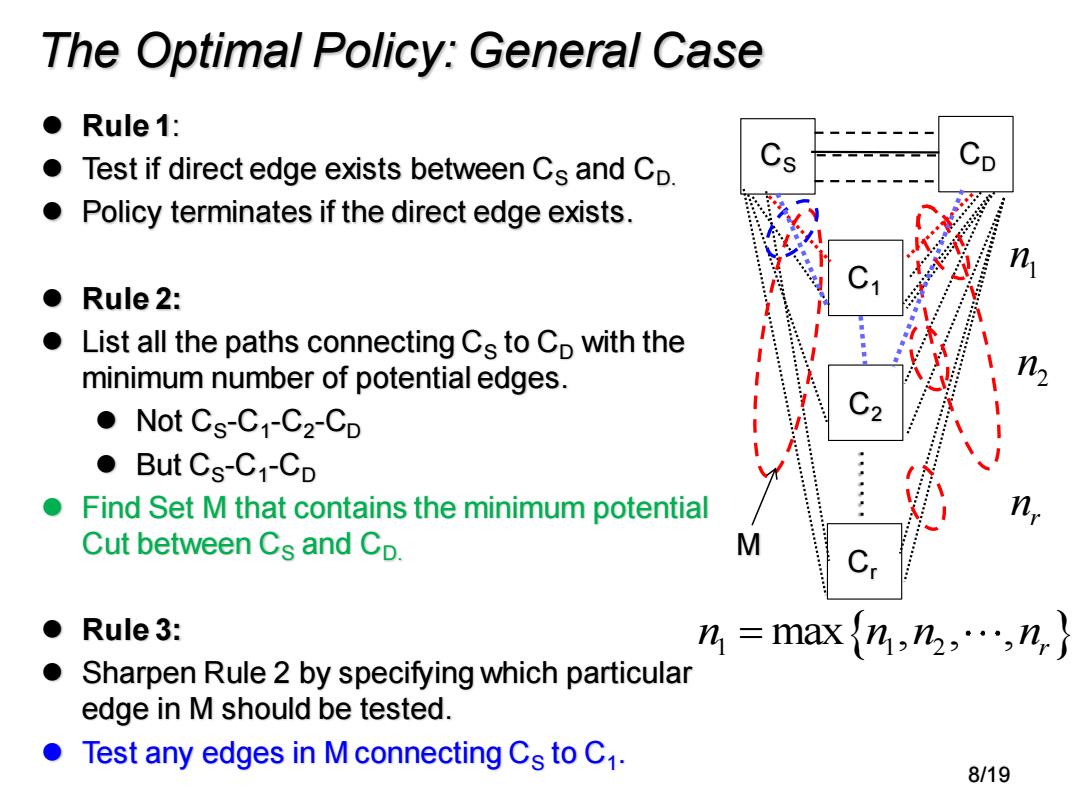
The Optimal Policy:General Case ●Rule1: Test if direct edge exists between Cs and CD. Cp Policy terminates if the direct edge exists. n ● Rule 2: List all the paths connecting Cs to Cp with the minimum number of potential edges. ●Not Cs-C1-C2-Co ●But Cs-C1-Co Find Set M that contains the minimum potential Cut between Cs and Cp. M ● Rule 3: n=max{h,n2,…,hn} Sharpen Rule 2 by specifying which particular edge in M should be tested. ● Test any edges in M connecting Cs to C1. 8/19
The Optimal Policy: General Case ……. ⚫ Rule 1: ⚫ Test if direct edge exists between CS and CD. ⚫ Policy terminates if the direct edge exists. ⚫ Rule 2: ⚫ List all the paths connecting CS to CD with the minimum number of potential edges. ⚫ Not CS-C1 -C2 -CD ⚫ But CS -C1 -CD ⚫ Find Set M that contains the minimum potential Cut between CS and CD. ⚫ Rule 3: ⚫ Sharpen Rule 2 by specifying which particular edge in M should be tested. ⚫ Test any edges in M connecting CS to C1 . CS CD C1 C2 Cr M 1 n 2 n r n n n n n 1 1 2 = max , , , r 8/19

Proof of Rule 1:Test If the Direct Edge Exists Testing the direct edge at the first step is better than testing at the second step. s回s-回 terminate s可s-可 terminate 个 Terminate one step earlier! Same A od probability bad oInduction on the number of edges tested before the direct edge is tested 9/19
Proof of Rule 1: Test If the Direct Edge Exists ⚫Testing the direct edge at the first step is better than testing at the second step. good Abad A S D S D S D S D S D S D S D S D S D S D terminate Same probability 9/19 ⚫Induction on the number of edges tested before the direct edge is tested terminate Terminate one step earlier!
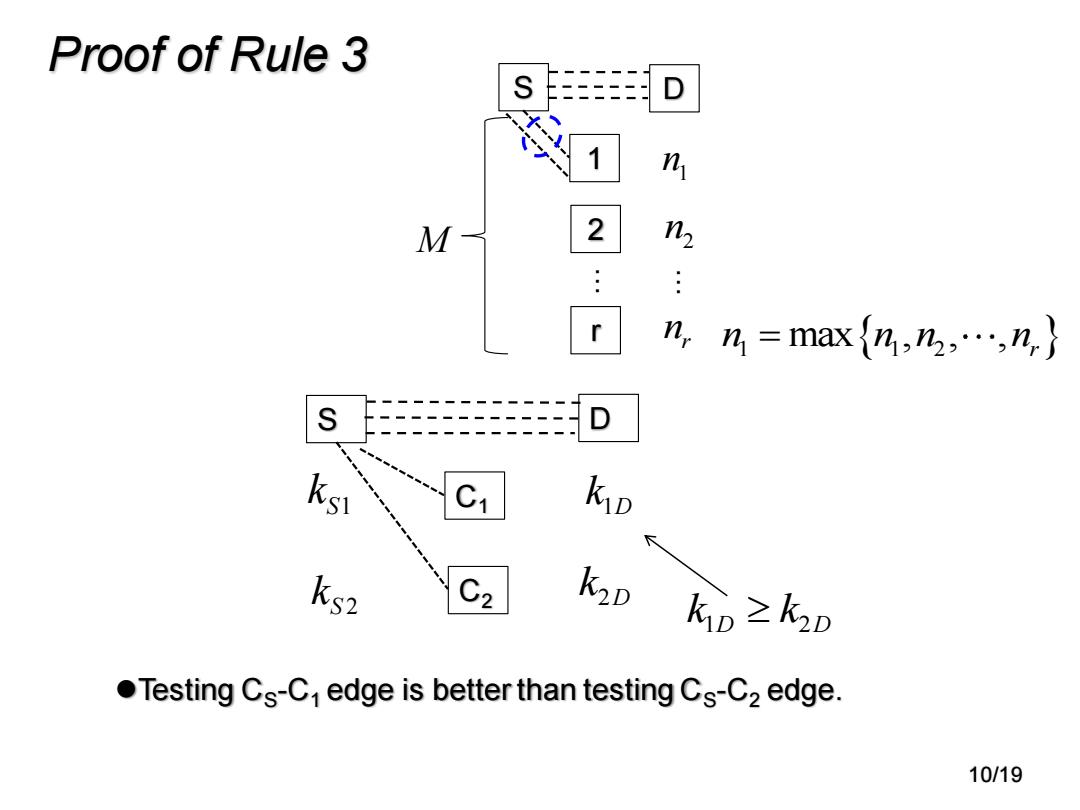
Proof of Rule 3 D n M 2 n r n,h=max{h,乃,…,n,} D C1 kD ks2 C2 KD kD≥k2D Testing Cs-C1 edge is better than testing Cs-C2 edge. 10/19
Proof of Rule 3 ⚫Testing CS-C1 edge is better than testing CS-C2 edge. S D C1 C2 1D k 2D k S1 k S 2 k 1 2 D D k k 10/19 S D 1 r 2 … 1 n 2 n r n … n n n n 1 1 2 = max , , , r M