
2009/12/29 数据结构 查找 第九章查找 重点:掌握顺序查找、折半查找、二叉排序 主讲:张昱 树上查找以及散列表上查找的基本思想和算 yuzhang@ustc.edu 法实现。 0551-3603804 难点:二叉排序树的删除算法及B-树上的插 入和副除算法。 1/103 2/10B 第九章查找 9.0一些定义:查找表 9.0二些定义 ■查找表(Search Table) ·定义:由同一类型的数据元素(或记录)构成的 9.1静态查找表 集合。 9.2劲态查找表 “集合”中的数据元素之间存在着完全松散的 关系查找表是一种非常灵便的数据结构 9.3哈希表 ·操作 。查询某个“特定的”数据元素是否在查找表中: ,检索某个“特定的”数据元素的各种属性; 3103 4103 图 生9.0一些定义:查找表及其分类 9.0一些定义-关键字 。操作 ■关键字 。在查找表中插入一个数据元素: ·定义:是数据元素(或记录)中某个数据项 。从查找表中副去某个数据元素。 的值,用以标识(识别)一个数据元素(或 。查找表的分类 记录)。 ,静态查找表:仅作查询和检索操作的查找表。 ·若此关键字可以唯一地标识一个记录,则称 ,动态查找表:在查询过程中同时擂入查找表中不 之为主关键字: 存在的数据元素,或者从查找表中副除已存在的 :若此关键字能识别若干记录,则称之为次关 莱个数据元素。 健字。 5/10 合 610 圄 1
2009/12/29 1 数据结构——查找 1/103 主讲:张昱 yuzhang@ustc.edu 0551-3603804 第九章 查找 2/103 重点:掌握顺序查找、折半查找、二叉排序 树上查找以及散列表上查找的基本思想和算 法实现。 难点:二叉排序树的删除算法及B-树上的插 入和删除算法。 第九章 查找 9.0 一些定义 9.1 静态查找表 3/103 9.2 动态查找表 9.3 哈希表 9.0 一些定义-查找表 查找表(Search Table) 定义:由同一类型的数据元素(或记录)构成的 集合 4/103 。 “集合”中的数据元素之间存在着完全松散的 关系查找表是一种非常灵便的数据结构 操作 查询某个“特定的”数据元素是否在查找表中; 检索某个“特定的”数据元素的各种属性; 9.0 一些定义-查找表及其分类 操作 在查找表中插入一个数据元素; 从查找表中删去某个数据元素。 5/103 查找表的分类 静态查找表:仅作查询和检索操作的查找表。 动态查找表:在查询过程中同时插入查找表中不 存在的数据元素,或者从查找表中删除已存在的 某个数据元素。 9.0 一些定义-关键字 关键字 定义:是数据元素(或记录)中某个数据项 的值,用以标识(识别)一个数据元素(或 6/103 的值,用以标识(识别) 个数据元素(或 记录)。 若此关键字可以唯一地标识一个记录,则称 之为主关键字; 若此关键字能识别若干记录,则称之为次关 键字

2009/12/29 9.0一些定义-查找 9.0一些定义-类型定义 。查找 typedef struct ·定义:根据给定的某个值,在查找表中确定一 KeyType key;关键字域 个其关健字等于给定值的记录或数据元素。 其它域 }ElemType; 若查找表中存在这样一个记录,则称查找 是成功的,此时查找结果为给出整个记录的信 根据具体的关键字类型,定义用于比较的、带参的宏 息,或指示该记录在查找表中的位置: #define EQ(a,b)... #define LT(a,b).… 否则称查找不成功,此时查找结果可给出 #define LQ(a,b)... 一个空记录或空指针。 7103 图 8/10 圄 戴帽时像D:具有相同特性的嫩元素的桌合。 9.1静态查找表 数关暴R:元素同属 一个桌合。 盖本操作P: Create(&ST,n) ▣抽象数据类型定义 操作结果:构造一个含个数拥元素的牌态查找表ST. Destroy(&ST) 。9.1.1顺序查找 初始条件,静态查找表ST存在 ,9.1.2有序表的查找 操作结果:轴服表ST. Search(ST,key) ·折半查控 初始条件静志查找表ST存在,key为和关幢字类型相同的始定值。 ,望波拉奥查找、播值查找 操作结果,若ST中存在其关能李等于key的数婚元来,则图数值为该 元素的值或在妻中的位置,否则为空” ■9.1.3整态树表的查找 Traverse(ST,Visit()) 。9.1.4索引顺序表的查找(分块查找】 初始条件静达查找表ST存在,Vs北是对元求作的应用西 操作结果:按某种洗序对5T的每个元家调用函数Vst)一次且仅一 次。一且Vst)失收,则操作失收 9110g 10/103 9.1.1顺序查找(1) 9.1.1顺序查找(2) 。查找表纳构:以顺序表或线性链表表示 ·对顺序麦的顺序查找 。基本思想:从一增开始向另一增,逐个进行记录的关健字 typedef struct( 和给定值的比较,若某个记录的关键字和给定值比校相等, ElemType*elem;数据元素存情空间蓬址 则查找成功:反之,若直至另一嘴,其关健字和给定值比 int length; 表长度 较都不等,则表明表中没有所查记录,查找不成功。 )SSTable; 查找成功示例: (34,44,4312,53,55,73,6477,kcy=64 查找不成功示例: 34,44,43,12,53,55,73,64,77,key=88 1y103 12/103 图 2
2009/12/29 2 9.0 一些定义-查找 查找 定义:根据给定的某个值,在查找表中确定一 个其关键字等于给定值的记录或数据元素 7/103 。 若查找表中存在这样一个记录,则称查找 是成功的,此时查找结果为给出整个记录的信 息,或指示该记录在查找表中的位置; 否则称查找不成功,此时查找结果可给出 一个空记录或空指针。 9.0 一些定义-类型定义 typedef struct { KeyType key; //关键字域 …… //其它域 8/103 } ElemType; 根据具体的关键字类型, 定义用于比较的、带参的宏 #define EQ(a, b) … #define LT(a, b) … #define LQ(a, b) … 9.1 静态查找表 抽象数据类型定义 9.1.1 顺序查找 912 有序表的查找 9/103 9.1.2 有序表的查找 折半查找 斐波拉契查找、插值查找 9.1.3 静态树表的查找 9.1.4 索引顺序表的查找(分块查找) ADT StaticSearchTable{ 数据对象D:具有相同特性的数据元素的集合。 数据关系R:数据元素同属一个集合。 基本操作P: Create(&ST, n) 操作结果:构造一个含n个数据元素的静态查找表ST. Destroy(&ST) 初始条件:静态查找表ST存在. 操作结果:销毁表ST. 10/103 Search(ST, key) 初始条件:静态查找表ST存在,key为和关键字类型相同的给定值. 操作结果:若ST中存在其关键字等于key的数据元素,则函数值为该 元素的值或在表中的位置,否则为“空”. Traverse(ST,Visit()) 初始条件:静态查找表ST存在,Visit是对元素操作的应用函数. 操作结果:按某种次序对ST的每个元素调用函数Visit()一次且仅一 次。一旦Visit()失败,则操作失败. } ADT StaticSearchTable 9.1.1 顺序查找(1) 查找表结构:以顺序表或线性链表表示 基本思想:从一端开始向另一端,逐个进行记录的关键字 和给定值的比较,若某个记录的关键字和给定值比较相等, 11/103 则查找成功;反之,若直至另一端,其关键字和给定值比 较都不等,则表明表中没有所查记录,查找不成功。 查找成功示例: (34, 44, 43, 12, 53, 55,73, 64, 77),key = 64 查找不成功示例: (34, 44, 43, 12, 53, 55,73, 64, 77),key = 88 9.1.1 顺序查找(2) 对顺序表的顺序查找 typedef struct{ ElemType *elem; //数据元素存储空间基址 12/103 int length; //表长度 }SSTable;

2009/12/29 9.1.1顺序查找(3) 9.1.1顺序查找(4) ■对顺序表的顺序查找 。性能分析 int Search_Seq(SSTable ST,KeyType key){ 。平均查找长度(4SL):为确定记录在查找表中的位置, ∥在序表5T中顺序查找其关铺字等于key的兼拥元素。 需和给定值进行比较的关键字个数的期望值。 ∥着找到,则函数值为该元素在表中的位量,否则为加。 T.elem.key=key:∥-兵” 。查找成功时 W从后往前找 ASLnP+(n-1)P++2P+P:nST.lengch for(i=ST.length;ST.elem[i].key!-key;-i); 假定P=1/n return i访找不到时,i为0 WSearch Sea -2-14-安 2 哨兵的作用:免去查找过程中每一步部要检测整个表是 ,查找不成功时 否查找完单。 ASL n+1 13103 备 14/103 圄 9.1.2有序表的查找-折半查找(1) 9.1.2有序表的查找-折半查找(2) ■折半查找(二分查找) 基本思想:查找区间逐步缩小(折半) ·查找表结构:有序表 查找不成功示例: ,基本思想:查找区间逐步缩小(折半) 123456789 查找成功示例: (12,33,40,45,53,55,64,66,77),key=68 123456789 (12,33,40,45,53,55,64,66,77),ky=64 tow id high ow指示查找区间的下界: high指示查找区间的上界; mid mid=(low+high)/2。 15103 16/103 图 9.1.2有序表的查找-折半查找(3) 9.1.2有序表的查找-折半查找(4) int Search_Bin (SSTable ST,KeyType key ) ow=1;high=sT.length;/置区间初值 。性能分析 while (low <high){ ,判定树:折半查找的查找过程可以用二叉树描述。 mid (low +high)/2; 。=ST.length=l0时,判定树的形态为: if (EQ(key,ST.elem[mid].key)) 查找成功时的4SL=该结点在 return mid;/找到传查元素 else if (LT(key,ST.elem[mid].key)) 2 8 判定树中的层次 high=mid-1;/在前区何进行查找 ASL sLlog2n小+1 ①③6( ⑨ else low=mid+1;/∥缝续在后半区间进行查找 查找不成功时 } AL≤Llog,n+1 return O; /佩序表中不存在种查元素 判定树的形态与m直接相关, }/∥Search_Bin 7/103 合 与关键字的取值无关 18/103 圄 3
2009/12/29 3 9.1.1 顺序查找(3) 对顺序表的顺序查找 int Search_Seq(SSTable ST, KeyType key) { // 在顺序表ST中顺序查找其关键字等于 key的数据元素。 // 若找到 则函数值为该元素在表中的位置 否则为0 13/103 // 若找到,则函数值为该元素在表中的位置,否则为0。 ST.elem[0].key = key; // “哨兵” // 从后往前找 for (i=ST.length; ST.elem[i].key!=key; --i); return i; //找不到时,i为0 } // Search_Seq 哨兵的作用:免去查找过程中每一步都要检测整个表是 否查找完毕。 9.1.1 顺序查找(4) 性能分析 平均查找长度(ASL):为确定记录在查找表中的位置, 需和给定值进行比较的关键字个数的期望值。 14/103 查找成功时 查找不成功时 ASL = n + 1 2 1 ( 1) 1 1/ ( 1) ... 2 , . 1 1 2 1 n n i n ASL P n ASL nP n P P P n ST length n i i n n 假定 9.1.2 有序表的查找-折半查找(1) 折半查找(二分查找) 查找表结构:有序表 基本思想:查找区间逐步缩小(折半) 15/103 查找成功示例: 1 2 3 4 5 6 7 8 9 (12, 33, 40, 45, 53, 55, 64, 66, 77),key = 64 low 指示查找区间的下界; high 指示查找区间的上界; mid = (low+high)/2。 low high mid low mid 9.1.2 有序表的查找-折半查找(2) 基本思想:查找区间逐步缩小(折半) 查找不成功示例: 1 2 3 4 5 6 7 8 9 16/103 (12, 33, 40, 45, 53, 55, 64, 66, 77),key = 68 low high mid low midlow mid low mid high high 9.1.2 有序表的查找-折半查找(3) int Search_Bin ( SSTable ST, KeyType key ) { low = 1; high = ST.length; // 置区间初值 while (low <= high) { mid = (low + high) / 2; 17/103 if (EQ (key , ST.elem[mid].key) ) return mid; // 找到待查元素 else if ( LT (key , ST.elem[mid].key) ) high = mid - 1; // 继续在前半区间进行查找 else low = mid + 1; // 继续在后半区间进行查找 } return 0; // 顺序表中不存在待查元素 } // Search_Bin 9.1.2 有序表的查找-折半查找(4) 性能分析 判定树:折半查找的查找过程可以用二叉树描述。 n=ST.length=10时,判定树的形态为: 18/103 2 ASL n log 1 5 2 8 1 3 6 9 4 7 10 查找成功时的ASL = 该结点在 判定树中的层次 判定树的形态与n直接相关, 与关键字的取值无关 查找不成功时 2 ASL n log 1

2009/12/29 9.1.2有序表的查找-折半查找(5) 9.1.2有序表的查找-斐波拉契查找 假设有序表的长度=21(反之h=og,(a+),则描述折 ·斐波拉契查找 半查找的判定树是深度为的满二叉树。树中层次为1的结 。查找表结构:有序表 点有1个,层次为2的结点有2个,层次为的结点有21个。 。基本思想:根据斐波拉突序列的特征对麦进行分削 假设表中年个记录的查找概率相等,则查找成功时折半查 找的平均查找长度 开始时表中记录个数比斐波拉契数小1,即n=F-1 将给定值key和sT.elemF.ke进行比较, _ntogn+)-l ,若相等,则查找成功: n 在>50时,可得近似结果 .若key<ST.elemF.key ASLlog2(n+1)-1 则壁续在ST.clem1.F1一1川中查找 191103 20/103 圄 9.1.2有序表的查找-斐波拉契查找 9.1.2有序表的查找-插值查找 ■斐波拉奥查找 。插值查找 ,否则,继续在sT.elemF+1F。-中查找 。查找表结构:有序表 前一子表长度是F1,后-于表长度是F1 ,盖本思想:根据给定值key来确定进行比较的关健字 ,平均性能比折半查找好,但最坏情况下的性能 ST.elemlil.key的查找方法 (虽然仍是0logn)却比折半查找差: key-ST.elem(n.key ST.clemSTelemIy() ·分剖时只需进行加、减运算 ST.clem和sT.clem川分别为有序表中具有最小关健 字和最大关键字的记录 2H/103 22/103 图 9.1.2有序表的查找-插值查找 9.1.3静态树表的查找(1) ·插值查找 。问题:描述查找过程的判定刺为何类二叉树时,其查找性 能最佳? 。插值查找只适于关健字均匀分布的表。 若判定树如左围,当各记录的查找振率 在这种情况下,对表长较大的顺序表,其平均性能比 相等时,查找成功时 折半查找好。 ASL=0.1*(1+2*2+3*4+43)=2.9 若各记录的查找振率不尊时,如0.05, Pw=0.15.其余为0.1, 则4SL-0.12-2+34+M-2+0.05+ 40.15-2.4+0.65-3.05 ⑦ 0若害牧时生和第6个记录的关接字比垫比 教不等时按折半查找,则 23/103 a 4
2009/12/29 4 9.1.2 有序表的查找-折半查找(5) 假设 有序表的长度n=2h-1(反之h=log2(n+1) ),则描述折 半查找的判定树是深度为h的满二叉树。树中层次为1的结 点有1个,层次为2的结点有2个,层次为h的结点有2h-1个。 19/103 log ( 1) 1 1 2 1 1 2 1 1 1 n n n j n C n ASL h j j n i bs i 假设表中每个记录的查找概率相等,则查找成功时折半查 找的平均查找长度 在 n>50 时,可得近似结果 ASLbs log2 (n 1) 1 9.1.2 有序表的查找-斐波拉契查找 斐波拉契查找 查找表结构:有序表 基本思想:根据斐波拉契序列的特征对表进行分割 20/103 开始时表中记录个数比斐波拉契数小1,即n = Fu-1 将给定值key和ST.elem[Fu-1].key进行比较, 若相等,则查找成功; 若key<ST.elem[Fu-1].key, 则继续在ST.elem[1..Fu-1-1]中查找 9.1.2 有序表的查找-斐波拉契查找 斐波拉契查找 否则,继续在ST.elem[Fu-1+1..Fu-1]中查找 前一子表长度是F -1 后一子表长度是F -1 21/103 前 子表长度是Fu-1 1 ,后 子表长度是Fu-2 1 平均性能比折半查找好,但最坏情况下的性能 (虽然仍是O(logn))却比折半查找差; 分割时只需进行加、减运算 9.1.2 有序表的查找-插值查找 插值查找 查找表结构:有序表 基本思想:根据给定值key来确定进行比较的关键字 22/103 基本思想:根据给定值key来确定进行比较的关键字 ST.elem[i].key的查找方法. ST.elem[l]和ST.elem[h]分别为有序表中具有最小关键 字和最大关键字的记录 . [ ]. ( 1) . [ ]. . [ ]. key ST elem l key i hl ST elem h key ST elem l key 9.1.2 有序表的查找-插值查找 插值查找 插值查找只适于关键字均匀分布的表。 在这种情况下 对表长较大的顺序表 其平均性能比 23/103 , ,其平均性能比 折半查找好。 9.1.3 静态树表的查找(1) 问题:描述查找过程的判定树为何类二叉树时,其查找性 能最佳? 若判定树如左图,当各记录的查找概率 相等时 查找成功时 24/103 5 2 8 1 3 6 9 4 7 10 相等时,查找成功时 ASL =0.1*(1+2*2+3*4+4*3)=2.9 若各记录的查找概率不等时,如P5=0.05, P10 = 0.15, 其余为0.1, 则ASL =0.1*(2*2+3*4+4*2)+0.05+ 4*0.15 = 2.4+0.65=3.05 若查找时先和第6个记录的关键字比较,比 较不等时再按折半查找,则 ASL = 0.1*(1+2*2+3*4+4)+0.2*4=2.9

2009/12/29 9.1.3静态树表的查找(2) 9.1.3静态树表的查找(3) PH值:定树的带权内略轻长度 次优查找树(Nearly Optimal Search Tree):若某个二又树的PH 如果只考也查找成功的情况, 值在所有具有同样权值的二又树中近似为最小,则称它为次忧查找 引入常量c,令e产p,(-12…n0,为结点的查找源率,则称为结 树。 点的权, PH=户为精银内每长度之和 次优查找树的构造 ·限个记影米速提地流能精一区,一-空限最小性 其中:m为二又树(判定前)上的结点个熏(即有序表的长虎:为 。分别对于序洲,4 一4和…构逢可操次忧查找满,并分 第:个结点在二又刺上的是次。 别设为根结赢的左子制和右子州。 ,静志最忧查找树Static Optimal Search Tree) 为便于计算△乃引入累计权值南w,=∑w,,并设4-5m4-0 一PH值取最小的二叉树, 构造静态最优责找树花费的时间代价校高1 =k--(m4-w4 =《4+w)-w-m- 25/103 26/103 圄 9.1.3静态树表的查找(4) 9.1.3静态树表的查找(5) 次优查找树的递归构造算法 例9-1(P223-224) Status SecondOptimal(BiTree &T,Elem Type Rl. fleat swl int low,int high)( 23 4 89 kev i abs(dw-swljl-sm-lmin)【 j:mi-abdw-swsm-l医 28 TBiTree)(izcof(BiTNode))exiOVERFLOW AP. 22 15 15 23 AP 1 6 9 8 7 AP AP, >rchild,B.sm,i+1,highk 271103 28/103 9.1.3静态树表的查找(6) 9.1.4索引顺序表的查找(1) 次优查找树构造算法的不足 在构造中未考察单个关健字的相应权值,则有可能出 ■分块查找(索引顺序查找) 现放选为根的关健字的权值比与它相邻的关健字的权值 小 ,查找表结构:以素引顺序表表示 调墓方法:进取邻近的权值较大的关键字作次优查找树的 ·起因 根结点。 ,顺序查找的不足:T(n)=O() 例9-2(略,P224) 。评价 :折半查找:T(n)=0(Iog2n),但要求查找表必须 ·大重实验表男,改优查找树和最代查找满的查找性能仅为 是有序表 12%,覆少超过3% 。基本思想:分块有序,索引表是有序表,索引 。构造次优查找满的算法的时间复杂度为0(logn) 次优查找树的查找过置类似于折半查找 项是(最大关键字,指针项) 29/108 合 30/103 圄 5
2009/12/29 5 9.1.3 静态树表的查找(2) PH值:判定树的带权内路径长度 如果只考虑查找成功的情况, 引入常量 c,令wi =cpi (i=1,2,…,n),(pi 为结点的查找概率),则称wi 为结 点的权 称 25/103 , 为带权内路径长度之和。 其中:n 为二叉树(判定树)上的结点个数(即有序表的长度);hi 为 第 i 个结点在二叉树上的层次。 静态最优查找树(Static Optimal Search Tree) ——PH值取最小的二叉树. 构造静态最优查找树花费的时间代价较高! 1 n i i i PH w h 9.1.3 静态树表的查找(3) 次优查找树(Nearly Optimal Search Tree):若某个二叉树的PH 值在所有具有同样权值的二叉树中近似为最小,则称它为次优查找 树。 次优查找树的构造 26/103 取第i个记录ri 构造根结点,使得 取最小值 (l≤i ≤h) 分别对子序列{rl , rl+1 , …, ri-1}和{ri+1 , …, rh}构造两棵次优查找树,并分 别设为根结点ri 的左子树和右子树. 为便于计算 ,引入累计权值和 ,并设wl-1 = swl-1 =0 1 1 h i i jj ji jl P w w P i i j j l sw w 1 1 1 1 ( )( ) ( ) i hi i l hl ii P sw sw sw sw sw sw sw sw 9.1.3 静态树表的查找(4) 次优查找树的递归构造算法 Status SecondOptimal(BiTree &T, ElemType R[], float sw[], int low, int high) { i=low; min = abs(sw[high]-sw[low]); dw = sw[high]+sw[low-1]; f (j l 1 j hi h j) 27/103 for (j=low+1; jdata = R[i]; if (i==low) T->lchild = NULL; else SecondOptimal(T->lchild, R, sw, low, i-1); if (i==high) T->rchild = NULL; else SecondOptimal(T->rchild, R, sw, i+1, high); return OK; } 9.1.3 静态树表的查找(5) 例9-1 (P223-224) j0123456789 keyj ABCDE FGH I 28/103 wj 0112534435 swj 0 1 2 4 9 12 16 20 23 28 ΔPj 27 25 22 15 7 0 8 15 23 ΔPj 11 9 6 1 9 8 1 7 ΔPj 312 0 0 0 ΔPj 0 0 9.1.3 静态树表的查找(6) 次优查找树构造算法的不足 在构造中未考察单个关键字的相应权值,则有可能出 现被选为根的关键字的权值比与它相邻的关键字的权值 小. 29/103 调整方法:选取邻近的权值较大的关键字作次优查找树的 根结点. 例9-2 (略,P224) 评价 大量实验表明,次优查找树和最优查找树的查找性能仅为 1%~2%,很少超过3% 构造次优查找树的算法的时间复杂度为O(nlogn) 次优查找树的查找过程类似于折半查找 9.1.4 索引顺序表的查找(1) 分块查找(索引顺序查找) 查找表结构:以索引顺序表表示 起因 30/103 顺序查找的不足:T(n) = O(n) 折半查找:T(n) = O(log2n),但要求查找表必须 是有序表 基本思想:分块有序,索引表是有序表,索引 项是(最大关键字, 指针项)

2009/12/29 9.1.4索引顺序表的查找(2) 9.1.4索引顺序表的查找(3) ■分块查找(索引顺序查找) ,分块查找过程 ·常引顺序表表示,分块有序,常引表是有序表 ·先确定待查记录所在的块(子表)一一有序表 。索引项是(最大关健字,指针项) 可以用折半查找或顺序查找 。再在块中查找 序表,,。,。。0 只能是顺序查找 170821191431332254052617846. ASL =L +L. 引表2404057810☐ L为查找索引表确定所在块的平均查找长度 L为在块中查找元素的平均查找长度 3103 32/103 圆 9.2动态查找表 9.2动态查找表-ADT(1) ■抽象数据类型定义 。特点:表结构本身是在查找过程中动态生成的 .ADT DynamicSearchTable ■9.2.1二叉排序树和平衡二叉撇 败据对象D:具有相同特性的数据元素的桌合。 败据关系R:数据元素同属一个集合。 ■9.2.2B-搬和B±樾 基本操作P: InitDSTable(&DT) ▣9.2.3键树 操作结果:构造一个空的动态查找表DT DestroyDSTable(&DT) 始条件:动态查找表DT存在 燥作结界:销毁表DT. 33/103 34/103 图 SearchDSTable(DT,key) 潮榨结共;动态者找表D工存在,k为和关牛类相同的给定慎 素的值或在表中的位置,否则为空”· 9.2.1二叉排序树:定义 InsertDSTable(&DT,e) 初始条件,动态查找表DT存在,e为特插入的数据元豪 ·二叉排序树(二叉查找树) 操作结果:着DT中不存在其关字于e.key的据元素,入e到 DT. Binary Sort/Search Tree DeleteDSTable(&DT,key) ,定义(递归):或者是一棵空树,或者是具有如 初始保件:动老查找表DT存在,key为和关德字类型相同的给定值 下特性的二叉树: 操作结果:若DT中存在其关塘李等于key的兼据元素,则除之 ,若它的左子树不空,则左子树上所直结点的值均小 TraverseDSTable(DT,Visit()) 初始条件:静老查找表DT存在,Vsit是对元素操作的应用西数. 王根结点的值: 操作结果:找某种次序对DT的年个元素调用西业Vs)一次且仅一次。 ,若它的右子树不空,则右子树上所直结点的值均太 一且Vst()失败,则操作失败 王根结点的值: }ADT DynamicSearchTable ,它的左、右子树也分别是二叉样序树。 合 36/103 圄 6
2009/12/29 6 9.1.4 索引顺序表的查找(2) 分块查找(索引顺序查找) 索引顺序表表示,分块有序,索引表是有序表 索引项是(最大关键字, 指针项) 31/103 ( , 0 1 2 3 4 5 6 7 8 9 10 11 12 13 …… 17 08 21 19 14 31 33 22 25 40 52 61 78 46 …… 21 0 40 5 78 10 …… 顺序表 索引表 9.1.4 索引顺序表的查找(3) 分块查找过程 先确定待查记录所在的块(子表)--有序表 可以用折半查找或顺序查找 32/103 再在块中查找 只能是顺序查找 为在块中查找元素的平 均查找长度 为查找索引表确定所在 块的平均查找长度 w b bs b w L L ASL L L 9.2 动态查找表 抽象数据类型定义 9.2.1 二叉排序树和平衡二叉树 33/103 叉排序树和平衡 叉树 9.2.2 B-树和B+树 9.2.3 键树 9.2 动态查找表-ADT(1) 特点:表结构本身是在查找过程中动态生成的 ADT DynamicSearchTable{ 数据对象D:具有相同特性的数据元素的集合。 34/103 数据关系R:数据元素同属一个集合。 基本操作P: InitDSTable(&DT) 操作结果:构造一个空的动态查找表DT. DestroyDSTable(&DT) 初始条件:动态查找表DT存在. 操作结果:销毁表DT. SearchDSTable(DT, key) 初始条件:动态查找表DT存在,key为和关键字类型相同的给定值. 操作结果:若DT中存在其关键字等于key的数据元素,则函数值为该元 素的值或在表中的位置,否则为“空”. InsertDSTable(&DT, e) 初始条件:动态查找表DT存在,e为待插入的数据元素. 操作结果:若DT中不存在其关键字等于e.key的数据元素,则插入e到 DT. DeleteDSTable(&DT key) 35/103 DeleteDSTable(&DT, key) 初始条件:动态查找表DT存在,key为和关键字类型相同的给定值. 操作结果:若DT中存在其关键字等于key的数据元素,则删除之. TraverseDSTable(DT,Visit()) 初始条件:静态查找表DT存在,Visit是对元素操作的应用函数. 操作结果:按某种次序对DT的每个元素调用函数Visit()一次且仅一次。 一旦Visit()失败,则操作失败. } ADT DynamicSearchTable 9.2.1 -二叉排序树:定义 二叉排序树(二叉查找树) Binary Sort/Search Tree 定义(递归) 或者是一棵空树 或者是具有如 36/103 定义(递归):或者是一棵空树,或者是具有如 下特性的二叉树: 若它的左子树不空,则左子树上所有结点的值均小 于根结点的值; 若它的右子树不空,则右子树上所有结点的值均大 于根结点的值; 它的左、右子树也分别是二叉排序树

2009/12/29 9.2.1-二叉排序树:查找举例 9.2.1-二叉排序树:查找算法 ·查找算法(算法9.5(a)) 基于二叉树先序遭历 BiTree SearchBST(BiTree T,KeyType key){ 查找key=70? ∥在根指针T所指二叉排序树中查找某关键字等于 23 66 ∥ky的数据元素,若查找成功,则返回指向该数据 查找key=28? 元素结点的指针,否则返回空指针 097099 f(TEQ(key,T->data.key》return(T:∥查找结束 else if(LT(key,T->data.key)) return(SearchBST(T->lchild,key)); else return(SearchBST(T->rchild,key)); 371103 备 38/103 圄 9.2.1-二叉排序树:插入 9.2.1-二叉排序树:改进的查找算法 二叉排序树的插入 。改写查找算法为算法9.5(b): 。新插入的结点一定是一个新深加的 Status SearchBST(BiTree T.KeyType key,BiTree f.BiTree &p){ 叶子结点并且是查找不成功时查找 33 ∥若查找成功,则指针指南试最调元素结点,并运图 略径上访问的最后一个结点的左孩 ∥T取UE,否则指针推向查找路径上访间的最后一个结点并 子或右盛子结点 运回FALSE,指针指向T的京亲:其初地调用值为NUL山 ,示例:从空树出发,待插的关镀字 if (T)(p-f;return FALSE; ebse if (EQ(key,T->data.key))(p-T;return TRUE:} 序列为33,44,23,46,12,37 else if (LT(key,T->data.key)) 中序遗历二叉排序树可得到一个关键字的有序序列。 return SearehBST(Tlchild,key.T,p): 该例中,中序遗历结果为:12,23,33,37,44,46 else return SearchBST(Trchild,key,T,p): 39/103 40/103 图 9.2.1-二叉排序树:插入算法 9.2.1-二叉排序树:删除1 ·二叉排序树的擂入算法9.6: ■二叉排序树的副除 Status Ins ertBST(BiTree &T,ElemType e) ∥当二又排序刺T中不存在关辅字等于:key的兼烟元素时,插 假设被副结点为°p,其双亲结点为*, 入e并返回IRLE:否则延回FAL.SE 。*p为叶子结点:副去*p,并修政f的孩子域。 if(SearchBST(T,e.key,NLp){H查找不成功 ,p只有左子树P或只有右子树Pk:令P或P.直接成 s-(BiTree)malloc(sizeof(BiTNode)): data-e;slchild -s->rchild-NULL: 为的子树 (p)T∥被结点为新的视结点 33 else if(LT(e.key,p->data.key))p>lchild-s p>rchild一s∥被插结点为右孩子 return TRUE; }else return FALSE:∥树中已有关字湘同的点,不再入 12 41/103 42/103 圄 7
2009/12/29 7 9.2.1 -二叉排序树:查找举例 45 23 66 查找key=70? 37/103 4 34 48 30 44 87 70 99 36 69 查找key=28? 9.2.1 -二叉排序树:查找算法 查找算法( 算法9.5(a) ) ——基于二叉树先序遍历 BiTree SearchBST(BiTree T, KeyType key){ // 在根指针T所指二叉排序树中查找某关键字等于 38/103 // key的数据元素,若查找成功,则返回指向该数据 //元素结点的指针,否则返回空指针 if (!T || EQ(key, T->data.key)) return (T); // 查找结束 else if (LT(key, T->data.key) ) return(SearchBST(T->lchild, key)); else return(SearchBST(T->rchild, key)); } 9.2.1 -二叉排序树: 插入 二叉排序树的插入 新插入的结点一定是一个新添加的 叶子结点,并且是查找不成功时查找 33 39/103 路径上访问的最后一个结点的左孩 子或右孩子结点. 示例:从空树出发,待插的关键字 序列为33,44,23,46,12,37 23 44 12 37 46 中序遍历二叉排序树可得到一个关键字的有序序列。 该例中,中序遍历结果为:12, 23, 33, 37, 44, 46 9.2.1 -二叉排序树:改进的查找算法 改写查找算法为算法9.5(b): Status SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p){ // 若查找成功,则指针p指向该数据元素结点,并返回 // TRUE 否则指针 指向查找路径上访问的最后 个结点并 40/103 // TRUE;否则指针p指向查找路径上访问的最后一个结点并 //返回FALSE。指针f 指向T的双亲,其初始调用值为NULL if (!T) { p=f; return FALSE;} else if ( EQ(key, T->data.key)) { p=T; return TRUE; } else if ( LT(key, T->data.key) ) return SearchBST(T->lchild, key, T, p); else return SearchBST(T->rchild, key, T, p); } 9.2.1 -二叉排序树:插入算法 二叉排序树的插入算法9.6: Status InsertBST(BiTree &T, ElemType e){ // 当二叉排序树T中不存在关键字等于e.key的数据元素时,插 //入e 并返回TRUE;否则返回FALSE 41/103 if (!SearchBST(T, e.key, NULL, p)) { // 查找不成功 s = (BiTree)malloc(sizeof(BiTNode)); s->data = e; s->lchild = s->rchild = NULL; if ( !p) T=s; // 被插结点*s为新的根结点 else if ( LT(e.key, p->data.key)) p->lchild=s; else p->rchild = s; // 被插结点*s为右孩子 return TRUE; } else return FALSE; // 树中已有关键字相同的结点,不再插入 } 9.2.1 -二叉排序树:删除1 二叉排序树的删除 假设被删结点为*p,其双亲结点为*f, *p为叶子结点:删去*p,并修改*f 的孩子域。 42/103 p p *p只有左子树PL或只有右子树PR:令PL或PR直接成 为*f 的子树 33 23 44 12 37 46 33 23 44 12 46 45 46 45 46

2009/12/29 9.2.1-二叉排序树:删除2 9.2.1-二叉排序树删除3 ·二叉排序树的副除 ·二叉排序树的副除 ,*p的左子树P和右子树Pπ均不为空 ■*p的左子树P和右子树P均不为空 方法L、P粳普p成为f的 33 方2、与方法1对称,P接普 到 子树,P成为P最右下结 233 33 p成为f的子树,P成为P最 3 3 点(中序塘历P,所得序列的 左下结点(中序遗历P.所得序列 ④ 的第一个结点)的左子树, 46 最后一个结点)的右子树, 3 4 38 46 40 40 50 这种方法可能会导致二 叉岸序树高度的增长1 35 40 4048 38 48 本例中高度:5→6 8 38 48 4310 44/10 合 9.2.1-二叉排序树:删除4 9.2.1-二叉排序树:删除5 ,二叉排序树的除 ·二叉排序树的副除 。*p的左子树P和右子树P均不为空 ·p的左于树P和右子树P均不为空 测除时,如何不增长树的高度? 33 方法4、与方法3对称,令*p 33 方法老、令“p的中序遗历的直 23 4④ 的中序速历的直接后维誉代 接前驱替代p,再从二叉排 *p,再从二叉排序刺中副去 序树中副去它的直捷前驱。 37 46 它的直接后维。 这种方法不会导致二叉 35 38 35 4048 排序树高度的增长1 本例中高度:5→5 48 38 45/103 合 46/103 9.2.1-二叉排序树:删除算法 9.2.1-二叉排序树:删除算法 ·二叉排序制的则膝算法9.7 。算法9.8从二又排序树中除p教向的结点 Sta ree &T. KeyType key Status Delete BiTree) 二叉排序树T中存在关幢字等于ky的业据元素时,副除该 if(p->rchild)fq-rpp>lchild:free(q}∥右子树为空 eeif(p>ehid)q-prp>rhid:req}∥左子树为空 ∥元素结点并返回TRUE:否则氪回FAL.SE else if (T)return FALSE: q-p:s-p->lchild; ebe{ while(s>rehild){g-s;s一s>eh山:}H使物向被结点的前易 if EQ(key,T->data.key)) pdata-sdata; return Dele(T片∥找到关精字等于key的量拥元素 if(q!=p)g->rchild=s>rchild; else if (LT(key,Tdata.key)) else g->lchild-s>lchild; return DeleteBST(Tlchild,keyy: free(s): else return DeleteBST(T>rehild,key) return TRUE: 471103 48/103 画 8
2009/12/29 8 9.2.1 -二叉排序树:删除2 二叉排序树的删除 *p的左子树PL和右子树PR均不为空 方法1、P 33 L 接替*p成为*f 的 43/103 33 23 44 12 37 46 40 50 48 35 38 46 50 48 23 12 37 35 40 38 方法 L 接替 p 子树, PR成为PL最右下结 点(中序遍历PL所得序列的 最后一个结点)的右子树。 40 这种方法可能会导致二 叉排序树高度的增长! 本例中高度:56 9.2.1 -二叉排序树:删除3 二叉排序树的删除 *p的左子树PL和右子树PR均不为空 方法2、与方法1对称,PR 接替 44/103 48 46 50 33 23 44 12 37 46 40 50 48 35 38 33 23 12 R *p成为*f 的子树, PL成为PR最 左下结点(中序遍历PR所得序列 的第一个结点)的左子树。 46 37 35 40 38 9.2.1 -二叉排序树:删除4 二叉排序树的删除 *p的左子树PL和右子树PR均不为空 删除时,如何不增长树的高度? 33 45/103 方法3、令*p的中序遍历的直 接前驱替代*p,再从二叉排 序树中删去它的直接前驱。 这种方法不会导致二叉 排序树高度的增长! 本例中高度:55 33 23 44 12 37 46 40 50 48 35 38 40 38 9.2.1 -二叉排序树:删除5 二叉排序树的删除 *p的左子树PL和右子树PR均不为空 方法4 与方法3对称 令*p 33 46/103 方法4、与方法3对称,令*p 的中序遍历的直接后继替代 *p,再从二叉排序树中删去 它的直接后继。 33 23 44 12 46 50 48 37 35 40 38 46 46 48 50 48 50 9.2.1 -二叉排序树:删除算法 二叉排序树的删除算法9.7 Status DeleteBST(BiTree &T, KeyType key){ // 当二叉排序树T中存在关键字等于key的数据元素时,删除该 数据 // 元素结点并返回TRUE 否则返回FALSE 47/103 // 元素结点并返回TRUE;否则返回FALSE if ( !T ) return FALSE; else { if ( EQ(key, T->data.key)) return Delete(T); // 找到关键字等于key的数据元素 else if ( LT(key, T->data.key)) return DeleteBST(T->lchild, key); else return DeleteBST(T->rchild, key); } } 9.2.1 -二叉排序树:删除算法 算法9.8 从二叉排序树中删除 p 指向的结点 Status Delete (BiTree &p){ if ( !p->rchild ) { q = p; p=p->lchild; free(q); } // 右子树为空 else if ( !p->lchild ){ q = p; p=p->rchild; free(q); } // 左子树为空 l { 48/103 else { q = p; s = p->lchild; while ( s->rchild ) { q=s; s=s->rchild; } // 使s 指向被删结点的前驱 p->data = s->data; if ( q!=p ) q->rchild = s->rchild; else q->lchild = s->lchild; free(s); } return TRUE; }
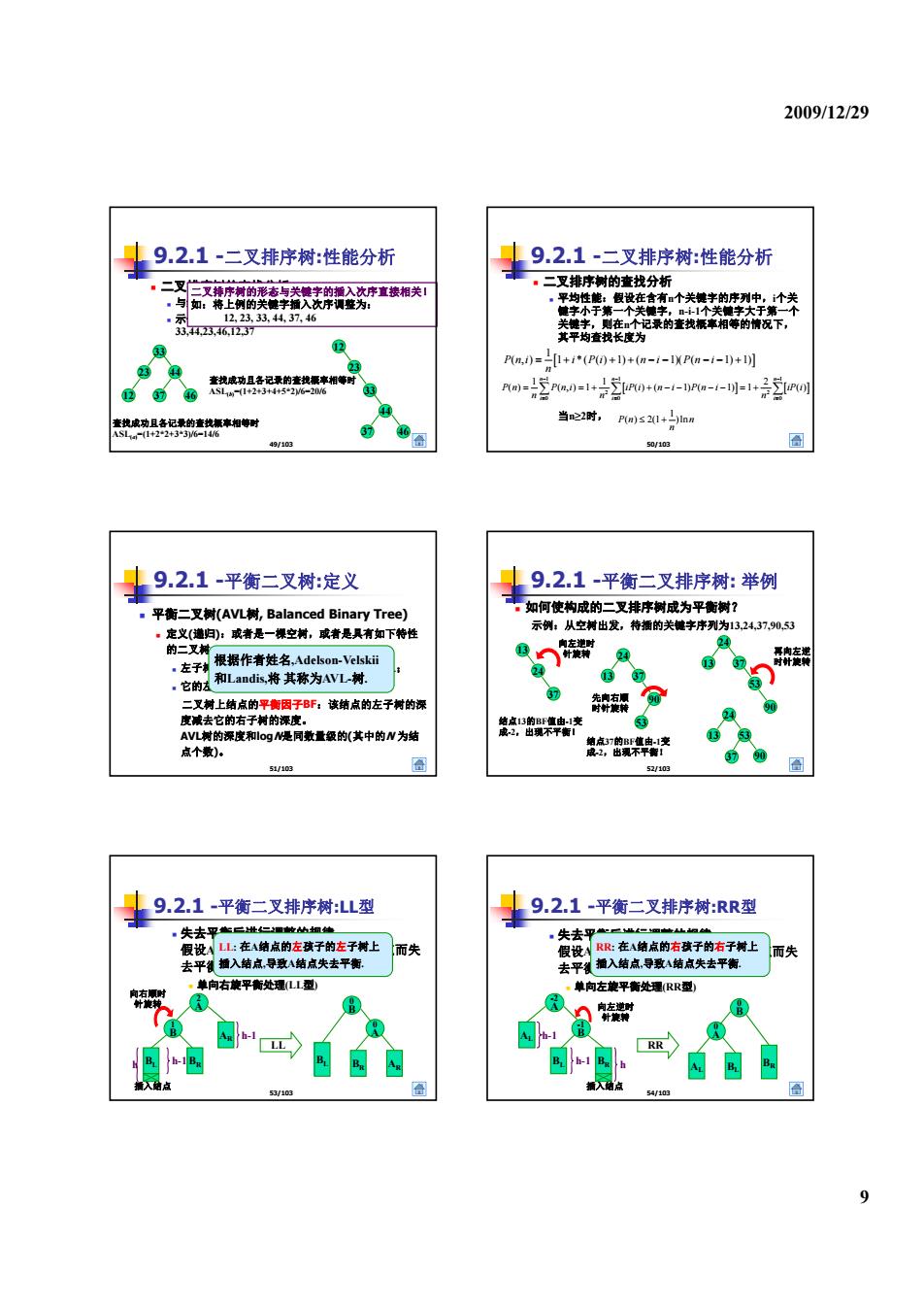
2009/12/29 9.2.1-二叉排序树:性能分析 9.2.1-二叉排序树:性能分析 。二叉仁文排序精的形卷与关健字的播入沈序直接相关] ·二叉排序树的查找分析 ,与如:将上例的关使字描入次序调整为: 12,23.33.44,37,46 "特个牛 33,442,46.27 关键主,则在和个记录的壹找擦率相等的情况下, a 其平均查找长度为 4 23 P)=+i*(P0++a-1-lXPn--+) 查找成功且各记录的查找据 率相等时 3 46 ASL11+2+3+4+52v6-206 nm-2=i+0ta-a-明=1+0 慧相 当22时, P(a)2(+ 49/102 50/103 圄 9.2.1-平衡二叉树:定义 9.2.1-平衡二叉排序树:举例 ,平衡二叉树AVL树,Balanced Binary Tree) :如何使构成的二叉排序树成为平衡树? ·定义(递):或者是一裸空树,或者是具有如下特性 示例:从空树出发,待插的关键字序列为13,24,37.90.53 的二叉树 3 南左逆时 24 根据作者姓名,Adelson-Velskii 、针旋转 得向左逆 ,左子制 3 3 时旋转 24 33 。它的左 和Landis,将其称为AVL-树. 3 二叉树上结点的平衡因子BF:该结点的左子树的深 先南右原 时外度传 度减去它的右子树的深度。 结点13的BF值由-1变 AVL树的深度和og是同数量级的(其中的N为结 成,2,出现不平衡 纳点37的BF值由-1变 点个数), 成2,出现不平餐1 30 90 5/103 52/103 9.2.1-平衡二叉排序树:LL型 9.2.1-平衡二叉排序树:RR型 ,失去平堂二址二数的细生 失去平二mn 假设A山:在A结点的左孩子的左子树上 而失 假设yRR:在A结点的右孩子的右子树上 而失 去平领插入结点导致A结底失去平衡 去平仪描入结点导取A结点失去平衡 ,单向右旋平衡处理LL型 ·单向左旋平衡处理(RR型) h-1 LL RR 插入结点 53/103 54/103 合 9
2009/12/29 9 9.2.1 -二叉排序树:性能分析 二叉排序树的查找分析 与给定值比较的关键字个数不超过二叉排序树的深度 示例:从空树出发,待插的关键字序列为 33 44 23 46 12 37 二叉排序树的形态与关键字的插入次序直接相关! 如:将上例的关键字插入次序调整为: 12, 23, 33, 44, 37, 46 49/103 33,44,23,46,12,37 33 23 44 12 37 46 12 23 33 37 44 46 查找成功且各记录的查找概率相等时 ASL(a) =(1+2*2+3*3)/6=14/6 查找成功且各记录的查找概率相等时 ASL(b) =(1+2+3+4+5*2)/6=20/6 9.2.1 -二叉排序树:性能分析 二叉排序树的查找分析 平均性能:假设在含有n个关键字的序列中,i个关 键字小于第一个关键字,n-i-1个关键字大于第一个 关键字,则在n个记录的查找概率相等的情况下, 50/103 其平均查找长度为 当n≥2时, 1 Pni i Pi n i Pn i ( , ) 1 * ( ( ) 1) ( 1)( ( 1) 1) n 1 Pn n ( ) 2(1 )ln n 11 1 2 2 00 0 11 2 ( ) ( , ) 1 ( ) ( 1) ( 1) 1 ( ) nn n ii i P n P n i iP i n i P n i iP i nn n 9.2.1 -平衡二叉树:定义 平衡二叉树(AVL树, Balanced Binary Tree) 定义(递归):或者是一棵空树,或者是具有如下特性 的二叉树: 51/103 的 叉树 左子树和右子树的深度之差的绝对值不超过1; 它的左、右子树也分别是平衡二叉树。 二叉树上结点的平衡因子BF:该结点的左子树的深 度减去它的右子树的深度。 AVL树的深度和logN是同数量级的(其中的N 为结 点个数)。 根据作者姓名,Adelson-Velskii 和Landis,将 其称为AVL-树. 9.2.1 -平衡二叉排序树: 举例 如何使构成的二叉排序树成为平衡树? 示例:从空树出发,待插的关键字序列为13,24,37,90,53 13 24 24 再向左逆 向左逆时 针旋转 52/103 13 24 37 结点13的BF值由-1变 成-2,出现不平衡! 24 13 37 90 53 结点37的BF值由-1变 成-2,出现不平衡! 13 37 53 90 24 13 53 37 90 先向右顺 时针旋转 再向左逆 时针旋转 针旋转 9.2.1 -平衡二叉排序树:LL型 失去平衡后进行调整的规律 假设A是由于在二叉排序树上插入结点而失 去平衡的最小子树根结点 LL: 在A结点的左孩子的左子树上 插入结点,导致A结点失去平衡. 53/103 单向右旋平衡处理(LL型) A 2 B 1 BL BR AR 插入结点 h h-1 h-1 LL 向右顺时 针旋转 A 0 B 0 BL BR AR 9.2.1 -平衡二叉排序树:RR型 失去平衡后进行调整的规律 假设A是由于在二叉排序树上插入结点而失 去平衡的最小子树根结点 RR: 在A结点的右孩子的右子树上 插入结点,导致A结点失去平衡. 54/103 单向左旋平衡处理(RR型) h-1 A -2 B -1 BL BR AL 插入结点 h h-1 RR 向左逆时 针旋转 A 0 B 0 B BR AL L
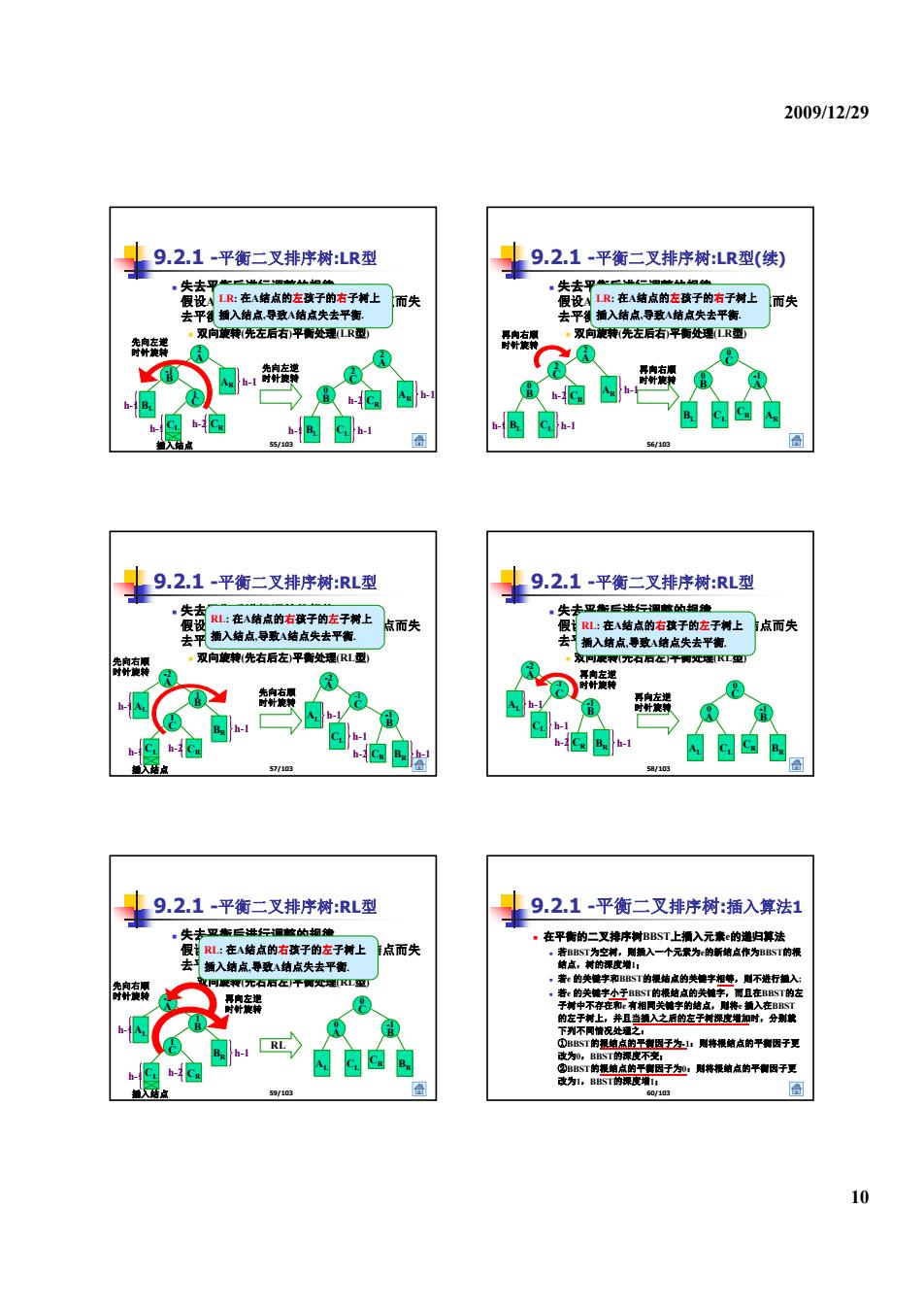
2009/12/29 9.2.1-平衡二叉排序树:LR型 9.2.1-平衡二叉排序树:LR型(续) ,失去平长二业二 失去平二二 假设AIR:在A结点的左孩子的右子树上 而失 假设R:在A结点的左孩子的右子树上 而失 去平传插入结点,导致A结点失去平衡. 去平播入结点,导致A结点失去平衡: ·双向鞭转(先左后右平衡处理(LR型) ·双向旋转(先左后右平衡处理(LR型) 先向左逆 南右 h-1 h-C h-Cg h- h-Cg b-1BL CB-1 bB. 56/103 9.2.1-平衡二叉排序树:RL型 9.2.1-平衡二叉排序树:RL型 失去 。失去亚指后#行国敏的场维 假设 RL:在A结点的右孩子的左子树上 去平插入结点,导取A结点失去平衡 点而失 假RL:在A结点的右孩子的左子树上 点而失 去平插入结点导致A结点失去平衡 先向右顺 ·双向旋转(先右后左平衡处理(RL型 双可原特(元石阿在十阿理K工里 先向右 时针转 h-V/ 再向左逆 时针旋荐 }h-1 h- h-2 h-iCa h- 入 57/103 58/103 9.2.1-平衡二叉排序树:RL型 9.2.1-平衡二叉排序树:插入算法1 ,失去卫指三进行调敏的细德 ·在平衡的二叉排序树BBST上擂入元素ε的递归算法 假RL:在A结点的右孩子的左子制上 点而失 若BBST为空满,则插入一个元素为:的新结点作为BBST的根 去 插入结点导致A结点失去平衡 结点,树的深度增1, 可眼装(元右石在平侧处理K型 着:的关幢字和BBST的根结成的关德字相尊,则不进行入: ,着e的关幢字小于BBST的根结点的关幢字,丽且在BBST的左 高左单 8 于制中不存在和有相同关铺字的结点,则将:额入在BBST 的左于树上,并且当领入之后的左子树深皮增如时,分别蝶 下列不同情况处理之: ①BBST的把地点的平腹因于左:则将根结点的平侧因子更 h-1 RL 或为加,BST的深度不变 h- h-2Cx ②BBST的根结点的平害因于如:则特根纳点的平物因子夏 改为1,BBST的深增I: 59/103 102 圄 10
2009/12/29 10 9.2.1 -平衡二叉排序树:LR型 失去平衡后进行调整的规律 假设A是由于在二叉排序树上插入结点而失 去平衡的最小子树根结点 双向旋转 先左后右 平衡处理 型 LR: 在A结点的左孩子的右子树上 插入结点,导致A结点失去平衡. 55/103 双向旋转(先左后右)平衡处理(LR型) C 1 A 2 B -1 BL CR AR h-1 h-1 h-1 CL 插入结点 h-2 先向左逆 时针旋转 A 2 C 2 BL CR B AR 0 CL h-2 h-1 h-1 h-1 先向左逆 时针旋转 9.2.1 -平衡二叉排序树:LR型(续) 失去平衡后进行调整的规律 假设A是由于在二叉排序树上插入结点而失 去平衡的最小子树根结点 双向旋转 先左后右 平衡处理 型 LR: 在A结点的左孩子的右子树上 插入结点,导致A结点失去平衡. 56/103 再向右顺 双向旋转(先左后右)平衡处理(LR型) 时针旋转 A -1 C 0 BL CR AR B 0 CL A 2 C 2 BL CR B AR 0 CL h-2 h-1 h-1 h-1 再向右顺 时针旋转 9.2.1 -平衡二叉排序树:RL型 失去平衡后进行调整的规律 假设A是由于在二叉排序树上插入结点而失 去平衡的最小子树根结点 双向旋转 先右后左 平衡处理 型 RL: 在A结点的右孩子的左子树上 插入结点,导致A结点失去平衡. 57/103 双向旋转(先右后左)平衡处理(RL型) C 1 A -2 B 1 BR CL AL h-1 h-1 h-1 CR 插入结点 h-2 先向右顺 时针旋转 先向右顺 时针旋转 B -1 C -1 AL CR BR A -2 CL h-1 h-1 h-1 h-2 9.2.1 -平衡二叉排序树:RL型 失去平衡后进行调整的规律 假设A是由于在二叉排序树上插入结点而失 去平衡的最小子树根结点 双向旋转 先右后左 平衡处理 型 RL: 在A结点的右孩子的左子树上 插入结点,导致A结点失去平衡. 58/103 B -1 C -1 AL CR BR A -2 CL h-1 h-1 h-1 h-2 双向旋转(先右后左)平衡处理(RL型) 再向左逆 时针旋转 B -1 C 0 AL CR BR A 0 CL 再向左逆 时针旋转 9.2.1 -平衡二叉排序树:RL型 失去平衡后进行调整的规律 假设A是由于在二叉排序树上插入结点而失 去平衡的最小子树根结点 双向旋转 先右后左 平衡处理 型 RL: 在A结点的右孩子的左子树上 插入结点,导致A结点失去平衡. 59/103 双向旋转(先右后左)平衡处理(RL型) RL C 1 A -2 B 1 BR CL AL h-1 h-1 h-1 CR 插入结点 h-2 先向右顺 时针旋转 再向左逆 时针旋转 B -1 C 0 AL CR BR A 0 CL 9.2.1 -平衡二叉排序树:插入算法1 在平衡的二叉排序树BBST上插入元素e的递归算法 若BBST为空树,则插入一个元素为e的新结点作为BBST的根 结点,树的深度增1; 若e 的关键字和BBST的根结点的关键字相等 则不进行插入; 60/103 若e 的关键字和BBST的根结点的关键字相等,则不进行插入; 若e 的关键字小于BBST的根结点的关键字,而且在BBST的左 子树中不存在和e 有相同关键字的结点,则将e 插入在BBST 的左子树上,并且当插入之后的左子树深度增加时,分别就 下列不同情况处理之: ①BBST的根结点的平衡因子为-1:则将根结点的平衡因子更 改为0,BBST的深度不变; ②BBST的根结点的平衡因子为0:则将根结点的平衡因子更 改为1,BBST的深度增1;