
第四章语法分析 4.1考患文法 (试说明此文法生成在符号a和b之上的所有正规表达式 ()试说明此文法是二义性的。 (©)试构造一个等价的无二义性文法,此文法给出*、连接和!等运算符号的优先级和结 合规则,有关约定见33节。 解:(a对于文法R→R'I'RIRRIR*I®ab,包含非终结符、(人a、b,由正 规表达式的定义,显然,由该文法 生的语言即相当于在字母类工=ab上的正规表达式 所表示的语言。对等于任意在符号a,b之上的正规表达式X,设X中符号◆、【(、)] 的个数共有n个。对n用归纳法证明X可由该文法生成。 1)若n=0 则X=a或X=b,可由R)a或R)b生成 2)不妨设n<=K时,X可由文法生成 则n=K+1时,若X=rs,则r,s中的运算符个数均小于等于K。 即r与s均可由文法生成。 X可由R今RTR生成。 此外,对于X=(r)或X=r*均成立 n=K+1时结论也成立。 综上所述,此文法生成在a,b之上的所有正规表达式。 (b)考虑语句b*,由此文法可得出以下两棵不同的分析树。 b* 所以,此文法是二义性的 (©)对以上所给文法消除二义性,并加以优先级及结合规则的考虑,得文法G如下: R今RTR1|R1 RI→RIR2IR2 R2→R3*|R3 显然, ,结合T优先级递减的优先级要求及以上运算的左结合规则 并且文法G无二义性,满足题中所示要求
第四章 语法分析 4.1 考虑文法 R → R’|’R | RR | R* | (R) | a | b 请注意第一个直竖是符号”或”,而不是两个候选式之间的分隔符号。 (a) 试说明此文法生成在符号 a 和 b 之上的所有正规表达式。 (b) 试说明此文法是二义性的。 (c) 试构造一个等价的无二义性文法,此文法给出*、连接和| 等运算符号的优先级和结 合规则,有关约定见 3.3 节。 解:(a) 对于文法 R → R’|’R | RR | R* | (R) | a | b,包含非终结符’|’、*、(、)、a、b,由正 规表达式的定义,显然,由该文法产生的语言即相当于在字母类∑={a, b}上的正规表达式 所表示的语言。对等于任意在符号 a,b 之上的正规表达式 X,设 X 中符号’|’、*、[(、)] 的个数共有 n 个。对 n 用归纳法证明 X 可由该文法生成。 1) 若 n=0 则 X=a 或 X=b,可由 R→a 或 R→b 生成。 2) 不妨设 n <= K 时,X 可由文法生成。 则 n=K+1 时,若 X = r | s,则 r,s 中的运算符个数均小于等于 K。 即 r 与 s 均可由文法生成。 X 可由 R → R’|’R 生成。 此外,对于 X = ( r )或 X = r*均成立 n = K+1 时结论也成立。 综上所述,此文法生成在{a, b}之上的所有正规表达式。 (b) 考虑语句 ab*,由此文法可得出以下两棵不同的分析树。 所以,此文法是二义性的。 (c) 对以上所给文法消除二义性,并加以优先级及结合规则的考虑,得文法 G’如下: R → R’|’R1 | R1 R1 → R1R2 | R2 R2 → R3* | R3 R3 → (R) | a | b 显然,此文法满足*,结合’|’优先级递减的优先级要求及以上运算的左结合规则, 并且文法 G’无二义性,满足题中所示要求。 R R R a R* b* R R * R R a b
4.2试分析下面给出的f一hen一ctse语句的文法,它的提出原本是为了矫正dangling-一tse (悬而未决的一)文法的二义性: stmtif expr then stmt matched-stmt matched-stmt if expr then matched-stmt else stmt other 试说明此文法仍然是二义性的。 解:考虑句子ifE1 then ifE2 thenS1 else ifE3 thenS2cseS3, 它具有两种如下所示的分析树: (1) matched-stmt else 则上面给出的if-then一elsc文法仍是二义性的:
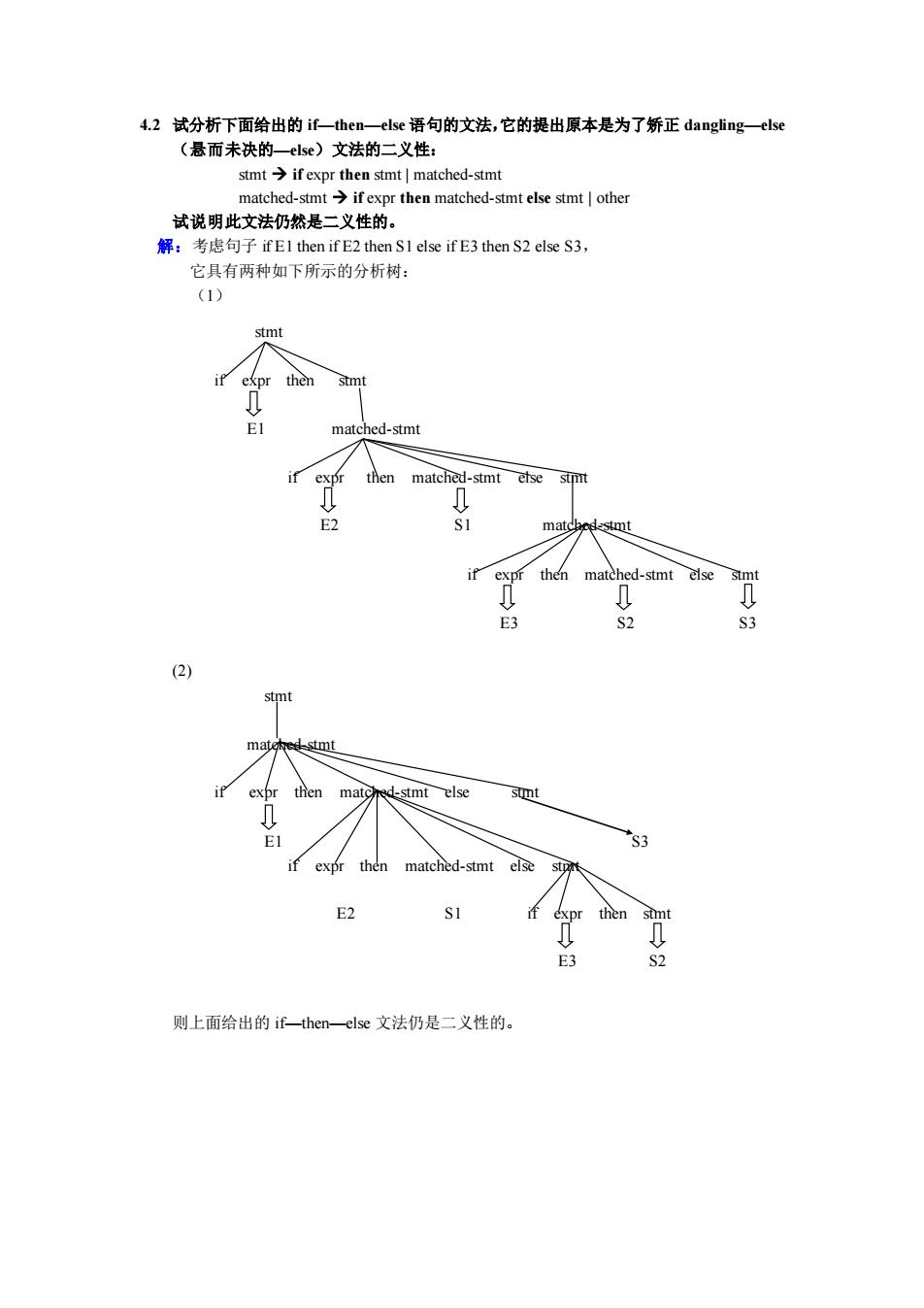
4.2 试分析下面给出的 if—then—else 语句的文法,它的提出原本是为了矫正 dangling—else (悬而未决的—else)文法的二义性: stmt → if expr then stmt | matched-stmt matched-stmt → if expr then matched-stmt else stmt | other 试说明此文法仍然是二义性的。 解:考虑句子 if E1 then if E2 then S1 else if E3 then S2 else S3, 它具有两种如下所示的分析树: (1) (2) 则上面给出的 if—then—else 文法仍是二义性的。 stmt if expr then stmt E1 matched-stmt if expr then matched-stmt else stmt E2 S1 matched-stmt if expr then matched-stmt else stmt E3 S2 S3 stmt matched-stmt if expr then matched-stmt else stmt E1 S3 if expr then matched-stmt else stmt E2 S1 if expr then stmt E3 S2

4.3对于下面的每一个语言试设计一个文法。试问其中哪些语言是正规的? 国)使得在每一个0后至立即跟随一个1的由0和1组成的符号串的全体 (e) 具有不同数目的0和1的由 0和1组成的符号串的全体 解:(a)S→0A1S1e A→IS A今1AEI0AA B→OB I0EI1B E→0E111E01e 其中(a)是正规的。 4.6试从文法s→(山川n L→LsIS 中消除左递归。并为之构造一个预测分析器。请说明句子(a(a,a》上的分析銮的动作。 解:将所给文法消除左递归得G: s→(a L→SL L→,SLIe 实现预测分析器的不含递归调用的一种有效方法是使用一张分析表和一个栈进行联合 控制,下面构造预测分析表: 根据文法G有 FIRST(s)={(,a) FOLLOW(S)={},‘,‘,e} FIRST(L)={(,a)) FOLLOW(S)= FIRSTO3)= FOLLOW(L)= 按以上结果,构造预测分析表M如下: 非终结符号 输入符号 2 S→(L) S→a L→SL' L→S 法G是)的,因为它的分析表不含多重定义入口 预测分析器对输入符号串(a(a)做出的分析动 作如 d(a. a (aa))s a.(a.a)s L→SL' a.(a.a (a.a)L→,SL (aa))s (a.a S→ S'S
4.3 对于下面的每一个语言试设计一个文法。试问其中哪些语言是正规的? (a) 使得在每一个 0 后至立即跟随一个 1 的由 0 和 1 组成的符号串的全体。 (c) 具有不同数目的 0 和 1 的由 0 和 1 组成的符号串的全体。 解:(a) S → 0A | 1S | ε A → 1S (c) S → 1A | 1E | 0AA | 0B | 0E | 1BB A → 1A | 1E | 0AA B → 0B | 0E | 1BB E → 0E1 | 1E0 | ε 其中(a)是正规的。 4.6 试从文法 S → (L) | a L → L,S | S 中消除左递归。并为之构造一个预测分析器。请说明句子(a,(a,a))上的分析器的动作。 解:将所给文法消除左递归得 G’: S → (L) | a L → SL’ L’ → ,SL’| ε 实现预测分析器的不含递归调用的一种有效方法是使用一张分析表和一个栈进行联合 控制,下面构造预测分析表: 根据文法 G’有 FIRST(s) = { ( , a ) FOLLOW(S) = { } , ‘ , ‘ , ε } FIRST(L) = { ( , a ) FOLLOW(S) = { } } FIRST(L’) = { ‘ , ‘ , ε } FOLLOW(L’) = { } } 按以上结果,构造预测分析表 M 如下: 非终结符号 输入符号 ( ) , a ε S S →( L ) S → a L L → SL’ L → SL’ L’ L’ → ε L’ → ,SL’ 文法 G’是 LL(1)的,因为它的分析表不含多重定义入口。 预测分析器对输入符号串(a, (a, a))做出的分析动作如下: 栈 输入 输出 $S (a, (a, a)) $ $)L( (a, (a, a))$ S → (L) $)L a, (a, a))$ $)L’S a, (a, a))$ L → SL’ $)L’a a, (a, a))$ S → a $)L’ , (a, a))$ $)L’S, , (a, a))$ L’ → , SL’ $)L’S (a, a))$ $)L’)L( (a, a))$ S → (L) $)L’)L a, a))$ $)L’)L’S a, a))$ L → SL’
S)LLa 5L元 L'→,SI S)L)L'a assa 4.8(a)计算下面文法GS的nuHlable,FIRST和Follow集 S→uBD B今Br|w DEF F→x )构造这个文法的山分析表 (心)给出这个文法不是LL)的证据: ()尽可能少地修玫此文法,使其成为能产生相同语言的LL()文法. 解:(a)nullable={D,E,F FIRST(S)=(u; FOLLOW(S)={e FIRST(B) FOLLOW(B)=(r,x.y) FIRST(D)=x,y, FOLLOW(D)={z FIRST(E)=v. FOLLOW(E)=xZ FIRST(Ex FOLLOW(F)=z b)该文法的L1)分析表为 非终结符厂 w SSuRD B B→B B→W D→EF F→e F→X F→e (⊙)因为MB.W有两个产生式B→Bv,B)W FIRST(Bv)=FIRST(w)={w 所以不是山 (d消除左递归即可。 S→uBDz B→wB' BrB'le D→E E=y e F=xe
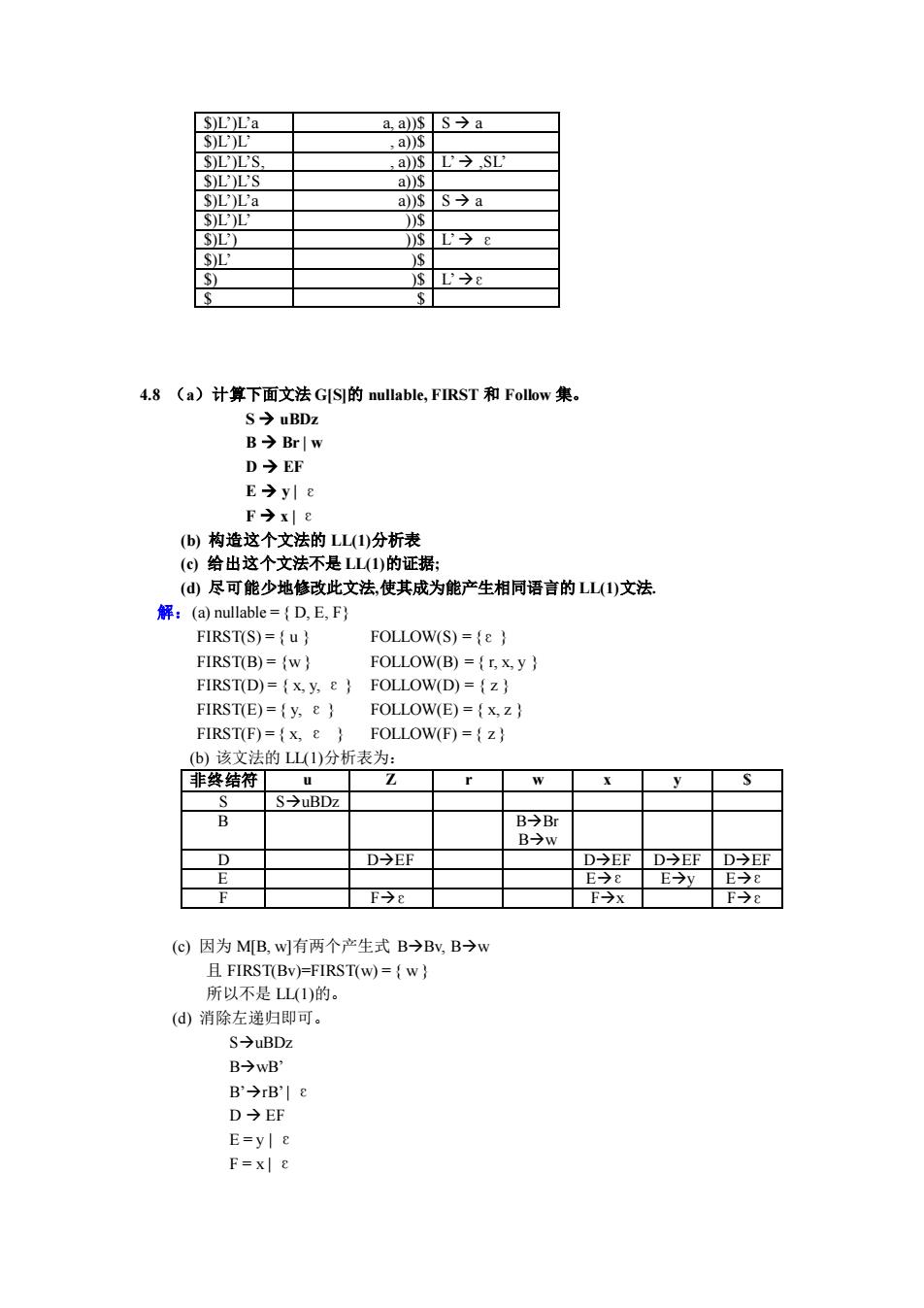
$)L’)L’a a, a))$ S → a $)L’)L’ , a))$ $)L’)L’S, , a))$ L’ → ,SL’ $)L’)L’S a))$ $)L’)L’a a))$ S → a $)L’)L’ ))$ $)L’) ))$ L’ → ε $)L’ )$ $) )$ L’ → ε $ $ 4.8 (a)计算下面文法 G[S]的 nullable, FIRST 和 Follow 集。 S → uBDz B → Br | w D → EF E → y | ε F → x | ε (b) 构造这个文法的 LL(1)分析表 (c) 给出这个文法不是 LL(1)的证据; (d) 尽可能少地修改此文法,使其成为能产生相同语言的 LL(1)文法. 解:(a) nullable = { D, E, F} FIRST(S) = { u } FOLLOW(S) = { ε } FIRST(B) = {w } FOLLOW(B) = { r, x, y } FIRST(D) = { x, y, ε } FOLLOW(D) = { z } FIRST(E) = { y, ε } FOLLOW(E) = { x, z } FIRST(F) = { x, ε } FOLLOW(F) = { z } (b) 该文法的 LL(1)分析表为: 非终结符 u Z r w x y $ S S→uBDz B B→Br B→w D D→EF D→EF D→EF D→EF E E→ ε E→y E→ ε F F→ ε F→x F→ ε (c) 因为 M[B, w]有两个产生式 B→Bv, B→w 且 FIRST(Bv)=FIRST(w) = { w } 所以不是 LL(1)的。 (d) 消除左递归即可。 S→uBDz B→wB’ B’→rB’| ε D → EF E = y | ε F = x | ε