补充题:写出下列语言的上下文无关文法 (a){abab"1n,m≥0} G-({a,b1,{S,A,B;,Sm) T:SAB:A→aAbE:B→aBbe b){10101n,m≥0} G-{1,03,{S,A},S,m I:S1A0IAE:A→0A1IE (d{oco1o∈{a,b}} G({ab,c,s,S,⑩ T:s→aSa|bSb|8 (心)不以0开始的奇数集 G{1,2,3,45,67,89,0+,s,UE}S, 正:S+U-UIU:U→AEE:E1I357I9:AA01A1A2IA3lA9123.9 1.1 (b)分析树 ()a,a (a,(aa)
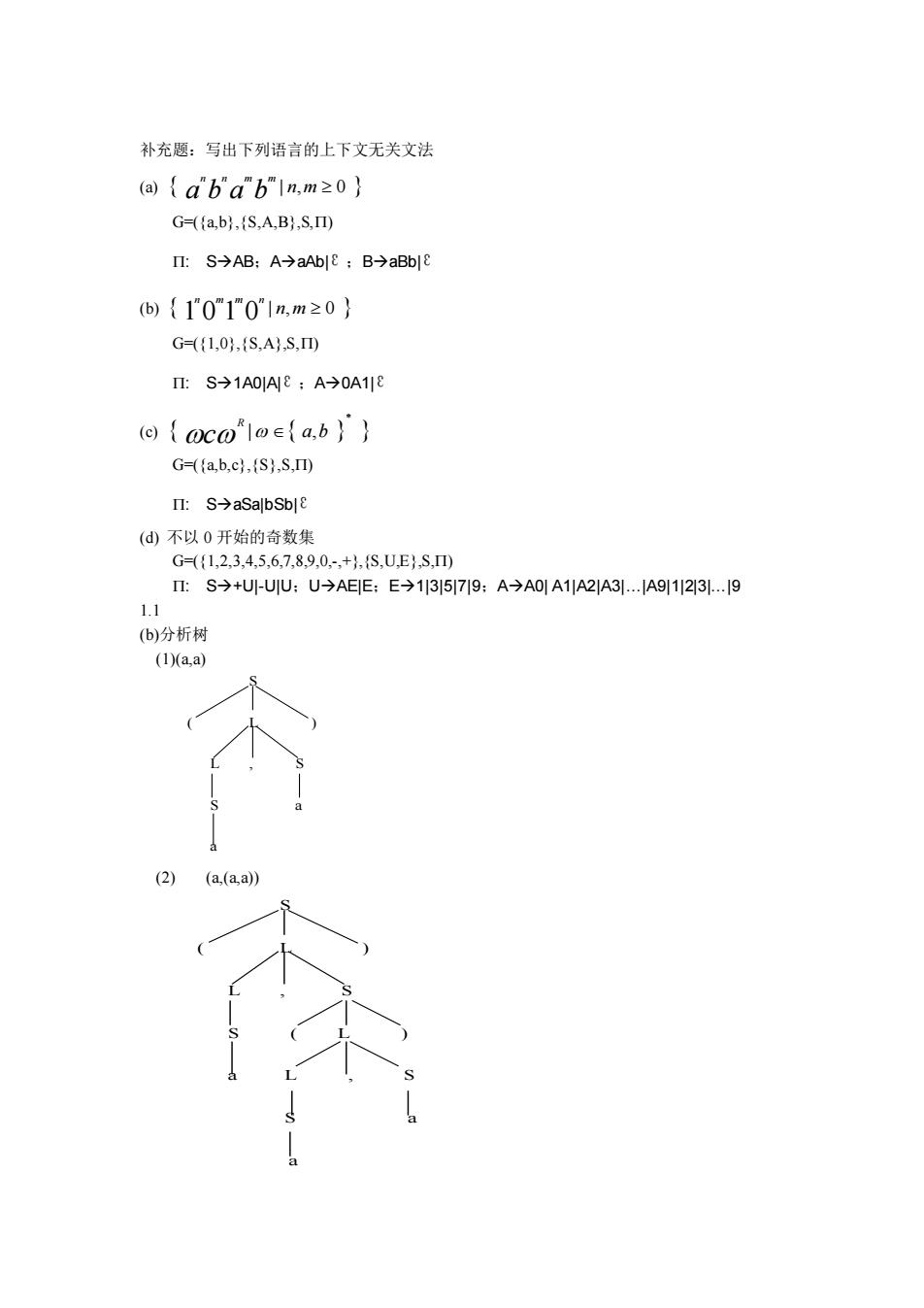
补充题:写出下列语言的上下文无关文法 (a) a b a b | n,m 0 n n m m G=({a,b},{S,A,B},S,) : S→AB;A→aAb| ε ;B→aBb| ε (b) 1 0 1 0 | n,m 0 n m m n G=({1,0},{S,A},S,) : S→1A0|A| ε ;A→0A1| ε (c) c a b R | , G=({a,b,c},{S},S,) : S→aSa|bSb| ε (d) 不以 0 开始的奇数集 G=({1,2,3,4,5,6,7,8,9,0,-,+},{S,U,E},S,) : S→+U|-U|U;U→AE|E;E→1|3|5|7|9;A→A0| A1|A2|A3|.|A9|1|2|3|.|9 1.1 (b)分析树 (1)(a,a) S ( L ) L , S S a a (2) (a,(a,a)) S ( L ) L , S S ( L ) a L , S S a a
(3(a(aa.(aa ()最左推导 (I)S(L)→L,S)S,S)(aS)→(aa) (2)S→() 短语:() 直接短语:() →LS) LS/(LS)) LS (ss) SIS.SI(S.S) →(aS) ala.Sl(aS) →(a(L) al(L)la.L)l(a(L)】 al(L) (a(LS)) alLSIS)la(LS)I(a(LS)) alLS →(S.(S.S) alSI S.SI(S.S)la(S.S)(a(S.S)) als (a(a S)) ala sla s)lala s)l(a(a s)) →(a(aa》 aIa.al(a.a)Ia.(a.a)I(a.(a.a)) (3)S→)→L,S)→S,S)→(aS)→(a,L》→(aL,S)→(a,(S,S》→(a().S →(a(LS),S)→(a,(sS),S)→(a(a,S,S)→(a,(aa,S)→(a(a,a(L)) (a((a.a)(LS)))(a((aa)(S.S))(a((aa).(a.S)))(a((aa)(aa))) (d最右推导 ((sa(aa) (②)SL)→LS)→LL》→L(L,S)→L(La)→L(S.a)→L(a,a)→S,(aa →(a(aa) (3)SL)→L,S)→L(L)→(L(LS)→L,(L(L》)→L,(LL,S)→L(L).L,a)→ (L(L(S.a)))L(L(aa))(L(S.(aa)))(L((L)(aa)))(L(LS)(aa)) L,(L,a.(aa》→(L(s,a.aa》→(L,(aaaa》→(S,(aa.(aa》→a((aa)(aa》 (e)生成语言 以a为基本元素构成的广义表 1.2 (a)最左推导 S→asbs→abSaSbS.→abaSbS>ababs abab
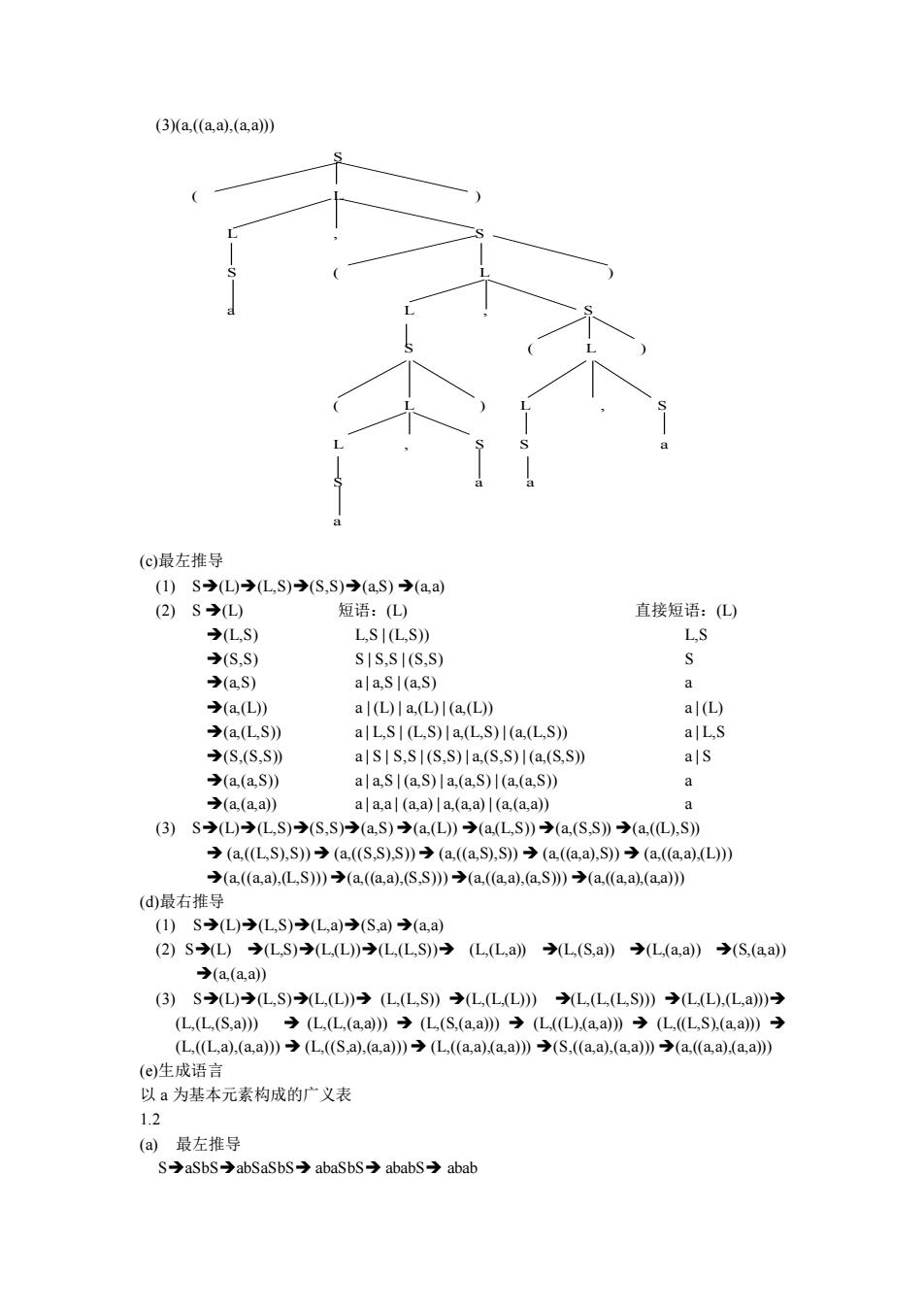
(3)(a,((a,a),(a,a))) S ( L ) L , S S ( L ) a L , S S ( L ) ( L ) L , S L , S S a S a a a (c)最左推导 (1) S➔(L)➔(L,S)➔(S,S)➔(a,S) ➔(a,a) (2) S ➔(L) 短语:(L) 直接短语:(L) ➔(L,S) L,S | (L,S)) L,S ➔(S,S) S | S,S | (S,S) S ➔(a,S) a | a,S | (a,S) a ➔(a,(L)) a | (L) | a,(L) | (a,(L)) a | (L) ➔(a,(L,S)) a | L,S | (L,S) | a,(L,S) | (a,(L,S)) a | L,S ➔(S,(S,S)) a | S | S,S | (S,S) | a,(S,S) | (a,(S,S)) a | S ➔(a,(a,S)) a | a,S | (a,S) | a,(a,S) | (a,(a,S)) a ➔(a,(a,a)) a | a,a | (a,a) | a,(a,a) | (a,(a,a)) a (3) S➔(L)➔(L,S)➔(S,S)➔(a,S) ➔(a,(L)) ➔(a,(L,S)) ➔(a,(S,S)) ➔(a,((L),S)) ➔ (a,((L,S),S)) ➔ (a,((S,S),S)) ➔ (a,((a,S),S)) ➔ (a,((a,a),S)) ➔ (a,((a,a),(L))) ➔(a,((a,a),(L,S))) ➔(a,((a,a),(S,S))) ➔(a,((a,a),(a,S))) ➔(a,((a,a),(a,a))) (d)最右推导 (1) S➔(L)➔(L,S)➔(L,a)➔(S,a) ➔(a,a) (2) S➔(L) ➔(L,S)➔(L,(L))➔(L,(L,S))➔ (L,(L,a)) ➔(L,(S,a)) ➔(L,(a,a)) ➔(S,(a,a)) ➔(a,(a,a)) (3) S➔(L)➔(L,S)➔(L,(L))➔ (L,(L,S)) ➔(L,(L,(L))) ➔(L,(L,(L,S))) ➔(L,(L),(L,a)))➔ (L,(L,(S,a))) ➔ (L,(L,(a,a))) ➔ (L,(S,(a,a))) ➔ (L,((L),(a,a))) ➔ (L,((L,S),(a,a))) ➔ (L,((L,a),(a,a))) ➔ (L,((S,a),(a,a)))➔ (L,((a,a),(a,a))) ➔(S,((a,a),(a,a))) ➔(a,((a,a),(a,a))) (e)生成语言 以 a 为基本元素构成的广义表 1.2 (a) 最左推导 S➔aSbS➔abSaSbS➔ abaSbS➔ ababS➔ abab
S→asbs→abS>abaSbS ababs>abab 故文法是二义性的。 (句)最右推导 s→asbs→aSbaSbS-→aSbaSb→aSbab>abab s→asbs→aSb>abSaSb→abSab>abab (⊙分析树 (1) (2) (d生成语言 由字母ab构成且ab个数相等的字符串组成的集合。 1.3b)分析树 bfacto faise 补充题1:写出下列语言的三型文法 (a{a1n20} G-((a).{S)S.I) Π:S→asIe (b){ab"1n,m21}
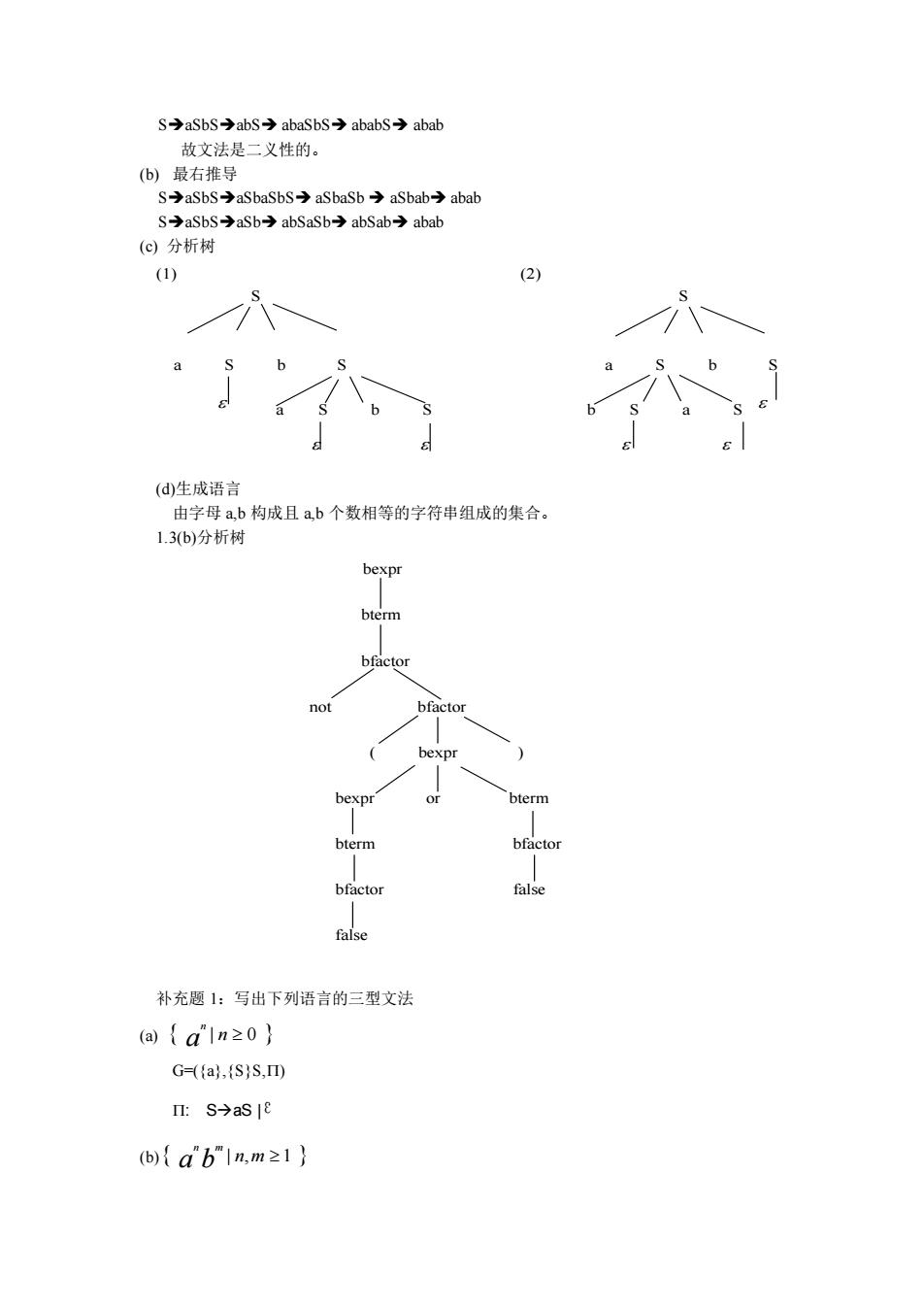
S➔aSbS➔abS➔ abaSbS➔ ababS➔ abab 故文法是二义性的。 (b) 最右推导 S➔aSbS➔aSbaSbS➔ aSbaSb ➔ aSbab➔ abab S➔aSbS➔aSb➔ abSaSb➔ abSab➔ abab (c) 分析树 (1) (2) S S a S b S a S b S a S b S b S a S (d)生成语言 由字母 a,b 构成且 a,b 个数相等的字符串组成的集合。 1.3(b)分析树 bexpr bterm bfactor not bfactor ( bexpr ) bexpr or bterm bterm bfactor bfactor false false 补充题 1:写出下列语言的三型文法 (a) a | n 0 n G=({a},{S}S,) : S→aS | ε (b) a b | n,m 1 n m

G=fab}.fS.B;S.Π) :SaSaB:B→blbB (@{ab"c1n,m,k≥1} G-((a.b.cJ.(S.B.C).S.I) m:S→aSaB:B→bBbC:C→ccC (d)PASCAL的标识符 G-(f01.9.a.b.AB.(D.LDj.ID.I) IT:IDaLD|bLD.zLDJALD|BLD.ZLD LD>aLD]bLD.zLDIALD]BLD.|ZLDJOLD]1LDI.J9LD8 (e)PASCAL.整数 G-0,19+,U,Cs, 正S→0-Uj+UU U→1C2Cl.l9C 补充题2:己知文法G其产生式如下:S→(S£ (a)L(GSD是什么? (b)对于(a)的结果,请给出证明 (a)解:L(GS={)1n≥0} b)证明: 1:首先证明L(GSc{)°1n20} 对推导次数进行归纳 1)当推导次数为1时,使用产生式S)£,此时左括号与右括号个数为0 2):假设推导次数为n时(a)成立,即 S>(S)》=>(》 则推导次数为n+1次时,多使用一次产生式S→(S)即 s((S》->((S》=>((》 推导次数为n+1次时(a)成立。 根据(1)(2)可得:L(GSc{()°1n之0} 2:其次证明{)°1n≥0}cL(GS 对n进行归纳 1)当n=0时,使用产生式S)£即可
G=({a,b},{S,B},S,) : S→aS|aB;B→b|bB (c) a b c | n,m, k 1 n m k G=({a,b,c},{S,B,C},S,) : S→aS|aB;B→bB|bC;C→c|cC (d) PASCAL 的标识符 G=({0,1,.9,a,b,.z,A,B,.Z},{ID,LD},ID, ) : ID→aLD|bLD.zLD|ALD|BLD.|ZLD LD→ aLD|bLD.zLD|ALD|BLD.|ZLD|0LD|1LD|.|9LD| ε (e)PASCAL 整数 G=({0,1,.9,-,+},{S,U,C},S, ) : S→0|-U|+U|U U→1C|2C|.|9C| C→0C|U| ε 补充题 2:已知文法 G[S],其产生式如下:S→(S)| ε (a)L(G[S])是什么? (b)对于(a)的结果,请给出证明 (a) 解:L(G[S])= ( ) | n 0 n n (b)证明: 1:首先证明 L(G[S]) ( ) | n 0 n n 对推导次数进行归纳 1):当推导次数为 1 时,使用产生式 S→ ε ,此时左括号与右括号个数为 0 2):假设推导次数为 n 时(a)成立,即: S (((. .))) −1 −1 + == n n S (((.))) −1 −1 == n n 则推导次数为 n+1 次时,多使用一次产生式 S→(S)即: S (((. .))) −1 −1 + == n n S (((. .))) n n == S (((.))) n n == 推导次数为 n+1 次时(a)成立。 根据(1)(2)可得:L(G[S]) ( ) | n 0 n n 2:其次证明 ( ) | n 0 n n L(G[S]) 对 n 进行归纳 1):当 n=0 时,使用产生式 S→ ε 即可;

2):假设当nk时,结论成立,即()∈L(GSD,下面证n=k+1时结论成立。 由∈L(GS,其推导过程如下: 5>(.S.》=>(《(》 当n=k+1时,推导过程如下 s(.S.》=((.S.》=>((.》 故)∈L(GS 根据(1)(2)可得:{()°1n≥0}cL(GS 根据1,2可知:L(GS={)"1n≥0}
2):假设当 n=k 时,结论成立,即 ( ) k k L(G[S]),下面证 n=k+1 时结论成立。 由 ( ) k k L(G[S]),其推导过程如下: S (((. .))) k k S + == (((.))) k k == 当 n=k+1 时,推导过程如下: S (((. .))) k k S + == (((. .))) +1 +1 == k k S (((.))) +1 +1 == k k 故 + + ( ) k 1 k 1 L(G[S]) 根据(1)(2)可得: ( ) | n 0 n n L(G[S]) 根据 1,2 可知:L(G[S])= ( ) | n 0 n n