③#与其它终结符的关系:(相当于加了一条产生式S”一#S#) a#·文法所有句型的头终结符(含()一非终结符开头的情况)即##,即LASTVT(S)·>≥# 例1P103S→#S# 例2①=·:(=)#=·# ②ii{i,a,)J LASTVT(D) ·( a,) () {a,)} +) i.a.)1 .FIRSTVT(S)=i.a. LASTVT(T)·>+ {+,i.a,)} LASTVT(S)·># 构造优先关系表: i a <。 < <· < < < = 其中空格表示错误关系,报错如果表中没有一个单元格有两种优先关系则说明文法是算符 优先文法 四素短语:P110 是一个短语,包含至少一个终结符,除自身不包含其它素短语 例1P110
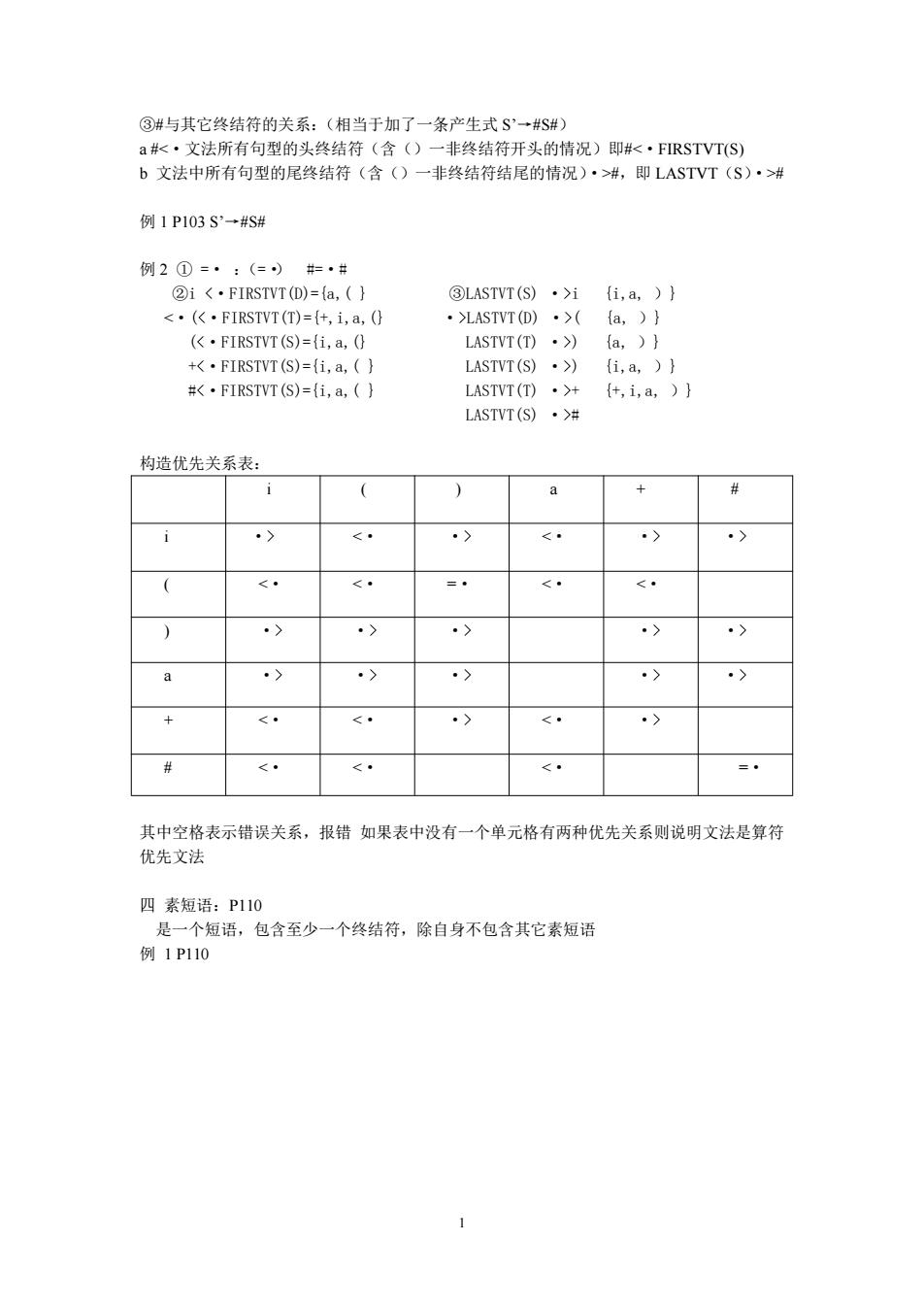
1 ③#与其它终结符的关系:(相当于加了一条产生式 S’→#S#) a ##,即 LASTVT(S)·># 例 1 P103 S’→#S# 例 2 ① =· :(=·) #=·# ②i i {i,a, )} LASTVT(D) ·>( {a, )} () {a, )} +) {i,a, )} #+ {+,i,a, )} LASTVT(S) ·># 构造优先关系表: i ( ) a + # i ·> ·> ( ·> ·> ·> ·> a ·> ·> ·> ·> ·> + # <· <· <· =· 其中空格表示错误关系,报错 如果表中没有一个单元格有两种优先关系则说明文法是算符 优先文法 四 素短语:P110 是一个短语,包含至少一个终结符,除自身不包含其它素短语 例 1 P110

例2.GE]E一>E+TTT->T*FFF->P+FPP->E)M看符号串P*P+i是否是合法句 EE+T-E+F->E+P->E+i=>T+i-T*F+iTP+i=>F*P+iP+P+i 短语:PP+i(E) 简单短语: 素短语:Pp P+P(E,T) PI(F) PI(E,T) P2(F) 最左素短语: P2(F) i(P) p*P i(P.F.T) 句柄P1(F p :算符优先文法可看非终结符,“最左素短语就相当于原来的句柄,即先规约最左素短语。 P111.优先关系决定最左素短语。 五.算符优先分析算法:设GS-(Vn,VPS)为算符优先文法 (1)由文法G(S)构造优先关系矩阵。 (2)设置一个符号栈S。存放已规约的或待形成最左素短语的符号串,另设一个工作单元 R,存放当前的待输入符号。 (3)用移进一规约的方法,当符号栈S的栈顶形成不规约串一最左素短语时,进行规约, 耳体方法加下: ①分析开始时,S中只有一个符号“#”,R中存放输入串(源程序)的第一个终结符 ②查优先关系矩阵,比较符号栈中最靠栈顶的终结符(假设为)与R中的终结符(假设为 b)的优先关系: )若a,b之间无优先关系,则出错并退出分析程序。 ii) 若a<·b或a=·b,则将b进栈,指针后移,R中存放下一个待输入终结符,重复 若a·b,则表明此时栈项已形成最左素短语(且其右界已空)转③ ③.从S中普栈顶的终结符X开始,依次向前(向栈底方向)与最远 的终结符比较,若Xn1=Xa,则继续比较X2和X1,如比较反复, 直至X<X,(i=l,2,.,n设X-#)为止。 于是最左来短语的左界已确定,此时最古来短语为从N:开始(N:为 在X之前临X的非终结符,若为N=e,则从X开始)一直到找顶 的符号串:Ni、X、N+I、X+I、Nn、Xn、Nn+1. 2
2 例 2. G[E]:E->E+T/T T->T*F/F F->P+F/P P->(E)/I 看符号串 P*P+i 是否是合法句 型。 E=>E+T=>E+F=>E+P=>E+i=>T+i=>T*F+i=>T*P+i=>F*P+i=>P*P+i E 短语:P*P+i(E) 简单短语: 素短语:P*P P*P(E,T) P1(F) i E + T P1(F,T) P2(F) 最左素短语: P2(F) i(P) P*P T F i(P,F,T) 句柄 P1(F) T * F P F P2 i P1 ∵算符优先文法可看非终结符,∴最左素短语就相当于原来的句柄,即先规约最左素短语。 P111. 优先关系决定最左素短语。 五. 算符优先分析算法:设 G[S]=(Vn,Vt,P,S)为算符优先文法 (1)由文法 G(S)构造优先关系矩阵。 (2)设置一个符号栈 S。存放已规约的或待形成最左素短语的符号串,另设一个工作单元 R,存放当前的待输入符号。 (3)用移进—规约的方法,当符号栈 S 的栈顶形成不规约串—最左素短语时,进行规约, 具体方法如下: ①分析开始时,S 中只有一个符号“#”,R 中存放输入串(源程序)的第一个终结符。 ②查优先关系矩阵,比较符号栈中最靠栈顶的终结符(假设为 a)与 R 中的终结符(假设为 b)的优先关系: i) 若 a,b 之间无优先关系,则出错并退出分析程序。 ii) 若 ab,则表明此时栈顶已形成最左素短语(且其右界已空)转③ ③.从 S 中普栈顶的终结符 Xn开始,依次向前(向栈底方向)与最远 的终结符比较,若 Xn-1=Xn,则继续比较 Xn-2 和 Xn-1,如比较反复, 直至 Xi-1<Xi,(i=1,2,.,n 设 X0=#)为止。 于是最左来短语的左界已确定,此时最古来短语为从 Ni 开始(Ni 为 在 Xi之前临 Xi的非终结符,若为 Ni=ε,则从 Xi开始)一直到找顶 的符号串:Ni、Xi、Ni+1、Xi+1、.Nn、Xn、Nn+1

④.文法G[S]的产生式集中,选择其右P具有NXN+1Xi.NnXaNnt! 形式的规则进行归约(注意:此时非终结符号不必完全相同):弹击 符号栈栈顶的最左来短语相应规则的左部非终结进栈,若此时分析栈 中只有#和文法的一个非终结符,且待分析符号串只剩#(即R中符 号为#),则表明分析成功,所分析的串是文法句子退出分析程序:否 则,重复②。 例1、Po,表6.8 例2、G[S]:S→D(R)IDR-→R:P|PP→S|iD→i分析i(i: i) D FIRSTUT (S)=(()UFIRSTUT (D)=((,i) FIRSTUT (R)=(;}UFIRSTUT (P)=(;,(i) FIRSTUT (P)=FIRSTUT (S)U(i)=((,i) FIRSTUT (D)=(i) LASTUT (S)=())ULASTUT (D)=(),i) LASTUT (R)=(;ULASTUT (P)=(:,i, LASTUT (R)=(i)ULASTUT (S)=(i,) LASTUT(D)=【i) ②加一条S'→#S# (=)#=#一(K·F1 RSTUT(R) LASTUT(D)·>( : LASTUT(R)·>) #·F1 RSTUT(S) LASTUT(R)·>: LASTUT(R)·>#
3 ④.文法 G[S]的产生式集中,选择其右 P 具有 NiXiNi+1Xi+1.NnXnNn+1 形式的规则进行归约(注意:此时非终结符号不必完全相同):弹击 符号栈栈顶的最左来短语相应规则的左部非终结进栈,若此时分析栈 中只有#和文法的一个非终结符,且待分析符号串只剩#(即 R 中符 号为#),则表明分析成功,所分析的串是文法句子退出分析程序;否 则,重复②。 例 1、P110,表 6.8 例 2、G[S]:S→D(R)|DR→R;P|P P→S|i D→i 分析 i(i; i) 1 F1RST∪T(S)=﹛(﹜∪FIRST∪T(D)=﹛(,i﹜ F1RST∪T(R)=﹛;﹜∪FIRST∪T(P)=﹛;,(,i﹜ F1RST∪T(P)= FIRST∪T(S)∪﹛i﹜=﹛(,i﹜ FIRST∪T(D)=﹛i﹜ LAST∪T(S)=﹛)﹜∪LAST∪T(D)=﹛), i﹜ LAST∪T(R)=﹛;﹜∪LAST∪T(P)=﹛;, i,)﹜ LAST∪T(R)=﹛i﹜∪LAST∪T(S)=﹛i,)﹜ LAST∪T(D)=﹛i﹜ 2 加一条 S'→# S # (=) # = # (( LAST∪T(R)·>) #; LAST∪T(R)·>#
( i # ( ·> 。> ·> ·> ·> 。> 。> 。> ∴此文法是算符优先文法。 ③步骤 符号栈输入串 iii)# 2 #i (i:i# i·>(#j(〈·Ii归约 6 #P(P ;i)# (K·j #P(P, i)# #粗(P;i )#i·)j〈·i∴.i归约 9 #P (P.P )#j·>)(《·jP;P归约 10 #P(R )#(曰) #P(R) )·>#,(=),#K·(.∴(R)归约 12 ∴.此串是文法的句子 判断i是否句子
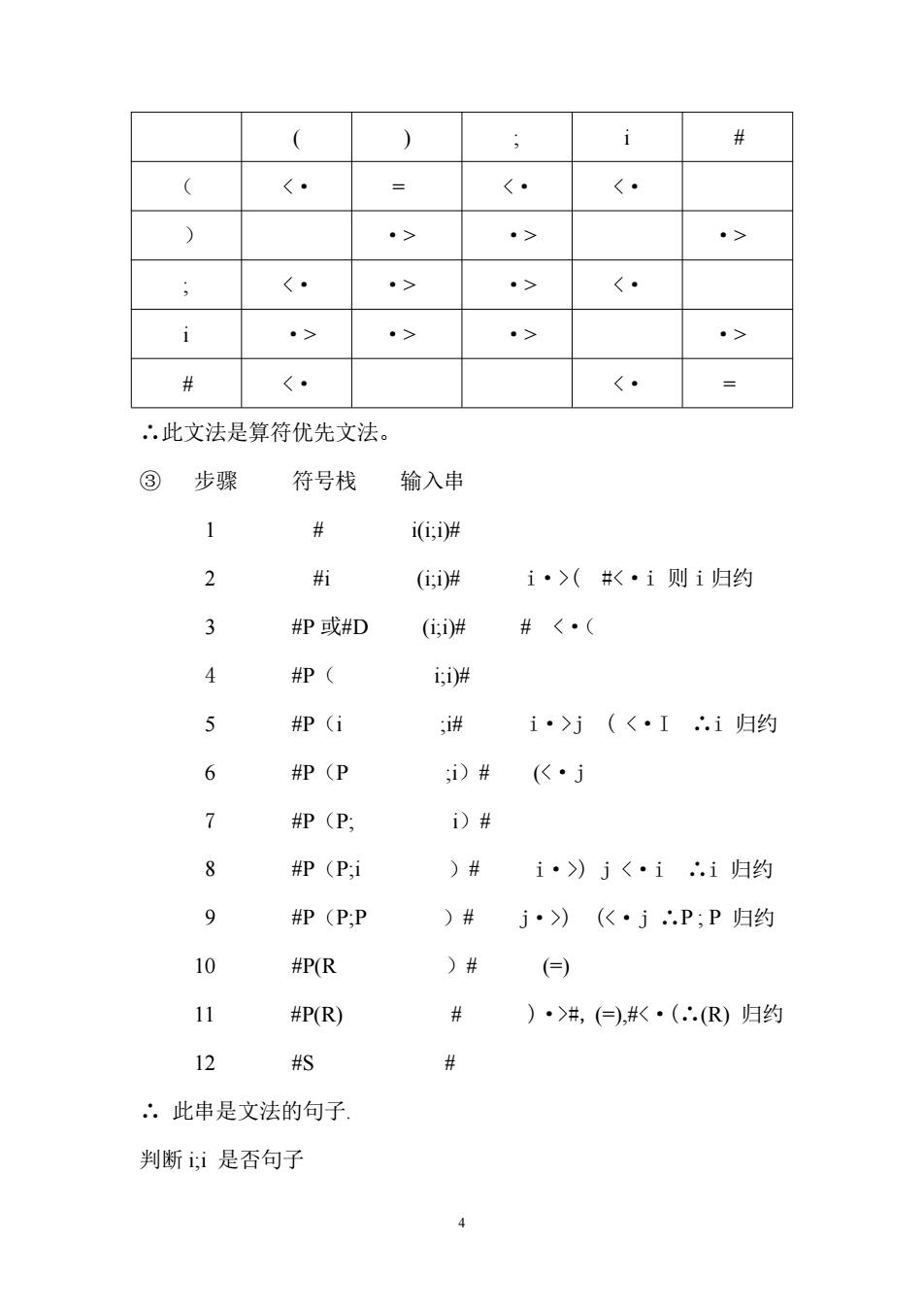
4 ( ) ; i # ( ·> ·> ; ·> ·> ·> ·> # ( #j ( ) j ) (#, (=),#<·(∴(R) 归约 12 #S # ∴ 此串是文法的句子. 判断 i;i 是否句子

i讲 2 #i ;讲 i·>:#<·ii归约 3 #P 经 #与,无关.Error .此串不是文法的句子 实验: 实验一:源程序例表程序 任意读一程序,结果加行号,若超过多少行,加页号,显示标题,日期, 时间 实验二:简单记号扫描程序 简单记号(单词):单词(全由字母组成)、数(全由数字组成)、句点。 结果显示为二元式 实验三:源代码压缩程序 回车,换行,Tb等多余字符都去掉,其中用空格区分 实验四:扫描器 区分的单词,包括保留字等。 第六章LR(K)分析法 P17,LR自底向上规范归约,不带回溯,准确,每步都是对当 前句型找句柄。 L:从左到右扫描。R:最右推导的逆过程.K:向前看的符号数大 多数上下文无关文法(二型文法)都是LR类文法,对文法的限制少, 但同时对它的分析也相应最复杂
5 1 # i;i# 2 #i ;i# i·>; #<·i ∴i 归约 3 #P ;i# #与; 无关. Error ∴ 此串不是文法的句子. 实验: 实验一: 源程序例表程序 任意读一程序,结果加行号,若超过多少行,加页号,显示标题,日期, 时间 实验二: 简单记号扫描程序 简单记号(单词): 单词(全由字母组成)、数(全由数字组成)、句点。 结果显示为二元式 实验三: 源代码压缩程序 回车,换行,Tab 等多余字符都去掉,其中用空格区分 实验四: 扫描器 区分的单词,包括保留字等。 第六章 LR(K)分析法 P117. LR 自底向上 规范归约,不带回溯,准确,每步都是对当 前句型找句柄。 L:从左到右扫描. R:最右推导的逆过程. K:向前看的符号数大 多数上下文无关文法(二型文法)都是 LR 类文法,对文法的限制少, 但同时对它的分析也相应最复杂

1、LR(0):最简单,对文法的限制多,所以多数文法都不是LR(0) 2、SLR(1):S简单,向前看一个符号,实现容易,有使用价值。 3、LR(1):多数二型文法都是LR(1),能力最强,分析表体积大, 占用空间大,代价高。 4、LALR(1):适用文法广,可以解决SLR(1)解决不了的问题, 同时也克服LR(1)存储容易过大的缺点。 §6.1LR分析概述 §6.2LR(0)分析 前缀:任意首部.例abc的前缀:e,a,ab,abc. 活前缀:如符号串为规范句型,则它的前缀叫活前缀。 一.R(0)项目:P125 例:GS']S'→SS→(S)SS→e S'→.SS→.(S)SS→.(8个项目) S'→S.S→(.S)S S→(S.)S S→(S).S S→(S)S. 项目分类P17 移进项目A一a.aB 归约项目A→a. 待归约项目A→a.BB
6 1、LR(0):最简单,对文法的限制多,所以多数文法都不是 LR(0) 2、SLR(1):S 简单,向前看一个符号,实现容易,有使用价值。 3、LR(1):多数二型文法都是 LR(1),能力最强,分析表体积大, 占用空间大,代价高。 4、LALR(1):适用文法广,可以解决 SLR(1)解决不了的问题, 同时也克服 LR(1)存储容易过大的缺点。 §6.1 LR 分析概述 §6.2 LR(0)分析 前缀:任意首部. 例 abc 的前缀:ε,a ,ab,abc. 活前缀:如符号串为规范句型,则它的前缀叫活前缀。 一.LR(0)项目:P125 例:G[S′] S′→S S→(S)S S→ε S′→.S S→.(S)S S →. (8 个项目) S′→S. S→(.S)S S→(S.)S S→(S).S S→(S)S. 项目分类 P127 移进项目 A→α.aβ 归约项目 A→α. 待归约项目 A→α.Bβ

接受项目S→a, 二.LR(0)项目集规范族P127、P129 1.G[S]:S-aAcBe A-b A-Ab B-d 先加拓广S'→S s'+s. -.aAcB aAcB.e -aAcBe. →AE LR(O)项目集规范族,识别活前缀的DFA 活前缀从初态出发,经过前弧上的所有符号到任何一个终态,I,是 句子的终态。 移进一归约冲突)不是LR(0)文法。 归约一归约冲突 三.分析表的构造P130
7 接受项目 S→α. 二.LR(0)项目集规范族 P127 ~ P129 例 1.G[S]: S→aAcBe A→b A→Ab B→d 先加拓广 S'→S I0 S'→.S S→.aAcBe I2 S→a.AcBe A→.b A→.Ab A→b. I1 S'→S. I3 S→aA.cBe A→A.b I5 S→aAc.Be B→.d I9 S→aAcBe. a b S A I8 S→aAcB.e c B e I6 A→Ab. I7 B→d. b d LR(0)项目集规范族,识别活前缀的 DFA 活前缀从初态出发,经过前弧上的所有符号到任何一个终态,I1是 句子的终态。 移进—归约冲突 不是 LR(0)文法。 归约—归约冲突 三.分析表的构造 P130
简单讲:C“.”遇到终结符,移进S,i为下一个状态 “.”左最后,归约r.归约时,所有终结符都归约.LR (0)不向前看. “.”遇非终结符.goto[k.A]为j. 例P表7.3 四,LR(O)分析器的工作过程P 例1:(0)A'→A (1)A→(A) (2)A+a判断是否为 LR(O)文法,并分析串#(a)#是否为句子. N 6 A'A A'→A A(A) A A-a ,A→(A) A-.(A) A→(A) A→(A) A-.a 6 A→a 状态 ACTION GOTO a A 0 S2 1 1 acc 2 S2 4 r2
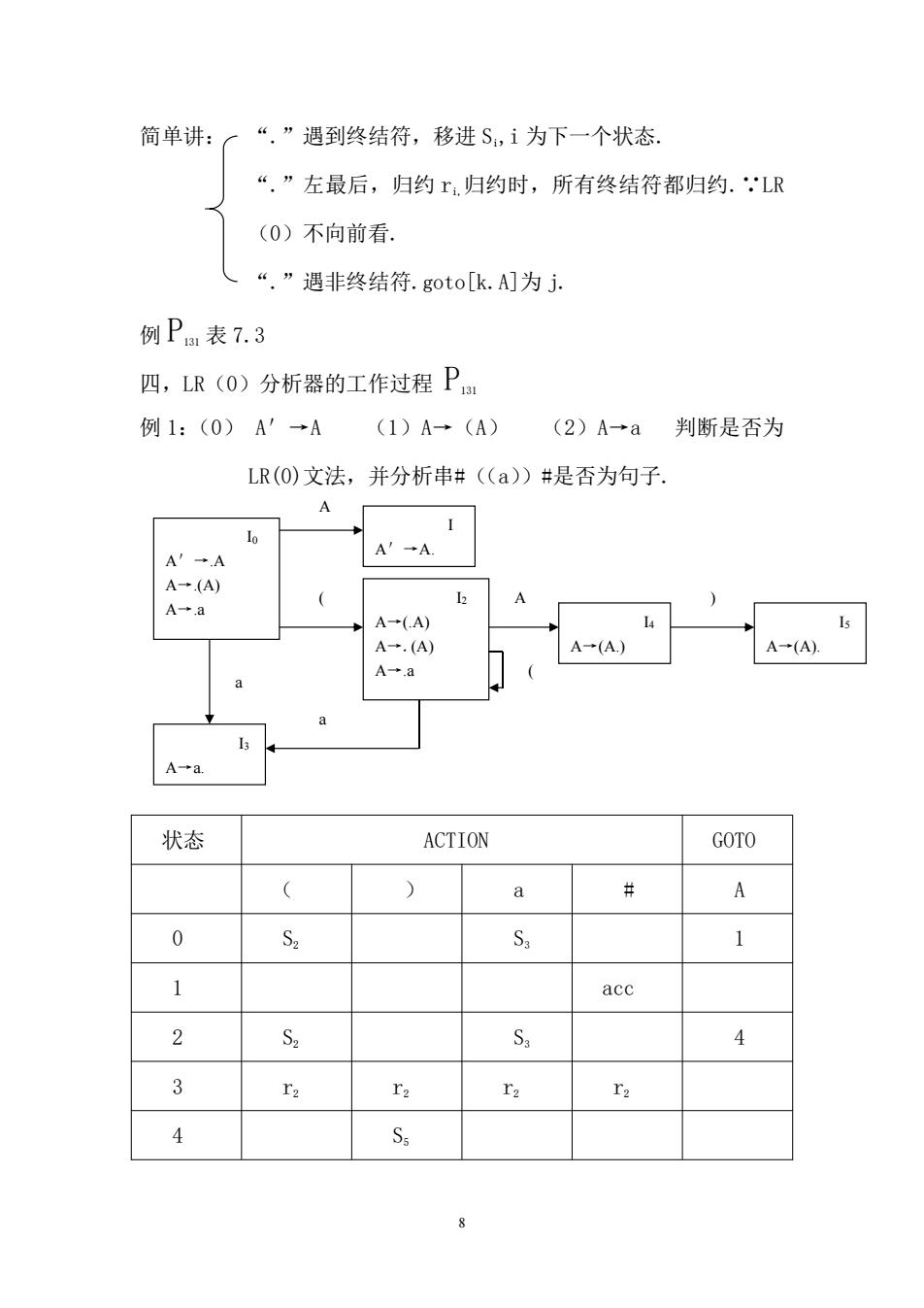
8 简单讲: “.”遇到终结符,移进 Si,i 为下一个状态. “.”左最后,归约 ri,归约时,所有终结符都归约.∵LR (0)不向前看. “.”遇非终结符.goto[k.A]为 j. 例 P131 表 7.3 四,LR(0)分析器的工作过程 P131 例 1:(0) A'→A (1)A→(A) (2)A→a 判断是否为 LR(0)文法,并分析串#((a))#是否为句子. I0 A'→.A A→.(A) A→.a I A'→A. I2 A→(.A) A→.(A) A→.a ( I4 A→(A.) I5 A→(A). A ) ( I3 A→a. a a 状态 ACTION GOTO ( ) a # A 0 S2 S3 1 1 acc 2 S2 S3 4 3 r2 r2 r2 r2 4 S5 A

51 r 空白处为error.∴.此文法是LR(O)文法没有移一归或归一归 冲突, 步骤 状态栈 符号栈 输入串 1 0 (a)# 2 02 #( (a)# 3 022 #( a))# 0223 #(a )# 5 0224 #(A )# 6 02245 #(A) )# 7 024 #(A )# 8 0245 #A) 9 01 #A #acc ∴此串为文法的句子」 例2GEJ:(O)E'一E()E→E+n (2)E-n E-n E-n 其中1中规约一移进冲突.不是LR(0)文法 例3G[A]O)A→A(1)A→aAd(2)A→aAb(3)A一E 9
9 5 r1 r1 r1 r1 空白处为 error. ∴此文法是 LR(0)文法 ∵没有移—归或归—归 冲突. 步骤 状态栈 符号栈 输入串 1 0 # ((a))# 2 02 #( (a))# 3 022 #(( a))# 4 0223 #((a ))# 5 0224 #((A ))# 6 02245 #((A) )# 7 024 #(A )# 8 0245 #(A) # 9 01 #A # acc ∴此串为文法的句子. 例 2 G[E’]: (0) E’→E (1) E→E+n (2) E→n 其中 I1 中规约—移进冲突 ∴不是 LR(0)文法 例 3 G[A](0) A’→A (1)A→aAd (2)A→aAb (3) A→ε
A-add A→a4d 由项目()或LR(0)分析表均可看出:有冲突∴不是LR(0)文法 状态 a A 0 r3/s2 r3 r3 1 .acc r3/s2 r3 T3 3 b S4 S5 5 r2 r2 §6.3SLR(1)分析 P132LR(0)中有冲突则向前看一个对LR(0)分析表作局部政动如P134最上 例1如上例3 Fllow (A)=(#,b.da= ,·.是SLR1)文法 即遇到,b,d时规约,a时移进不规约,即把a列中的全部去掉 是LR(O),比是SLR(I) 、是SLR(1),未必是LRO) 步骏 状态栈 符号栈 输入串 0 2 a 3 022 #aa bd# 4 0223 #aaA 5 02235 #aaAb d# 6 023 7 0234 Ad 01 acc ∴#aabd#是文法的句子
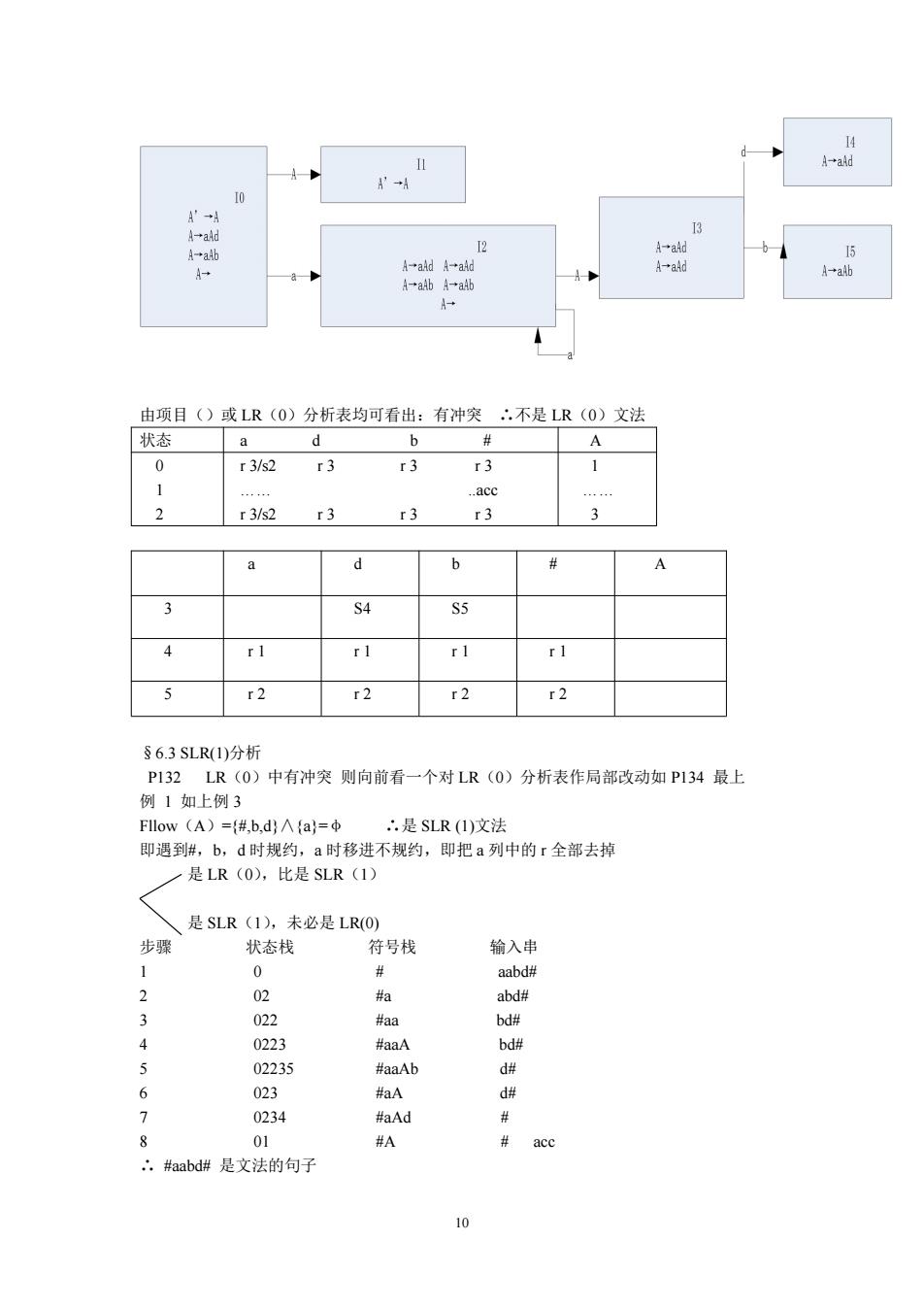
10 由项目()或 LR(0)分析表均可看出:有冲突 ∴不是 LR(0)文法 状态 a d b # A 0 1 2 r 3/s2 r 3 r 3 r 3 . .acc r 3/s2 r 3 r 3 r 3 1. 3 a d b # A 3 S4 S5 4 r 1 r 1 r 1 r 1 5 r 2 r 2 r 2 r 2 §6.3 SLR(1)分析 P132 LR(0)中有冲突 则向前看一个对 LR(0)分析表作局部改动如 P134 最上 例 1 如上例 3 Fllow(A)={#,b,d}∧{a}=φ ∴是 SLR (1)文法 即遇到#,b,d 时规约,a 时移进不规约,即把 a 列中的 r 全部去掉 是 LR(0),比是 SLR(1) 是 SLR(1),未必是 LR(0) 步骤 状态栈 符号栈 输入串 1 0 # aabd# 2 02 #a abd# 3 022 #aa bd# 4 0223 #aaA bd# 5 02235 #aaAb d# 6 023 #aA d# 7 0234 #aAd # 8 01 #A # acc ∴ #aabd# 是文法的句子