
第四章语法分析 4.14仍考虑练习4.6中的文法S→(L)川a L.3181S ()给出句子,(a,(》的一个最右推导,并指出右句型的句柄 ()按照(a)的最右 准导,说明移进一归约分析器的工作步骤,并给出它的分析树的自 下而上构造过程。 解:()S→L→LS→(L)→(LLS)→LLL)→L,(L,LS) →(L,L(L》→LL(Sa)→(L,(L(色a)→(L(⑤(aa) →L(山(aa》→L(Ls,(aa》→(L(L.a》→L,(,aa》 →(L,(但a助,(aa》→区(aa助,(aa》→(鱼(aa助,(aa》 (注:下划线部分为句柄) 6 步骤T 输入 动作 1 (a ((a a).(a.a)))5 25 a,(a,a),(a,a))s 移进 3 S(a ,(aa).(a.a))s 归约,S)a 4$S .a.a).(a.as 归约,L子S 55L .((a a).(a a5 移进 6 S(L. ((aa),(a.a))S 移进 7$L( (a.a).(aa)))s 移进 a.a).(a.a)))s 移讲 0 S(L ((a ,a).(aa) 归约,S)a 10 $(L.((S .a).(a.a))3 归约,L今S IsO CL a)(a al)s 移进 12$L(L a).(a.a)) 移讲 13 SL (L a ,(aa证 归约,S)a 14☐SL(LS ,(aa) 归约,LLS 15IsoL (L )(a.a))) 移进 16$L() (a.a)))s 归约.S)L) 17 S(L (S (a.a)))s 归约,L今S 18$L.L (aa)))s 移进 19S(L (L (aa))$ 移进 205L,L as 移进 5(L(L(a ,a))3 归的,S0 22 S(L,(L (S .a)3 归约,L今S 23 SL (L (L a)))s 移进 24 S(L.(L (L 移进 25 S(L (L (L a 归的,Sa 26 S(L (L (L.S 归约,LLS 27S(L (L (L DS 移诽
第四章 语法分析 4.14 仍考虑练习 4.6 中的文法 S → ( L ) | a L → L, S | S (a) 给出句子(a, ((a, a), (a, a)))的一个最右推导,并指出右句型的句柄; (b) 按照(a)的最右推导,说明移进-归约分析器的工作步骤,并给出它的分析树的自 下而上构造过程。 解:(a) S ➔ ( L ) ➔ (L, S) ➔ (L, (L)) ➔ (L, (L, S)) ➔ (L, (L, (L))) ➔ (L, (L, (L, S))) ➔ (L, (L, (L, a))) ➔ (L, (L, (S, a))) ➔ (L, (L, (a, a))) ➔ (L, (S, (a, a))) ➔ (L, ((L), (a, a))) ➔ (L, ((L, S), (a, a))) ➔ (L, ((L, a), (a, a))) ➔ (L, ((S, a), (a, a))) ➔ (L, ((a, a), (a, a))) ➔ (S, ((a, a), (a, a))) ➔ (a, ((a, a), (a, a))) (注:下划线部分为句柄) (b) 步骤 栈 输 入 动 作 1 $ (a, ((a, a), (a, a)))$ 移进 2 $( a, ((a, a), (a, a)))$ 移进 3 $(a , ((a, a), (a, a)))$ 归约,S→a 4 $(S , ((a, a), (a, a)))$ 归约,L→S 5 $(L , ((a, a), (a, a)))$ 移进 6 $(L, ((a, a), (a, a)))$ 移进 7 $(L, ( (a, a), (a, a)))$ 移进 8 $(L, (( a, a), (a, a)))$ 移进 9 $(L, ((a , a), (a, a)))$ 归约,S→a 10 $(L, ((S , a), (a, a)))$ 归约,L→S 11 $(L, ((L , a), (a, a)))$ 移进 12 $(L, ((L, a), (a, a)))$ 移进 13 $(L, ((L, a ), (a, a)))$ 归约,S→a 14 $(L, ((L, S ), (a, a)))$ 归约,L→L, S 15 $(L, ((L ), (a, a)))$ 移进 16 $(L, ((L) , (a, a)))$ 归约,S→(L) 17 $(L, (S , (a, a)))$ 归约,L→S 18 $(L, (L , (a, a)))$ 移进 19 $(L, (L, (a, a)))$ 移进 20 $(L, (L, ( a, a)))$ 移进 21 $(L, (L, (a , a)))$ 归约,S→a 22 $(L, (L, (S , a)))$ 归约,L→S 23 $(L, (L, (L , a)))$ 移进 24 $(L, (L, (L, a)))$ 移进 25 $(L, (L, (L, a )))$ 归约,S→a 26 $(L, (L, (L, S )))$ 归约,L→L, S 27 $(L, (L, (L )))$ 移进
28L.1.1) 29 $(L(LS 归约,LLS 30 S(L,(L 移进 31 SL (L) 归约,S)L) 3219 归约.L31 33 移进 34$L) 归约,S(四) 359 接受 分析树自上而下构造过程(略 4.15文法(428)的算符优先关系由表4.20给出,建立与表4.20相对应的算符优先函数并用算 符优先分析法分析句子(a,(a,a)。 解:如图所示 B. f. 可知:fa=2,ga=3,f(=8)=0,g(=3 f)=2f.=2:g.=1 f3=8$=0 对应的算符优先函数为: 0 0
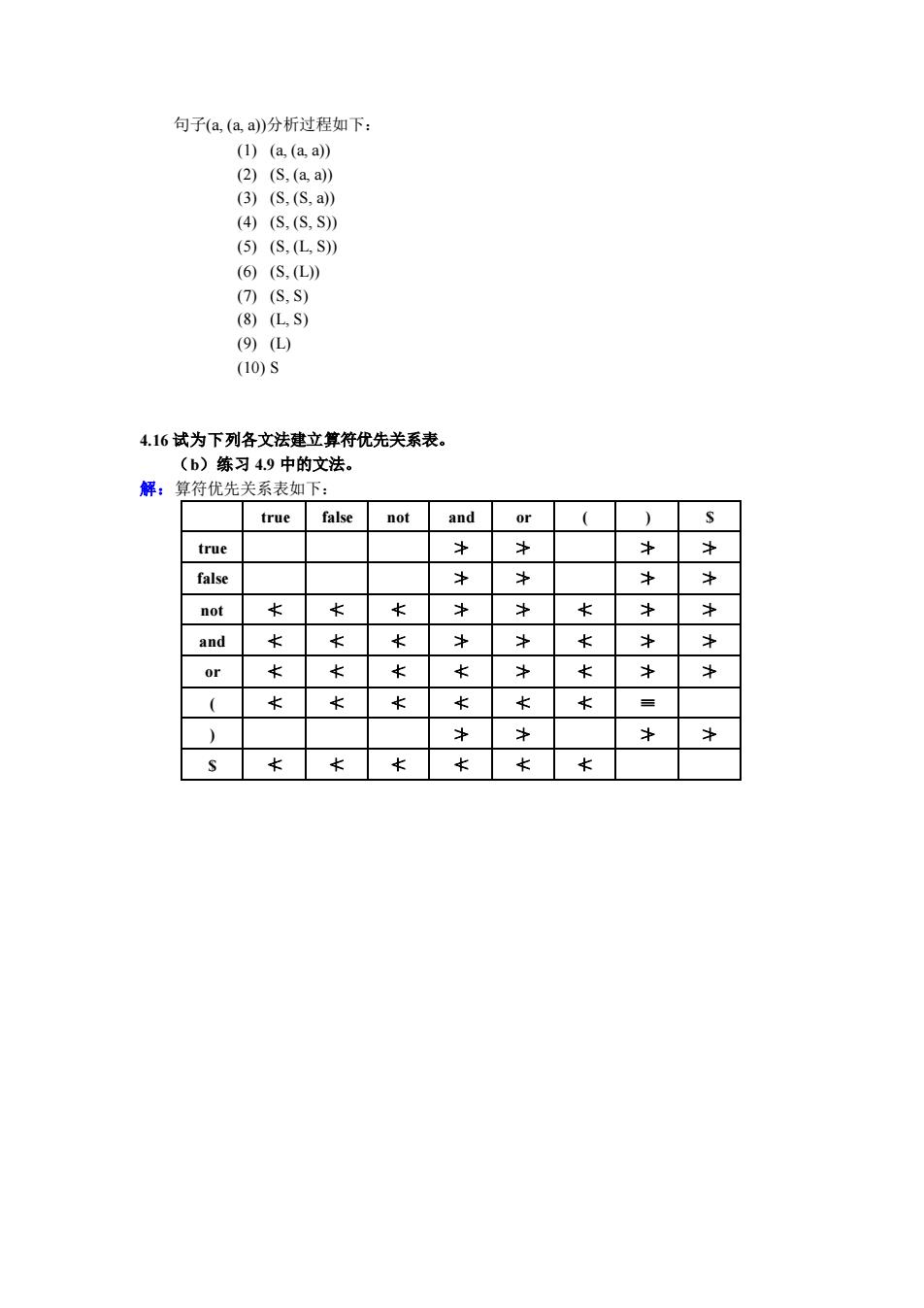
28 $(L, (L, (L) ))$ 归约,S→(L) 29 $(L, (L, S ))$ 归约,L→L, S 30 $(L, (L ))$ 移进 31 $(L, (L) )$ 归约,S→(L) 32 $(L, S )$ 归约,L→L, S 33 $(L )$ 移进 34 $(L) $ 归约,S→(L) 35 $S $ 接受 分析树自上而下构造过程(略) 4.15 文法(4.28)的算符优先关系由表 4.20 给出,建立与表 4.20 相对应的算符优先函数并用算 符优先分析法分析句子(a, (a, a))。 a ( ) , $ a ≯ ≯ ≯ ( ≮ ≮ ≡ ≮ ) ≯ ≯ ≯ , ≮ ≮ ≯ ≯ $ ≮ ≮ 解:如图所示: fa f) f, f$ g( g, g$ ga f(,g( 可知:f a = 2; g a = 3; f ( = g ) = 0; g ( = 3; f ) = 2; f , = 2; g , = 1; f $ = g $ = 0 对应的算符优先函数为: a ( ) , $ f 2 0 2 2 0 g 3 3 0 1 0
句子(a(aa)分析过程如下: ()(a(aa (2)(S,(aa 3)(S,(S,a) (4)(S,(S,S) (5)(S,LS) (6(S.(L) (5.s) (8)(LS) (9)(L) (10)s 4.16试为下列各文法建立算符优先关系表 (b)练习49中的文法。 解:算符优先关系表如下: true false e false not and
句子(a, (a, a))分析过程如下: (1) (a, (a, a)) (2) (S, (a, a)) (3) (S, (S, a)) (4) (S, (S, S)) (5) (S, (L, S)) (6) (S, (L)) (7) (S, S) (8) (L, S) (9) (L) (10) S 4.16 试为下列各文法建立算符优先关系表。 (b)练习 4.9 中的文法。 解:算符优先关系表如下: true false not and or ( ) $ true ≯ ≯ ≯ ≯ false ≯ ≯ ≯ ≯ not ≮ ≮ ≮ ≯ ≯ ≮ ≯ ≯ and ≮ ≮ ≮ ≯ ≯ ≮ ≯ ≯ or ≮ ≮ ≮ ≮ ≯ ≮ ≯ ≯ ( ≮ ≮ ≮ ≮ ≮ ≮ ≡ ) ≯ ≯ ≯ ≯ $ ≮ ≮ ≮ ≮ ≮ ≮
4.24下列文法是否为SLR(1文法?若是,请构造相应的分析表。若不是,请说明理由。 (a) S→SabbR RSa (b) S→aSAB|BA A2aAB Bh 解:(a)该文法的拓广文法G为: ()s→sab (2)s→bR (3)R→S (4)R→a 其LR(O)项目集规范族如下 10:S→S 13:S≥Sah 4:S→bR 5:R今S1 s→S·ab 1:s→s· 16:R>a S→S·ab 2:S→b.R 7:s→Sab, R→ R今·a sy·Sah SbR 文法G的识别活前缀的DFA如下所示: (3b(17 h (15 I2月 R(14 (16 FOLLOW(S)=FOLLOW=(a,$ 构造的SLR分析表如下: 状态 action goto R 0 92 93 S6 4 S7 观察左表,对状态5,可 归纳又可移进,即存在为重 r3/S3 定义的入口。 4 r4 所以,该文法不是 SLR文法
4.24 下列文法是否为 SLR(1)文法?若是,请构造相应的分析表。若不是,请说明理由。 (a) S ➔ S a b | b R R ➔ S | a (b) S ➔ a S A B | B A A ➔ a A | B B ➔ b 解:(a) 该文法的拓广文法 G’为: (0) S’→ S (1) S → Sab (2) S → bR (3) R → S (4) R → a 其 LR(0)项目集规范族如下: I0 : S’ → S· I3 : S → Sa·b S → ·Sab I4 : S → bR· S → ·bR I5 : R → S· S → S·ab I1 : S’ → S· I6 : R → a· S → S·ab I2 : S → b·R I7 : S → Sab· R → ·S R → ·a S → ·Sab S → ·bR 文法 G’的识别活前缀的 DFA 如下所示: S a b R a b a b S I0 I1 I2 I3 I5 I4 I7 I6 FOLLOW(S) = FOLLOW® = {a, $} 构造的 SLR 分析表如下: 观察左表,对状态 5,可 归纳又可移进,即存在为重 定义的入口。 所 以 , 该 文 法 不 是 SLR(1)文法。 状态 action goto a b $ S R 0 S2 1 1 S3 acc 2 S6 S2 5 4 3 S7 4 r2 r2 5 r3/S3 r3 6 r4 r4 7 r1 r1

(b)拓广文法G为: 0S→aSAB (2)S→BA (3)A→aA (4)A>B (⑤B→b 10:S° ·aSAB S→·BA B→·aB→·b :s*→s 2:B→b· B:S→a·SABS→·aSAB gS·RA By·b 4:SB·A A·B 5:s→ A→ ·aA A→·B B·b I6:S今aSA·B B→·b 7:A→a·A A→·B B→·b I8:S→BA· I9:S≥aSAB I10:A→aA 1:A今B 文法G'的识别活前缀的DFA如下图所示: 0s一 (I3 b I8 0 6 I2 又由FOLLOW(S)={ab,Sy FOLLOW(A)=(a,b,$ FOLLOW(B)=fa,b.$; 构造SLR分析表如下:
(b) 拓广文法 G’为: (0) S’ → S (1) S → aSAB (2) S → BA (3) A → aA (4) A → B (5) B → b 其 LR(0)项目集规范族如下: I0 : S’ → ·S S → ·aSAB S → ·BA B → ·a B → ·b I1 : S’ → S· I2 : B → b· I3 : S → a·SAB S →·aSAB S → ·BA B → ·b I4 : S → B·A A → ·aA A → ·B I5 : S → aS·AB A → ·aA A → ·B B → ·b I6 : S → aSA·B B → ·b I7 : A → a·A A → ·B B → ·b I8 : S → BA· I9 : S → aSAB· I10 : A → aA· I11 : A → B· 文法 G’的识别活前缀的 DFA 如下图所示: I0 I1 I3 I4 I2 I5 I8 I6 I7 I9 I10 I11 S S A B A A a B b B a b a B b b a b B 又由 FOLLOW(S) = {a, b, $} FOLLOW(A) = {a, b, $} FOLLOW(B) = {a, b, $} 构造 SLR 分析表如下:
状态 A S3 S2 S7 S2 显然,此分析表无多 S7 S2 重定义的入口。 2 所以,该文法为 1 rl 10 SLR)文法,其分析表 r3 左图所示 11r4 r4 r4 4.25证明下面文法是SLR(1)文法,并构造其SLR分析表 E→E+TIT T>TFIF F>F*lalb 解:其拓广文法G为: (0)E→E (1)E→E+T (2)E→T (3)T→T正 (4)T】 (5)F→F (6)F→a (7)Fb 其LRO)项目集规范族如下: I0:E≥·E E·E+T GS。T T→·F Fa F→·b 1:E→E E3E.+T 2:E→T T→T· F今·F* F→·a F→·b B:T→F· F)F·* 14:F3a. 15:F3b I6:E→E+·TT·T TF F·F Fa F→b 7:T→F· F子F·4 8·F3F* 9:E→E+·TT→TF F)F*F)a F→·b FOLLOW(E)=(+,$) FOLLOW(T)=(a b,+,$ FOLLOW(F)={ab,+,·,$} 其识别活前缀的DFA如图所示:
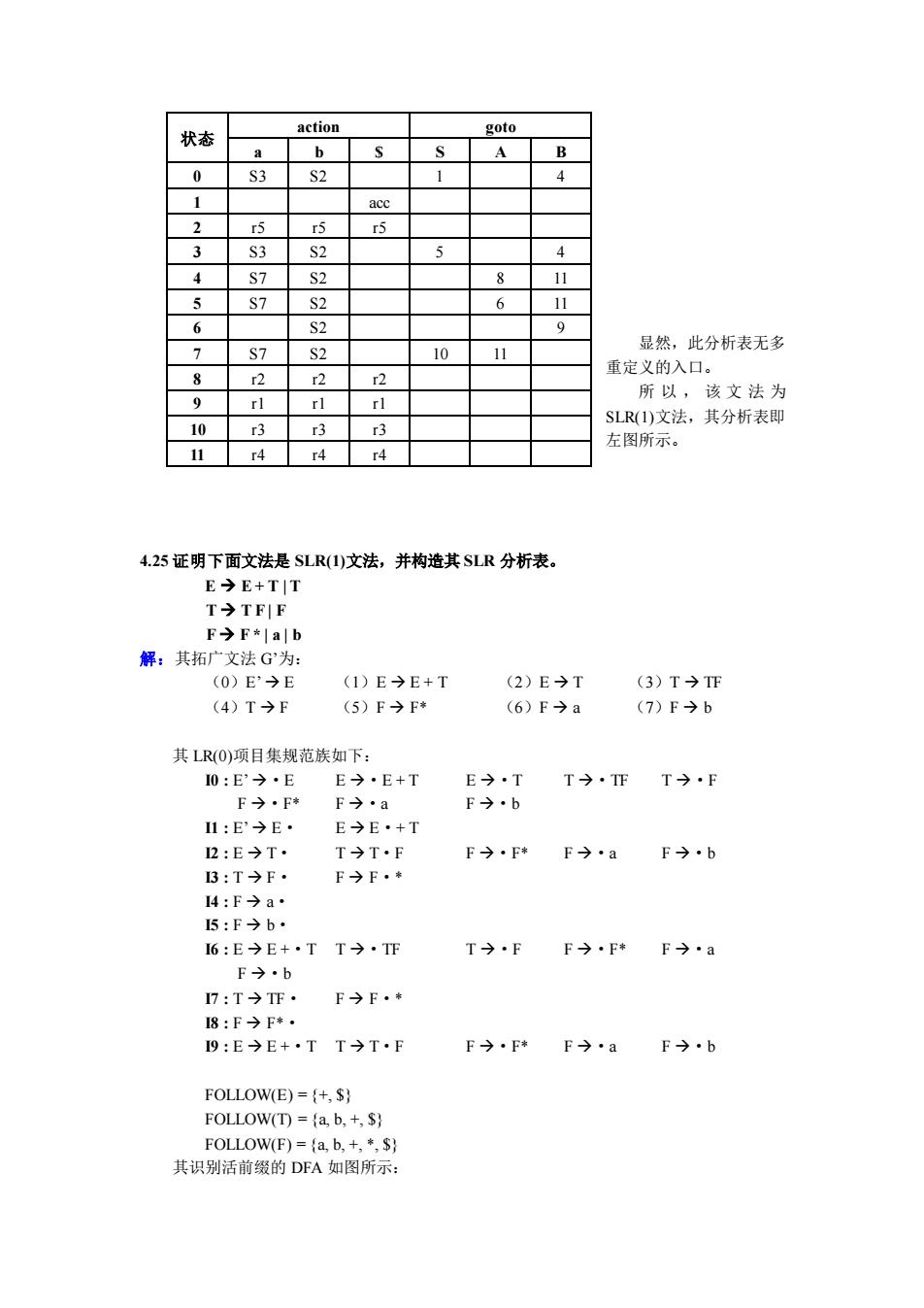
显然,此分析表无多 重定义的入口。 所 以 , 该 文 法 为 SLR(1)文法,其分析表即 左图所示。 4.25 证明下面文法是 SLR(1)文法,并构造其 SLR 分析表。 E → E + T | T T → T F | F F → F * | a | b 解:其拓广文法 G’为: (0)E’ → E (1)E → E + T (2)E → T (3)T → TF (4)T → F (5)F → F* (6)F → a (7)F → b 其 LR(0)项目集规范族如下: I0 : E’ →·E E →·E + T E →·T T →·TF T →·F F →·F* F →·a F →·b I1 : E’ → E· E → E·+ T I2 : E → T· T → T·F F →·F* F →·a F →·b I3 : T → F· F → F·* I4 : F → a· I5 : F → b· I6 : E → E +·T T →·TF T →·F F →·F* F →·a F →·b I7 : T → TF· F → F·* I8 : F → F*· I9 : E → E +·T T → T·F F →·F* F →·a F →·b FOLLOW(E) = {+, $} FOLLOW(T) = {a, b, +, $} FOLLOW(F) = {a, b, +, *, $} 其识别活前缀的 DFA 如图所示: 状态 action goto a b $ S A B 0 S3 S2 1 4 1 acc 2 r5 r5 r5 3 S3 S2 5 4 4 S7 S2 8 11 5 S7 S2 6 11 6 S2 9 7 S7 S2 10 11 8 r2 r2 r2 9 r1 r1 r1 10 r3 r3 r3 11 r4 r4 r4

E(11 I9 F 4 h 构造的SLR分析表如下: 状态 b F S4 S5 S6 r6 r6 7 7 r7 3 r3 8 r5r5 r5 15 9r1 9495r1 显然,此分析表无多重定义入口,所以此文法是SLR文法,其分析表如上图。 4.21考忠文法S→AS1b A→SA|a (a)构造文法的LR(O)项目集规范族及相应的DFA (b) 果把每 LR(O)项目看成 个状态, 并从每 一个形如B今a·XB的状态出发 画一条标记为X的箭弧刀状态B→aX·B,而且从每一个形如B今a·AB的 状态出发画标记为e的箭弧到所有形如A→·Y的状态。这样就得到了一个FA。 说明这个PA与(a)中的DFA是等价的。 (C)构造文法的SLR分析表。 (d)对于输入串bab,给出SLR分析器所作出的动作 (构造文法的LRI)分析表和LALR分析表 解:(a)令拓广文法G为 (0)s→S
I0 I1 I2 I3 I4 I5 I6 I7 I8 I9 E T F a b + F * T * a b F a b F a b 构造的 SLR 分析表如下: 状态 action goto + * a b $ E T F 0 S4 S5 1 2 3 1 S6 acc 2 S4 S5 7 3 r4 S8 r4 r4 r4 4 r6 r6 r6 r6 r6 5 r7 r7 r7 r7 r7 6 S4 S5 9 3 7 r3 S8 r3 r3 r3 8 r5 r5 r5 r5 r5 9 r1 S4 S5 r1 7 显然,此分析表无多重定义入口,所以此文法是 SLR 文法,其分析表如上图。 4.21 考虑文法 S → A S | b A → S A | a (a) 构造文法的 LR(0)项目集规范族及相应的 DFA。 (b) 如果把每一个 LR(0)项目看成一个状态,并从每一个形如 B → α·Xβ的状态出发 画一条标记为 X 的箭弧刀状态 B → αX·β,而且从每一个形如 B → α·Aβ的 状态出发画标记为ε的箭弧到所有形如 A → ·γ的状态。这样就得到了一个 NFA。 说明这个 NFA 与(a)中的 DFA 是等价的。 (c) 构造文法的 SLR 分析表。 (d) 对于输入串 bab,给出 SLR 分析器所作出的动作。 (e) 构造文法的 LR(1)分析表和 LALR 分析表。 解:(a) 令拓广文法 G’为 (0) S’ → S
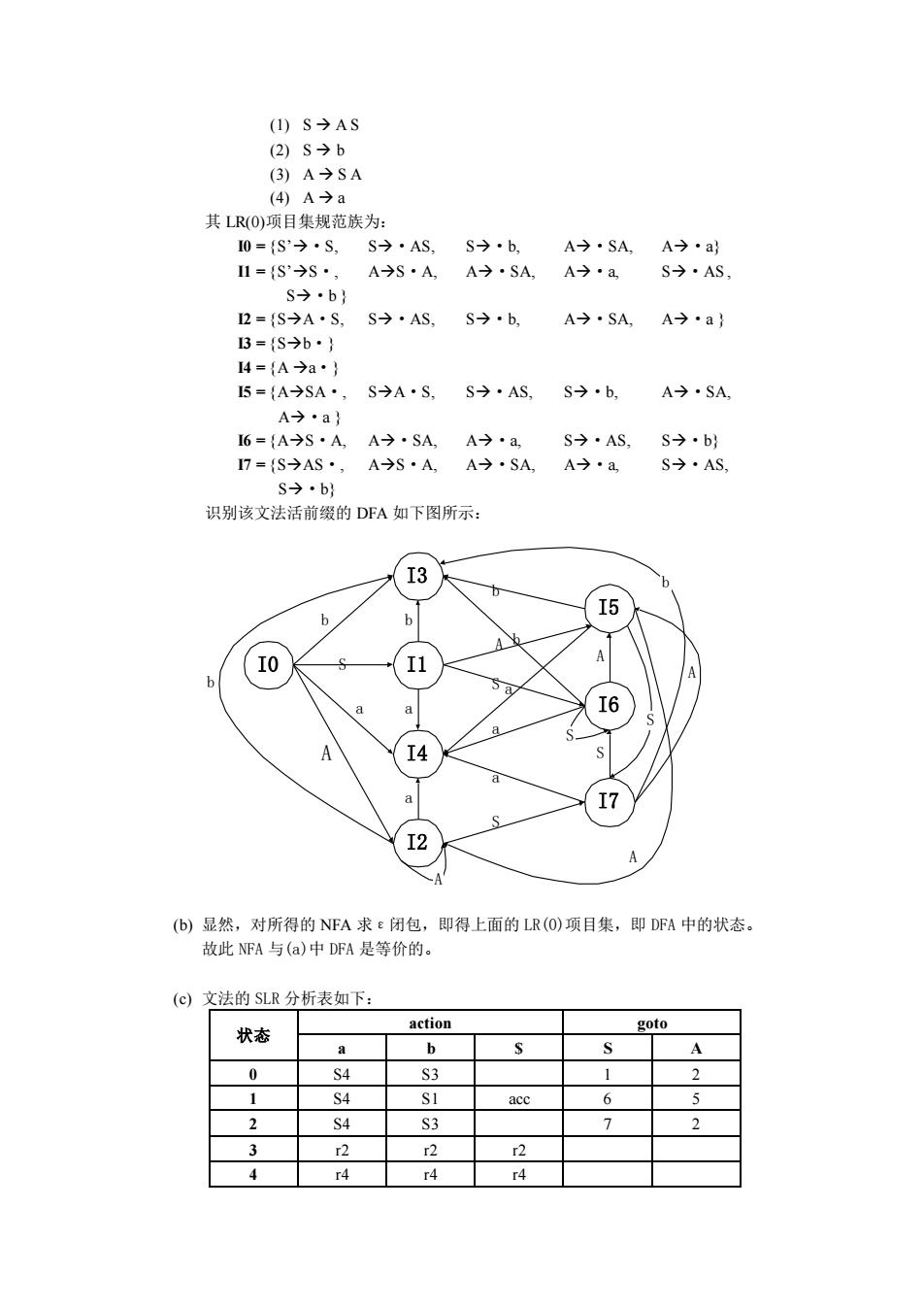
1)S→AS (2)s→b (3)A→SA (4)A今a 其LR(O)项目集规范族为: I0=4S→·S,S→·AS, g3。h A)·SA.A→·a} AS·A A→·SA A·a S·AS S→b 2=SA·S, S→·AS, s→b A→·SA,A→·a} 3=S→b· 14={A→a·} 5={A→SA· S→A·S, S→·AS, S→.b A→·SA a 6={A→S· A→·SA A→·a s→·AS, 7={S→AS·, A→S·A. A→·SA A→·a. S→·AS s→·by 识别该文法活前缀的DFA如下图所示: 3 6 b I5 h a a A I4 I2 (b)显然,对所得的NFA求E闭包,即得上面的LR(O)项目集,即DFA中的状态。 故此NFA与(a)中DFA是等价的 (c)文法的SLR分析表如下: action 状态 0 S4 1 S4 2 84 3 r2 4 r4 r4 r4
(1) S → A S (2) S → b (3) A → S A (4) A → a 其 LR(0)项目集规范族为: I0 = {S’→·S, S→·AS, S→·b, A→·SA, A→·a} I1 = {S’→S·, A→S·A, A→·SA, A→·a, S→·AS , S→·b } I2 = {S→A·S, S→·AS, S→·b, A→·SA, A→·a } I3 = {S→b·} I4 = {A →a·} I5 = {A→SA·, S→A·S, S→·AS, S→·b, A→·SA, A→·a } I6 = {A→S·A, A→·SA, A→·a, S→·AS, S→·b} I7 = {S→AS·, A→S·A, A→·SA, A→·a, S→·AS, S→·b} 识别该文法活前缀的 DFA 如下图所示: I0 I1 I3 I4 I2 I5 I6 I7 S a A b b a a b A b A A S b a a S S A A b S a S (b) 显然,对所得的 NFA 求ε闭包,即得上面的 LR(0)项目集,即 DFA 中的状态。 故此 NFA 与(a)中 DFA 是等价的。 (c) 文法的 SLR 分析表如下: 状态 action goto a b $ S A 0 S4 S3 1 2 1 S4 S1 acc 6 5 2 S4 S3 7 2 3 r2 r2 r2 4 r4 r4 r4

S4/r3S3/r3 r3 6 3 6 S4/rl S3/rl 6 (d对于输入串bab,SLR分析器所作出的动作如下: 栈 输入 动作 0 babs shift 0b3 abs reduce by S-→b 081 abs shift reduce by A→a 0S1A5 bs reduce by A→SA 0A2 h shift 0A2b3 reduce by b 0A2S7 shift by S→As 0S1 Accept (在第5个动作产生歧义) ()LR)项目集族为: I0:S→·S,s 1:S→s S→·AS,$lalb A→S·Aalb S→·b.$lalb A→·a.alb S→·SA,alb S·As alb A→·aalb s3.b,alb 2:s→A·S,$lalb l3:S今b·,$|alb s→·b,$lalb s→·As.$lalb I4:A→a·.alb A→SA.alb A→·aab 5:A→SA·,ab 6:A→S s→A·S,alb A→·SA.ab S→·AS,alb A→·a.alb Sy·b.alb S)·As.aIb A→·SAab S·b,alb A→·aab 7:S→AS·,alb A→S·Aalb A→·SA,ab Aaa1b S→·AS,ab S→·b,alb 6状态集中存在“归约一一移进”冲突,故无法构造L(1)分析表,因而也就无 法构造LALR分析表
5 S4 / r3 S3 / r3 r3 7 2 6 S4 S3 6 5 7 S4 / r1 S3 / r1 r1 6 5 (d) 对于输入串 bab,SLR 分析器所作出的动作如下: 栈 输入 动作 0 bab$ shift 0b3 ab$ reduce by S→b 0S1 ab$ shift 0S1a4 b$ reduce by A→a 0S1A5 b$ reduce by A→SA 0A2 b$ shift 0A2b3 $ reduce by S→b 0A2S7 $ shift by S→AS 0S1 $ Accept (在第 5 个动作产生歧义) (e) LR(1)项目集族为: I0 : S’ →·S, $ I1 : S’ → S· S →·AS, $ | a | b A → S·A, a | b S →·b, $ | a | b A →·a, a | b S →·SA, a | b S →·AS, a | b A →·a, a | b S →·b, a | b I2 : S →A·S, $ | a | b I3 : S → b·, $ | a | b S →·b, $ | a | b S →·AS, $ | a | b I4 : A → a·, a | b A →·SA, a | b A →·a, a | b I5 : A → SA·, a | b I6 : A → S· S → A·S, a | b A →·SA, a | b S → ·AS, a | b A →·a, a | b S →·b, a | b S →·AS, a | b A →·SA, a | b S →·b, a | b A →·a, a | b I7 : S → AS·, a | b A → S·A, a | b A →·SA, a | b A →·a, a | b S →·AS, a | b S →·b, a | b ∵I6 状态集中存在“归约――移进”冲突,故无法构造 LR(1)分析表,因而也就无 法构造 LALR 分析表