
推导A.B时.SELECT交集不为E,∴不能确定。“直接左递归A.有公共因子B 4.2LL(1)文法P74 4.3非LL(1)到LL(1)等价变换 1.提取左公共因子.p79 2.消除左递归 ,直接左递归的消除 ①EBNF:0表示重复0到若干次.{x小,即E,x,xx,·. 例G[E]:E一E+TT,T一T*FE,T一(E)|i EBNF:G[E]:E→T{+T,T→F{F}.F一(E)li 引入新非终结符。如改为右递归P82 la.B-Sblb G'[S]:S→h(a}或s-→b{a}等,A→Bcla,B-Sblb G[s]:S→AbS'bS'lcS,S'→aS|e,A→.,B-., 例2,G[s]:s→5 aPlSfIP,P-qbPlq,Q→c5dle G'[S]:S-P(aP}IP(f},P-. G[S]:S→Ps,s .一般左递归的消除 一,间接左递归的判断 ,头符号集:设有文法Gs=(Vn,L,P,S,则Vn上的头符号集HEAD(U)定义为: HEAD(U)=AU-+A.U,AEVn) 例:S-Uxy,U一Sz 则:S→Ux和S→Ux+Sx∴HEAD(S)=S,U U+Sz和U→Sz→Uz∴HEAD(U)=S,U仍 (事实上,HEAD(U是指从非终结符U出发能够推导出的所有符号串中,处于符号串头 得非终结符的集合) HEAD(U)的一般算法: 设文法G【S】不含E规则,并设初值HEAD(U=O,则。 ①考察文法的所有规则,若文法中有形如U一A的规则,则A∈HEAD(U): ②若P∈HEAD(U),则HEAD(P)∈HEAD(U) ③重复②,直到HEAD(U不再增大为止 ,显然,对文法GS]Vm,VLP,S)和任意非终结符U∈Vn,若U∈HEAD(U),则U为左递归 的非终结符,G【S】为左递归文法。(既可检测直接左递归和间接)
推导A.B时.SELECT交集不为ε,∴不能确定。∵直接左递归A.有公共因子B 4.2 LL(1)文法 P74 4.3 非LL(1)到LL(1)等价变换 1.提取左公共因子. p79 2.消除左递归 .直接左递归的消除 ①EBNF;{}表示重复0到若干次.{x},即ε,x,xx,. 例G[E];E→E+T|T,T→T*F|F,T→(E)|i EBNF;G`[E];E→T{+T},T→F{*F}.F→(E)|i 引入新非终结符。如 改为右递归P82 .例1 .G[S]:S→Sa|Ab|b|c. A→Bc|a,B→Sb|b G'[S]:S→Ab{a}或S→b{a}等,A→Bc|a,B→Sb|b G"[S]:S→AbS'|bS'|cS', S'→aS'|ε,A→.,B→., 例2, G[S]:S→SaP|Sf|P,P→QbP|Q,Q→cSd|e G'[S]:S→P{aP}|P{f},P→.,Q→., G"[S]:S→PS’,S’→aPS’|fS’|ε, P→.,Q→., .一般左递归的消除 一,间接左递归的判断 .头符号集:设有文法 G[s]=(Vn,Vt,P,S),则 Vn 上的头符号集 HEAD(U)定义为: HEAD(U)={A|U→+A. . .,U,A∈Vn} 例:S→Ux|y,U→Sz 则∵S→Ux 和 S→Ux→Szx,∴HEAD(S)={S,U} ∵U→Sz 和 U→Sz→Uxz ∴HEAD(U)={S,U} (事实上,HEAD(U)是指从非终结符 U 出发能够推导出的所有符号串中,处于符号串头 得非终结符的集合) HEAD(U)的一般算法: 设文法 G【S】不含ε规则,并设初值 HEAD(U)=∅,则。 ① 考察文法的所有规则,若文法中有形如 U→A.的规则,则 A∈HEAD(U); ② 若 P∈HEAD(U),则 HEAD(P) ∈ HEAD(U); ③ 重复②,直到 HEAD(U)不再增大为止 .显然,对文法 G[S]=(Vm,Vt,P,S)和任意非终结符 U∈Vn,若 U∈HEAD(U),则 U 为左递归 的非终结符,G【S】为左递归文法。(既可检测直接左递归和间接.)

例:GA]:A→BcdldD,B→ABb,C→c,D-AD]DBCa 首先令各非终结符的头符号集为空 ①根据GA]规则 得B∈HEAD(A A).A-HEAD(B).A,D.C HEAD(D .HEAD(A)=(B),HEAD(B)=A),HEAD(C)= HEAD(DFA,C,D ②,HEAD(A=B},所以HEAD(B)∈HEAD(A)所以HEAD(A)={AB: 同理HEAD(B)={A,B,HEAD(D){AB,C,D} ·AB,D为左递归的非终练 P83算法 该算法实际上是通过迭代,按排列顺序依次改变各非终结符的文法规则,使每个非终 结符的所有规则的右P只可能用其本身或排在其后的非终结符开头,从而使间接左递归直 接化,然后消除直接左递归,直至所有非终结符改造完毕为止 例:消除上述文法,即GA小: A-BcdldD.B-ABl]b.C-e.D-A D I DB]Ca GA的非终结符按 D排列 ②按算法=4,跟踪运行如下: 当i=l时,不能进入j循环,且规则A一→BcdldD不存在直接左递归,故文法不变 当=2时,=1时,改写规则B一AB: :A→BedldD所以B→AB改写为B→BedBldDB.∴B→BcdBldDBlb,. 消除关于B的直接左递归GA:A一→Bed]Dd,B→dDBB'lbB",B一cdBB'l C一D一 当=3,j=1或j=2时,由于关于C的规则,其右不以A,B开头,且C没有直接又递归,所以 文法不变。当I=4=1时,改为规则D一AD: 因为A一BdDd,所以D-AD改为D一BedDldDD所以D变为D-BedDldDD[DBICa =2时改写D+BcdD: 因为B一dDBB'lbB所以D-BedD改为D→dDBB'cdDbB'cdD所以D变为 =3时改为D→Ca 因为C→c所以DCa改为Dc 于是=4逃代完后D规则为: D-DBldDBB'cdDlbB'edDldDDlca A-BedldD. B-dDBB'lbB'B'-cdBB'l,C-cD-dDBB'cdDD'l bB'cdDD'dDDD'lcaD D'→BD'E 例P84G【sl:s→QccQ-RbbR→Saa 判断:1HEAD()F{Q,HEAD(QF{R;HEAD={S} 2.HEADXS)Q.R)HEADXQ) RS HEAD(R)-(S.Q 3.HEADX(S)=Q,RS HEAD(Q)={RS,QHEAD(R=S,Q,R是左递归 消除按SOR顺序排列 1j≠1S无直左文法不变」不等于1不进入循环 =2=1S不能带入O所以文法不变 i-3j-1 R一Sa,将S右P代入R,R一Qcalcal R-Qca, 将Q右P 代入R 消除直左:R一bcaR'lcaR'laR'R'→beaR'lE 按R,Q,S排列: i=l,j=0,R无直左,文法不变
例:G[A]:A→Bcd|dD,B→AB|b,C→c,D→AD|DB|Ca 首先令各非终结符的头符号集为空 ①根据 G[A]规则,得 B ∈ HEAD(A),A←HEAD(B).A,D,C HEAD(D) ∴HEAD(A)={B},HEAD(B)={A}, HEAD(C)=∅ HEAD(D)={A,C,D} ②∵HEAD(A)={B},所以 HEAD(B) ∈ HEAD(A) 所以 HEAD(A)={A,B} 同理 HEAD(B)={A,B}, HEAD(D)={A,B,C,D} ③重复②,∵个头符号集不在增大,∴G[A]有如上个头符号集 ∴ A,B,D 为左递归的非终结符,D 为直接左递归的非终结符,G[A]为左递归文法 一、消除一般左递归 P83 算法 该算法实际上是通过迭代,按排列顺序依次改变各非终结符的文法规则,使每个非终 结符的所有规则的右 P 只可能用其本身或排在其后的非终结符开头,从而使间接左递归直 接化,然后消除直接左递归,直至所有非终结符改造完毕为止 例:消除上述文法,即 G[A]:A→Bcd|dD,B→AB|b,C→c,D→AD|DB|Ca, ① G[A]的非终结符按 A,B,C,D 排列。 ② 按算法 n=4,跟踪运行如下: 当 i=1 时,不能进入 j 循环,且规则 A→Bcd|dD 不存在直接左递归,故文法不变 当 i=2 时,j=1 时,改写规则 B→AB: ∵A→Bcd|dD 所以 B→AB 改写为 B→BcdB|dDB. ∴B→BcdB|dDB|b, 消除关于 B 的直接左递归 G[A]:A→Bcd|Dd ,B→dDBB’|bB’,B’→cdBB’|ε C→.D→. 当 i=3 ,j=1 或 j=2 时,由于关于 C 的规则,其右不以 A,B 开头,且 C 没有直接又递归,所以 文法不变。当 I=4 j=1 时,改为规则 D→AD; 因为 A→Bcd|Dd, 所以 D→AD 改为 D→BcdD|dDD 所以 D 变为 D→BcdD|dDD|DB|Ca , j=2 时改写 D→BcdD; 因为 B→dDBB’|bB’ 所以 D→BcdD 改为 D→dDBB’cdD|bB’cdD 所以 D 变为. J=3 时 改为 D→Ca 因为 C→c 所以 D→Ca 改为 D→ca 于是 i=4 迭代完后 D 规则为:D→DB|dDBB’cdD|bB’cdD|dDD|ca A→Bcd|dD, B→dDBB’|bB’ B’→cdBB’|ε,C→c D→dDBB’cdDD’| bB’cdDD’| dDDD’ |caD’ D’→BD’|ε 例 P84 G【s】:S→Qc|c Q→Rb|b R→Sa|a 判断:1.HEAD(S)={Q},HEAD(Q)={R} HEAD={S} 2.HEAD(S)={Q,R} HEAD(Q)={R,S} HEAD(R)={S,Q} 3.HEAD(S)={Q,R,S} HEAD(Q)={R,S,Q} HEAD(R)={S,Q,R}∴是左递归 消除 按 S,Q,R 顺序排列 i=1 j≠1 S 无直左 文法不变 J 不等于 1 不进入循环 i=2 j=1 S 不能带入 Q 所以文法不变 i=3 j=1 R→Sa,将 S 右 P 代入 R,R→Qca|ca|a i=3 j=2 R→Qca,将 Q 右 P 代入 R R→Rbca|bca|ca|a 消除直左:R→bca R’|caR’|aR’ R’→bcaR’|ε 按 R,Q,S 排列: i=1,j=0,R 无直左,∴文法不变

i=2.j=1.Q-Rb,将R左p代入0,Q-Sablab/b =3j1,S→Qc,R无法代入S,不变 ,j2,s-一Qc,将Q代入S,S一 消直:S→abeS'IbeScS1,S一abcS1E.Q-.,R-.多余规则,删除 4.4不确定的自顶向下分析思想 P85 4.5确定的自顶向下分析方法 一递归子程序法(递归下降分析法)PASCAL.C米用 二山(1)法(预测分析法) 1.递归子程序法 根据文法写出语法分析程序 (1)对每一个非终结符U,编写一个相应子程序P(U) (2)对于规则U一x1Ix21.1Xm,可以构造P(U): if chIn FIRST(X1)THEN P(XI ELSE IFch IN ELSE IE FIRST(X2) THEN P(X2) ELSE ERROR (其中h为当前输入字符,是全程变量) (3)对于符号串xy1,y2ym,其相应子程序p(X)为: ②Y∈Vt.IFch -Yi THEN READ NEXT ERROR (当读的字符与符号匹配时,则读下一个。否则报错。) 特例:U一xllx2l.1Xale IF ch IN FOLLOW(U)THEN RETURN从A程序中出来到上一级 如前(3):ELSE IF ch-yi THEN ELSE ch∈Vn THEN. 例:GfS:s→aBC,B-bCldB],C-ch d1 SELECT(S-aBC)=a SELECT(B-→bC)={by SELECT(B-dB)=d SELECT(B-&)-FOLLOW(B)=FIRST(C)=(c.a) SELECTC-e)=fe) SELECT(C a=a ②相同左P的SELECT集两两相交,都为空∴.GS]是LL(1)文法
i=2,j=1,Q=Rb,将 R 左 P 代入 Q,Q→Sab|ab|b i=3,j=1,S→Qc,R 无法代入 S,∴不变 i=3,j=2,S→Qc,将 Q 代入 S,S→Sabc|abc|bc|c 消直:S→abcS’|bcS’|cS’|,S’→abcS’|ε.Q→.,R→. 多余规则,删除 4.4 不确定的自顶向下分析思想 P85 4.5 确定的自顶向下分析方法 一 递归子程序法(递归下降分析法)PASCAL.c 来用 二 LL(1)法(预测分析法) 1.递归子程序法 根据文法写出语法分析程序: (1) 对每一个非终结符 U,编写一个相应子程序 P(U) (2) 对于规则 U→x1|x2|.|Xn,可以构造 P(U); IF ch IN FIRST(X1) THEN P( X1) ELSE IF ch IN FIRST(X2) THEN P(X2) ELSE IF . . ELSE ERROR (其中 ch 为当前输入字符,是全程变量) (3) 对于符号串 x=y1,y2.ym,其相应子程序 P(X)为: ① Yi∈Vn,程序就调用 Yi 相对应子程序:P(y1);P (y2);. ② Yi∈Vt,IF ch=Yi THEN READ NEXT ch ELSE ERROR (当读的字符与符号匹配时,则读下一个。否则报错。) 特例:U→x1|x2|.|Xn|ε IF ch IN FOLLOW(U) THEN RETURN 从 A 程序中出来到上一级 如前(3):ELSE IF ch=yi THEN. ELSE ch∈Vn THEN . . . . . . . 例:G[S]:S→aBC,B→bC|dB|ε,C→c|a ① SELECT(S→aBC)={a} SELECT(B→bC)={b} SELECT(B→dB)={d} SELECT(B→ε)=FOLLOW(B)=FIRST(C)={c,a} SELECT(C→c)={c} SELECT(C→a)={a} ② 相同左 P 的 SELECT 集两两相交,都为空 ∴G[S]是 LL(1)文法
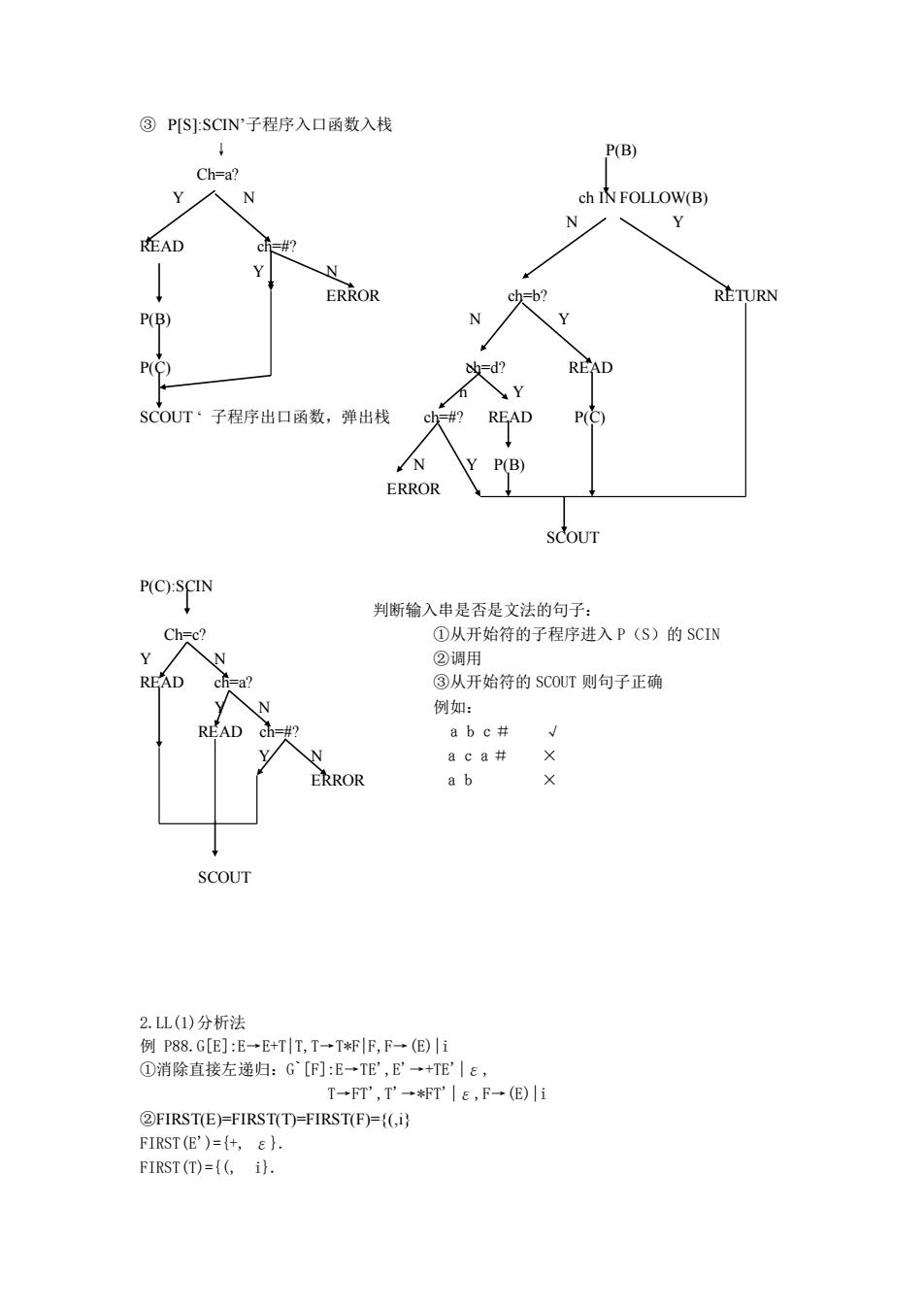
③PS:SCN子程序入口函数入栈 P(B) Ch=a? ch IN FOLLOW(B) N Y READ N ERROR b P(B) N P(C) =d2 SCOUT·子程序出口函数,弹出栈 N ERROR P(C):SCIN 判断输入串是否是文法的句子: Ch=c? ①从开始符的子程序进入P(S)的SCIW ②调用 ③从开始符的SC0UT则句子正确 例如: AD a b c# √ N a c a X ERROR ab SCOUT 2.L(1)分析法 例P88.G[E]:E→E+TlT,T→TFE,F→(E)|i O消除直接左递归:G[F]:E→TE',E一+TE|e TFT',T→T|e,F一(E)i @FIRST(E)=FIRST(T)=FIRST(F)=.i) FIRST(E')=(+,) FIRST(T)={(,i)
③ P[S]:SCIN’子程序入口函数入栈 ↓ P(B) Ch=a? Y N ch IN FOLLOW(B) N Y READ ch=#? Y N ERROR ch=b? RETURN P(B) N Y P(C) ch=d? READ n Y SCOUT ‘ 子程序出口函数,弹出栈 ch=#? READ P(C) N Y P(B) ERROR SCOUT P(C):SCIN 判断输入串是否是文法的句子: Ch=c? ①从开始符的子程序进入 P(S)的 SCIN Y N ②调用 READ ch=a? ③从开始符的 SCOUT 则句子正确 Y N 例如: READ ch=#? abc# √ Y N aca# × ERROR ab × SCOUT 2.LL(1)分析法 例 P88.G[E]:E→E+T|T,T→T*F|F,F→(E)|i ①消除直接左递归:G`[F]:E→TE',E'→+TE'|ε, T→FT',T'→*FT'|ε,F→(E)|i ②FIRST(E)=FIRST(T)=FIRST(F)={(,i} FIRST(E')={+, ε}. FIRST(T)={(, i}

FIRST(T)={*,E上. FIRST(F)=((,i). F0L0m(@)=U()J=(#,) FOLLOW (E')=FOLLOW (E)={#) FOLLOW(T)=FIRST(E')\E UFOLLOW (E)UFOLLOW (E')=(+#) FOLLOW (T')=FOLLOW(T)=#) FOLLOW (F)=FIRST(T')\E UFOLLOW (T)UFOLLOW (T")=(*,+,#)} SELECT(E-TE')=FIRST(T)=FIRST(T)=((i SFLCT(E'→+TE')=(+ SELECT(E'→e)=FOLL0R(E')={供,)J SELECT(T-FT')=FIRST(F)=((,i) SELECT(T'→*FT')={*} SELECT(T一e)=FOLLOW(T)=+,#,)) SELECT(F-→(@)={O SELECT(F→i)={i) ③看同一左P的SELECT集,是否有空集,此题无,故为L(1)文法 ④画出分析表 LL(1)分析表: TE →TE E' +TE' e →FT -FT/ T -8 *FT 8 ·(E) ⑤右表中是否有重叠,此题无 ⑥总控工作过程:总控程序是根据分析栈的栈顶符号x,当前输入符号a,决定下一个动作 算法:(1)分析栈顶放一个“#”,再放文法开始符,反复执行步骤(2) (2)设定分析的某一步,对于任何(x,a),总控程序执行下述三种可能之一。 A.如果x=a=”#“,则宜布分子成功,停止分析过程 b.如果x=a≠"#”,则将x出栈,i让a指向下一个输入符号 C.如果x∈m,查看分析表M,若M[x,a】中存放关于x的一个产生式,首先将x出 栈,再将产生式的右P符号申按逆序一一推进栈,(若右P符号为?,则不进栈),若M[x,] 中存放着“出错标志”,则报错
FIRST(T')={*, ε}. FIRST(F)={(, i}. FOLLOW(E)={#}∪{)}={#, )} FOLLOW(E')=FOLLOW(E)={#, )} FOLLOW(T)=FIRST(E')\ ε∪FOLLOW(E)∪FOLLOW(E')={+, #, )} FOLLOW(T')=FOLLOW(T)={+, #, ) } FOLLOW(F)=FIRST(T')\ ε∪FOLLOW(T)∪FOLLOW(T’)={*,+,#,)} SELECT(E→TE')=FIRST(T')=FIRST(T)={(, i } SELECT(E'→+TE')={+} SELECT(E'→ε)=FOLLOW(E')={#, ) } SELECT(T→FT')=FIRST(F)={(, i} SELECT(T'→*FT')={*} SELECT(T'→ε)=FOLLOW(T')={+, #, ) } SELECT(F→(E))={(} SELECT(F→i)={i} ③看同一左P的SELECT集,是否有空集,此题无,故为LL(1)文法 ④画出分析表 LL(1)分析表: + * ( ) i # E →TE' →TE' E' →+TE' →ε →ε T →FT' →FT' T' →ε →*FT' →ε →ε F →(E) →i ⑤看表中是否有重叠,此题无 ⑥总控工作过程:总控程序是根据分析栈的栈顶符号X,当前输入符号a,决定下一个动作 算法:(1)分析栈顶放一个“#”,再放文法开始符,反复执行步骤(2) (2)设定分析的某一步,对于任何(x,a),总控程序执行下述三种可能之一: a.如果x=a="#",则宣布分子成功,停止分析过程 b.如果x=a≠"#”,则将x出栈,让a指向下一个输入符号 c.如果 x∈Vn,查看分析表 M,若 M[x,a]中存放关于 x 的一个产生式,首先将 x 出 栈,再将产生式的右 P 符号串按逆序一一推进栈,(若右 P 符号为?,则不进栈),若 M[x,a] 中存放着“出错标志”,则报错

步骤 分析栈 输入串 i计i*i# 23 4 HE'Ti i+i*i #E'T' +i*i# 6 +i*i# 89 #E'T万 #E'T'i #E'T * #E'T'F* 4 16 #E'T #E 11 ·i+i*i进是该文法的句子 例:G[S]:S一aBc|bAB,A一abb,B-blE ①SELECT(S→aBc)=Ial SELECT(S-→bAB)=fbl SELECT(A→aAb)=(a SELECT(A→b)={6 SELECT(B-b)={b} SELECT (B-E)=FOLLOW(B)=c}UFOLLOW(S)=(c,# 此文法为L(1)文法,画出LL()分析表 ② a b →aBg →bAB -aA b b
步骤 分析栈 输入串 1 #E i+i*i# 2 #E'T i+i*i# 3 #E'T'F i+i*i# 4 #E'T'i i+i*i# 5 #E'T' +i*i# 6 #E' +i*i# 7 #E'T+ +i*i# 8 #E'T i*i# 9 #E'T'F i*i# 10 #E'T'i i*i# 11 #E'T' *i# 12 #E'T'F* *i# 13 #E'T'F i# 14 #E'T'i i# 15 #E'T' # 16 #E' # 17 # # ∴ i+i*i# 是该文法的句子 例:G[S]:S→aBc|bAB, A→aAb|b, B→b|ε ①SELECT(S→aBc)={a} SELECT(S→bAB)={b} SELECT(A→aAb)={a} SELECT(A→b)={b} SELECT(B→b)={b} SELECT(B→ε)=FOLLOW(B)={c}∪FOLLOW(S)={c,#} ∴此文法为LL(1)文法,画出LL(1)分析表 ② a b c # S →aBc →bAB A →aAb →b B →b →ε →ε

③判断baabbb是否为句子 步 分析栈 输入串 #5 baabbb# 2 #BAb baabbb# 2 #BA aabbb 45 aabbb #BbA abbb# 6 BbbAa abbb 7 BbbA bbb¥ 8 #Bbbh bbb (LL(1)文法的实质是最左推导例 #B 带入上式) 12 “该符号串是文法的句子 第五章自底向上优先分析法 例:G[S]:S→aAcBe,.A一b,A一Ab,B一d.看申abbede 推导:S→aAcBe-→ aA b c B e a bb c B e-a bb c d e 归约 对树进行剪枝动作,把句柄进行归约 ①A+b②B +d③A←Ab④S←a A c B e aA c 如为规范归约,找句柄,是唯一规约的一一一LR(k) 自底向上分析法 算符归约是非规范归约,找可归约串最左语一一算符优先一 找优先关系,如上例:abbcde,如找到a.则b优先级最高 先归约b,aAb cd e,只归约终结符,ac,.则b优先级高, 根据性质b带附远非终结符,即ac,规约为a A c B e, 再找到##,再把前后非终结符带上归约
③判断baabbb#是否为句子 步骤 分析栈 输入串 1 #S baabbb# 2 #BAb baabbb# 3 #BA aabbb# 4 #BbAa aabbb# 5 #BbA abbb# 6 #BbbAa abbb# 7 #BbbA bbb# 8 #Bbbb bbb# (LL(1)文法的实质是最左推导例 9 #Bbb bb# 推导;S aAcBeAaBC逆序进 10 #Bb b# 栈,A在栈顶,用A→abc的右P代替左P, 11 #B # 带入上式) 12 # # ∴该符号串是文法的句子 第五章 自底向上优先分析法 例:G[S]:S→aAcBe,A→b,A→Ab,B→d.看串abbcde 推导:S→ aAcBe→ aAbcBe→ abbcBe→ abbcde 归约 S 对树进行剪枝动作,把句柄进行归约 ①A←b ②B ←d③A←Ab ④S← aAcBe a A c B e A b d b 如为规范归约,找句柄,是唯一规约的———LR(k) 自底向上分析法 算符归约是非规范归约,找可归约串最左 语——算符优先 找优先关系,如上例:abbcde,如找到a<.b.>...则b优先级最高。 先归约b,aAbcde,只归约终结符,a<.b.>c,...则b优先级高, 根据性质b带附远非终结符,即a<.Ab.>c...规约为aAcBe, 再找到#<.a=c=e.>#,再把前后非终结符带上归约

规范归约DC,BD,A←B,C一ACD四步归约 非规范归约D一c,C←ccD,(只看终结符) 两步归约 ,如aBb,aa,b与a的优先关系不能确定 P100 二,算法代先,定义,性质 PI02二,FIRSTUT集LASTUT集定义 1、FIRSTUT(A)的算法: (1)若有产生式A+b.,或A→Bb.,则b∈FRST几UTA) (2)若有b∈FIRSTUT(B).且有产生式A→B,则b∈FIRSTUT(A) 2、LASTUT(A)的算法: 若有产生式A一.a或A- aB,则a∈LASTUT(A) (2)若有a∈LASTUT(B),且有产生式A一B,则a∈LASTUT(A) P102例1.E-E+TITTTFFF-P+IPP→(E 求每个非终结符的FIRSRUT和LASTUT集 FIRSTUT(E)=(+UFIRSTUT(T)=+,*,↑,(i) FIRSTUT(T)={JFIRSTUT(F)=(w,↑,(,i) FIRSTUT(F)=(↑)UFIRSTUT(P)=(↑,(,i) FIRSTUT(P)=((.i) LASTUT(E)={+)ULASTUT(T)=*,+,↑,),iJ LASTUT(T)=*}ULASTUT(F)={*,↑,),i} LASTUT(F)={↑}ULASTUT(P)={↑,),iJ LASTUT (P)=0.i) 例2.G[S]:S-→S:DDD-D(T)I日H→a(S)T→T+sls FIRSTUT(S)=(:}UFIRSTUT(D)=(:.a.c} FIRSTUT(D)=((}UFIRSTUT(H)=(a,c} FIRSTUT(H)=a c) FIRSTUT(T)=(+)UFIRSTUT(S)=(+.:.a.c} LASTUT(S)=(:)ULASTUT(D):.)} LASTUT(D)=0)ULASTUT(H)=a.) LASTUT (H)=(a.) LASTUT(T)=(+)ULASTUT(S)=+,:.a.) 三,构造文法算符优先矩阵 一般算法 ①对文法G[s】的每一非终结符构造FIRSTUT和LASTUT集 ②如书P102.a),b),c)
规范归约 D←C,B←D,A←B,C←ACD 四步归约 非规范归约D←c,C←ccD,(只看终结符) 两步归约 .如aBb,aa,b 与 a 的优先关系不能确定 P100 一,算法优先,定义,性质 P102 二,FIRSTUT 集 LASTUT 集定义 1、 FIRSTUT(A)的算法: (1) 若有产生式 A→b.或 A→Bb.,则 b∈FIRSTUT(A) (2) 若有 b∈FIRSTUT(B),且有产生式 A→B,则 b∈FIRSTUT(A) 2、 LASTUT(A)的算法: (1) 若有产生式 A→.a 或 A→.aB,则 a∈LASTUT(A) (2) 若有 a∈LASTUT(B),且有产生式 A→B, 则 a∈LASTUT(A) P102 例1.E→E+T|T T→T*F|F F→P↑+F|P P→(E)|i 求每个非终结符的FIRSRUT和LASTUT集 FIRSTUT(E)={+}∪FIRSTUT(T)={+,*,↑,(,i} FIRSTUT(T)={*}∪FIRSTUT(F)={*,↑,(,i} FIRSTUT(F)={↑}∪FIRSTUT(P)={↑,(,i} FIRSTUT(P)={(,i} LASTUT(E)={+}∪LASTUT(T)={*,+,↑,),i} LASTUT(T)={*}∪LASTUT(F)={*,↑,),i} LASTUT(F)={↑}∪LASTUT(P)={↑,),i} LASTUT(P)={),i} 例2.G[S]:S→S;D|D D→D(T)|H H→a|(S) T→T+S|S FIRSTUT(S)={;}∪FIRSTUT(D)={;,a,c} FIRSTUT(D)={(}∪FIRSTUT(H)={a,c} FIRSTUT(H)={a,c} FIRSTUT(T)={+}∪FIRSTUT(S)={+,;,a,c} LASTUT(S)={;}∪LASTUT(D)={;,a,)} LASTUT(D)={)}∪LASTUT(H)={a,)} LASTUT(H)={a,)} LASTUT(T)={+}∪LASTUT(S)={+,;,a,)} 三,构造文法算符优先矩阵的一般算法: ①对文法G[s]的每一非终结符构造FIRSTUT和LASTUT集。 ②如书P102.a),b),c)