
上泽充通大学 LECTURE 12 Gears-Design for Strength 齿轮强度设计 Covered Cha5 and Cha6 In Mechanical Engineering Design 上游文大学 outline SCHAI IAO TONG UNIVEROITY 1.Forces on Gears 2.Failure types of gears 3.Material selection of gear 4.Fundamental theories for gearing strength
1 Gears-Design for Strength 齿轮强度设计 LECTURE 12 Covered Cha5 and Cha6 In Mechanical Engineering Design outline 1.Forces on Gears 2.Failure types of gears 3.Material selection of gear 4.Fundamental theories for gearing strength

上海文通大学 Forces on gears Forces on spur gears Forces on helical gears Forces on bevel gears Forces on worm gears Refer to Chapter 5 in Mechanical engineering design 上游文大学 ANGHAI HAO TONG UNIVEROIT H W,=33000- +3+3→ where W.transmitted load,Ibf H=power,hp V=pitch-line velocity,ft/min 60000H W,= ndn where W,=transmitted load,kN H=power,kW d=gear diameter,mm n=speed,rev/min 3*15
2 Refer to Chapter 5 in Mechanical engineering design Forces on spur gears Forces on helical gears Forces on bevel gears Forces on worm gears Forces on gears
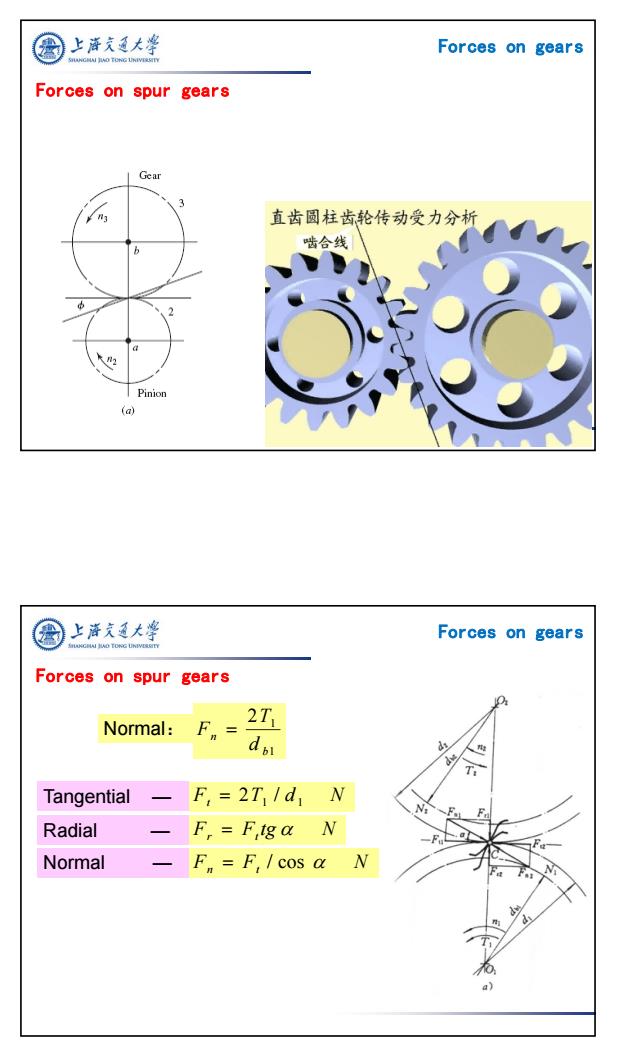
上泽充通大学 Forces on gears Forces on spur gears Gear 直齿圆柱齿轮传动受力分析 啮合线 Pinion (a) 上游久通大学 Forces on gears ANGHAI HAO TONG UNIVEROIT Forces on spur gears Normal: 2T Tangential F,=2T/d1 N Radial F.=Ftga N Normal F=F/cos a N a)
3 Forces on gears Forces on spur gears Normal: Tangential — 1 1 2 b n d T F Ft 2T1 / d1 N Radial — Fr Ft tg N Normal — Fn Ft / cos N Forces on gears Forces on spur gears
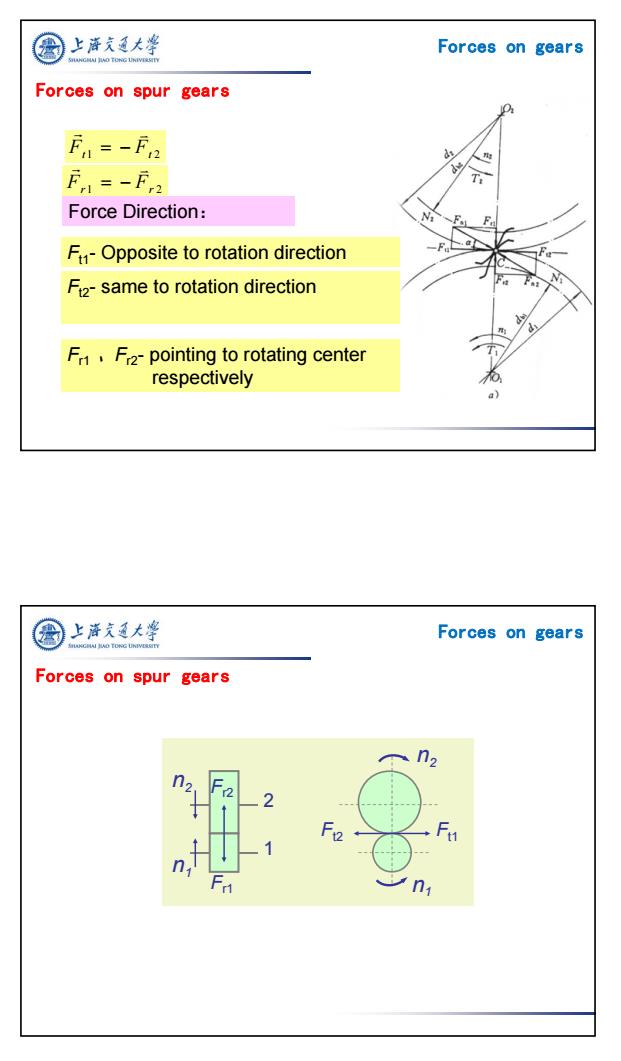
上浒充通大学 Forces on gears Forces on spur gears E=-F2 F=-F2 Force Direction: F-Opposite to rotation direction F2-same to rotation direction F,F2-pointing to rotating center respectively 上濟大学 Forces on gears ANGHAI HAO TONG UNIVEROIT Forces on spur gears n2
4 Ft1 Ft 2 Fr 1 Fr 2 Force Direction: Ft1- Opposite to rotation direction Ft2- same to rotation direction Fr1 、Fr2- pointing to rotating center respectively Forces on gears Forces on spur gears 2 1 n2 n1 Fr2 Fr1 Ft2 Ft1 n1 n2 Forces on gears Forces on spur gears
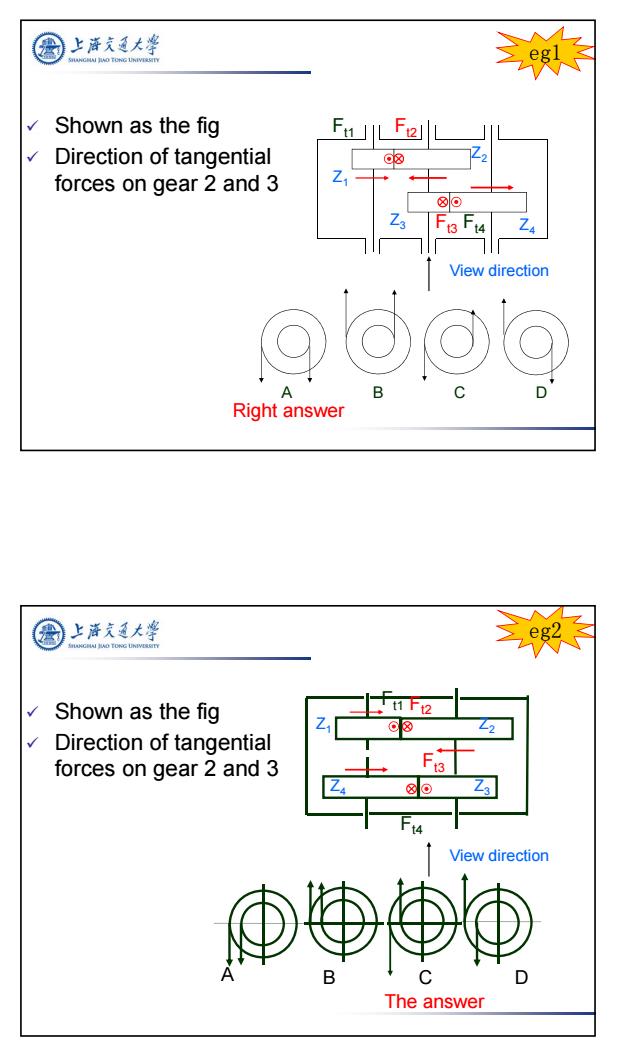
上泽充通大学 Shown as the fig Direction of tangential 8 forces on gear 2 and 3 ⑧o View direction ©⊙@o B Right answer 上游文大学 UGHAI HAO TONG UNIVEROI Shown as the fig 十t1F2 @⑧ Direction of tangential forces on gear 2 and 3 ⑧ Z3 View direction The answer
5 Shown as the fig Direction of tangential forces on gear 2 and 3 Right answer eg1 View direction Z1 Z4 Z2 Z3 A BCD Ft1 Ft2 Ft3 Ft4 The answer eg2 Z4 Z3 Z1 Z2 Ft2 Ft1 Ft4 Ft3 A BCD Shown as the fig Direction of tangential forces on gear 2 and 3 View direction
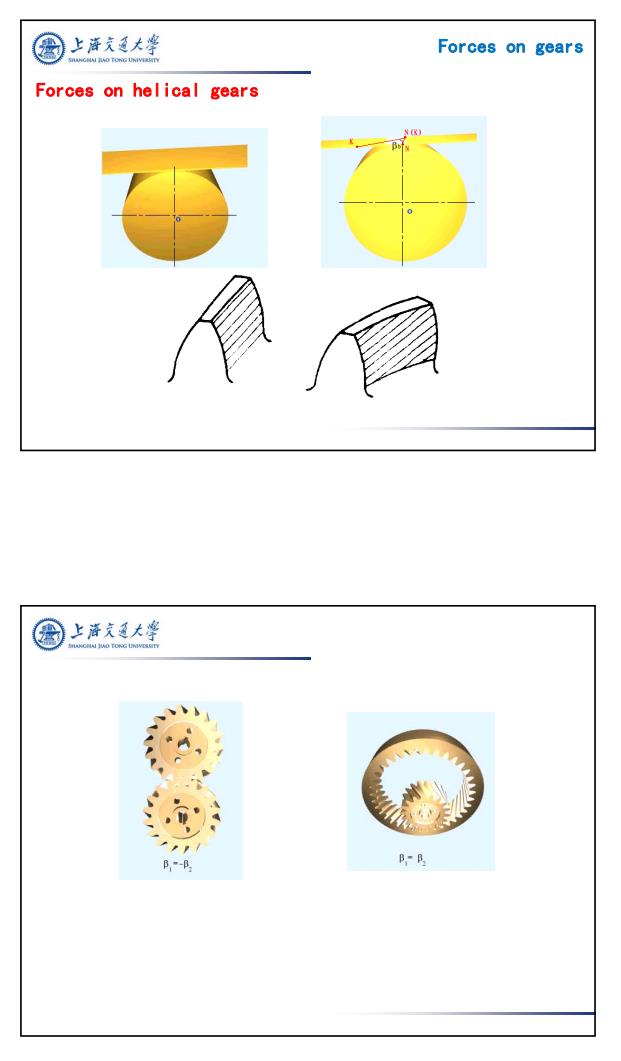
上游充廷大¥ Forces on gears Forces on helical gears 上游文大学 FANGHAI HO TONG UNIVERSITY B--B. B-E
6 Forces on gears Forces on helical gears
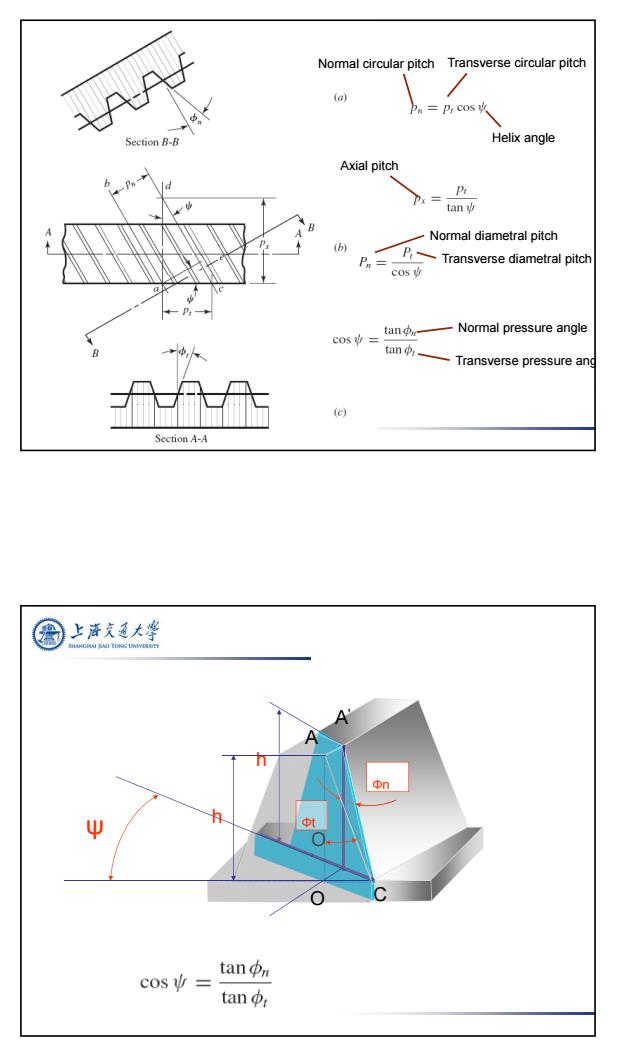
Normal circular pitch Transverse circular pitch (a) =P,Cos攻 Section B-B Helix angle Axial pitch P Px= tan Normal diametral pitch (b) P= PTransverse diametral pitch cos cos女= tan中m Normal pressure angle tan -Transverse pressure ang (e) SectionA-A 上游文大学 FANGHAI HO TONG UNIVERSITY Φn cos= tan n tan
7 Normal circular pitch Transverse circular pitch Helix angle Axial pitch Normal diametral pitch Transverse diametral pitch Normal pressure angle Transverse pressure ang Φn h A' C O ' h Φt O A ψ

上海久通大¥ NO Nomenclatures formulus 1 摄置装装eodu m.is standardized m 2 型e B=820° 3 ransverse presourg,angle 端面压力角 =aretga.is standardized 4 pitch Diameterd、d 分度圆直径 4=m=m, cosB d=m2=m点 Addendum 齿顶高 b。 五。=研、 6 Dedendum hr b,=1.25m, 背我 k=在,十A,=2.25m, 8 蜀e e Gah,-h。=0.25m。 ddendum diamate、da 齿顶圆直经 d1d1+24,d.:sd:+2h。 9 edendum diamete,、da 齿根图直径 d:=d1-2克,d,2=d-2, 2 Central distance a a=d十生=n白,+)=m3+) 中心距 2 2 cosp 上游久通大学 Forces on gears ANGHAI HAO TONG UNIVEROIT Forces on helical gears 斜齿圆柱齿轮传动受力分析 12 0
8 Forces on gears Forces on helical gears
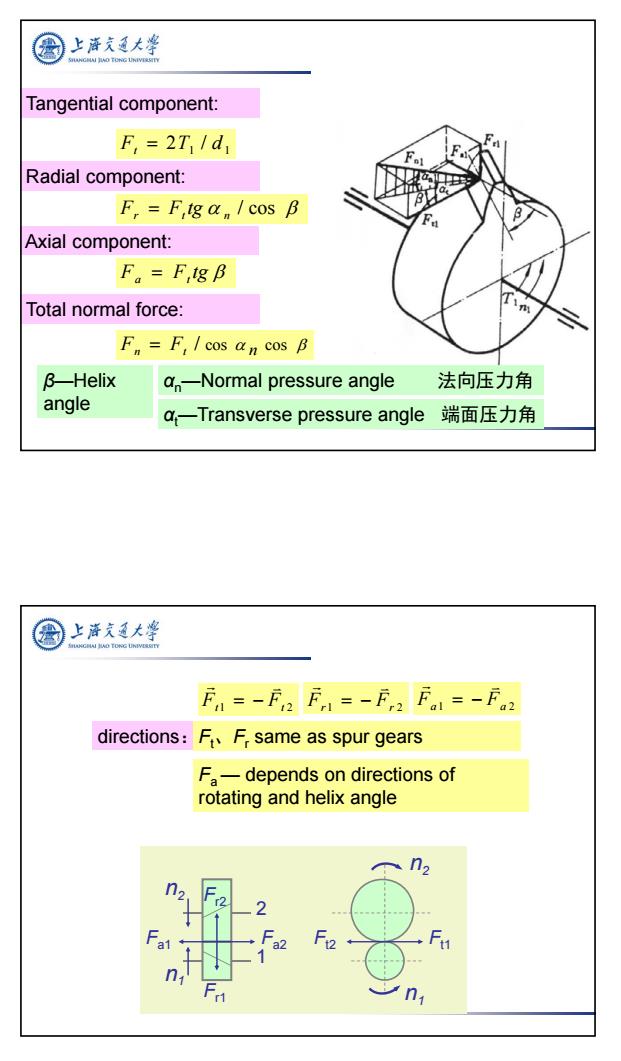
上游久通大学 Tangential component: F,=2T/d1 Radial component: F.F,tg a cos B Axial component: F。=F,gB Total normal force: F=F/cos an cos B B-Helix an-Normal pressure angle 法向压力角 angle a,一Transverse pressure angle端面压力角 上游文大学 f=-F2F,1=-f2F1=-F2 directions:FF same as spur gears Fa-depends on directions of rotating and helix angle F 01
9 Tangential component: 1 1 Ft 2T / d Fr Ft tg n / cos Fa Ft tg / cos cos Fn Ft n αn—Normal pressure angle 法向压力角 αt —Transverse pressure angle 端面压力角 β—Helix angle Radial component: Axial component: Total normal force: 2 1 Ft1 Ft 2 Fr 1 Fr 2 directions:Ft 、Fr same as spur gears Fa — depends on directions of rotating and helix angle Fa1 Fa 2 n2 n1 Fr2 Fr1 Ft2 Ft1 n1 n2 Fa1 Fa2
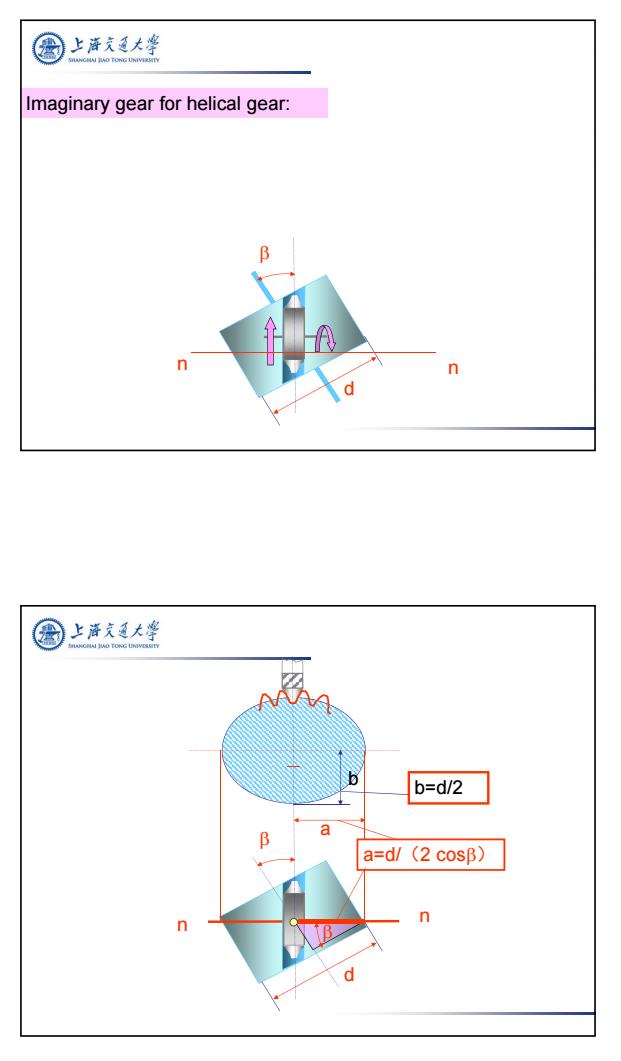
上泽克通大¥ Imaginary gear for helical gear: B 1 n n 上游文大学 ANGHAI HAO TONG UNIVERSITY b=d/2 a B a=d/(2 cosB) n n d
10 d n n Imaginary gear for helical gear: d n n b=d/2 a=d/(2 cos) a b