
高等数学之方向导数
高等数学之

主要内容问题引入2方向导数的定义方向导数的计算S
主要内容 问题引入 方向导数的定义 方向导数的计算 1 2 3

引入计算定义方向导数一、问题引入风云二号气象卫星云图2017年08月01日12:00
一、问题引入 方向导数 引入 定义 计算

引入计算定义方向导数局部地区的等压线问题:风是怎么形成的?一空气流动的结果。问题:方向固定吗?一NO!气压分布函数z=f(x,y)问题:如何刻画二元函数沿不同方向的变化?
局部地区的等压线 问题:风是怎么形成的 ?——空气流动的结果。 问题:方向固定吗? ——NO! 气压分布函数 问题:如何刻画二元函 数沿不同方向的变化? 方向导数 引入 定义 计算
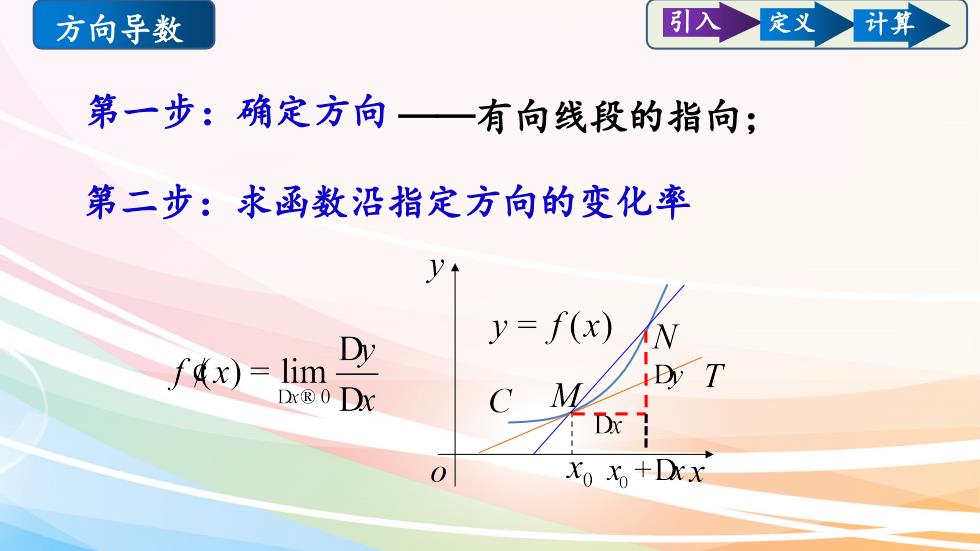
引入计算定义方向导数第一步:确定方向一一有向线段的指向;第二步:求函数沿指定方向的变化率yf(x)V=NDylimfdx)=TDVMDr?ODxCDx-:0Xo Xo+Drx
第一步:确定方向 ——有向线段的指向; 第二步:求函数沿指定方向的变化率 方向导数 引入 定义 计算
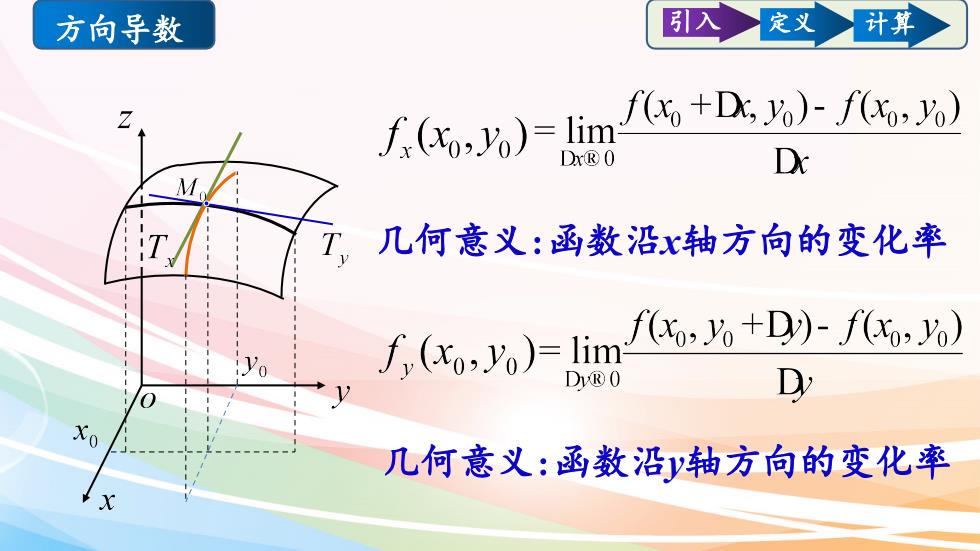
引入计算定义方向导数f(x +Dx, yo)- f(xo, yo)Zf.(xo,yo)= limDxDxR0M几何意义:函数沿x轴方向的变化率f(xo, yo +D)- f(xo, yo)f,(xo, yo)= limVD,DVR 0CXo几何意义:函数沿轴方向的变化率x
几何意义:函数沿x轴方向的变化率 几何意义:函数沿y轴方向的变化率 方向导数 引入 定义 计算

引入计算定义方向导数函数变化率的本质为:函数值的增量与自变量的增量的比值,当自变量的增量趋向于零时的极限,即平均变化率的极限
函数变化率的本质为:函数值的增量与自变量的增 量的比值,当自变量的增量趋向于零时的极限,即 平均变化率的极限。 方向导数 引入 定义 计算

引入计算定义方向导数二、方向导数的定义预备知识:设u=f(x,y,z)在P(xo,Jo,z)的某一邻域内有定义1是以P(xo,yo,zo)为起点的一条射线,P(x,y,z)是I 上任一点,Z1 =(cosu,cosb,cog) P,pl eP(x, y,z)P(xo,yo,z0)x- xo _ y- Jo _ z- Zo =t10cosbcosgcosax
二、方向导数的定义 设 在 的某一邻域内有定义, 是以 为起点的一条射线, 是 上任一点, y x z O 预备知识: 方向导数 引入 定义 计算

引入计算定义方向导数x- xo - y- yo= z- Zo =tcos bcosgcosaZ射线/的参数方程:P(x, y,z)x=xo+tcosaP(xo,Yo, z0)130y=yo+tcosby0L z=zo +tcosgP(x, +tcosa,yo +tcosb, zo +tcosg)RPP=/(x +tcosa - xo) +( +tcosb - y) +(zo +tcosg- z)?三0t3
射线 的参数方程: y x z O 方向导数 引入 定义 计算

引入计算定义方向导数定义:设u=f(x,y,z)在 P(xo,Jo,zo)的某一邻域U(P)内有定义l是以P(xo,Jo,zo)为始点的一条射线,P(x, + tcosa ,y + tcosb,zo + tcosg)是1 上另一点, Pi U(P)函数增量f(x,+tcosa,yo+tcosb,zo+tcosg)-f(xo,Jo,zo)P到P的距离 IPP。I= t
定义:设 在 的某一邻域 为始点的一条射线, 是 上另一点, 是以 内有定义, 函数增量 到 的距离 方向导数 引入 定义 计算