
第二节二重积分的计算法一、利用直角坐标计算二重积分二、利用极坐标计算二重积分
第二节 一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 二重积分的计算法
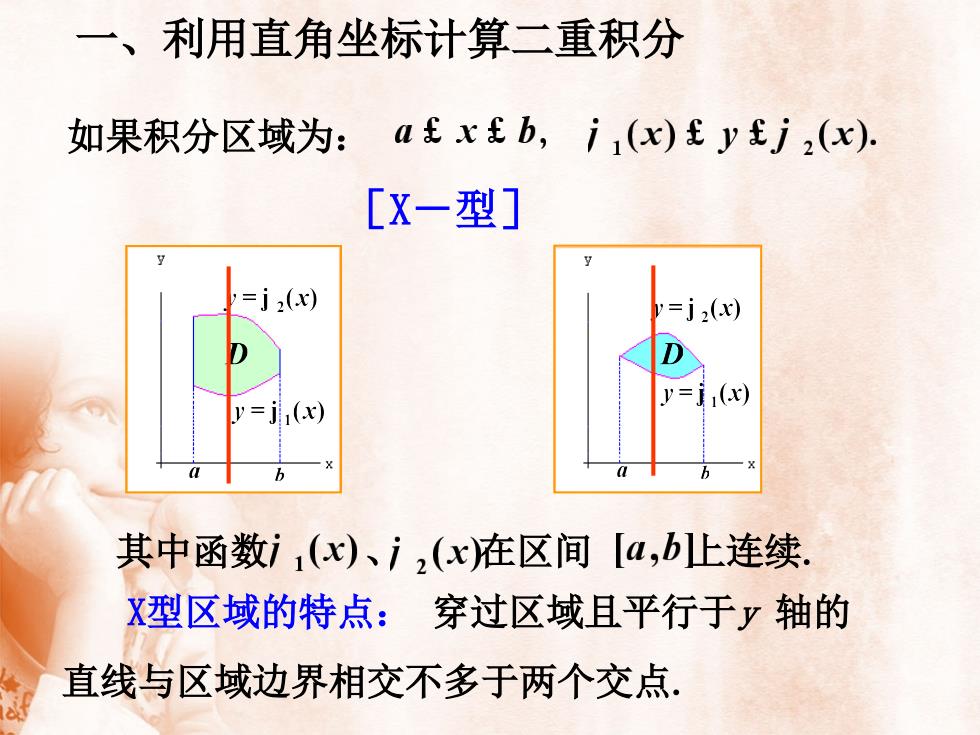
一、利用直角坐标计算二重积分如果积分区域为: ab,i(x)j,(x)[X一型]yC=j2(x)=j2(x)RDy=j(x)y=ji(x)1aabb其中函数i,(x)、i,(x)在区间[a,b上连续X型区域的特点:穿过区域且平行于y轴的直线与区域边界相交不多于两个交点
一、利用直角坐标计算二重积分 如果积分区域为: [X-型] 其中函数 、 在区间 上连续. X型区域的特点: 穿过区域且平行于y 轴的 直线与区域边界相交不多于两个交点
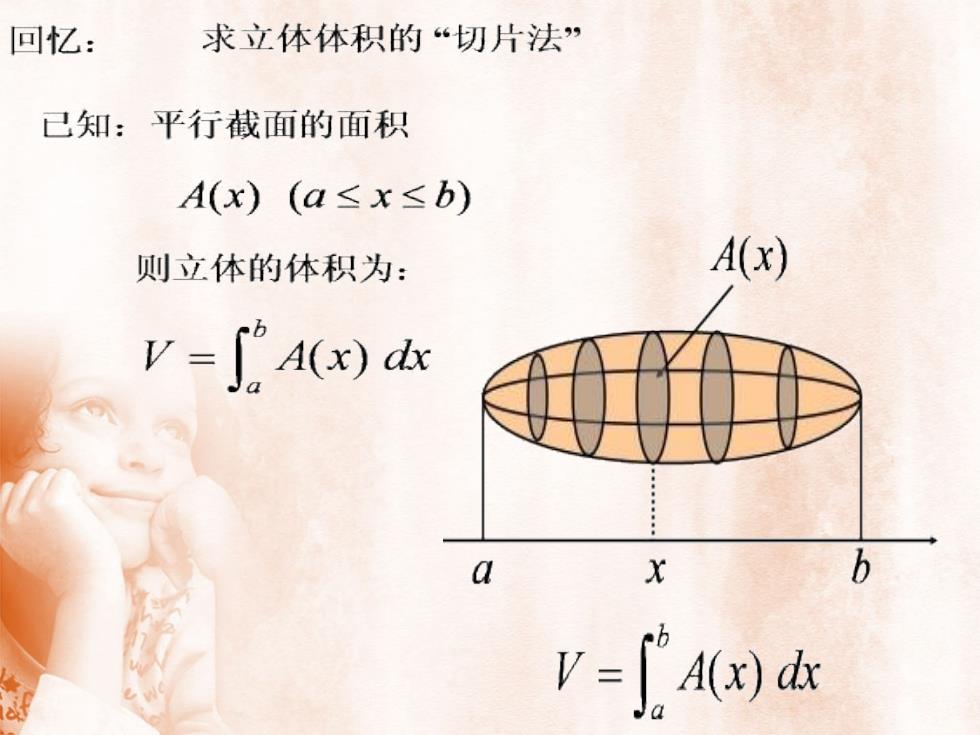
求立体体积的“切片法”回忆:已知:平行截面的面积A(x) (a≤x≤b)A(x)则立体的体积为:V = [A(x) dxbxabV = / A(x) dxJa
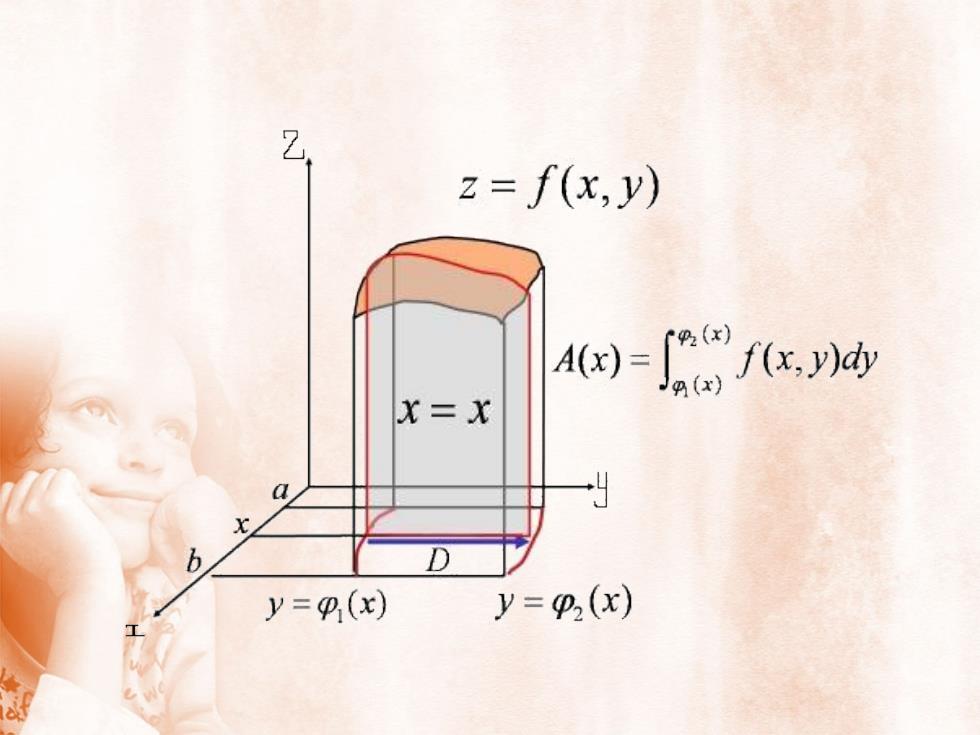
7z= f(x,y)(92(x)f(x,y)dyA(x) =Jg(x)x=x2aXby=p(x)y=p(x)

z= f(x,y)2(x)fydyA(x) =X=xg(x)x视为常数L9(x)P2(x)

(2(x)f(x, y)dyA(x) =(a≤x≤b)Jq(x)6JJ f(x, y)dxdy =V =/A(x) dxJaD(x)-f(x, y)dyl dxag(xrb(92(x)dxf(x,y)dyag(x)

02(x[J f(x, y)dxdy -f(x,y)dydxg(x)Dy=P(x)第一次积分中将x视为常数y=q(x)对积分(偏积分)a

cytd, ii(y)xi,(y)如果积分区域为:[Y一型]Ux=j()x=jl()DDx=i2(y)x=j2(y)nY型区域的特点:穿过区域且平行于x轴的直线与区域边界相交不多于两个交点
如果积分区域为: [Y-型] Y型区域的特点:穿过区域且平行于x 轴的直 线与区域边界相交不多于两个交点
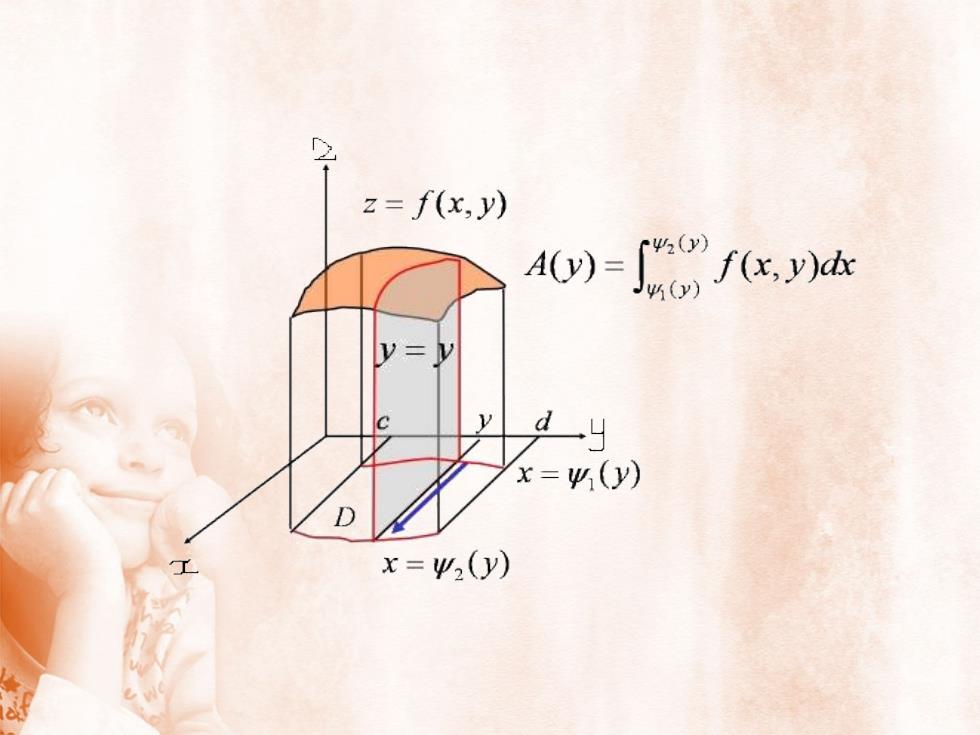
z= f(x,y)42()A(y) =f(x,y)dxy)Vdx=y(y)x=y2(y)工
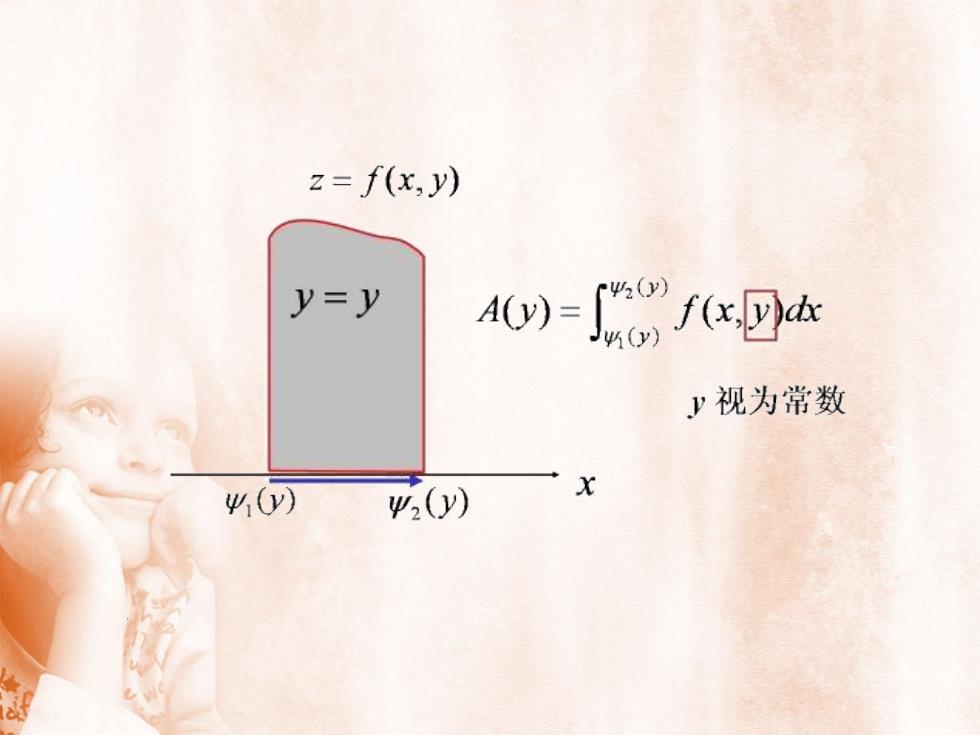
z= f(x,y)2y=yA(y)= Jw f(x,dxKy视为常数xy(y)y,(y)