
第二节平面及其方程
第二节 平面及其方程

曲面方程与空眉间一曲线方程概念
一、曲面方程与空间 曲线方程概念
>曲面方程概念如果曲面s与方程F(x,y,z)=0有下述关系:F(x, y,z)= 0(1)曲面S上的任意点的坐标都满足此方程;(2)不在曲面S上的点的坐标不满足此方程S则F(xy,z)=0叫做曲面S的方程y曲面S叫做方程F(x,y,2)=0的图形>曲线方程概念空间曲线可视为两曲面S,S,的交线F(x,y,z)= 0Si方程组S2G(x, y,z)= 0F(x,y,)=0G(x,y,z) = 0称为空间曲线C的方程曲线C称为方程组的图形
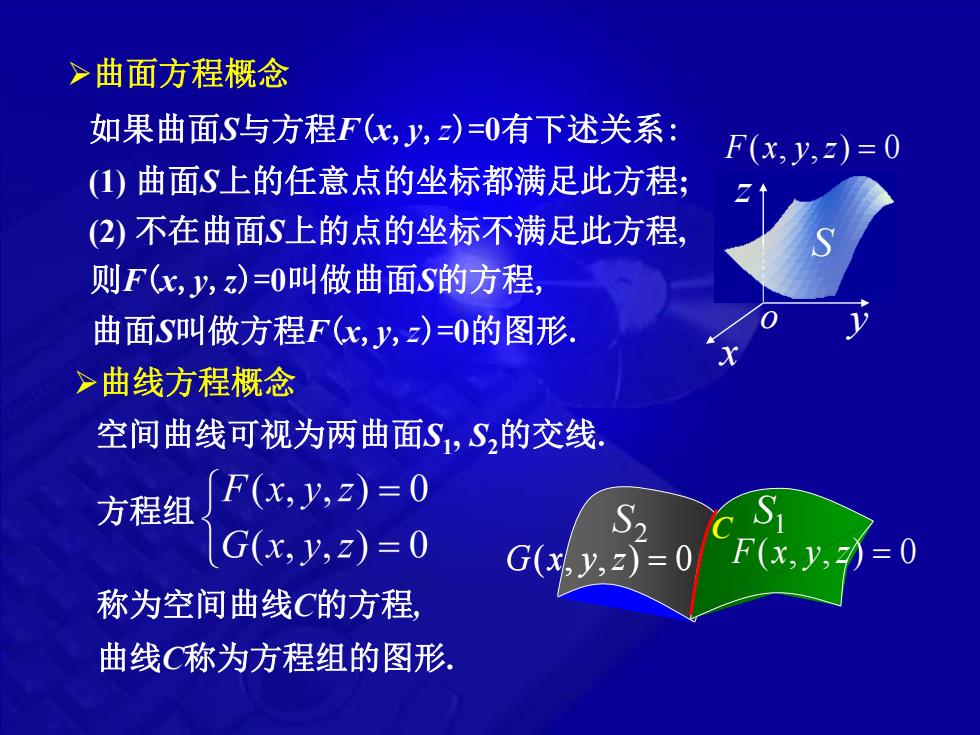
F(x, y,z) 0 S z y x o 如果曲面S与方程F(x,y,z)=0有下述关系: (1) 曲面S上的任意点的坐标都满足此方程; 则F(x,y,z)=0叫做曲面S的方程, 曲面S叫做方程F(x,y,z)=0的图形. (2) 不在曲面S上的点的坐标不满足此方程, 曲面方程概念 曲线方程概念 空间曲线可视为两曲面S1 , S2的交线. S2 G(x, y,z) 0 F(x, y,z) 0 S1 G(x, y,z) 0 方程组 C 称为空间曲线C的方程, 曲线C称为方程组的图形

平面的点法式方程二
二、平面的点法式方程

>方程的建立通过点 M。(xo,Yo,o)设平面ⅡI垂直于非零向量n=(A,BC),法向量任取 M(x,y,z)e II,YMoMInMoM.n=0MoM = (x-Xo,y-yo,z-zoA(x - xo)+ B(y- yo)+C(z - zo) = 0平面Ⅱ的点法式方程
z y x o M0 n ( , , ) 0 0 0 0 通过点 M x y z 垂直于非零向量 ( ) ( ) ( ) 0 A x x0 B y y0 C z z0 M 平面的点法式方程 设平面 M ( x, y,z) , n (A , B, C), M M n 0 0 M 0M n 任取 方程的建立 法向量

A(x-Xo)+B(y-yo)+C(z-zo)=0例1求过点(2,-3,0)以n=(1,-2,3)为法向量的平面方程例2求过三点 M,(2,-1,4), M,(-1,3,-2),M3(0,2,3)的平面Ⅱ的方程
求过三点 的平面的方程. 例2 ( ) ( ) ( ) 0 A x x0 B y y0 C z z0 例1 求过点(2,-3,0)以 为法向量的平面方程

平面的一般方程三
三、平面的一般方程

Ax+By+Cz+D=0(A?+B?+C2+0)>特殊情形D=0, Ax+By+Cz=0通过原点的平面:·A=0,By+Cz+D=0平行于x轴的平面;·A=0,B=0Cz+D=0平行于xoy面的平面;例3求通过x轴和点(4,-3,-1)的平面方程例4用平面的一般式方程导出平面的截距式方程
特殊情形 • D = 0, A x + B y + C z = 0 通过原点的平面; • A = 0, B y + C z + D = 0 • A = 0, B = 0 C z + D = 0 Ax B y C z D 0 ( 0 ) 2 2 2 A B C 平行于x轴的平面; 平行于xoy面的平面; 例3 求通过x轴和点(4,–3,–1)的平面方程. 例4 用平面的一般式方程导出平面的截距式方程

四、两平面的夹角
四、两平面的夹角

两平面法向量的夹角(通常指锐角或直角)称为两平面的夹角ni设平面IⅡI,的法向量为 ni =(Ai,Bi,Cl)n,1O平面II2的法向量为 n, =(A2,B2,C2 则两平面夹角的余弦为nj ·n2IIcOsA=nin2即AiA2 + B;B2 +CiC2cOsO=A?+B? +C2 A2?+B2?+C2
设平面∏1的法向量为 平面∏2的法向量为 则两平面夹角的余弦为 cos 即 A1 A2 B1 B2 C1 C2 2 2 2 2 2 A2 B C 2 1 2 1 2 A1 B C 两平面法向量的夹角(通常指锐角或直角)称为两平面的夹角. 1 2 n2 n1 ( , , ) 1 A1 B1 C1 n ( , , ) 2 A2 B2 C2 n 1 2 1 2 cos n n n n