
密码学是一门交叉学科,涉及到 数论、近世代数、 概率论、组合 逻辑、复杂度理论、操作系统、 算法与数据结构、计算机网络等 多学科知识
密码学是一门交叉学科,涉及到 数论、近世代数、概率论、组合 逻辑、复杂度理论、操作系统、 算法与数据结构、计算机网络等 多学科知识

2.1密码学分类 密码学(Cryptology)是研究信息及 信息系统安全的学科,它起源于保密 通信技术。 密码学又分为密码编码学 (Cryptography)和密码分析学 (Cryptanalysis)
密码学(Cryptology)是研究信息及 信息系统安全的学科,它起源于保密 通信技术。 密码学又分为 密 码 编 码 学 (Cryptography) 和 密 码 分 析 学 (Cryptanalysis)。 2.1 密码学分类

2.1密码学分类 2.1.1密码编码学 密码编码学(Cryptography)是研 究如何对信息编码以实现信息和通 信安全的科学。 密码分析学(Cryptanalysis)是研 究如何破解或攻击受保护的信息的 科学
2.1 密码学分类 ◼ 密码编码学(Cryptography)是研 究如何对信息编码以实现信息和通 信安全的科学。 ◼ 密码分析学(Cryptanalysis)是研 究如何破解或攻击受保护的信息的 科学。 2.1.1 密码编码学
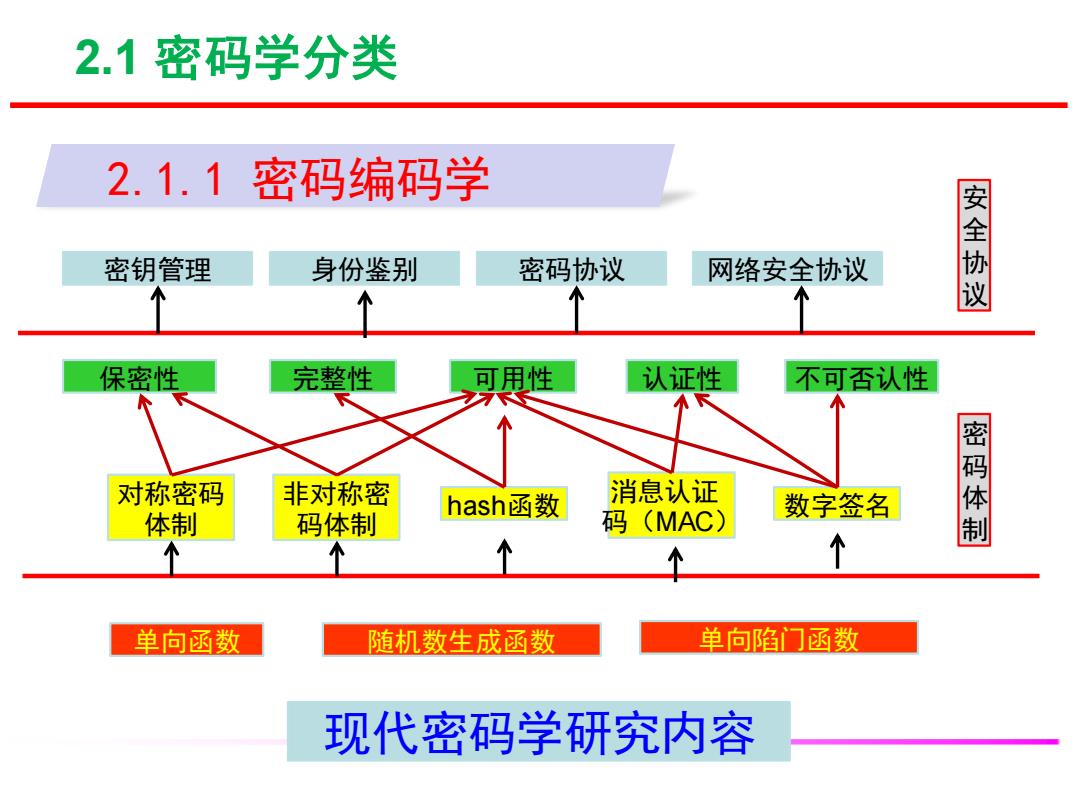
2.1密码学分类 2.1. 1密码编码学 密钥管理 身份鉴别 密码协议 网络安全协议 安全协议 个 保密性 完整性 可用性 认证性 不可否认性 对称密码 非对称密 hash函数 消息认证 数字签名 体制 码体制 码(MAC) 密码体制 个 个 单向函数 随机数生成函数 单向陷门函数 现代密码学研究内容
2.1 密码学分类 2.1.1 密码编码学 密钥管理 身份鉴别 密码协议 网络安全协议 安 全 协 议 保密性 完整性 可用性 认证性 不可否认性 对称密码 体制 非对称密 码体制 hash函数 消息认证 码(MAC) 数字签名 密 码 体 制 单向函数 随机数生成函数 单向陷门函数 现代密码学研究内容

2.1密码学分类 2.1.2 密码分析学 密码分析学(Cryptanalysis)是研究 如何分析和破解各种密码体制的一门 学科。 传统密码学中的加密算法和密钥是不 公开的。而现代密码学的设计与使用 必须遵守科克霍夫原则(Kerckhoffs Principle)
2.1 密码学分类 2.1.2 密码分析学 密码分析学(Cryptanalysis)是研究 如何分析和破解各种密码体制的一门 学科。 传统密码学中的加密算法和密钥是不 公开的。而现代密码学的设计与使用 必须遵守科克霍夫原则(Kerckhoffs Principle)

2.1密码学分类 2.1.2 密码分析学 科克霍夫在其名著《军事密码学》中 关于密码分析的假设:秘密必须完全 寓于秘钥中,即加密和解密算法的安 全性取决于密钥的安全性,而加密、 解密的过程和细节(即算法)是公开 的,只要key是安全的,则攻击者无 法推导出明文
2.1 密码学分类 2.1.2 密码分析学 科克霍夫在其名著《军事密码学》中 关于密码分析的假设:秘密必须完全 寓于秘钥中,即加密和解密算法的安 全性取决于密钥的安全性,而加密、 解密的过程和细节(即算法)是公开 的,只要key是安全的,则攻击者无 法推导出明文

2.1密码学分类 2.1.2 密码分析学 很多密码算法的安全性并没有在理论 上得到严格证明! 密码学家一直也在寻找密码体制安全 性的理论证明方法 目前评价密码体制安全性的两种方法: 无条件安全性和有条件安全性
2.1 密码学分类 2.1.2 密码分析学 很多密码算法的安全性并没有在理论 上得到严格证明! 密码学家一直也在寻找密码体制安全 性的理论证明方法。 目前评价密码体制安全性的两种方法: 无条件安全性和有条件安全性

2.1密码学分类 2.1.2 密码分析学 无条件安全性:对一种密码体制, 无论破解者知道多少密文、采用何 种方法都得不到明文或密钥的信息, 即具有无限计算资源(时间、空间、 设备、资金)的情况下,破解者也 无法破解该密码系统
2.1 密码学分类 2.1.2 密码分析学 ◼ 无条件安全性:对一种密码体制, 无论破解者知道多少密文、采用何 种方法都得不到明文或密钥的信息, 即具有无限计算资源(时间、空间、 设备、资金)的情况下,破解者也 无法破解该密码系统

2.1密码学分类 2.1.2 密码分析学 有条件安全性:是根据破解密码系 统所需的计算量(时间、空间)来 评价其安全性,又称为计算安全性 或实际安全性 。 Shannon在1949年从理论上证明了“一次一密具有完 全保密性”,但现实是真随机密钥很难生成,另外由于 密钥数量与明文数量一样,随着明文数量增长,对密钥 的存储、传输、管理带来了难度
2.1 密码学分类 2.1.2 密码分析学 ◼ 有条件安全性:是根据破解密码系 统所需的计算量(时间、空间)来 评价其安全性,又称为计算安全性 或实际安全性。 Shannon在1949年从理论上证明了“一次一密具有完 全保密性” ,但现实是真随机密钥很难生成,另外由于 密钥数量与明文数量一样,随着明文数量增长,对密钥 的存储、传输、管理带来了难度

2.1密码学分类 2.1.2 密码分析学 计算上的安全性:若破解一个密码 系统是可行的,但使用已知的算法 和现有的计算机不可能完成攻击所 需要的计算量,则称该密码体制是 计算上安全的。 当前的密码体制都属于计算上的安全性 (多数是基于数学难题求解)!
2.1 密码学分类 2.1.2 密码分析学 ◼ 计算上的安全性:若破解一个密码 系统是可行的,但使用已知的算法 和现有的计算机不可能完成攻击所 需要的计算量,则称该密码体制是 计算上安全的。 当前的密码体制都属于计算上的安全性 (多数是基于数学难题求解)!