
Section 2.3 Hash and Message Authentication Code 1
1 Section 2.3 Hash and Message Authentication Code
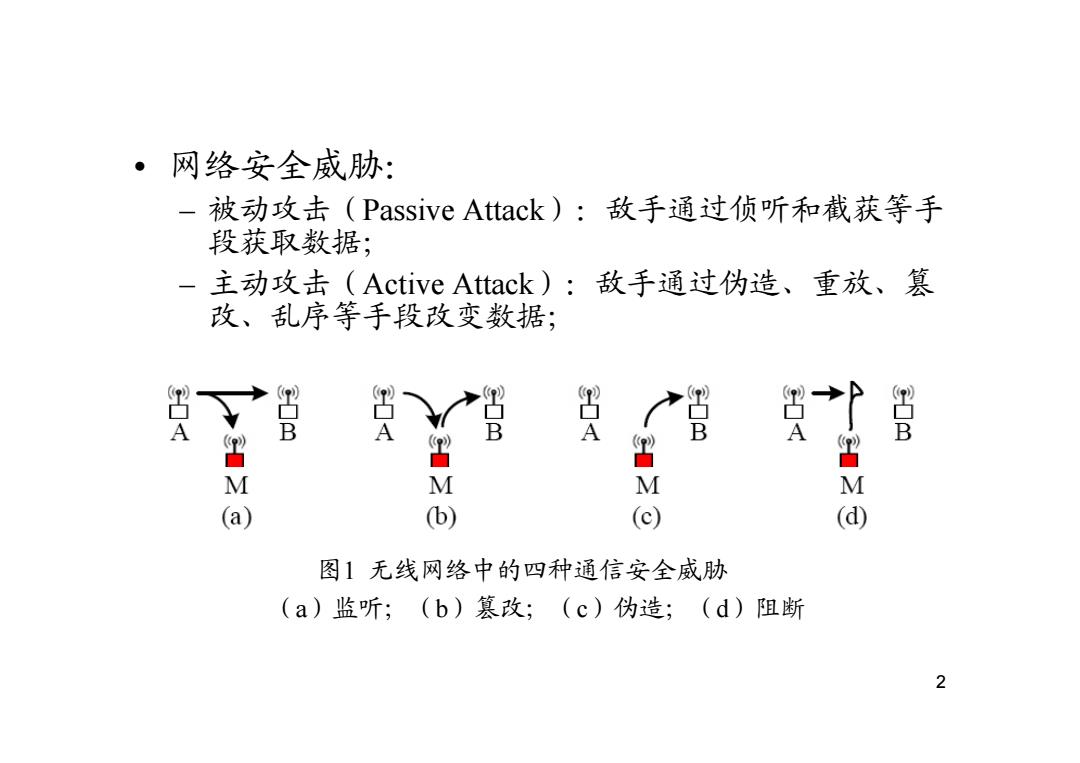
·网络安全威胁: -被动攻击(Passive Attack):敌手通过侦听和截获等手 段获取数据; 主动攻击(Active Attack):敌手通过伪造、重放、篡 改、乱序等手段改变数据; 30 Gm 罩 c0m 30d 管 COm M 3o 30Z a (b) (c) (d 图1无线网络中的四种通信安全威胁 (a)监听;(b)篡改;(c)伪造;(d)阻断 2
• 网络安全威胁: – 被动攻击(Passive Attack Passive Attack):敌手通过侦听和截获等手 敌手通过侦听和截获等手 段获取数据; – 主动攻击(Active Attack):敌手通过伪造、重放、篡 改、乱序等手段改变数据; (a)监听;(b)篡改;(c)伪造;(d)阻断 图1 无线网络中的四种通信安全威胁 2

·消息认证(Message Authentication)的目的: 一验证消息的完整性,确认数据在传送和存储过程中未 受到主动攻击。 ·消息认证的方式: 一消息加密函数:加密整个消息,以消息的密文文件作 为认证,可使用对称密码或公钥密码体制进行加密; -散列函数(Hash):将任意长度的消息变换为定长的 消息摘要,并加以认证; -消息认证码(MAC):依赖公开的函数(密钥控制下) 对消息处理,生成定长的认证标识,并加以认证; 3
• 消息认证(Message Authentication)的目的: – 验证消息的完整性,确认数据在传送和存储过程中未 受到主动攻击。 • 消息认证的方式: – 消息加密函数:加密整个消息,以消息的密文文件作 以消息的密文文件作 为认证,可使用对称密码或公钥密码体制进行加密; – 散列函数(Hash):将任意长度的消息变换为定长的 消息摘要,并加以认证; – 消息认证码(MAC):依赖公开的函数(密钥控制下) 对消息处理,生成定长的认证标识 生成定长的认证标识,并加以认证; 3

提纲 ·1散列函数 一1.1散列函数的定义 -1.2散列函数的通用结构 -1.3MD5 ·2消息认证码 -2.1MAC函数 -2.2MAC的安全性 -2.3 CBC-MAC 4
提纲 • 1 散列函数 – 1.1 散列函数的定义 – 1.2 散列函数的通用结构 – 1.3 MD5 • 2 消息认证码 – 2 1 MAC 2.1 MAC函数 – 2.2 MAC的安全性 – 2 3. CBC-MAC 4

提纲 ·1散列函数 -1.1散列函数的定义 -1.2散列函数的通用结构 -1.3MD5 ·2消息认证码 5
提纲 • 1 散列函数 – 1.1 散列函数的定义 – 1.2 散列函数的通用结构 – 1 3 MD5 1.3 MD5 • 2 消息认证码 5

散列函数的定义 ·散列函数H是一个公开的函数,它将任意长度的消息M变换为固定长 度的散列码h。 。h=H() -M:变长消息,H():定长的散列值 。 散列函数是一种算法,算法的输出内容称为散列码或者消息摘要。 ·消息摘要要唯一地对应原始消息,如果原始消息改变并且再次通过散 列函数,它将生成不同的消息摘要,,因此散列函数能用来检测消息地 完整性,保证消息从建立开始到收到为止没有被改变和破坏。 ● 运行相同算法的接受者应该收到系统的消息摘要,否则保温是不可信 的。 散列函数又称为:哈希(Hash)函数、数字指纹(Digital fingerprint)、压缩(Compression)函数、数据认证码(Data Authentication Code 6
散列函数的定义 • 散列函数 H 是一个公开的函数,它将任意长度的消息 它将任意长度的消息 M变换为固定长 度的散列码 h 。 • h = H (M) – M:变长消息, H(M):定长的散列值 • 散列函数是一种算法 散列函数是一种算法,算法的输出内容称为 算法的输出内容称为散列码或者消息摘要。 • 消息摘要要唯一地对应原始消息,如果原始消息改变并且再次通过散 列函数,它将生成不同的消息摘要,因此散列函数能用来检测消息地 完整性,保证消息从建立开始到收到为止没有被改变和破坏。 • 运行相同算法的接受者应该收到系统的消息摘要,否则保温是不可信 的。 • 散列函数又称为:哈希( Hash )函数、数字指纹(Digital fingerprint)、压缩(Compression)函数、数据认证码(Data Authentication Code)等 6

散列函数的要求 ·H能用于任意大小的分组; ·H能产生定长的输出; 0 对任何给定的x,H(x)要相对易于计算,使得硬件和软件 实现成为实际可能; 0 对任何给定的码h,寻找x使得H(x)=h在计算上是不可 行的,即单向性(one-way); 对任意给定的分组x,寻找不等于x的y,使得Hx)=Hy) 在计算上是不可行的,即弱抗冲突性(Weak Collision-free); ·寻找对任意的(x,y)对使得Hx)=Hy)在计算上是不可行 的,即强抗冲突性(Strong Collision-free; 7
散列函数的要求 • H 能用于任意大小的分组; • H 能产生定长的输出; • 对任何给定的 x,H(x )要相对易于计算,使得硬件和软件 实现成为实际可能; • 对任何给定的码 h ,寻找 x 使得 H(x ) =h 在计算上是不可 行的,即单向性 (one-way); • 对任意给定的分组 x,寻找不等于x 的 y,使得 H(x ) = H(y ) 在计算上是不可行的 在计算上是不可行的,即弱抗冲突性 (Weak Collision Weak Collision -free); • 寻找对任意的 (x, y) 对使得 H(x ) =H (y) 在计算上是不可行 的,即强抗冲突性 (Strong Collision-free); 7

提纲 ·1散列函数 -1.1散列函数的定义 -1.2散列函数的通用结构 -1.3MD5 ·2消息认证码 8
提纲 • 1 散列函数 – 1.1 散列函数的定义 – 1.2 散列函数的通用结构 – 1 3 MD5 1.3 MD5 • 2 消息认证码 8

2.2Hash函数的通用结构 ·由Ron Rivest于1990年提出MD4 ·几乎被所有Hash函数使用 ·具体做法: -把原始消息M分成一些固定长度的块Y, -最后一块padding并使其包含消息M长度 -设定初始值CV。 -压缩函数方CV,=f(CV,Y1) -最后一个CV,为Hash值 9
2.2 Hash函数的通用结构 函数的通用结构 • 由R Ri onvest于1990年提出MD4 • 几乎被所有Hash函数使用 • 具体做法: – 把原始消息M分成一些固定长度的块Yi – 最后一块 padding 并使其包含消息M长度 – 设定初始值CV0 – 压缩函数 f CVi=f (CVi 1 Yi 1 压缩函数 f, CV ) i=f (CVi-1, Yi-1) – 最后一个 CVi 为Hash值 9

General Structure of Secure Hash Code YL-I CV CVo=IV=initial n-bit value CVi=f(CVi-,Yi1) (1≤i≤L) IV=initial value初始值 H(M)=CVL CV=chaining value链接值 Yi=ith input block(第i个输入数据块) f-compression algorithm(压缩算法) n=length of hash code(散列码的长度) b=length of input block(输入块的长度) 10
10