
编程任务要求 编程语言为C语言或其它语言,要求提交加密、 解密、破解源代码文件。 实现对任意有意义的英文文本文件(*.txt)的 Virginia加密、解密算法,其中秘钥是任意输 入的一个字符串。要求提供明文文本文件、密 文文本文件。 在不知道秘钥的情况下,对一个用Virginia加 密算法生成的密文文本文件进行破解,包括破 解秘钥、生成对应的明文。要求提供程序测试 说明文档
编程任务要求 • 编程语言为C语言或其它语言,要求提交加密、 解密、破解源代码文件。 • 实现对任意有意义的英文文本文件(*.txt)的 Virginia加密、解密算法,其中秘钥是任意输 入的一个字符串。要求提供明文文本文件、密 文文本文件。 • 在不知道秘钥的情况下,对一个用Virginia加 密算法生成的密文文本文件进行破解,包括破 解秘钥、生成对应的明文。要求提供程序测试 说明文档

Virginia加密算法、解密算法
Virginia加密算法、解密算法

Virginia加密算法 ·假设语言的字符集为 Charset[26]=a','b',...'z' 字符集大小=26 ·对应的字符编码为 C0ding[26]={0,1,,25}
Virginia加密算法 • 假设语言的字符集为 Charset[26]={‘a’, ’b’, …, ’z’} 字符集大小=26 • 对应的字符编码为 Coding[26]={0, 1, …, 25}

Virginia加密算法 ·Virginia加密算法是对明文进行加密的 过程中依照密钥的指示轮流使用多个 单表代替密码。 ·设明文串为: M=mm2.mn,m,∈charset,,n是明文长度 ·秘钥为: K=kk2.ka,k,∈charset,.d是秘钥长度 ·密文为: C=CC2.Cn,C,∈charset,n是密文长度
Virginia加密算法 • Virginia加密算法是对明文进行加密的 过程中依照密钥的指示轮流使用多个 单表代替密码。 • 设明文串为: M=m1m2…mn,mi∈charset, n是明文长度 • 秘钥为: K=k1 k2…kd,ki∈charset, d是秘钥长度 • 密文为: C=c1 c2…cn,ci∈charset, n是密文长度

Virginia加密算法 ·加密算法: Cjtu(mitid+ki mod 26 j=1...d,t-0...ceiling(n/d)-1 其中ceiling(x)函数表示不小于x最小整数 解密算法: mjtud-(cita-ki)mod 26 j=1...d,t=0...ceiling(n/d)-1 其中ceiling()函数表示不小于x最小整数
Virginia加密算法 • 加密算法: cj+td=(mj+td+kj ) mod 26 j=1…d, t=0…ceiling(n/d)-1 其中ceiling(x)函数表示不小于x最小整数 • 解密算法: mj+td=(cj+td -kj ) mod 26 j=1…d, t=0…ceiling(n/d)-1 其中ceiling(x)函数表示不小于x最小整数
Virginia加密算法举例 ml m2 m3 m4 m5 m6 m7 m8 m9 ml0 mll 明文M n 0 t h n g i S 0 (编码) (13) (14) (19) (7) (8) (13) (8) (18) (19) (14) 秘钥K j y 0 y y 0 (编码) (9) (14) (24) (9) (14) (24) (9 (14) (24) (9 (14) 密文C r W p W c (编码) (22) (2) (17) (16) (22) (11) (15) (22) (16) (2) (2) j=1j=2j=3 j=1j=2j=3 j=1j=2j=3 j护1 j=2 t=0t=0 =0t=1t=1t=1t=2t=2t=2 t=3 t=3 明文长度n=11,秘钥长度d=3, ceiling(11/3)-1=3
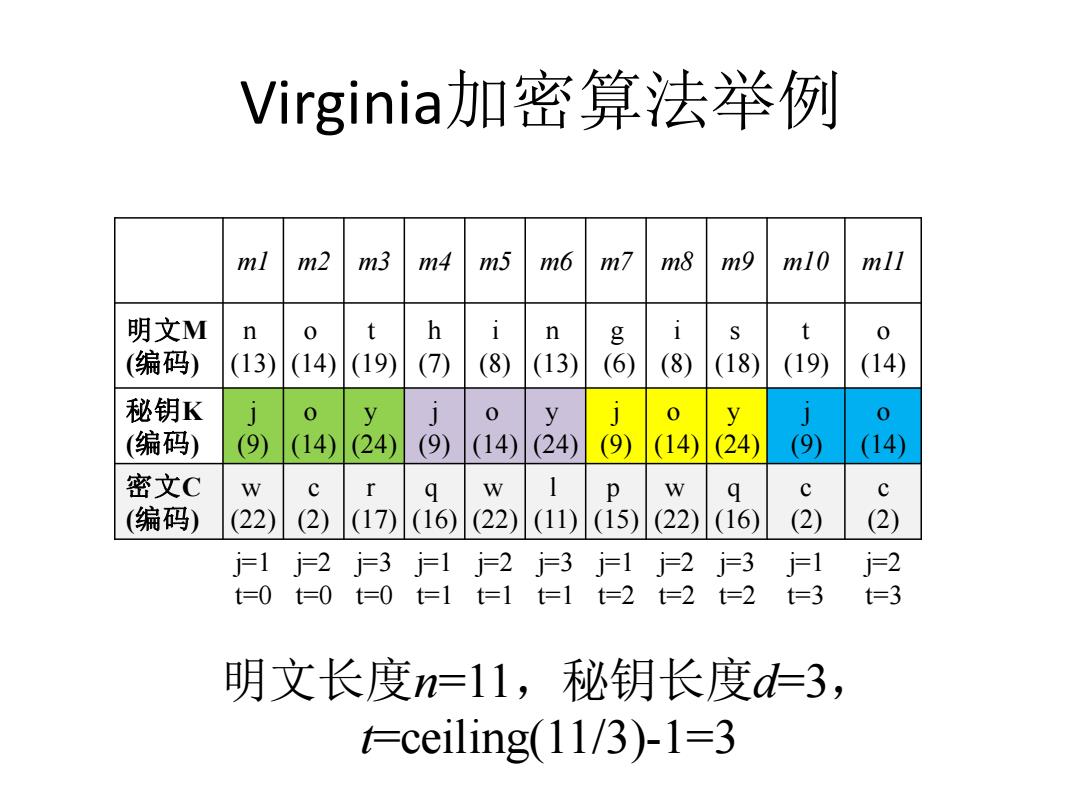
Virginia加密算法举例 m1 m2 m3 m4 m5 m6 m7 m8 m9 m10 m11 明文M (编码) n (13) o (14) t (19) h (7) i (8) n (13) g (6) i (8) s (18) t (19) o (14) 秘钥K (编码) j (9) o (14) y (24) j (9) o (14) y (24) j (9) o (14) y (24) j (9) o (14) 密文C (编码) w (22) c (2) r (17) q (16) w (22) l (11) p (15) w (22) q (16) c (2) c (2) j=1 t=0 j=2 t=0 j=3 t=0 j=1 t=1 j=2 t=1 j=3 t=1 j=1 t=2 j=2 t=2 j=3 t=2 j=1 t=3 j=2 t=3 明文长度n=11,秘钥长度d=3, t=ceiling(11/3)-1=3

一个原始的明文文本 Differential Privacy is the state-of-the-art goal for the problem of privacy-preserving data release and privacy-preserving data mining.Existing techniques using differential privacy,however, cannot effectively handle the publication of high-dimensional data.In particular,when the input dataset contains a large number of attributes,existing methods incur higher computing complexity and lower information to noise ratio,which renders the published data next to useless. This proposal aims to reduce computing complexity and signal to noise ratio.The starting point is to approximate the full distribution of high-dimensional dataset with a set of low-dimensional marginal distributions via optimizing score function and reducing sensitivity,in which generation of noisy conditional distributions with differential privacy is computed in a set of low-dimensional subspaces,and then,the sample tuples from the noisy approximation distribution are used to generate and release the synthetic dataset.Some crucial science problems would be investigated below:(i)constructing a low k-degree Bayesian network over the high-dimensional dataset via exponential mechanism in differential privacy,where the score function is optimized to reduce the sensitivity using mutual information,equivalence classes in maximum joint distribution and dynamic programming;(ii)studying the algorithm to compute a set of noisy conditional distributions from joint distributions in the subspace of Bayesian network,via the Laplace mechanism of differential privacy.(iii)exploring how to generate synthetic data from the differentially private Bayesian network and conditional distributions,without explicitly materializing the noisy global distribution.The proposed solution may have theoretical and technical significance for synthetic data generation with differential privacy on business prospects
一个原始的明文文本 Differential Privacy is the state-of-the-art goal for the problem of privacy-preserving data release and privacy-preserving data mining. Existing techniques using differential privacy, however, cannot effectively handle the publication of high-dimensional data. In particular, when the input dataset contains a large number of attributes, existing methods incur higher computing complexity and lower information to noise ratio, which renders the published data next to useless. This proposal aims to reduce computing complexity and signal to noise ratio. The starting point is to approximate the full distribution of high-dimensional dataset with a set of low-dimensional marginal distributions via optimizing score function and reducing sensitivity, in which generation of noisy conditional distributions with differential privacy is computed in a set of low-dimensional subspaces, and then, the sample tuples from the noisy approximation distribution are used to generate and release the synthetic dataset. Some crucial science problems would be investigated below: (i) constructing a low k-degree Bayesian network over the high-dimensional dataset via exponential mechanism in differential privacy, where the score function is optimized to reduce the sensitivity using mutual information, equivalence classes in maximum joint distribution and dynamic programming; (ii)studying the algorithm to compute a set of noisy conditional distributions from joint distributions in the subspace of Bayesian network, via the Laplace mechanism of differential privacy. (iii)exploring how to generate synthetic data from the differentially private Bayesian network and conditional distributions, without explicitly materializing the noisy global distribution. The proposed solution may have theoretical and technical significance for synthetic data generation with differential privacy on business prospects

经过预处理之后的明文文本 (只保留字符集中的字符) differentialprivacyisthestateoftheartgoalfortheproblemofprivacypreservingdatarelease andprivacypreservingdataminingexistingtechniquesusingdifferentialprivacyhoweverca nnoteffectivelyhandlethepublicationofhighdimensionaldatainparticularwhentheinputd atasetcontainsalargenumberofattributesexistingmethodsincurhighercomputingcomple xityandlowerinformationtonoiseratiowhichrendersthepublisheddatanexttouselessthisp roposalaimstoreducecomputingcomplexityandsignaltonoiseratiothestartingpointistoap proximatethefulldistributionofhighdimensionaldatasetwithasetoflowdimensionalmargi naldistributionsviaoptimizingscorefunctionandreducingsensitivityinwhichgenerationof noisyconditionaldistributionswithdifferentialprivacyiscomputedinasetoflowdimensiona Isubspacesandthenthesampletuplesfromthenoisyapproximationdistributionareusedto generateandreleasethesyntheticdatasetsomecrucialscienceproblemswouldbeinvestiga tedbelowiconstructingalowkdegreebayesiannetworkoverthehighdimensionaldatasetvi aexponentialmechanismindifferentialprivacywherethescorefunctionisoptimizedtoredu cethesensitivityusingmutualinformationequivalenceclassesinmaximumjointdistributio nanddynamicprogrammingiistudyingthealgorithmtocomputeasetofnoisyconditionaldis tributionsfromjointdistributionsinthesubspaceofbayesiannetworkviathelaplacemechan ismofdifferentialprivacyiiiexploringhowtogeneratesyntheticdatafromthedifferentiallypr ivatebayesiannetworkandconditionaldistributionswithoutexplicitlymaterializingthenois yglobaldistributiontheproposedsolutionmayhavetheoreticalandtechnicalsignificancefo rsyntheticdatagenerationwithdifferentialprivacyonbusinessprospects
经过预处理之后的明文文本 (只保留字符集中的字符) differentialprivacyisthestateoftheartgoalfortheproblemofprivacypreservingdatarelease andprivacypreservingdataminingexistingtechniquesusingdifferentialprivacyhoweverca nnoteffectivelyhandlethepublicationofhighdimensionaldatainparticularwhentheinputd atasetcontainsalargenumberofattributesexistingmethodsincurhighercomputingcomple xityandlowerinformationtonoiseratiowhichrendersthepublisheddatanexttouselessthisp roposalaimstoreducecomputingcomplexityandsignaltonoiseratiothestartingpointistoap proximatethefulldistributionofhighdimensionaldatasetwithasetoflowdimensionalmargi naldistributionsviaoptimizingscorefunctionandreducingsensitivityinwhichgenerationof noisyconditionaldistributionswithdifferentialprivacyiscomputedinasetoflowdimensiona lsubspacesandthenthesampletuplesfromthenoisyapproximationdistributionareusedto generateandreleasethesyntheticdatasetsomecrucialscienceproblemswouldbeinvestiga tedbelowiconstructingalowkdegreebayesiannetworkoverthehighdimensionaldatasetvi aexponentialmechanismindifferentialprivacywherethescorefunctionisoptimizedtoredu cethesensitivityusingmutualinformationequivalenceclassesinmaximumjointdistributio nanddynamicprogrammingiistudyingthealgorithmtocomputeasetofnoisyconditionaldis tributionsfromjointdistributionsinthesubspaceofbayesiannetworkviathelaplacemechan ismofdifferentialprivacyiiiexploringhowtogeneratesyntheticdatafromthedifferentiallypr ivatebayesiannetworkandconditionaldistributionswithoutexplicitlymaterializingthenois yglobaldistributiontheproposedsolutionmayhavetheoreticalandtechnicalsignificancefo rsyntheticdatagenerationwithdifferentialprivacyonbusinessprospects

经过virginia加密后的密文 加密秘钥key=infosec lvktwvgvgnodttqifqqmubujglevmbkhziczglcsphweyvwttwoqseshxenjsgaxejgwvxqalrsxczrqsswgiaid jmxipddjiumeawfkfigfaarkvtjlawvqalhwgjvwiwwwavsuvmhnrwsfxkiyufazckImcoixmehofrqbrktwg vqijzqlcvqqsllgxhgzagcbvtbgjjqtmraqgvfncfenInyoarriey wuyniebvwrvprnbhyvInyokivkbshsmpanqo jkgvhrpwvqnnyhjmdcgjgwbkagnbyqgbutrkmpkhwvakjmehcetwbvsuusoxyjlaxaiaizgagzvstgvoigncf xqvbngwvcbvtkzmepejbvitagmshydtvxvwhfigfbwbvbbzgwpgafyvawrzbuckenivrglstmqzqwgquczha rikbrddizqgdofhuqtsodxqvbngwvcbvthziubnwharixbnblmubbfdhvqfvrolivprkidpfqfyfafwbvtbgjjqt mraqgvfncfenInyokivevyvswgbbkzgafqzjbkmqvnqasviqafzvmubenpmxkwaxjaeqxgnaadkvtxqgvgnh sqlmqvnsrjifcpnbywgvfnhazkbInbolkkulsfitigncfshvbngqgqvqnhaspiyiwkxtqozhaspajnhzhknsjfwrv qnqdjmxipdwkgquczhwhkvnxslshtbbraqgvfncfenahggheemffbvxjmayvwwcucqslyrtrxtjsobujbgmu gnudjszqzfhasplvxhjmdcgncfetmhxsvxqorssjevmnsrjinmnxsllgalshzivqpioleumgxceiezhhwspukvjbu irzbgzwquebzzvfgqaaskxkonysvfgtbbwuspagwiuxkvtfzgamIrlfwidiljgaepvrykgvmwijfllgpvlwvmomax wgrctqfhswgbinowbrwajblmctzjqzepqfrwfhknsjfwrvqnqdjmxipdkzitmgmskgqzrkifgvqbswksrbvrwr ifbbwsvyemgmskipavywnmvghxwfkocgzodmpnbwasxkwajemmxiyjbuietnxgwwkvzflaqwuwtwfxfqf yfafwbvtbsrfllsoemexetujeouvsuamubhimaribujodkqzvyvexqkbrdmxgifjhgjpwvxmusplvywgrctqng lvkjhywgrunetabskvgiwkxtqozhaspavshziucoxdsggwsgoqiuqnsbwxywepjaevprqohpckrrsulcvvxagjf qsksjipbvfzhvkdnhmamkmkuzgvkvtmcoxqorssjevmfdbllgbvhrsxcnetallglvktwvgvgnodpaxenjsxgjnd skmcvajhostsnsrusplvywgrctqnglvkjhywgruevyvgyvmkuzagkbydasxgzvfzadkvtyvwrqqfdudsdiyiwkx tqozhaspbujdjsrwfjrksncgncfqcgufjwxjmbwslmeiyfbvxgkuswuenavlbajkknsqwjqzfdbllgbvhrsxcorss jevqbskaxjlvktwvgvgnodttqifqqspjhxwfiuacwcktgkgxvzlj
经过virginia加密后的密文 加密秘钥key=infosec lvktwvgvgnodttqifqqmubujglevmbkhziczglcsphweyvwttwoqseshxenjsgaxejgwvxqalrsxczrqsswgiaid jmxipddjiumeawfkfigfaarkvtjlawvqalhwgjvvviwwwavsuvmhnrwsfxkiyufazcklmcoixmehofrqbrktwg vqijzqlcvqqsllgxhgzagcbvtbgjjqtmraqgvfncfenlnyoarrieywuyniebvwrvprnbhyvlnyokivkbshsmpanqo jkgvhrpwvqnnyhjmdcgjgwbkagnbyqgbutrkmpkhwvakjmehcetwbvsuusoxyjlaxaiaizgagzvstgvoigncf xqvbngwvcbvtkzmepejbvitagmshydtvxvwhfigfbwbvbbzgwpgafyvawrzbuckenivrglstmqzqwgquczha rikbrddizqgdofhuqtsodxqvbngwvcbvthziubnwharixbnblmubbfdhvqfvrolivprkidpfqfyfafwbvtbgjjqt mraqgvfncfenlnyokivevyvswgbbkzgafqzjbkmqvnqasviqafzvmubenpmxkwaxjaeqxgnaadkvtxqgvgnh sqlmqvnsrjifcpnbywgvfnhazkblnbolkkulsfitigncfshvbngqgqvqnhaspiyiwkxtqozhaspajnhzhknsjfwrv qnqdjmxipdwkgquczhwhkvnxslshtbbraqgvfncfenahggheemffbvxjmayvwwcucqslyrtrxtjsobujbgmu gnudjszqzfhasplvxhjmdcgncfetmhxsvxqorssjevmnsrjinmnxsllgalshzivqpioleumgxceiezhhwspukvjbu irzbgzwquebzzvfgqaaskxkonysvfgtbbwuspagwiuxkvtfzgamlrlfwidiljgaepvrykgvmwijfllgpvlvvmomax wgrctqfhswgbinowbrwajblmctzjqzepqfrwfhknsjfwrvqnqdjmxipdkzitmgmskgqzrkifgvqbswksrbvrwr ifbbwsvyemgmskipavywnmvghxwfkocgzodmpnbwasxkwajemmxiyjbuietnxgwwkvzflaqwuwtwfxfqf yfafwbvtbsrfllsoemexetujeouvsuamubhimaribujodkqzvyvexqkbrdmxgifjhgjpwvxmusplvywgrctqng lvkjhywgrunetabskvgiwkxtqozhaspavshziucoxdsggwsgoqiuqnsbwxywepjaevprqohpckrrsulcvvxagjf qsksjipbvfzhvkdnhmamkmkuzgvkvtmcoxqorssjevmfdbllgbvhrsxcnetallglvktwvgvgnodpaxenjsxgjnd skmcvajhostsnsrusplvywgrctqnglvkjhywgruevyvgyvmkuzagkbydasxgzvfzadkvtyvwrqqfdudsdiyiwkx tqozhaspbujdjsrwfjrksncgncfqcgufjwxjmbwslmeiyfbvxgkuswuenavlbajkknsqwjqzfdbllgbvhrsxcorss jevqbskaxjlvktwvgvgnodttqifqqspjhxwfiuacwcktgkgxvzlj

Virginia加密秘钥的破解 一一唯密文攻击
Virginia加密秘钥的破解 ——唯密文攻击