
Section 2.4 Public Key Cryptosystem
Section 2.4 Public Key Cryptosystem

本讲主要内容 。公钥密码体制的简介 。背包问题 ORSA算法 。ElGama算法 。ECC算法 。IBE算法 3 CNR@HEU http://machunguang.hrbeu.edu.cn
本讲主要内容 公钥密码体制的简介 背包问题 RSA算法 ElGamal算法 ECC算法 IBE算法 3

回顾 保密通信进入计算机网络时代,传统密码体制逐渐暴露其 固有的弱点,当时主要体现密钥管理。 。1976年W.Diffie和He11man在《密码学的新方向》中首次 提出了公钥密码算法的思想。 01 978年后Rivest,Shamir和Adleman:提出的RSA算法体现了 公钥算法的思想,并具有实用性。 。公钥密码体制是现代密码学的一个标志,到目前为止,是 密码学史上最大也是唯一真正的革命。 。公钥密码引起密码界高度关注,并得到迅速的发展,尤其 在信息安全的应用中涉及公钥密码技术。 CNR@HEU http://machunguang.hrbeu.edu.cn
回顾 保密通信进入计算机网络时代 计算机网络时代,传统密码体制逐渐暴露其 传统密码体制逐渐暴露其 固有的弱点,当时主要体现密钥管理。 1976年W.Diffie和H ll e man 在《密码学的新方向 密码学的新方向》中首次 提出了公钥密码算法的思想。 1978年后Rivest,Shamir和Adleman Adleman提出的RSA算法体现了 公钥算法的思想,并具有实用性。 公钥密码体制是现代密码学的一个标志,到目前为止,是 密码学史上最大也是唯 密码学史上最大也是唯 真正的革命 一 。 公钥密码引起密码界高度关注,并得到迅速的发展,尤其 在信息安全的应用中涉及公钥密码技术 4 在信息安全的应用中涉及公钥密码技术

引言 在公钥密码体制以前的整个密码学发展史中,所有的密码 算法,包括原始手工计算的、由机械设备实现的以及由计算机 实现的,都是基于代换和换位这两个基本方法,建立在位(字 符)方式的操作上。 而公钥密码体制则为密码学的发展提供了新的理论和技术 思想,一方面公钥密码算法是建立在数学函数基础上的,而不 是建立在位(字符)方式的操作上的;另一方面公钥密码算法是 以非对称的形式使用两个密钥,两个密钥的使用对密钥分配、 认证等都有着深刻的意义。可以说,公钥密码体制的出现在密 码学发展史上是一次质的飞跃。 5 CNR@HEU http://machunguang.hrbeu.edu.cn
引言 在公钥密码体制以前的整个密码学发展史中,所有的密码 算法,包括原始手工计算的、由机械设备实现的以及由计算机 实现的,都是基于代换和换位这两个基本方法 这两个基本方法,建立在位(字 符)方式的操作上。 而公钥密码体制则为密码学的发展提供了新的理论和技术 思想,一方面公钥密码算法是建立在 公钥密码算法是建立在数学函数基础上的,而不 是建立在位(字符)方式的操作上的 ;另一方面公钥密码算法是 ;另一方面公钥密码算法是 以非对称的形式使用两个密钥,两个密钥的使用对密钥分配、 认证等都有着深刻的意义。可以说,公钥密码体制的出现在密 码学发展史上是一次质的飞跃。 5 码学发展史 是 次质的飞跃
对称密码体制的缺陷 通信双方要进行加密通信,需要通 过秘密的安全信道协商加密密钥, 。密钥分配问题 而这种安全信道在实际中很难实现。 在有n个用户的通信网络中,每个用户要想和其它n-1 个用户进行通信,必须使用-1个密钥,而系统中的 。密钥管理问题 总密钥量将达到n(n-1)/2。当n较大时,这样大的密钥 量,在产生、保存、传递、使用和销毁等各个环节中 都会变得很复杂,存在着安全隐患。 。数字签名问题 对称密码体制中通信双方拥有同样的密钥, 所以接收方可以伪造签名,发送方也可以 否认发送过某消息,难于解决陌生人之间 的身份认证和交易信息认证的问题。 6 CNR@HEU http://machunguang.hrbeu.edu.cn
对称密码体制的缺陷 通信双方要进行加密通信,需要通 过秘密的安全信道协商加密密钥 密钥分配问题 过秘密的安全信道协商加密密钥, 而这种安全信道在实际中很难实现。 密钥管 问 在有 n个用户的通信网络中,每个用户要想和其它 n -1 个用户进行通信,必须使用 n -1个密钥,而系统中的 密钥管 理 问 题 总密钥量将达到 总密钥量将达到 n ( n -1)/2 。 当 n较大时,这样大的密钥 量,在产生、保存、传递、使用和销毁等各个环节中 都会变得很复杂,存在着安全隐患 。 数字签名问题 对称密码体制中通信 方拥有同样的密钥 对称密码体制中通信 双方拥有同样的密钥, 所以接收方可以伪造签名,发送方也可以 否认发送过某消息,难于解决陌生人之间 6 的身份认证和交易信息认证的问题
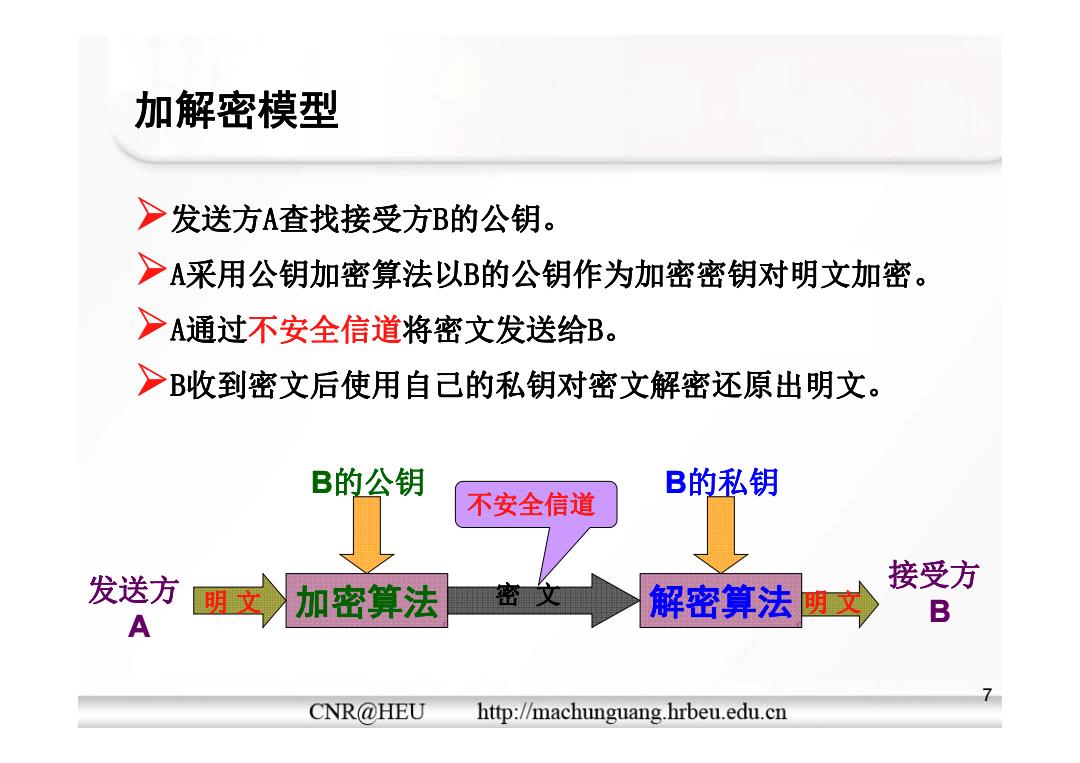
加解密模型 >发送方A查找接受方B的公钥。 >A采用公钥加密算法以B的公钥作为加密密钥对明文加密。 >A通过不安全信道将密文发送给B。 >B收到密文后使用自己的私钥对密文解密还原出明文。 B的公钥 B的私钥 不安全信道 发送方 密文 接受方 明 加密算法 解密算法 明文 A B CNR@HEU http://machunguang.hrbeu.edu.cn
加解密模型 ¾发送方A查找接受方B的公钥。 ¾A采用公钥加密算法以 采用公钥加密算法以B的公钥作为加密密钥对明文加密。 的公钥作为加密密钥对明文加密。 ¾A通过不安全信道将密文发送给B。 ¾B收到密文后使用自己的私钥对密文解密还原出明文。 B的公钥 B的私钥 不安全信道 发送方 明 文 加密算法 密 文 解密算法 明 文 A 接受方B 7

基本原理(陷门单向函数) >正向计算容易。即如果知道密钥P和消息M,容易计 算C=f(M >在不知道密钥S的情况下,反向计算不可行。即如果只 知道加密后的消息C而不知道密钥S.,则计算不可 行M=(C >在知道密钥S的情况下,反向计算容易。 即如果同时知 道加密消息C和密钥S,则计算M=s(G是容易的。这 里的密钥S相当于陷门,它和P配对使用。 8 CNR@HEU http://machunguang.hrbeu.edu.cn
基本原理(陷门单向函数) ¾正向计算容易 即如果知道密钥 和消息M 容易计 ( ) ¾正向计算容易。即如果知道密钥 P 和消息M,容易计 算 。 ( ) k CfM = p Pk ¾在不知道密钥 的情况下,反向计算不可行。即如果只 的情况下,反向计算不可行。即如果只 知道加密后的消息C而不知道密钥 ,则计算不可 Sk 知道加密后的消息C而不知道密钥 S ,则计算不可 行 。 ¾ k S 1 M f C( ) − = ¾在知道密钥 的情况下,反向计算容易。即如果同时知 的情况下,反向计算容易。即如果同时知 道加密消息C和密钥 ,则计算 是容易的。这 Sk S ( ) 1 M f S C − 道加密消息C和密钥 ,则计算 = 是容易的。这 里的密钥 相当于陷门,它和 相当于陷门,它和 配对使用。 Sk Sk M f (C) Sk Pk 8

公钥密码算法应满足的要求 >接收方B产生密钥对(公钥PK和私钥SK?)在计算上是容易 的。 >发送方A用接收方的公钥对消息m加密以产生密文c,即 c=Et,(m)在计算上是容易的。 >接收方B用自己的私钥对c解密,即m=Dk,(C)在计算上是容 易的。 >攻击方由B的公钥PK求私钥SK在计算上是不可行的。 >攻击方由密文c和B的公钥PK恢复明文m或求私钥SKg (选择 明文攻击)在计算上是不可行的。 9 CNR@HEU http://machunguang.hrbeu.edu.cn
公钥密码算法应满足的要求 ¾接收方 B产生密钥对 (公钥PK B和私钥SK B )在计算上是容易 在计算上是容易 的。 ¾发送方A用接收方的公钥对消息 用接收方的公钥对消息m加密以产生密文 加密以产生密文c,即 cE m = pk ( ) 在计算上是容易的 在计算上是容易的 。 ¾接收方B用自己的私钥对 用自己的私钥对c解密,即 在计算上是容 易的 。 ( ) B pk ( ) B mD c = sk 易的 。 ¾攻击方由B的公钥PK B求私钥SK B在计算上是不可行的。 ¾攻击方由密文c和B的公钥PK B恢复明文m或求私钥SKB (选择 明文攻击 )在计算上是不可行的 。 9 明文攻击 )在计算上是不可行的

公钥密码算法思考的主要问题 >私钥和公钥是如何生成的,它们之间有着怎样的关系; 》>安全的密钥长度是多少; >公钥密码体制的安全性依赖的数学难题是什么; >如何实现加密算法(公钥加密),以及解密算法(私钥解密), 反之亦然(数字签名); >现在这种公钥密码体制的安全分析。 10 CNR@HEU http://machunguang.hrbeu.edu.cn
公钥密码算法思考的主要问题 ¾私钥和公钥是如何生成的,它们之间有着怎样的关系; ¾安全的密钥长度是多少; ¾公钥密码体制的安全性依赖的数学难题是什么; ¾如何实现加密算法 如何实现加密算法 (公钥加密 ),以及解密算法 (私钥解密 ), 反之亦然(数字签名); ¾现在这种公钥密码体制的安全分析。 10

常用算法 ●背包问题(NP问题)。 背包算法 ●基于大整数素因子分解问题。 RSA,Rabin等 ●基于有限域乘法群上的离散对数问题。 Elgamal(DS)。 ●椭园曲线上的离散对数问题。 ECC。 ●基于身份的密码体制 IBE。 11 CNR@HEU http://machunguang.hrbeu.edu.cn
常用算法 背包问题(NP问题)。 背包算法 基于大整数素因子分解问题。 RSA,Rabin等 基于有限域乘法群上的离散对数问题。 Elgamal Elgamal(DS)。 椭园曲线上的离散对数问题。 ECC。 基于身份的密码体制 IBE。 11