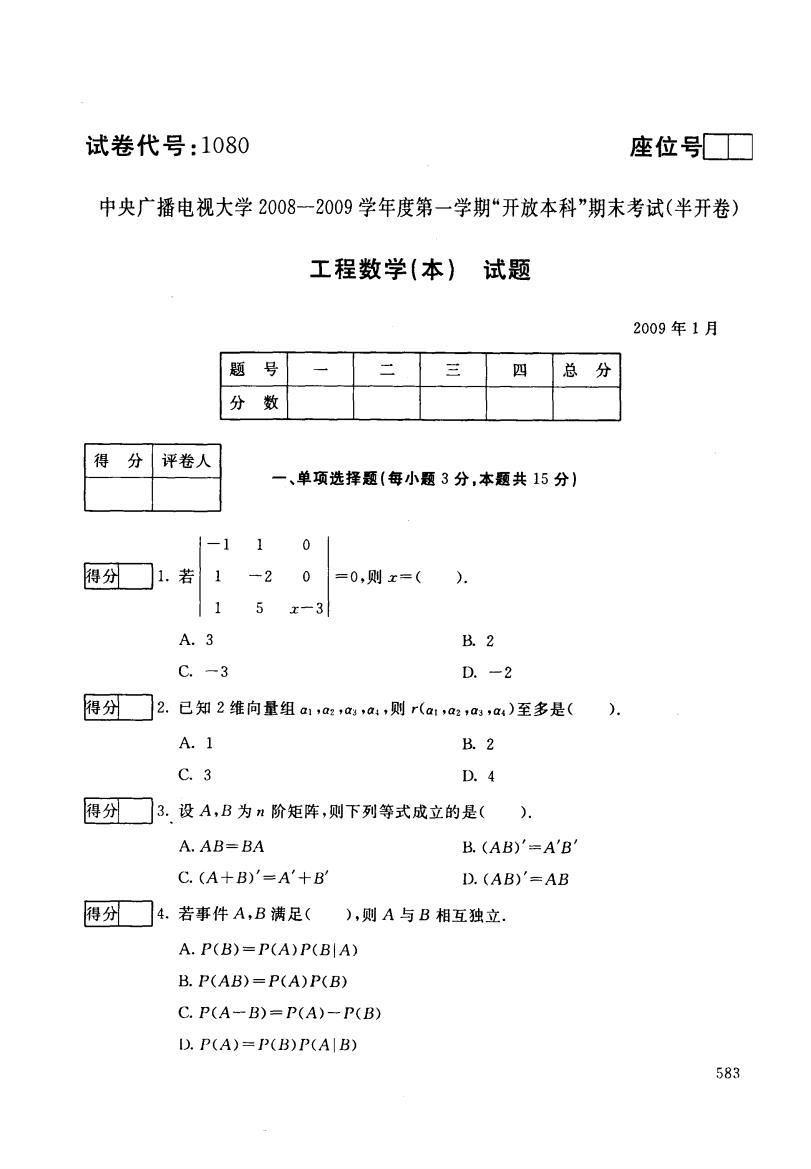
试卷代号:1080 座位号■ 中央广播电视大学2008一2009学年度第一学期“开放本科”期末考试(半开卷) 工程数学(本) 试题 2009年1月 题 冬 三 四 总 分 分 数 得分 评卷人 一、单项选择题(每小题3分,本题共15分) -1 1 0 得分 1. 若 -20 =0,则x=( 1 5 x-3 A.3 B.2 C.-3 D.-2 得分 2. 已知2维向量组a1,a2,a4,a4,则r(a1,a2,a,a4)至多是( A.1 B.2 C.3 D.4 得分 3.设A,B为n阶矩阵,则下列等式成立的是( A.AB=BA B.(AB)'=A'B' C.(A十B)'=A'+B D.(AB)'=AB 得分 4. 若事件A,B满足( ),则A与B相互独立. A.P(B)=P(A)P(BA) B.P(AB)=P(A)P(B) C.P(A-B)=P(A)-P(B) D.P(A)=P(B)P(AB) 583
试卷代号:1080 座位号巨工二 中央广播电视大学2008-2009学年度第一学期“开放本科”期末考试(半开卷) 工程数学(本) 试题 2009年 1月 题 号 四 总 分 分 数 得 分 评卷人 一、单项选择题(每小题3分,本题共 15分) 二1. 71}一 } 1 1 ‘一 2 =0,则 x=( 5 x一 3 A. 3 B. 2 C. 一 3 D. 一 2 F 44 -3亚T 12·已知“维向量组ai ,a2 ,a3a,,则 r(al,a2,a3,aa)至多是( A. 1 C. 3 B. 2 D. 4 3.设 A,B为 n阶矩阵,则下列等式成立的是( B. U A. AB=BA C. (A十B)‘=A' +B (AB)‘=A'B' (AB)’=AB 匡王习4·若事件A, “满足‘ ,则 A 与B相互独立. A.P(B)=P(A)P(B}A) P(AB)=P(A)P(B) C. P(A一B)二P(A)一P(B) l). P (A)“P(B)P(A}B) 583

得分■ 5.若随机变量X的期望和方差分别为E(X)和D(X),则等式( )成立 A.D(X)=E[X-E(X)] B.D(X)=E(X2)+[E(X)] C.D(X)=E(X2) I).D(X)=E(X2)-[E(X)]2 得分 评卷人 二、填空题(每小题3分,本题共15分) 得分6.设A,B均为n阶可逆矩阵,逆矩阵分别为A-1,B1,则(B1A)= 得分☐7.向量组。1=(1,1,0),2=(0,1,1),=(1,0,k)线性相关,则k= 得分☐8.已知P(A)=0.8,P(AB)=0.2,则P(A-B)=一 -10251 得分 已知随机变量X~ ,那么(X)= 0.30.10.10.5J 得分 10. 设1…,是来自正态总体N(,4)的一个样木,则0》 10 得分 评卷人 三、计算题(每小题16分,本题共64分)】 r -127 得分 11.设矩阵A= 2-35 ,求(1)|A1,(2)A. L3 -24 x1-x2十x4=2 得分 12.当入取何值时,线性方程组 x1-2x2+x,十4x4=3 有解,在有解的情况 2x1-3x+x3十5x1=λ+2 下求方程组的全部解. 得分13.设X~N(3,4),试求(1)P(57).(已知中(1)=0.8413,Φ(2) =0.9772,(3)=0.9987) 584
I "I口5.若随机变量、的期望和方差分别为:(X)和。(、),则等式( )成立. A. D(X)=E[X一E(X)] C. D(X)=E(X2) 13. D(X)“E(X2)+[E(X)]2 U. D(X)=E(X2)一〔E( X)]2 得 分 评卷人 二、填空题(每小题 3分,本题共 15分) 匣王习6·设A, ”均为)7阶可逆矩 阵,逆矩 阵分 别为 A-', B-',则 (B_, A')一’二 .向量组a,= (1,1,0), a2=(0,1,1),a、二(1,0,k)线性相关,则k= 已知 P(A)=0. 8,P(AB)=0. 2,则 P(A-B)= 「一1 0 2 5 ] 已知随机变量X- _ 卜那么E( X)二_ _ . L 0. 3 0. 1 0. 1 0. 5」 勺了 0 曰 0 口 10·设xi , x2 -, xio是来自正态总体N(te,4)的一个样刁、,则壳Z 1o 画画画 画 三、计算题(每小题 16分,本题共 64分) F1 一 1 2} 「二- 万门- 一 一1 、_ , _. 】 I 1 t,一 111.设矩1;V A一{ L 2 3 一一 3 2 5 41 1I’求(”IAI,(2)A’· 画12. ·/取何·时, 一 XI一x:十x4=2 x, -2x2十x,件一4x4 = 3 有解,在有解的情况 2x,一3x:一卜x,+5X4二A+2 下求方程组的全部解. 匣王习13·设X-N(3,4),试求(1)P(57).(已知。(1)=0.8413,(P(2) =0. 9772.中(3)= 0.9987) 384

得分 14.已知某种零件重量X~N(15,0.09),采用新技术后,取了9个样品,测得重量 (单位:kg)的平均值为14.9,已知方差不变,问平均重量是否仍为15(检验显著 水平a=0.05,o.75=1.96)? 得分 评卷人 四、证明题(本题6分)】 得分15.设A,B是两个随机事件,试证:P(B)=P(A)P(BA)十P(A)P(BA) 585
匣亚口14.已知某种零件重量X^-N(15,0.09),采用新技术后,取了9个样品,测得重量 (单位:kg)的平均值为 14.9,已知方差不变,问平均重量是否仍为 15(检验显著 水平 a=0. 05,uo.9,,=1.96)? 得 分 评卷人 四、证明题 (本题 6分) 匣王口15.设A,。是两个随机事件,试证:P(B) =P(A)P(B I A)+P(A)P(B I A). 585

试卷代号:1080 中央广播电视大学2008一2009学年度第一学期“开放本科”期末考试(半开卷) 工程数学(本) 试题答案及评分标准 (供参考) 2009年1月 一、单项选择题(每小题3分,本题共15分) 1.A 2.B 3.C 4.B 5.D 二、填空题(每小题3分,本题共15分) 6.(A-1)'B 7.-1 8.0.6 9.2.4 10.N,) 三、计算题(每小题16分,本题共64分)】 -12 -1 2 1 -1 11.解:(1)1A|=12-35= 10 -1 1 …6分 3 -240 1 -2 0 (2)利印冯等行变换得 -21007 -1 2 1007 2 ;501 0 *10 1 1 -210 -24001」 -2 -301 1-12 1 007 1 -1210 0 +0一1 1 -210+0 1 -12-1 0 00 -1 -511 Lo 0 1 5 -1 1 r1-10-9 2 21 100 -2 0 0 7 -2 -1 +010 7 -2 一1 0 0 15 -1 N 001 5-1-1 586
试卷代号:1080 中央广播电视大学2008-2009学年度第一学期“开放本科”期末考试(半开卷) 工程数学(本) 试题答案及评分标准 (供参考) 一、单项选择题(每小题 3分,本题共 15分) 1. A 2.B 3. C 4. B 5. D 二、填空题(每小题 3分.本题共 15分) (A一‘)'B 一 1 8. 0. 6 9. 2.4 4 、 1u. 1v lu,- ) lu 三、计算题(每小题 16分,本题共 64分) {‘一‘ 11.解:(1) IA{二}2 一3 1 一 1 0 一 1 1 一 1 2 2009年 1月 6分 3 一 2 4 一 2 一 1 (2)利尸 " !j等行变换得 刁 ! ! 1 口 0 八U 工. 上 一 1 一 l 1 一 3 0 2 1 一 1 2 ︵. 1 Q 山 we ,.工 C ︺ 一 - ︿U 以 | |阳 1卜 山 t ﹁1 十 ︼ 0 0 ..1 2 1 0 5 0 2 4 0 0 曰曰|.防 甘 1匕曰 口 | 伙 四 | 比 t ﹁1苦ee |! 1 n 口 门 ︸ ,几 书 ︵U l几 ︷ 1 1 9 目 巴 J C乙 一 - 一 1 2 一 1 1 0 一 1 一 1 0 一 9 一 1 0 一2 0 一 1 一 1 一 0 7 一 2 一 1 一 1 一 1 一0 7 一 2 一 1 586 一 1 一 1」

「-2 0 即 A-1- -2 ……16分 5 -11 12.解:将方程组的增广矩阵化为阶梯形 1-101 21 ◇ -1012 1-214 3 0 -113 1 2-315λ+2 10 -113λ-2 1-101 2 10-1-21 +0-113 0 1-1 -3 一1 000λ-3」 000 0 λ-3 由此可知当入≠3时,方程组无解.当入=3时,方程组有解.……8分 此时相应的齐次方程组的一般解为 x1=xg十2x4 (x3、x4是自由未知量) x2=x3+3x 分别令x=1,x4=0及x=0,x4=1,得齐次方程组的一个基础解系 X1=[1110]',X2=[2301]1 令x:=0,x=0,得非齐次方程组的一个特解 X。=[1-100]/ 由此得原方程组的全部解为 X=X。十k1X1十k2X2(其中k,,k2为任意常数) 16分 1.解:1P57=PX23723) 2 =n(X23>2)=1-PX23<2) =1-Φ(2)=1一0.9772=0.0228 16分 587
﹁ i l es es es e e we l es es es es es J 1 八乙 二 ︸.1 0 一 一 9 一 白 7 5 厂 ! l we .es we l .L 即 A 12.解 :将方一程组的增广矩阵化为阶梯形 Q 乙 1 上 1 孟 g d n 甘 ,上 一 - 0 1 2 又+ 2 一 1 1 3 A一2 盛任 ︻勺 一 胜! I J 11 cj 1 1 - 1 八 - 0 一 1 一 2 1 2 3 一 - - 一 一 1 一 1 一 3 0 0 0 A一 3 0 0 0 由此可知当 A z7-` 3时 ,方程组无解.当A=3时,方程组有解. 此时相应的齐次方程组的一般解为 =x,十2x4 (Xs ,x4是 自由未知量) x, +3x4 X X r! j 、 分别令 x3=1,x4=0及 x,=0,x4=1,得齐次方程组的一个基础解 系 X,=仁1 1 1 0]',Xz=[2 3 0 1]' 令 xs=0,x4=0,得非齐次方程组的一个特解 Xo=[1 一1 0 0]' 由此得原方程组 的全部解为 X=Xo+k,X,十k2 XI (其中k, ,k2为任意常数)·····························。······…… 13. ,解 :(,,1、)Pn,(尸57)=P ) 2 ‘ 2 =P 一(竺X长一书3二 一> 2、)二 ,1一P一(/X-共一-3<__2、) 2 -一‘ 一 ‘“ 2 “一 “ 1一 中(2)= 1一 0.9772= 0. 0228 16分 8分 16分 8分 16分 587

14.解:零假设1。:u=15.由于已知σ=0.09,故选取样本函数 U=x是~N(0,1) …………5分 a/n 已知x=14.9,经计算得 g=0.3=0.1, 3 =} 11分 由已知条件4.95=1.96, x二4 aNn =1<1.96=4a.975 故接受零假设,即零件平均重量仍为15…………………16分 四、证明题(本题6分) 15.证明:由事件的关系可知 B=BU-B(A+A)=AB+AB 而(AB)(AB)=O,故由加法公式和乘法公式可知 P(B)=P(AB)+P(AB)=P(A)P(BIA)+P(A)P(BIA) 证毕。 ………6分 588
14.解:零假设 fl, o k=15.由于已知了=0. 09,故选取样本函数 U一Q/ n一“‘ 。 ”’ 已知 二二]4.9,经计算得 夕一。.3一,、,{- p 1/5一3一v. 1’{。/而 14. 9一 15 0. 1 由已知条件 U0.975 - 1. 96 , {X-u{一1_,。,_ {o/ n{一‘<1. 96一。〔,.。:。 故接受零假设,即零件平均重量仍为 15.···················..;,一···········............…… 5分 11分 16分 四、证明题(本题 6分) 15.证明:由事件的关系可知 B二BU-B(A一十兀)=AB十刃, 而(AB) (AB)二②,故由加法公式和乘法公式可知 P(B)=尸(AB)斗一P(几3)=P(A)P(B}A)+P(兀)1) (B}两) 证毕.·····························································································…… 6分 58吕