金属强韧化 固溶原子 与位错的弹性、静电、化 学等交互作用 固溶强化 位错 。?? 位错强化 晶界 细晶强化 第二相颗粒 颗粒强化
• 与位错的弹性、静电、化 固溶原子 学等交互作用 位错 • ?? 晶界 第二相颗粒 固溶强化 位错强化 细晶强化 颗粒强化 金属强韧化
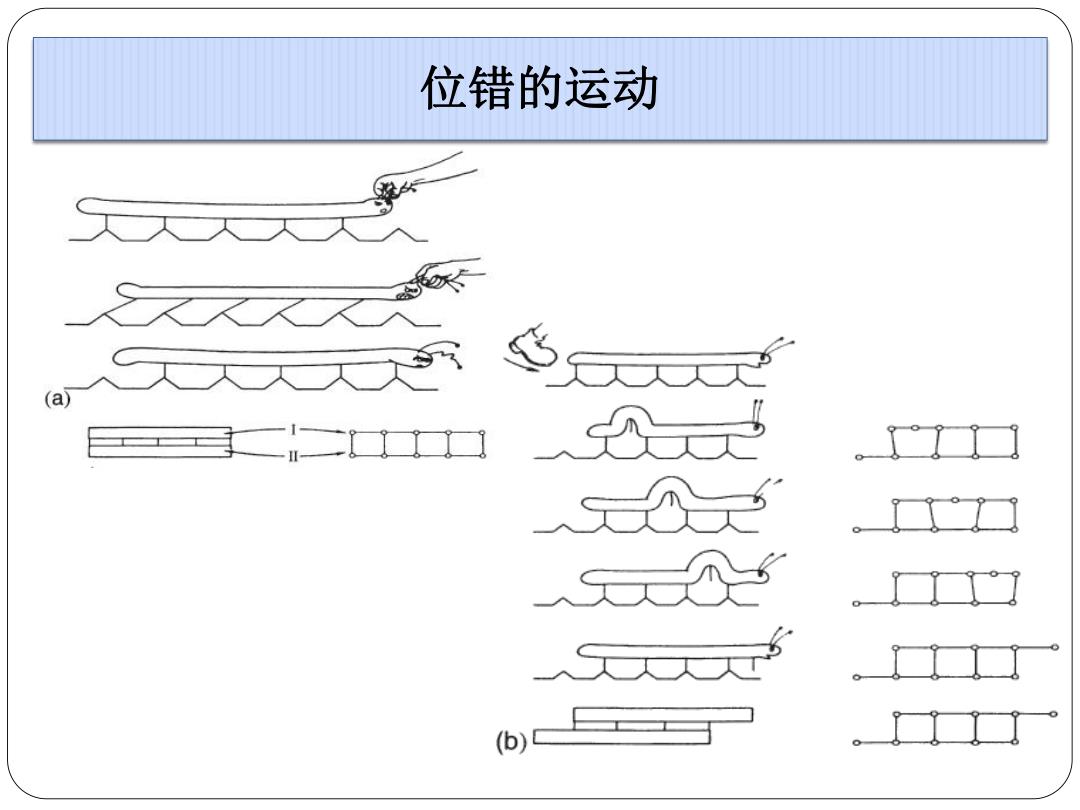
位错的运动 (a) 垂 (b)
位错的运动

Orowan's equation y=bov h Y=(AL/L).b/h T=b/h Take a piece of crystal with volume:V=Lhl If one dislocation glides through the whole crystal the added shear strain is:y=b/h If one dislocation glides through part of the crystal the added shear strain is: △Lb Lh If N dislocations glide through part of the crystal the added shear strain is: Y=N △LbWN△LbNI△Lb Lh I Lh V NI .Dislocation density [m/mis defined by:P ÷Y=pALb And strain rate by:= oyb)p) 8t
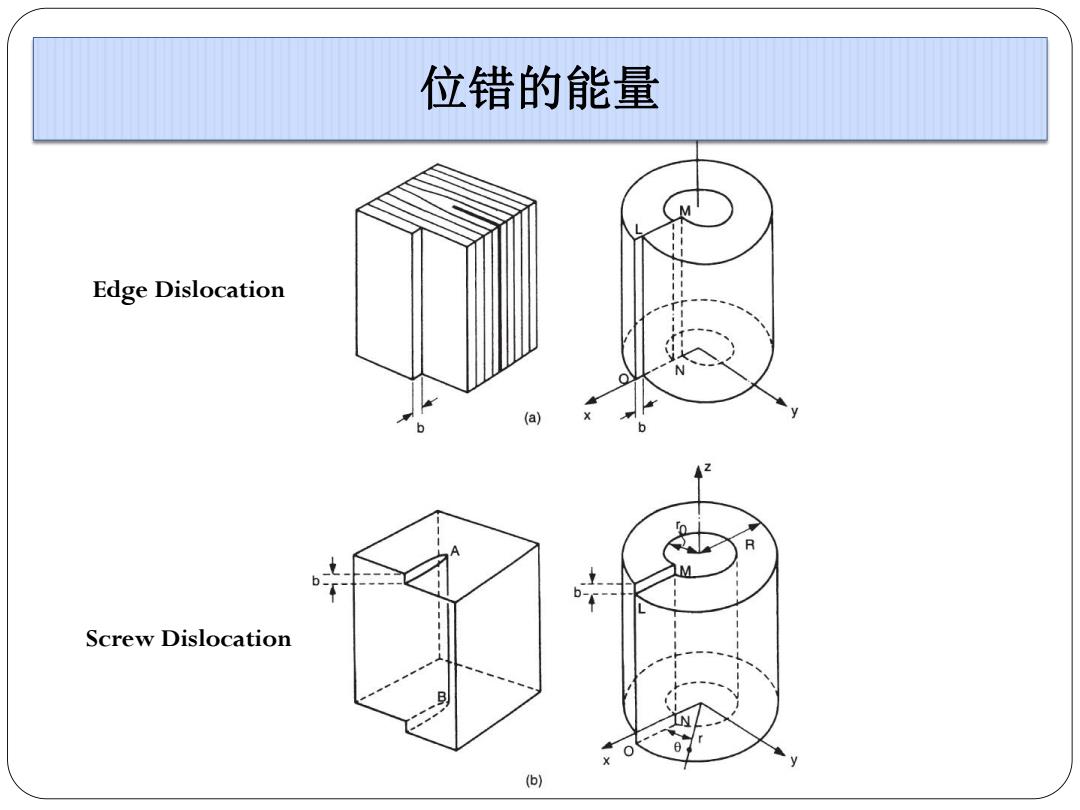
位错的能量 M Edge Dislocation (a) R Screw Dislocation (b)
位错的能量 Edge Dislocation Screw Dislocation
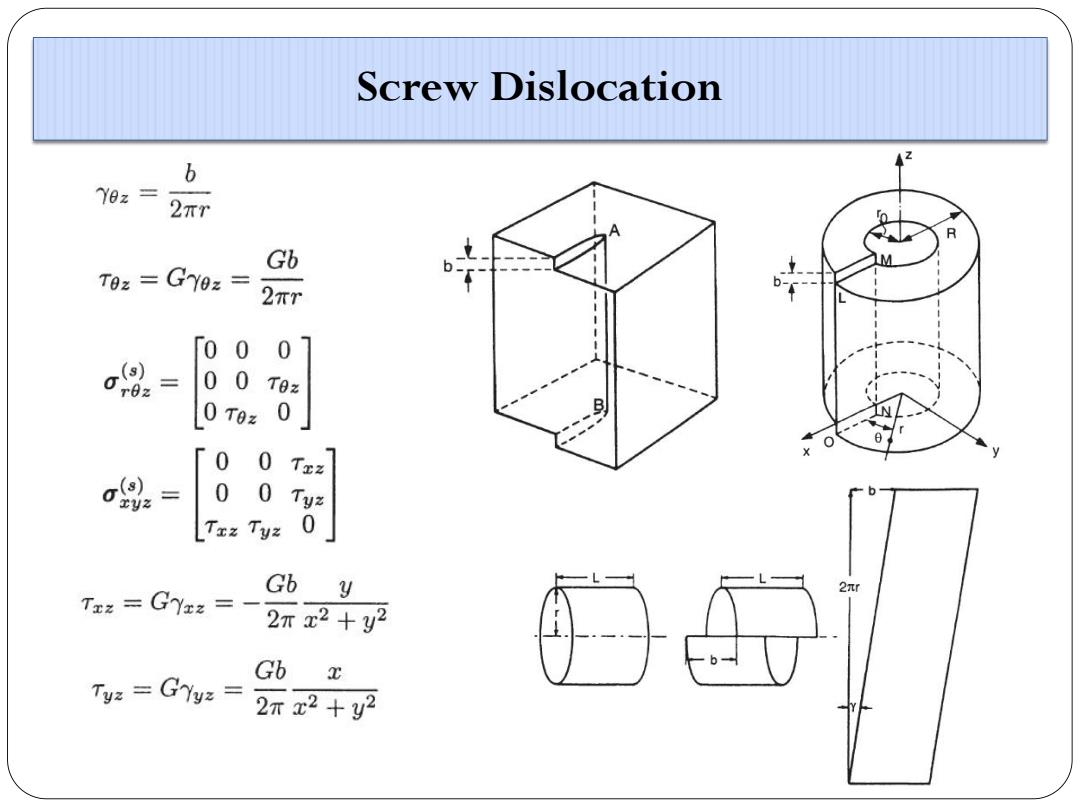
Screw Dislocation b Y0z= 2πr Gb T8z=( 2r7 To 0 0 0 0 0 TOz LO TOz 0 [0 0 Toz 岛 0 0 Tyz Txz 0 Gb 2nr Taz =GYa:=- y 2T z2 +y2 Ty:GTy:= Gb z 2元x2+y2
Screw Dislocation
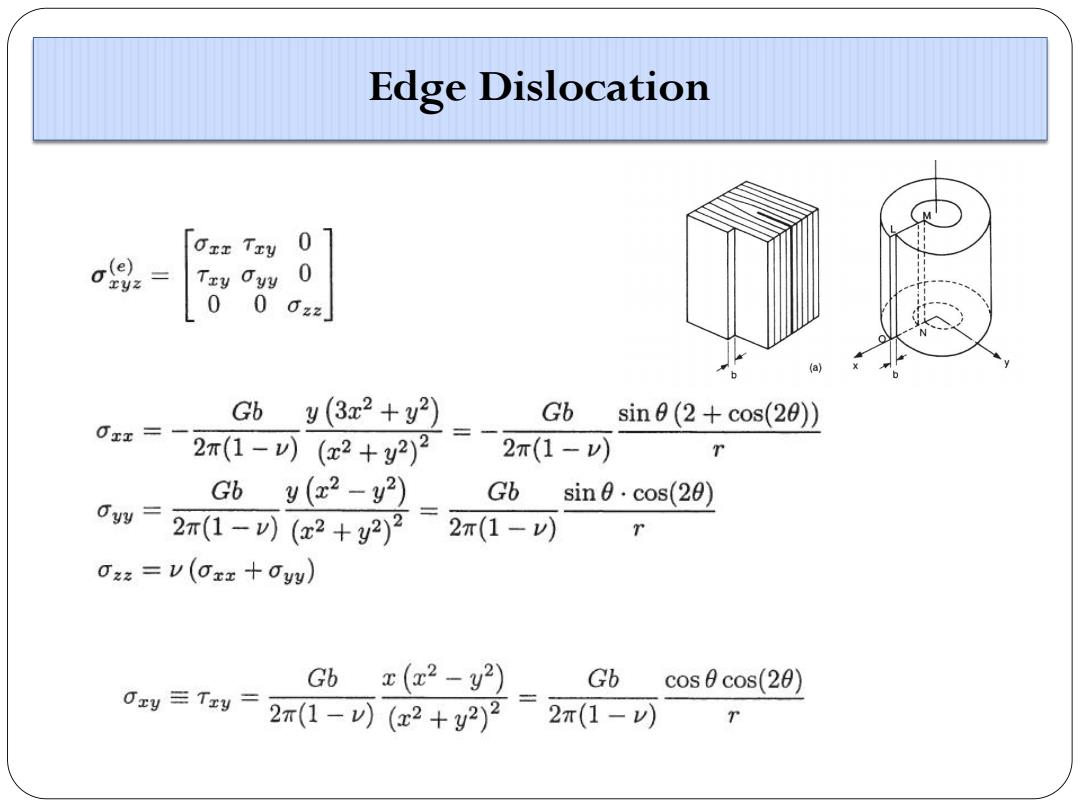
Edge Dislocation 0x工 Try 0 9 y Oyy 0 0 00z2 a 0x Gb y(3x2+y2) Gb sin0(2+cos(20)) 2T(1-0(x2+y2)2 2π(1-V)) Ow= Gb y(22-y2) Gb sin 0.cos(20) 2x(1-0)(x2+92)2 2m(1-V) O2:=v(Oxz +Oyy) Gb x(x2-y2) Gb cosθcos(28) 0y=Txy=2r(1-(2+y2)2 -2r(1-)
Edge Dislocation Edge Dislocation
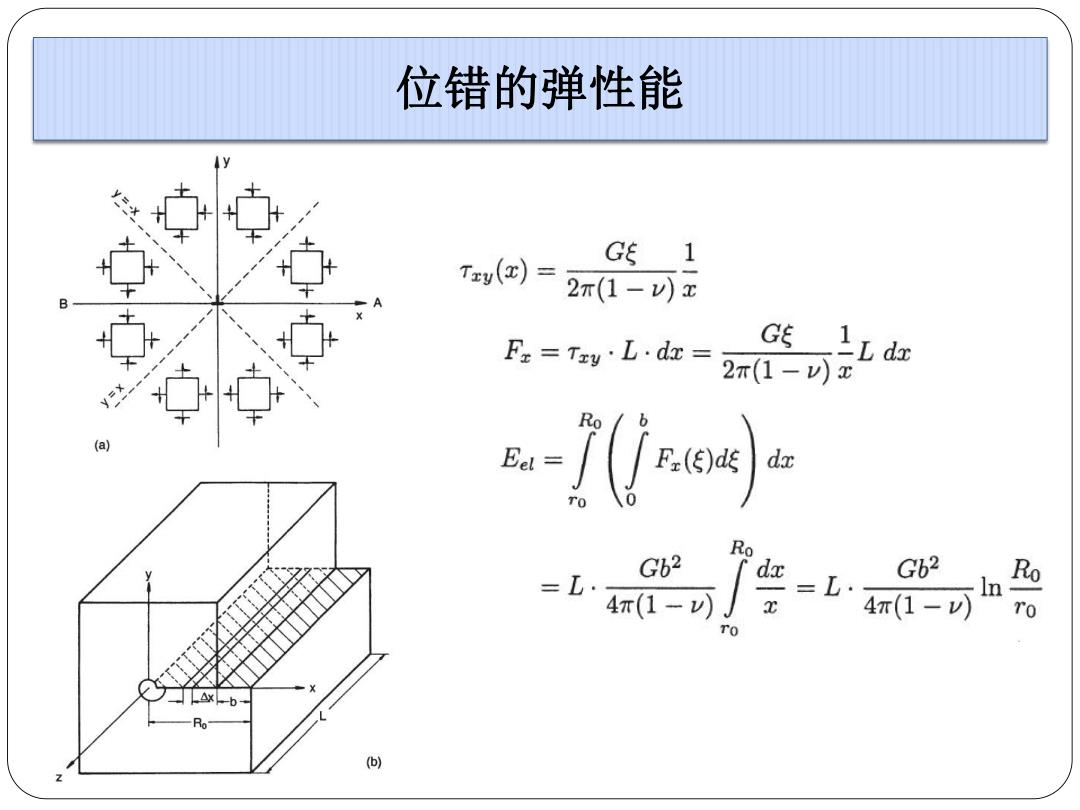
位错的弹性能 T()= G 1 2r(1-)x Fr =Tsy'L.da= G 2r(1-)x (a) da ro Ro Gb2 dx 10 Ro ro △x-b ()
位错的弹性能

位错的总性能 For an assessment of the radial size of the dislocation core ro,one can utilize the fact that the elastic stresses can never exceed the theoretical shear stress Cb T(ro)= 兰Th兰 2 T0≈b Ecore 2 m- Gb2 Gb2 2G 2元 8元 兰 4π(1-) The total energy per unit length of an edge dislocation is 9-号+受=(%+ a screw dislocation E(d兰 1 E(= 器(+1)
For an assessment of the radial size of the dislocation core ro,one can utilize the fact that the elastic stresses can never exceed the theoretical shear stress 位错的总性能

位错的相互作用 F12=(o1b2)×s2 If dislocation 1 intersects the origin of the coordinate system and extends parallel to the z direction,then s=[001]and bi =b2 =6[100]we obtain F12 周--- -0zzb 0 Gb2 cos0 cos(20) 2π(1-)) T
位错的相互作用
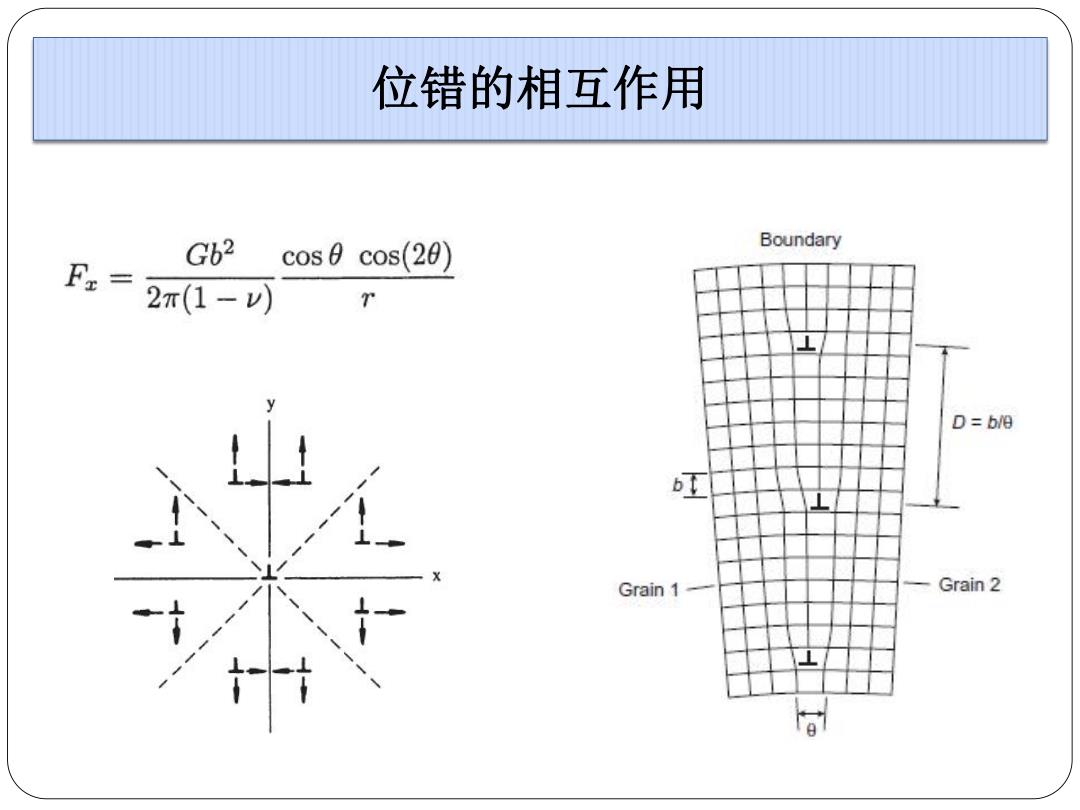
位错的相互作用 Gb2 cos0 cos(20) Boundary 2r(1-V) D=b/8 Grain 1- Grain 2 g
位错的相互作用