
十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育“十一五”国家级规划教材 工程制图 少东开王大家 第4章 立体 4.1立体的投影 4.2平面与立体相交 4.3立体与立体相交
第4章 立体 4.1 立体的投影 4.2 平面与立体相交 4.3 立体与立体相交
”十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育”十一五”国家级规划教材 工程制图 少本X工大军 4.3立体与立体相交 两立体相交表面会产生交线,称为相贯线。 相贯线是两立体表面的共有线
4.3 立体与立体相交 两立体相交表面会产生交线,称为相贯线。 相贯线是两立体表面的共有线
”十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育“十一五”国家级规划教材 工程制图 少本用王大家 平面立体与平面立体相交 P m.5.6 D 分解为求平面与平面立体相交
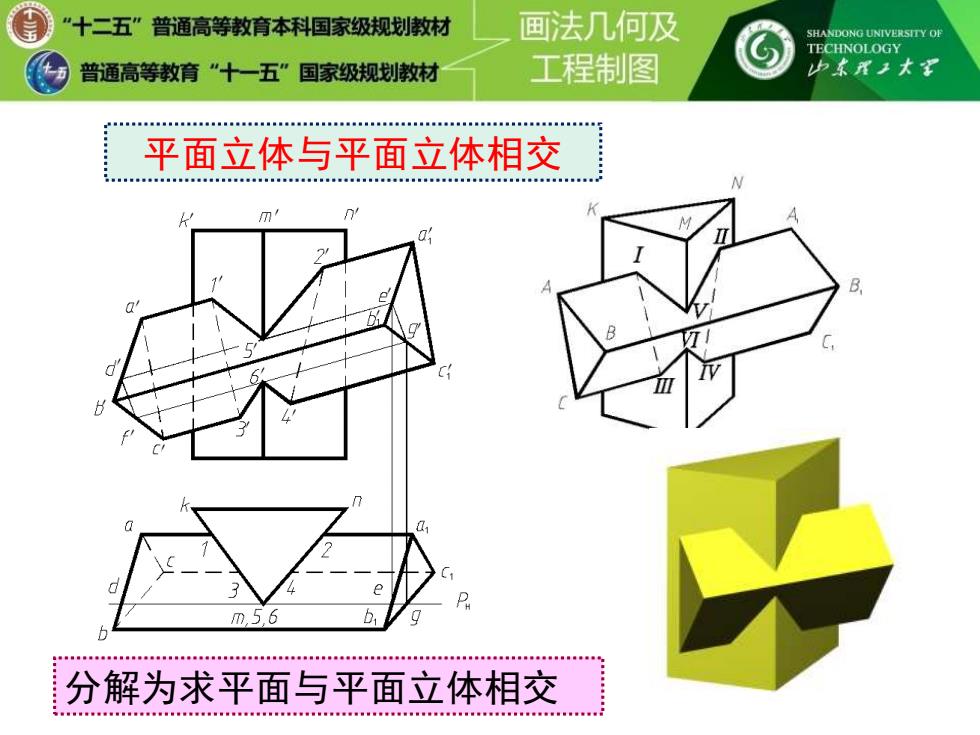
平面立体与平面立体相交 分解为求平面与平面立体相交
”十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育”十一五”国家级规划教材 工程制图 山本用工大军 平面立体与曲面立体相交 a C47 6 0 S. 0 U 分解为求平面与 R 曲面立体相交 EAW4404004144030
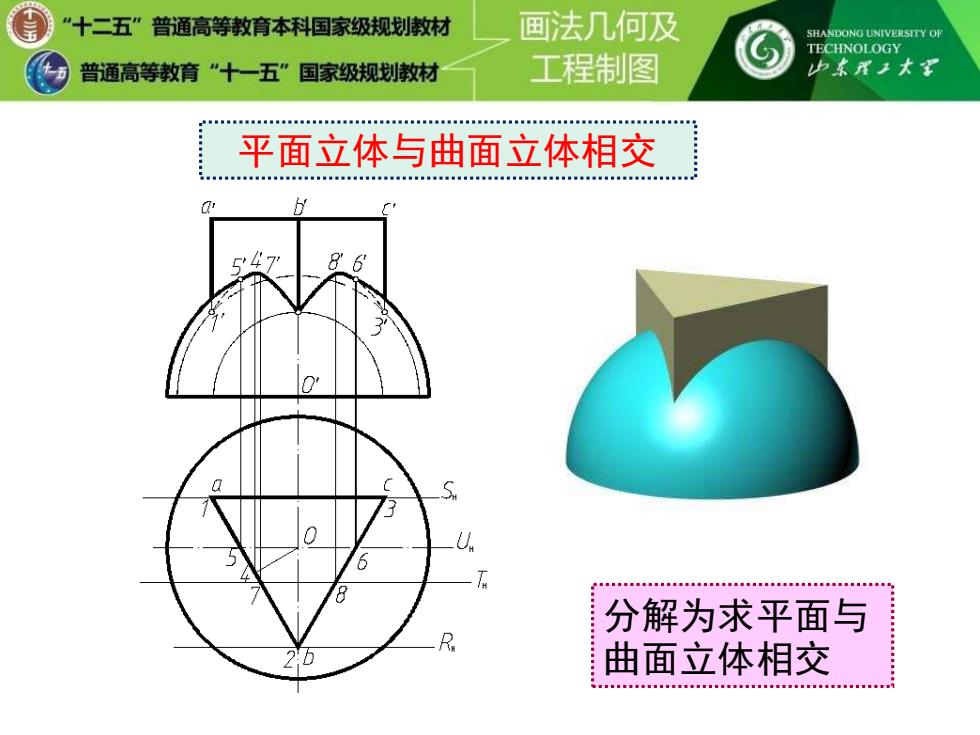
平面立体与曲面立体相交 分解为求平面与 曲面立体相交
”十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育“十一五”国家级规划教材 工程制图 少东开王大家 : 曲面立体与曲面立体相交 11131AA11 两曲面立体相交交线多为空间四次曲线。 特殊情况交线会是平面曲线甚至是直线。 0111.4.44 在不同情况下,求空间曲线的投影的方法有积聚性法、 辅助平面法、辅助球面法等
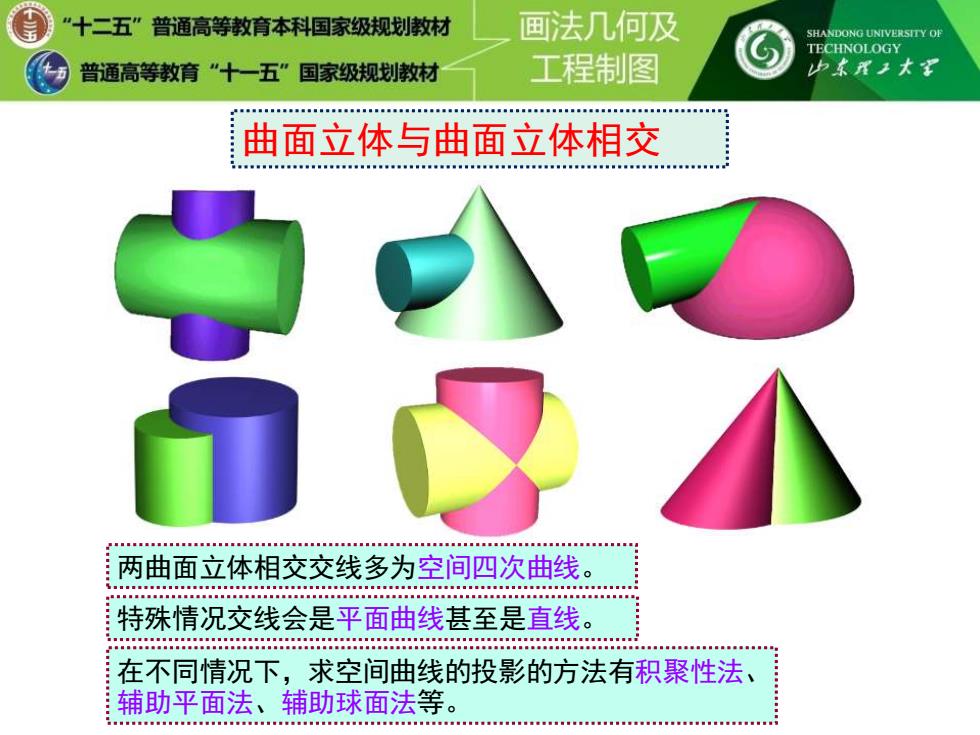
曲面立体与曲面立体相交 两曲面立体相交交线多为空间四次曲线。 在不同情况下,求空间曲线的投影的方法有积聚性法、 辅助平面法、辅助球面法等。 特殊情况交线会是平面曲线甚至是直线
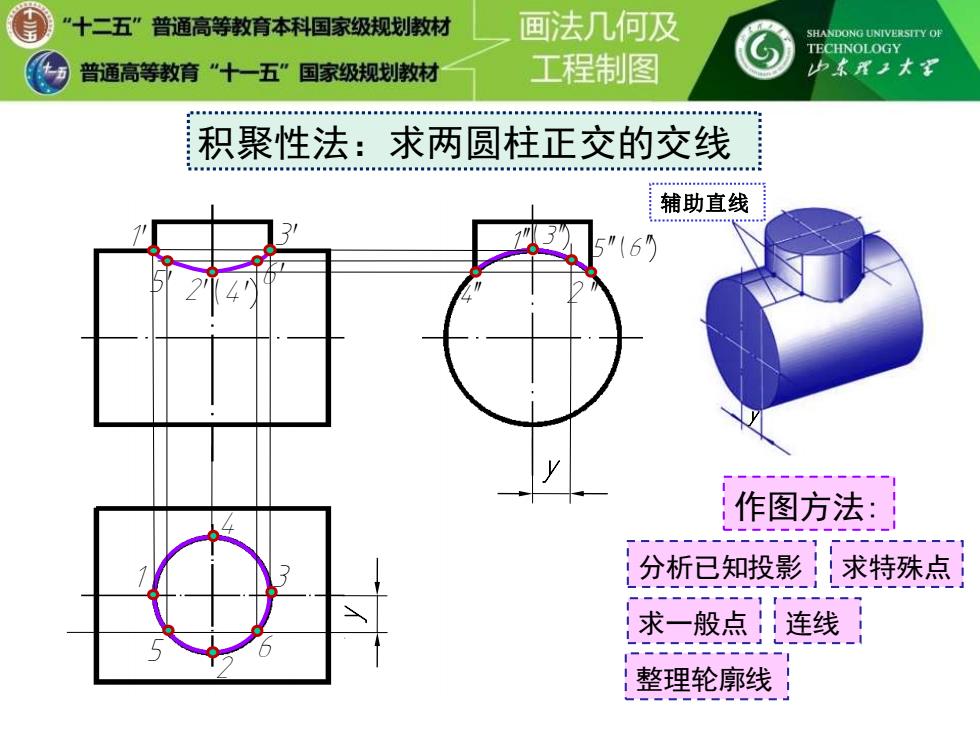
”十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育”十一五”国家级规划教材 工程制图 山N工大到 积聚性法:求两圆柱正交的交线 辅助直线 作图方法: 分析已知投影 求特殊点 求一般点连线 整理轮廓线
积聚性法:求两圆柱正交的交线 1′ 3′ (4′) 4′′ 2 ′′ 2 1 作图方法: 求特殊点 求一般点 连线 整理轮廓线 分析已知投影 y y y 辅助直线 3 4 5 6 5′2′ 6′ 1′′(3′′) 5′′(6′′)

”十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育“十一五”国家级规划教材 工程制图 少东开王大家 两圆柱正交的三种情形 两圆柱正交的三种情形 两实心圆柱相交 。交 实心圆柱与 两圆柱孔相交 圆孔相交
两圆柱正交的三种情形 两实心圆柱相交 实心圆柱与 圆孔相交 两圆柱孔相交

”十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育”十一五”国家级规划教材 工程制图 山本用工大军 两圆柱正交直径不同时 的交线变化 Φd2 中d 两曲线 两曲线 两直线 d≤D d<d<D 0 :
两圆柱正交直径不同时 的交线变化 d1<D d1<d2<D d=D

”十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育“十一五”国家级规划教材 工程制图 少本开王大家 两圆柱正交应用举例
两圆柱正交应用举例
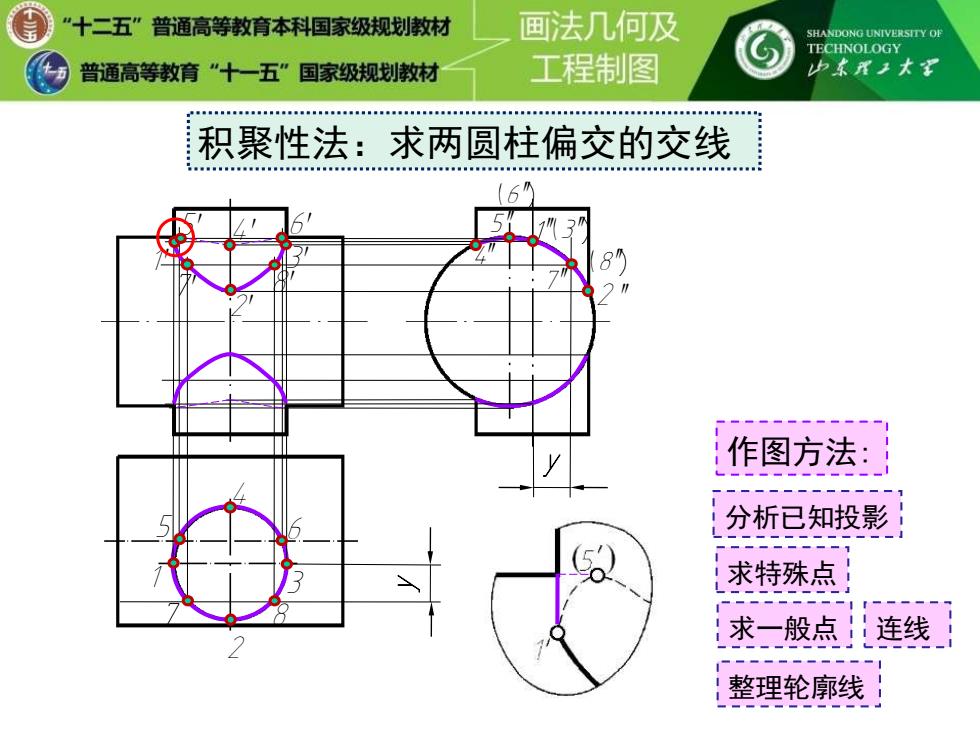
”十二五”普通高等教育本科国家级规划教材 画法几何及 SHANDONG UNIVERSITY OF TECHNOLOGY 普通高等教育”十一五”国家级规划教材 工程制图 山尾王大到 积聚性法:求两圆柱偏交的交线 作图方法: 分析已知投影 求特殊点 求一般点连线 整理轮廓线
积聚性法:求两圆柱偏交的交线 作图方法: 求特殊点 求一般点 连线 整理轮廓线 分析已知投影 y y 1′ 3′ 2 ′′ 4′′ 2 1 3 2′ 5′ 6′ 5′′ 1′′(3′′) 4 6 7 8 (6′′) 7′′(8′′) 4′ 7′ 8′ 5