
数字电子技术第一章逻辑代数 第一章逻辑代数与EDA技术的基础知识 【本章知识架构】 逻辑代数的基本概 基本和常用逻辑运算 念、公式和定理 公式和定理 逻辑函数的标准与或式和 最简式 逻辑代数基 逻辑函数的化简方法 逻辑函数的公式化简法 逻辑函数的卡诺图化简法 础知识 具有约束的逻辑函数的化简 逻辑函数的表示方法 几种表示逻辑函数的方法 及其相互之间的转换 几种表示方法之间的转换 【本章教学目标与要求】 ·理解与、或、非逻辑函数 理解基本和常用逻辑门的工作原理 。 掌握布尔代数描述与门、或门、非门的运算逻辑 在与非门和或非门应用布尔代数 使用布尔代数描述组合逻辑函数 ·说明如何使用积项和或和项积的形式来实现任意的组合逻辑 ·使用卡诺图简化布尔表达式 ·逻辑函数的表示方法及其相互之间的转换 概述 一、概述和逻辑代数 教学目标: 1、了解本课程特点、内容 2、了解本课程学习的要求和目标: 3、理解数字电路的信号特点和电路性质: 4、理解逻辑代数的基本概念 教学重点: 模拟电路和数字电路的特点对比以及信号特点的对比。 教学难点:对数字电路优点的理解
数字电子技术-第一章逻辑代数 1 第一章逻辑代数与 EDA 技术的基础知识 【本章知识架构】 【本章教学目标与要求】 ▪ 理解与、或、非逻辑函数 ▪ 理解基本和常用逻辑门的工作原理 ▪ 掌握布尔代数描述与门、或门、非门的运算逻辑 ▪ 在与非门和或非门应用布尔代数 ▪ 使用布尔代数描述组合逻辑函数 ▪ 说明如何使用积项和或和项积的形式来实现任意的组合逻辑 ▪ 使用卡诺图简化布尔表达式 ▪ 逻辑函数的表示方法及其相互之间的转换 概 述 一、概述和逻辑代数 教学目标: 1、了解本课程特点、内容; 2、了解本课程学习的要求和目标; 3、理解数字电路的信号特点和电路性质; 4、理解逻辑代数的基本概念 教学重点: 模拟电路和数字电路的特点对比以及信号特点的对比。 教学难点:对数字电路优点的理解。 逻 辑 代 数 基 础 知 识 逻辑函数的化简方法 逻辑函数的表示方法 及其相互之间的转换 逻辑代 数的基 本概 念、公式和定理 逻辑函数的标准与或式和 最简式 几种表示逻辑函数的方法 逻辑函数的公式化简法 几种表示方法之间的转换 逻辑函数的卡诺图化简法 基本和常用逻辑运算 公式和定理 具有约束的逻辑函数的化简

数字电子技术.第一章逻辑代数 课程持占,粉字由路是一门专业技术堪础课,应是学习粉字通信枯术,计算机原 理,接口技术,通信系统等专业课程的基础。既有丰富的理论体系, 又具有很强的实 践性。 课程教学内容的联系: 事件要求一逻辑函数一门电路一组合逻辑一时序逻辑一DA转换一事件处理 1.数字信号和数字电路 信号:时间、幅度上都离散。0、1两种状态表示。一一数字信号 时间、幅度上都连续。一 一模拟信号 电路:开关状态。一一数字电路 放大状态。 一一模拟电路 2.数字电路的分类 区分标准:电路结构(分立元件、集成电路) 集成密度(小、中、大等规模) 半导体导电类型(双极型、单极型)」 3.数字电路的优点: 令高度集成: 令可靠性高,抗干扰能力强 令数字信息便于长期保存: 系列多 通用性强,成本低 令保密性好 4.脉冲波形的主要参数 ◇脉冲短 令脉冲上升时间 脉冲下降时间 令脉冲宽度 女脉冲周期与频率 令占空比、 5.逻辑代数 ◇逻辑:事物因果关系的规律 令逻辑函数:自变量和逻辑结果的关系 令逻辑变量:0、1两种取值,代表两种对立的逻辑状态。 二、二进制数表示方法 教学目标: 1、理解各种数制的基本概念
数字电子技术-第一章逻辑代数 2 课程特点:数字电路是一门专业技术基础课,它是学习数字通信技术,计算机原 理,接口技术,通信系统等专业课程的基础。既有丰富的理论体系,又具有很强的实 践性。 课程教学内容的联系: 事件要求-逻辑函数-门电路-组合逻辑-时序逻辑-D/A 转换-事件处理 1.数字信号和数字电路 信号:时间、幅度上都离散。0、1 两种状态表示。——数字信号 时间、幅度上都连续。——模拟信号 电路:开关状态。——数字电路 放大状态。——模拟电路 2.数字电路的分类 区分标准:电路结构(分立元件、集成电路) 集成密度(小、中、大等规模) 半导体导电类型(双极型、单极型)。 3.数字电路的优点: 高度集成; 可靠性高,抗干扰能力强; 数字信息便于长期保存; 系列多,通用性强,成本低; 保密性好。 4.脉冲波形的主要参数 脉冲幅度 脉冲上升时间 脉冲下降时间 脉冲宽度 脉冲周期与频率 占空比、 5.逻辑代数 逻辑:事物因果关系的规律 逻辑函数:自变量和逻辑结果的关系 逻辑变量:0、1 两种取值,代表两种对立的逻辑状态。 二、二进制数表示方法 教学目标: 1、理解各种数制的基本概念

数字电子技术第一章逻辑代数 2、掌握数制转换的方法。 教学重点:数制的概念。 教学难点:转换法则。 数制 概念:数制 一表达数值的方式。 特点:基本特征数决定进制类型。 分类:几种进制介绍 表达:加权和(多项式与和式)表达数值大小。 1、十进制数 由0,1,2,3,4,5,6,7,8,9表示。“逢十进一”;位权:10 例如:234。=2x102+3x10+4x10 (3.14)o=3×10°+1×10+4×10- 在数字电子电路中采用十进制十分不方便,引入二进制。 2、二进制数 用0和1表示:“逢二进一”。位权:2 例(101.11)2=1×22+0×2+1×2°+1×2+1×2 3、十六进制(十六进制在数字电路中,尤其在计算机中得到广泛的应用) 采用0,L,2,3,4,5,6,7,8,9,A(10、B(11)C(12)、D(13、E(14、F(15)十六个数码表 示。“逢十六进一”。位权:16 例(2A7F)2=2×16+10×16°+7×161+15×162=42.4961 4、八进制数(0ctal)-逢八进 用0,1,2,3,4,5,6,7表示:“逢八进一”。 例如(234)=2×82+3×8+4×8 数制转换 1、二进制、八进制、十六进制转换成十进制一一按位权展开即可 (01010110)B=25+24+22+2=(86)D 2、十进制数转换成二进制数:
数字电子技术-第一章逻辑代数 3 2、掌握数制转换的方法。 教学重点: 数制的概念。 教学难点:转换法则。 数制 概念:数制——表达数值的方式。 特点:基本特征数决定进制类型。 分类:几种进制介绍。 表达:加权和(多项式与和式)表达数值大小。 1、 十进制数 由 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 表示。 “逢十进一”;位权:10i 例如: 2 1 0 10 0 1 2 10 (234) 2 10 3 10 4 10 (3.14) 3 10 1 10 4 10 − − = + + = + + 在数字电子电路中采用十进制十分不方便,引入二进制。 2、二进制数 用 0 和 1 表示;“逢二进一” 。位权:2 i 例 2 1 0 1 2 2 (101.11) 1 2 0 2 1 2 1 2 1 2 − − = + + + + 3、十六进制 (十六进制在数字电路中,尤其在计算机中得到广泛的应用) 采用 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 , A(10)、B(11)、C(12)、D(13)、E(14)、F(15)十六个数码表 示。 “逢十六进一”。位权: 16i 例 1 0 1 2 2 (2A.7F) 2 16 10 16 7 16 15 16 42.4961 − − = + + + = 4、八进制数(Octal)- 逢八进一 用 0, 1, 2, 3, 4, 5, 6, 7 表示; “逢八进一”。 例如 2 1 0 8 (234) 2 8 3 8 4 8 = + + 数制转换 1、二进制、八进制、十六进制转换成十进制 ——按位权展开即可 (01010110)B= 26 + 24 + 22 + 21 = (86)D 2、 十进制数转换成二进制数:

数字电子技术.第一章逻辑代数 十进制数整数部分:除2取余法一一直到商为0为止 小数部分:乘2取整法一一转换到误差允许的范围 例1:(6310=(?2 例2:(261)10=(?2 例3:将(0.706)加转换为二进制数,要求其误差不大于20 3、二进制一一十六进制的相互转换:分组法。 例(山100010101110)B=(78AE)加 (01011110,10业0010)B=(5E.B2H BEEF)H=1011111011101111)B (8FA.C6)H=(100011111010.11000110)B ·讨论: 各进制中,适合表示数字信号的是哪一种? 几种数制之间的关系对照表 十进制数二进制数八进制数十六进制数 0 00000 0 0 00001 00010 2 2 00011 3 3 00100 4 4 5 00101 5 5 6 00110 6 6 7 00111 7 7 8 01000 10 8 9 0100 11 9 10 01014 12 A 01011 13 B 12 01100 01101 15 D 01110 16
数字电子技术-第一章逻辑代数 4 十进制数 整数部分:除 2 取余法——直到商为 0 为止 小数部分:乘 2 取整法——转换到误差允许的范围 例 1:(63)10 =(?)2 例 2:(261)10 =(?)2 例 3:将(0.706)D 转换为二进制数,要求其误差不大于 2 -10。 3、 二进制——十六进制的相互转换:分组法。 例 (111 1000 1010 1110)B =(78AE)H (0101 1110 . 1011 0010)B =(5E.B2)H (BEEF)H =(1011 1110 1110 1111)B (8FA.C6)H =(1000 1111 1010 . 1100 0110)B ⚫ 讨论: 各进制中,适合表示数字信号的是哪一种? 几种数制之间的关系对照表 十进制数 二进制数 八进制数 十六进制数 0 1 2 3 4 5 6 7 8 9 10 00000 00001 00010 00011 00100 00101 00110 00111 01000 01001 01010 0 1 2 3 4 5 6 7 10 11 12 0 1 2 3 4 5 6 7 8 9 A 11 12 13 14 01011 01100 01101 01110 13 14 15 16 B C D E

数字电子技术-第一章逻辑代费 15 01111 17 三、二进制代码(码制) 教学目标: 1.理解编码的特点。 2.了解编码的作用。 教学重点:编码的特点及应用。 教学难点:编码的基本概念。编码的转换。 1、编码:用二进制数表示文字、符号等信息的过程。 2、分类 二进制代码:有权码、无权码 二一十进制代码:8421BCD码,余3码等。 可靠性代码: 奇偶校验码,Gray码。 3、常见编码: ①8421BCD码(又称二~十进制码), 即十进制符号和二进制数所对应的十进制数恰好相等。 ②2421码 ©余3码(余3码为无权码,它是8421码加0011得来的) 转换:可以查表 十进几种常见的BCD代码 制数 8421码余3码2421(A码 0 000000110000 0001 0100 0001 00100101 0010 00110110 0011 0100 0111 0100 0101 1000 1011 01101001 1100 01111010 1101 10001011 1110 001110011 权8421 4、格雷码(循环码) 5、ASCⅡ码(其编码见P174表3.3.10)
数字电子技术-第一章逻辑代数 5 15 01111 17 F 三、二进制代码(码制) 教学目标: 1.理解编码的特点。 2. 了解编码的作用。 教学重点:编码的特点及应用。 教学难点:编码的基本概念。编码的转换。 1、编码:用二进制数表示文字、符号等信息的过程。 2、分类: 二进制代码:有权码、无权码 二-十进制代码: 8421BCD 码,余 3 码等。 可靠性代码: 奇偶校验码,Gray 码。 3、常见编码: ○1 8421 BCD 码(又称二~十进制码), 即十进制符号和二进制数所对应的十进制数恰好相等。 ○2 2421 码 ○3 余 3 码(余 3 码为无权码,它是 8421 码加 0011 得来的) 转换:可以查表 4、格 雷 码(循环码) 5、ASCII 码(其编码见 P174 表 3.3.10 )

数字电子技术.第一章逻辑代数 总之:数是用于计算的,而码是人为规定的 (25)10=(11001)2=(19)16 (25)10=(00100101)BcD (01011001)BcD=(59)10 (01011001)2=(89)10 四、EDA技术(后续详细介绍) 一种以计算机作为工作平台,以EDA软件工具为开发环境,以VHDL为设计语 言,以可编程逻辑器件为实验载体,以ASIC、SoC芯片为目标器件,以数字系统设计 为应用方向的电子产品自动化设计技术。 VDL是一种硬件描述语言,用软件编程语言形式描述硬件电路功能,比原理图 方式更方便、更高效地反映电路的功能。 1.1逻辑代数基本概念、公式和定理 1.1.1基本和常用逻辑运算 教学目标: 1、理解3种基本逻辑运算的概念和对应的逻辑函数表达式: 2、理解逻辑函数的表达方式。 教学重点:基本逻辑运算。逻辑函数的表达方式。 教学难点:几种导出的逻辑运算的分析。(同或、异或) ·基本的逻辑关系:与、或、非三种逻辑。 ·数字系统中所有的逻辑关系均可以用基本的三种逻辑关系来实现(如同十进制数总 可以用10个数字和小数点表示出来一样) ·每一种基本逻辑关系对应一种逻辑运算。 一、三种基本逻辑运算 L.“与”逻辑关系 逻辑状态表 A 逻辑表达式:Y=A·B
数字电子技术-第一章逻辑代数 6 总之:数是用于计算的,而码是人为规定的 (25)10=(11001)2=(19)16 (25)10=(0010 0101)BCD (0101 1001)BCD=(59)10 (0101 1001)2=(89)10 四、EDA 技术(后续详细介绍) 一种以计算机作为工作平台,以 EDA 软件工具为开发环境,以 VHDL 为设计语 言,以可编程逻辑器件为实验载体,以 ASIC、SoC 芯片为目标器件,以数字系统设计 为应用方向的电子产品自动化设计技术。 VHDL 是一种硬件描述语言,用软件编程语言形式描述硬件电路功能,比原理图 方式更方便、更高效地反映电路的功能。 1. 1 逻辑代数基本概念、公式和定理 1. 1. 1 基本和常用逻辑运算 教学目标: 1、理解 3 种基本逻辑运算的概念和对应的逻辑函数表达式; 2、理解逻辑函数的表达方式。 教学重点:基本逻辑运算。逻辑函数的表达方式。 教学难点:几种导出的逻辑运算的分析。(同或、异或) ·基本的逻辑关系:与、或、非三种逻辑。 ·数字系统中所有的逻辑关系均可以用基本的三种逻辑关系来实现(如同十进制数总 可以用 10 个数字和小数点表示出来一样)。 ·每一种基本逻辑关系对应一种逻辑运算。 一、三种基本逻辑运算 1. “与”逻辑关系 逻辑状态表 逻辑表达式:Y = A • B A B Y 0 0 1 1 0 1 0 1 0 0 0 1
数字电子技术第一章逻辑代数 逻辑符号: 2.“或”逻辑关系 逻辑状态表: A B 0 逻辑表达式:Y=A+B 逻辑符号: 3.“非”逻辑关系 逻辑状态表: 逻辑表达式:y=A 巴 逻辑符号: 10 二、逻辑变量与逻辑函数及常用复合逻辑运算 0与非运算y-AB一一有0”出“1”,全“1”出0 @或非运算Y=A+B一一有“1”出0”,全0”出1” ③与或非运算Y=AB+CD 和0 O异或运算Y=A©B=AB+AB
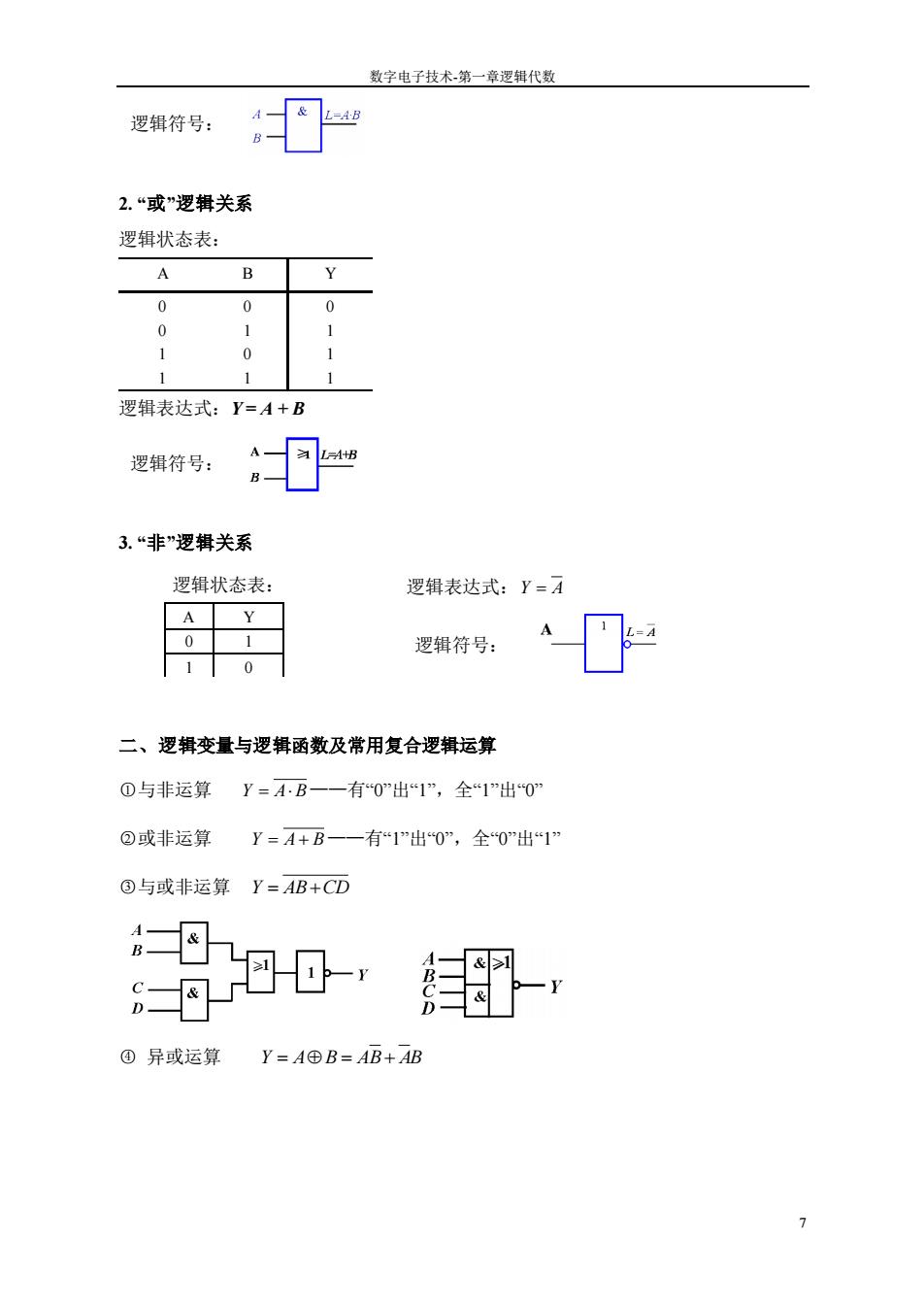
数字电子技术-第一章逻辑代数 7 2. “或”逻辑关系 逻辑状态表: A B Y 0 0 1 1 0 1 0 1 0 1 1 1 逻辑表达式:Y = A + B 3. “非”逻辑关系 逻辑表达式: Y A = 二、逻辑变量与逻辑函数及常用复合逻辑运算 ○1 与非运算 Y A B = ——有“0”出“1”,全“1”出“0” ○2 或非运算 Y A B = + ——有“1”出“0”,全“0”出“1” ○3 与或非运算 Y AB CD = + ○4 异或运算 Y A B AB AB = = + 逻辑符号: 逻辑符号: 逻辑符号: 逻辑状态表: A Y 0 1 1 0

数字电子技术.第一章逻辑代数 A BY 110 ⑤同或运算Y,=A田B=AB+AB 三、基本和常用逻辑运算的逻辑符号P11页 1.1.2公式和定理 教学目标: 1、掌握逻辑代数的基本公式。 2、理解逻辑代数的基本定律。 教学重点:逻辑代数的基本定律。 教学难点: 对逻辑运算以及基本公式的深入理解, 逻辑代数的基本定律的理解。 一、逻辑代数运算定理和法则 1常量和常量 2常量和变量、变量和变量 3、常用定律 结合律A+(B+C)=(A+B)+C A·(B·C)=(A·B)C 交换律A+B=B+AA·B=B·A 分配律A·(B+C)=A·B+AC A+B·C=(A+B)(A+C) 反演律(摩根定理)AB=A+BA+B=AB 4逻辑代数的两个重要规则 ①代入规则:在任何一个包含变量A逻辑等式中,如果用另一个函数式代入式中A 的位置,则等式仍然成立。这一规则称为代入规则。 例:已知等式B=A+B,利用代入规则,用函数Y=AC代替等式中的A。 解:根据代入规则,等式仍然成立,即有:(ACB=AC+B=A+B+
数字电子技术-第一章逻辑代数 8 ○5 同或运算 Y A B AB AB 5 = = + 三、基本和常用逻辑运算的逻辑符号 P11 页 1. 1. 2 公式和定理 教学目标: 1、掌握逻辑代数的基本公式。 2、理解逻辑代数的基本定律。 教学重点:逻辑代数的基本定律。 教学难点: 对逻辑运算以及基本公式的深入理解。 逻辑代数的基本定律的理解。 一、 逻辑代数运算定理和法则 1 常量和常量 2 常量和变量、变量和变量 3、常用定律 结合律 A + ( B + C)= (A + B) +C A (B C) = (A B) C 交换律 A + B = B + A A B = B A 分配律 A (B + C) = A B +A C A + B C= (A + B) (A + C) 反演律(摩根定理) A B A B = + A B A B + = 4 逻辑代数的两个重要规则 ○1 代入规则: 在任何一个包含变量 A 逻辑等式中,如果用另一个函数式代入式中 A 的位置,则等式仍然成立。这一规则称为代入规则。 例:已知等式 AB = A + B ,利用代入规则,用函数 Y=AC 代替等式中的 A。 解:根据代入规则,等式仍然成立,即有: ( ) AC B AC B A B C = + = + +

数字电子技术第一章逻辑代数 ②反演规则: 对于任意一个逻辑表达式,若将其中所有的与(•)换成或(+),或(+)换成与(·): 原变量换为反变量,反变量换为原变量:将1换成0,0换成1;则得到的结果就 是原函数的反函数 【例1-2】已知Y=AB+CDE,Y=A+B+C+D+E,利用反演规则求T 解: Y=AB+CDE -=(+BXC+D+E) Y=A+B+C+D+E-Y=A.B.C.D.E 12逻辑函数的化简方法 化简的主要方法:1.公式法(代数法):2.图形法(卡诺图法): 教学目标: 1、理解逻辑代数的基本规则。 2、熟悉基本规则的应用。 教学重点: 基本规则的理解。 对逻辑代数基本公式、规则的熟练应用。 教学难点:反演规则的应用。 1.2.1逻辑函数的标准与或式和最简式 一,最小项 定义:乘积项,每个变量均出现且只出现一次。 最小项是一种特殊的乘积项(“与”项),最小项具有一下特点: 1,n变量逻辑函数的最小项,一定包含n个因子: 2.在各个最小项中,每个变量以原变量和反变量的形式作为因子仅出现一次。 根据上述特点,容易写出两变量逻辑函数F(A,B)的最小项为,AB,A, AB:三变量逻辑函数F(A,B,C)的所有最小项为C,C,BC,BC,ABC, ABC,ABC,ABC共八项。不难看出,n变量逻辑函数最多有2个最小项。一般常对 最小项进行编号,记为m。这里m表示最小项,i是代号,且i=0,122”-l,n为变量 个数。三变量A,B,C构成的全部最小项的编号表和真值表如表11和表1-2所示 表11三变量最小项编号表 最小项使最小项为1的变量取值对应的十进制数编号
数字电子技术-第一章逻辑代数 9 ○2 反演规则: 对于任意一个逻辑表达式 L,若将其中所有的与(•)换成或(+),或(+)换成与(•); 原变量换为反变量,反变量换为原变量;将 1 换成 0,0 换成 1 ;则得到的结果就 是原函数的反函数。 【例 1-2】已知 Y = AB + CDE ,Y = A+ B +C + D + E ,利用反演规则求 Y 。 解: Y = AB + CDE Y = (A + B)(C + D + E) Y = A+ B +C + D + E Y = A B C D E 1.2 逻辑函数的化简方法 化简的主要方法:1.公式法(代数法); 2.图形法(卡诺图法); 教学目标: 1、理解逻辑代数的基本规则。 2、熟悉基本规则的应用。 教学重点: 基本规则的理解。 对逻辑代数基本公式、规则的熟练应用。 教学难点:反演规则的应用。 1. 2. 1 逻辑函数的标准与或式和最简式 一.最小项 定义:乘积项,每个变量均出现且只出现一次。 最小项是一种特殊的乘积项(“与”项),最小项具有一下特点: 1.n 变量逻辑函数的最小项,一定包含 n 个因子; 2. 在各个最小项中,每个变量以原变量和反变量的形式作为因子仅出现一次。 根据上述特点,容易写出两变量逻辑函数 F(A,B)的最小项为 AB ,AB ,AB , AB ;三变量逻辑函数 F(A,B,C)的所有最小项为 ABC ,ABC ,ABC ,ABC ,ABC , ABC, ABC, ABC 共八项。不难看出,n 变量逻辑函数最多有 2 n 个最小项。一般常对 最小项进行编号,记为 mi 。这里 m 表示最小项,i 是代号,且 0,1,2.2 1, n i n = − 为变量 个数。三变量 A,B,C 构成的全部最小项的编号表和真值表如表 1-1 和表 1-2 所示。 表 1-1 三变量最小项编号表 最小项 使最小项为 1 的变量取值 对应的十进制数 编号

数字电子技术.第一章逻辑代数 B ABC ARC ABC ABC ABC m 克1.2 三变量最小项真值表 B C 0 0 1 0 0 1 0 0 0 1 1 0 11 1000 0 0 0 0 由表1-2可以看出最小项具有一下性质。 a、每个最小项只有对应的一组变量取值能使其值为1。例如最小项C(m)只和“001” 这组取值对应,即只有当ABC取值为OO1时,最小项C才为1。变量取其他各组值时 最小项C的值皆为0。正因为这种“与”函数真值表中1的个数最小,所以“最小项 由此得名。 b、n个变量的全体最小项(共有2”个)之和恒为1,即艺%=1。 c、个变量的任意两个不同的最小项之积恒为0,即mm,=0,1≠j。这是因为变量的每组 取值,对于任何两个不同的最小项不能同时为1。 d、相邻的两个最小项之和,可以合并成一项(等于相同因子之积),并消去一个因子。 这里的“相邻”不是几何位置的相邻,而是指逻辑上的相邻。即两个最小项中只有一个因子 不同。 二、标准与或表达式 (1)标准与或表达式(最小项之和表达式):在与或”式中的每个乘积项都是最小项。 例1:将L(A,B,C)=AB+AC化成标准与或表达式 L(A.B,C)=AB(C+C)+(B+B)C ABC+ABC+ABC+ABC 例2:写出下列函数的标准与或式:
数字电子技术-第一章逻辑代数 10 表 1-2 三变量最小项真值表 A B C m0 m1 m2 m3 m4 m5 m6 m7 ABC ABC ABC ABC ABC ABC ABC ABC 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 1 由表 1-2 可以看出最小项具有一下性质。 a、 每个最小项只有对应的一组变量取值能使其值为 1。例如最小项 ABC ( m1 )只和“001” 这组取值对应,即只有当 ABC 取值为 001 时,最小项 ABC 才为 1。变量取其他各组值时, 最小项 ABC 的值皆为 0。正因为这种“与”函数真值表中 1 的个数最小,所以“最小项” 由此得名。 b、 n 个变量的全体最小项(共有 2 n 个)之和恒为 1,即 2 1 0 1 n i i m − = = 。 c、 n 个变量的任意两个不同的最小项之积恒为 0,即 0, m m i j i j = 。这是因为变量的每组 取值,对于任何两个不同的最小项不能同时为 1。 d、 相邻的两个最小项之和,可以合并成一项(等于相同因子之积),并消去一个因子。 这里的“相邻”不是几何位置的相邻,而是指逻辑上的相邻。即两个最小项中只有一个因子 不同。 二、标准与或表达式 (1)标准与或表达式(最小项之和表达式):在“与或”式中的每个乘积项都是最小项。 例 1:将 L A B C AB AC ( , , ) = + 化成标准与或表达式 L A B C AB C C A B B C ( , , ) ( ) ( ) = + + + = + + + ABC ABC ABC ABC 例 2:写出下列函数的标准与或式: A B C ABC 0 0 0 0 m0 ABC 0 0 1 1 m1 ABC 0 1 0 2 m2 ABC 0 1 1 3 m3 ABC 1 0 0 4 m4 ABC 1 0 1 5 m5 ABC 1 1 0 6 m6 ABC 1 1 1 7 m7