
第12卷第2期 智能系统学报 Vol.12 No.2 2017年4月 CAAI Transactions on Intelligent Systems Apr.2017 D0I:10.11992/is.201612038 网络出版地址:http://kns.cnki.net/kcms/detail/23.1538.TP.20170317.1937.020.html 模型切换抑制振荡误差在无人潜艇导航中的应用 王奎民,郭占军 (中国人民解放军驻锦州地区军事代表室,辽宁锦州121000) 摘要:导航的准确程度是无人潜艇执行任务的前提条件。由于长时间航行的无人潜艇,特别是有隐蔽性需求的无人 潜艇,其导航中存在的舒勒振荡的问题,会导致无人潜艇导航定位系统的存在定位误差。为得到精确的导航结果,必须 对振荡误差加以抑制。然而,传统单一的抑制方法中由于辅助信息存在应用范围的限制,不能满足全航程无人潜艇对 于导航精度的需求。因而本文提出了模型切换抑制振荡误差的方法。针对不同铺助信息适用的范围,采用不同的抑制 方式,提出了差分外测速度阻尼、相移抑制、GPS辅助相切换的振荡误差抑制方法,克服了传统方法的局限与不足。3 种方法在各自的适用范围内都能达到需要的精度,在长航程的无人潜艇航行过程中达到了抑制振荡误差的目的。仿真 实验说明了这种方法的有效性。模型切换抑制振荡误差的方法,可以提高无人潜艇的导航精度。 关键词:无人;潜艇:振荡阻尼;模型切换调节:导航:多普勒声呐:全球定位系统;捷联惯导 中图分类号:TP18:U666文献标志码:A文章编号:1673-4785(2017)02-0250-08 中文引用格式:王奎民,郭占军.模型切换抑制振荡误差在无人潜艇导航中的应用[J].智能系统学报,2017,12(2):250-257. 英文引用格式:WANG Kuimin,GUO Zhanjun..Application of model switching to suppress oscillation error in unmanned submarine navigation[J].CAAI transactions on intelligent systems,2017,12(2):250-257. Application of model switching to suppress oscillation error in unmanned submarine navigation WANG Kuimin,GUO Zhanjun (Navy Military Representative Office in Jinzhou,Jinzhou 121000,China) Abstract:Precise navigation is the basis for task completion in unmanned submarines.Oscillation error exists in un- manned submarines with long voyage missions,in particular,with the missions serving military purposes,which leads to navigation error.For obtaining accurate navigation results,the oscillation error must be suppressed.Howev- er,owing to the restrictions in the traditional single algorithm,the accuracy requirements cannot be met in the en- tire process of navigation.Therefore,in this study,a model switching method to suppress the oscillation error in un- manned submarine navigations is proposed.Different oscillation-error-suppression methods were used for different application scopes.Differential Doppler external velocity damping assisting,phase shift inhibition assisting,and GPS assisting were presented in the model switching method that overcame the limitations of the traditional methods. This method can suppress the oscillation error during sailing and thus meet the accuracy requirement essential dur- ing unmanned submarine navigation.Simulation results show the effectiveness of this method.The model switching method is found to effectively improve navigation accuracy. Keywords:unmanned vehicles;submarine;oscillation damping;model switching regulators;navigation;Doppler sonar;GPS;SINS 收稿日期:2016-12-30.,网络出版日期:2017-03-17. 无人潜艇具有重要的军事用途和广泛的商业用 基金项目:国家自然科学基金项目(51679057). 通信作者:王奎民.E-mail:wangkuimin@163.com 途。在国家海防建设以及失事飞机搜寻的方面有着 重要的应用。精准的导航方法是无人潜艇完成各项
第 12 卷第 2 期 智 能 系 统 学 报 Vol.12 №.2 2017 年 4 月 CAAI Transactions on Intelligent Systems Apr. 2017 DOI:10.11992 / tis.201612038 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170317.1937.020.html 模型切换抑制振荡误差在无人潜艇导航中的应用 王奎民,郭占军 (中国人民解放军驻锦州地区军事代表室,辽宁 锦州 121000) 摘 要:导航的准确程度是无人潜艇执行任务的前提条件。 由于长时间航行的无人潜艇,特别是有隐蔽性需求的无人 潜艇,其导航中存在的舒勒振荡的问题,会导致无人潜艇导航定位系统的存在定位误差。 为得到精确的导航结果,必须 对振荡误差加以抑制。 然而,传统单一的抑制方法中由于辅助信息存在应用范围的限制,不能满足全航程无人潜艇对 于导航精度的需求。 因而本文提出了模型切换抑制振荡误差的方法。 针对不同辅助信息适用的范围,采用不同的抑制 方式,提出了差分外测速度阻尼、相移抑制、GPS 辅助相切换的振荡误差抑制方法,克服了传统方法的局限与不足。 3 种方法在各自的适用范围内都能达到需要的精度,在长航程的无人潜艇航行过程中达到了抑制振荡误差的目的。 仿真 实验说明了这种方法的有效性。 模型切换抑制振荡误差的方法,可以提高无人潜艇的导航精度。 关键词:无人;潜艇;振荡阻尼;模型切换调节;导航;多普勒声吶;全球定位系统;捷联惯导 中图分类号: TP18;U666 文献标志码:A 文章编号:1673-4785(2017)02-0250-08 中文引用格式:王奎民,郭占军. 模型切换抑制振荡误差在无人潜艇导航中的应用[J]. 智能系统学报, 2017, 12(2): 250-257. 英文引用格式:WANG Kuimin, GUO Zhanjun. Application of model switching to suppress oscillation error in unmanned submarine navigation[J]. CAAI transactions on intelligent systems, 2017, 12(2): 250-257. Application of model switching to suppress oscillation error in unmanned submarine navigation WANG Kuimin, GUO Zhanjun (Navy Military Representative Office in Jinzhou, Jinzhou 121000, China) Abstract:Precise navigation is the basis for task completion in unmanned submarines. Oscillation error exists in un⁃ manned submarines with long voyage missions, in particular, with the missions serving military purposes, which leads to navigation error. For obtaining accurate navigation results, the oscillation error must be suppressed. Howev⁃ er, owing to the restrictions in the traditional single algorithm, the accuracy requirements cannot be met in the en⁃ tire process of navigation. Therefore, in this study, a model switching method to suppress the oscillation error in un⁃ manned submarine navigations is proposed. Different oscillation⁃error⁃suppression methods were used for different application scopes. Differential Doppler external velocity damping assisting, phase shift inhibition assisting, and GPS assisting were presented in the model switching method that overcame the limitations of the traditional methods. This method can suppress the oscillation error during sailing and thus meet the accuracy requirement essential dur⁃ ing unmanned submarine navigation. Simulation results show the effectiveness of this method. The model switching method is found to effectively improve navigation accuracy. Keywords:unmanned vehicles; submarine; oscillation damping; model switching regulators; navigation; Doppler sonar; GPS; SINS 收稿日期:2016-12-30. 网络出版日期 基金项目:国家自然科学基金项目(516790 :2 5 0 7 1 ) 7-03-17. 无人潜艇具有重要的军事用途和广泛的商业 通信作者:王奎民. E⁃mail:wangkuimin@ 163.com. 用 途。 在国家海防建设以及失事飞机搜寻的方面有着 重要的应用。 精准的导航方法是无人潜艇完成各项 .

第2期 王奎民,等:模型切换抑制振荡误差在无人潜艇导航中的应用 ·251. 复杂任务的前提。对于采用捷联惯导系统(strapdown 同时考虑到各种方法的应用局限:多普勒外测 inertial navigation system,SNS)或者基于SlNS的组 速度只有在靠近海底几十米的范围内才能得到准确 合导航系统而言,振荡误差对于系统的影响是不可忽 的速度信息:GPS只有在无人潜艇靠近水面十几米 略的。振荡主要包含周期为84.4min的舒勒振荡、傅 才能获得信号,但得到的信号十分准确;基于自身信 科振荡以及周期为24h的地球圆周振荡。尤其是对 号移相抑制方法不依赖外部辅助信息,但是由于振 于长航时隐蔽性和准确性要求较高的无人潜艇,这种 荡误差相位测量以及移相控制相对于有外部辅助信 振荡误差是随着时间积累并且不断发散的。 息的系统,不够准确。为了克服以上局限和缺点,充 为了抑制这种周期性的振荡误差,学者们主要 分发挥各种算法的优点,提出了以深度和高度为阈 采用内阻尼)和外阻尼[2-)两种形式。但内阻尼在 值的模型切换方法。根据航行需要,当无人潜艇靠 抑制误差的同时,系统的速度及加速度会对失准角 近水面时,采用GPS信号辅助抑制振荡误差;当无 产生一定的干扰。针对内阻尼网络的不足,又提出 人潜艇靠近海底,可以获得准确且稳定的多普勒外 了外测速度阻尼网络的抑制方法,但这种方法仍存 测速度信号时,采用差分的外测速度阻尼网络抑制 在局限性,对于振荡误差的抑制效果完全取决于外 振荡误差:当无人潜艇在中等深度航行,既无法获得 测速度的精度。文献[2]提出了将3种不同的阻尼 GPS信号,同时多普勒测得的速度信息还不准确的 反馈到3个循环中,由于速度阻尼使得系统更加敏 时候,就采取自身移相抑制方法抑制振荡误差。 感,参数设计十分复杂,并且文章中的算法主要适用 于水面舰船,不适用于水下的无人潜艇:文献[3]将 1无人潜艇导航模型 外测速度阻尼的方法改进提出了一种混合阻尼的方 首先定义相关的基本坐标系:i系一地心惯性 法,但阻尼算法对振荡的抑制效果仍依赖外测速度 坐标系;e系一地心地固坐标系;n系一导航坐标 的准确程度:文献[4]提出了一种通过预测时间序 系:b系一载体坐标系。 列来预测振荡趋势抑制振荡误差的方法,该方法的 根据捷联惯导原理,分别建立无人潜艇姿态、速 优点在于不依赖外部的速度、位置等辅助信息,完全 度和位置更新方程,即为无人潜艇导航模型。 依赖自身对于振荡的预测进行抑制,应用范围较广 1.1无人潜艇姿态更新方程 泛,但相对于可以得到准确速度位置信息的系统,振 荡误差的抑制效果较差;文献[5]提出了以外部速 C=CR (1) 度测量作为参考的基于卡尔曼滤波的最优阻尼算 w=ω-wn=w品-Ctw (2) 法,基于最优控制的思想,反馈校正了舒勒振荡和傅 w=w +a (3) 科振荡:文献[6]是在数字平台上实现阻尼网络,在 式中:C:是无人潜艇相对于b系转换到n系的转换 捷联惯导系统的航姿系统中引入传统的平台内阻 矩阵,ω是在b系下,n系相对于载体坐标系的旋 尼,为了较为简单的保证实时性,采用了模糊内阻尼 转角速度,w“是在b系下,i系相对于载体坐标系 系统;文献[7]将惯导系统速度作为参数引入水平 的旋转角速度,w是在n系下,i系相对于导航坐 通道控制回路,利用模糊控制器估计系统的实时速 度,设计了二阶阻尼网络达到了抑制误差的目的:文 标系的旋转角速度,w是在n系下,i系相对于e系 献[8]设计了一种单通道水平网络自适应控制系 的旋转角速度,ω是在n系下,e系相对于n系的 统,以定位误差的振荡峰值为自适应控制的目标函 旋转角速度。 数,确立了阻尼网络的阻尼系数关于加速度变化量 1.2无人潜艇速度更新方程 的优化函数。 捷联惯导系统向量形式的基本方程为 由分析可知,目前研究中的抑制振荡误差的方 Vm=f-(2w+0m)×Vp+g (4) 法主要为利用外测速度信息对系统进行校正,抑制 式中:V,是无人潜艇相对于地球的加速度向量,∫ 效果主要取决于外测速度的准确程度,因而准确的 是加速度计所测得的经过坐标转换得到的比力, 外测速度信息对于基于外测速度阻尼网络而言是十 分重要的。本文在此想法基础上针对外测速度不准 (2ω+ωm)×Vm是地球自转和无人潜艇相对于地 确问题加以扩展和改进,提出了差分多普勒外测速 球运动产生的加速度,为了计算V要把它从∫中除 度,有效提高了外测速度的准确性,同时避免了某一 去,因为它是有害加速度,g是地球重力加速度。 个多普勒系统出现故障而使得系统瘫痪的问题。 根据式(4)可以得到捷联惯导系统的速度方程为
复杂任务的前提。 对于采用捷联惯导系统(strapdown inertial navigation system, SINS)或者基于 SINS 的组 合导航系统而言,振荡误差对于系统的影响是不可忽 略的。 振荡主要包含周期为 84.4 min 的舒勒振荡、傅 科振荡以及周期为 24 h 的地球圆周振荡。 尤其是对 于长航时隐蔽性和准确性要求较高的无人潜艇,这种 振荡误差是随着时间积累并且不断发散的。 为了抑制这种周期性的振荡误差,学者们主要 采用内阻尼[1]和外阻尼[2-8]两种形式。 但内阻尼在 抑制误差的同时,系统的速度及加速度会对失准角 产生一定的干扰。 针对内阻尼网络的不足,又提出 了外测速度阻尼网络的抑制方法,但这种方法仍存 在局限性,对于振荡误差的抑制效果完全取决于外 测速度的精度。 文献[2]提出了将 3 种不同的阻尼 反馈到 3 个循环中,由于速度阻尼使得系统更加敏 感,参数设计十分复杂,并且文章中的算法主要适用 于水面舰船,不适用于水下的无人潜艇;文献[3]将 外测速度阻尼的方法改进提出了一种混合阻尼的方 法,但阻尼算法对振荡的抑制效果仍依赖外测速度 的准确程度;文献[4]提出了一种通过预测时间序 列来预测振荡趋势抑制振荡误差的方法,该方法的 优点在于不依赖外部的速度、位置等辅助信息,完全 依赖自身对于振荡的预测进行抑制,应用范围较广 泛,但相对于可以得到准确速度位置信息的系统,振 荡误差的抑制效果较差;文献[5]提出了以外部速 度测量作为参考的基于卡尔曼滤波的最优阻尼算 法,基于最优控制的思想,反馈校正了舒勒振荡和傅 科振荡;文献[6]是在数字平台上实现阻尼网络,在 捷联惯导系统的航姿系统中引入传统的平台内阻 尼,为了较为简单的保证实时性,采用了模糊内阻尼 系统;文献[7]将惯导系统速度作为参数引入水平 通道控制回路,利用模糊控制器估计系统的实时速 度,设计了二阶阻尼网络达到了抑制误差的目的;文 献[8] 设计了一种单通道水平网络自适应控制系 统,以定位误差的振荡峰值为自适应控制的目标函 数,确立了阻尼网络的阻尼系数关于加速度变化量 的优化函数。 由分析可知,目前研究中的抑制振荡误差的方 法主要为利用外测速度信息对系统进行校正,抑制 效果主要取决于外测速度的准确程度,因而准确的 外测速度信息对于基于外测速度阻尼网络而言是十 分重要的。 本文在此想法基础上针对外测速度不准 确问题加以扩展和改进,提出了差分多普勒外测速 度,有效提高了外测速度的准确性,同时避免了某一 个多普勒系统出现故障而使得系统瘫痪的问题。 同时考虑到各种方法的应用局限:多普勒外测 速度只有在靠近海底几十米的范围内才能得到准确 的速度信息;GPS 只有在无人潜艇靠近水面十几米 才能获得信号,但得到的信号十分准确;基于自身信 号移相抑制方法不依赖外部辅助信息,但是由于振 荡误差相位测量以及移相控制相对于有外部辅助信 息的系统,不够准确。 为了克服以上局限和缺点,充 分发挥各种算法的优点,提出了以深度和高度为阈 值的模型切换方法。 根据航行需要,当无人潜艇靠 近水面时,采用 GPS 信号辅助抑制振荡误差;当无 人潜艇靠近海底,可以获得准确且稳定的多普勒外 测速度信号时,采用差分的外测速度阻尼网络抑制 振荡误差;当无人潜艇在中等深度航行,既无法获得 GPS 信号,同时多普勒测得的速度信息还不准确的 时候,就采取自身移相抑制方法抑制振荡误差。 1 无人潜艇导航模型 首先定义相关的基本坐标系: i 系—地心惯性 坐标系; e 系—地心地固坐标系; n 系—导航坐标 系; b 系—载体坐标系。 根据捷联惯导原理,分别建立无人潜艇姿态、速 度和位置更新方程,即为无人潜艇导航模型。 1.1 无人潜艇姿态更新方程 C ·n b = C n bω b nb (1) ω b nb = ω b ib - ω b in = ω b ib - C b nω n in (2) ω n in = ω n ie + ω n en (3) 式中: C n b 是无人潜艇相对于 b 系转换到 n 系的转换 矩阵, ω b nb 是在 b 系下, n 系相对于载体坐标系的旋 转角速度, ω b ib 是在 b 系下, i 系相对于载体坐标系 的旋转角速度, ω n in 是在 n 系下, i 系相对于导航坐 标系的旋转角速度, ω n ie 是在 n 系下, i 系相对于 e 系 的旋转角速度, ω n en 是在 n 系下, e 系相对于 n 系的 旋转角速度。 1.2 无人潜艇速度更新方程 捷联惯导系统向量形式的基本方程为 V · ep = f - (2ωie + ωep) × Vep + g (4) 式中: V · ep 是无人潜艇相对于地球的加速度向量, f 是加速度计所测得的经过坐标转换得到的比力, - (2ωie + ωep) × Vep 是地球自转和无人潜艇相对于地 球运动产生的加速度,为了计算 V · ep 要把它从 f 中除 去,因为它是有害加速度, g 是地球重力加速度。 根据式(4)可以得到捷联惯导系统的速度方程为 第 2 期 王奎民,等:模型切换抑制振荡误差在无人潜艇导航中的应用 ·251·

.252. 智能系统学报 第12卷 1 v =f+(20.sin L+V,tan LR)V,- Ms= Ro2 0e+ 6V0 0 Ro (2 cos L+V/Rn)·V: (5) 1 N2= V,=f,-(20sin L+V,tan L/R)V.- V.V./R 1 N3= eg+sinpΦo-cospΦo 式中ω是地球自转角速度。 1.3无人潜艇位置更新方程 cos Ev+ 艺6。+Φm+δp。 根据捷联惯导中,n系与地球坐标系的关系知: N3 sing L= ie g (6) 式中:w是地球旋转角速率;ω,为舒勒振荡频率; R是地球半径;g是重力加速度;p是纬度;8VE, Rcos L 8V、分别是东向和北向速度误差:δp是纬度误差; 式中:L、入为经纬度,V和V,分别为无人潜艇的 Φe、Φ、Φ,分别是东向,北向和天向3个方向上的 东向和北向速度。 角度误差;又。、V、分别为东向加速度计和北向加速 (R =R(1 esin 2L)+h (7) 度计的加速度漂移;Eε、ew、su分别为东向、北向和 R =R(1-2e +3esin2L)+h 天向陀螺仪的陀螺漂移。 式中R,和R.分别表示无人潜艇所在位置地球曲率 通过式(8)和(9)可以看出,尽管在稳定状态 半径。 下,舒勒振荡误差以及地球周期振荡误差仍然包含 2振荡误差及其对无人潜艇的影响 在中。和6L中。从数学的角度来看,这些振荡误差 可以看作是一些正弦函数和余弦函数叠加得到的。 惯性导航系统有着随时间不断累积的误差,初 始对准的误差、陀螺和加速度计的测量误差等导致 3 模型切换方法抑制振荡误差 了系统产生3种典型的振荡误差,其中舒勒振荡误 传统捷联惯导系统振荡误差存在并不断累积,对 差将会对系统产生主要影响,其次是与其调制的傅 于应用捷联惯导系统作为主要导航方式的无人潜艇 科振荡误差,而地球圆周振荡误差相对于前两者,对 而言,在水下是十分危险的。然而对于各种外部辅助 系统影响最小。这些振荡误差大大降低了惯性导航 信息抑制振荡误差的方法,各自有各自的优缺点,如 系统的精度9-0。这对于在水下航行,尤其是长时 何将各种方法融合,并将误差抑制效果达到最佳,是 间在水下航行的无人潜艇来说,由于误差不断累积, 模型切换山方法提出的主要目的。 就不断偏离预定的航行位置,即使在已知海况的海 对于振荡误差抑制的3种主要方法,即差分外测 域也将存在被撞毁的危险。因而对于振荡误差的抑 速度阻尼抑制方法、移相抑制方法以及GS辅助抑 制是十分重要的4)。 制方法。模型切换抑制振荡误差的原理图如图1。 以东向角度误差④和纬度误差δL为例,文献 差分多普勒外 [4]给出了其误差表达形式: 移相辅助 位置辅助 测速度辅助 Φe(t)=M1sinw,t+M2cosω,t+ M3sin @t Macos @it Ms 判断深度及高度 (8) 速度 SL(t)=N sin @t N,cos @t+ 姿态传感器 Nasin @t Ncos @t Ns (9) 捷联惯导 角度 式中: 系统 深度 滤波 9 压力传感器 位置 估计 ωia 1 + M,=- e,+。+R 位置传感器 图1模型切换抑制振荡误差原理图 ie M3=- e+m Fig.1 Principle diagram of model switching method to w suppress oscillation error
V · x = fx + (2ωie sin L + Vx tan L / Rn )·Vy - (2ωie cos L c + Vx / Rn )·Vz V · y = fy - (2ωie sin L + Vx tan L / Rn )·Vx - VyVz / Rm ì î í ï ï ï ï ï ï (5) 式中 ωie 是地球自转角速度。 1.3 无人潜艇位置更新方程 根据捷联惯导中, n 系与地球坐标系的关系知: L · = Vy Rm λ · = Vx Rn cos L ì î í ï ïï ï ïï (6) 式中: L 、 λ 为经纬度, Vx 和 Vy 分别为无人潜艇的 东向和北向速度。 Rn = R(1 + esin 2 L) + h Rm = R(1 - 2e + 3esin 2 { L) + h (7) 式中 Rn 和 Rm 分别表示无人潜艇所在位置地球曲率 半径。 2 振荡误差及其对无人潜艇的影响 惯性导航系统有着随时间不断累积的误差,初 始对准的误差、陀螺和加速度计的测量误差等导致 了系统产生 3 种典型的振荡误差,其中舒勒振荡误 差将会对系统产生主要影响,其次是与其调制的傅 科振荡误差,而地球圆周振荡误差相对于前两者,对 系统影响最小。 这些振荡误差大大降低了惯性导航 系统的精度[9-10] 。 这对于在水下航行,尤其是长时 间在水下航行的无人潜艇来说,由于误差不断累积, 就不断偏离预定的航行位置,即使在已知海况的海 域也将存在被撞毁的危险。 因而对于振荡误差的抑 制是十分重要的[4] 。 以东向角度误差 ΦE 和纬度误差 δL 为例,文献 [4]给出了其误差表达形式: ΦE (t) = M1 sin ωs t + M2 cos ωs t + M3 sin ωie t + M4 cos ωie t + M5 (8) δL(t) = N1 sin ωs t + N2 cos ωs t + N3 sin ωie t + N4 cos ωie t + N5 (9) 式中: M1 = 1 ωs εE - 1 Rωs δVN0 M2 = - ω z iet ω 2 s εN + ω y iet ω 2 s εU + ΦE0 + 1 Rω 2 s ÑN M3 = - ωie ω 2 s ε E ;M4 = ω z iet ω 2 s εN - ω y iet ω 2 s εU + ΦE0 M5 = 1 Rω 2 s ÑN ;N1 = - 1 ωs εE + 1 Rωs δVN0 N2 = ω z iet ω 2 s εN - ω y iet ω 2 s εU - ΦE0 - 1 Rω 2 s ÑN N3 = 1 ωie εE + sin φΦN0 - cos φΦN0 N4 = sin φ ωie εN + cos φ ωie εU + ΦE0 + δφ0 N5 = sin φ ωie εE + cos φ ωie εU + ÑN g 式中: ωie 是地球旋转角速率; ωs 为舒勒振荡频率; R 是地球半径; g 是重力加速度; φ 是纬度; δVE , δVN 分别是东向和北向速度误差; δφ 是纬度误差; ΦE 、ΦN、ΦU 分别是东向,北向和天向 3 个方向上的 角度误差; ÑE 、ÑN 分别为东向加速度计和北向加速 度计的加速度漂移; ε E 、ε N、ε U 分别为东向、北向和 天向陀螺仪的陀螺漂移。 通过式(8) 和(9) 可以看出,尽管在稳定状态 下,舒勒振荡误差以及地球周期振荡误差仍然包含 在 ΦE 和 δL 中。 从数学的角度来看,这些振荡误差 可以看作是一些正弦函数和余弦函数叠加得到的。 3 模型切换方法抑制振荡误差 传统捷联惯导系统振荡误差存在并不断累积,对 于应用捷联惯导系统作为主要导航方式的无人潜艇 而言,在水下是十分危险的。 然而对于各种外部辅助 信息抑制振荡误差的方法,各自有各自的优缺点,如 何将各种方法融合,并将误差抑制效果达到最佳,是 模型切换[11]方法提出的主要目的。 对于振荡误差抑制的 3 种主要方法,即差分外测 速度阻尼抑制方法、移相抑制方法以及 GPS 辅助抑 制方法。 模型切换抑制振荡误差的原理图如图 1。 图 1 模型切换抑制振荡误差原理图 Fig.1 Principle diagram of model switching method to suppress oscillation error ·252· 智 能 系 统 学 报 第 12 卷

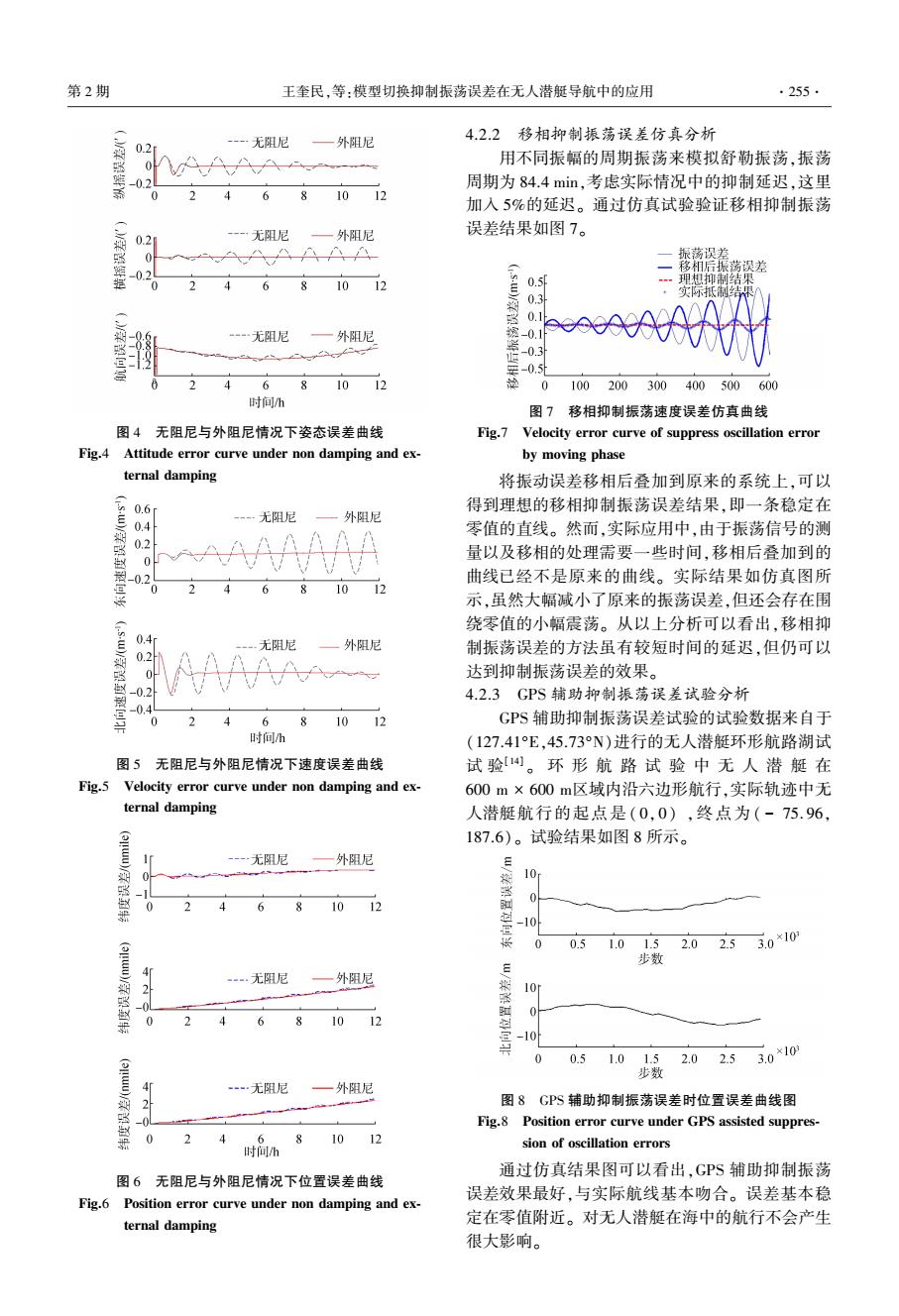
第2期 王奎民,等:模型切换抑制振荡误差在无人潜艇导航中的应用 .253 对于3种抑制振荡误差的算法,本着抑制误差 [1-H,(s)] 效果最佳的原则,以深度为评价指标,采用模型切换 α(s)= V,(s)+ R[s2 +H(s)@2] 的方法。在水面及水面以下10m内是可以准确地 [1-H,(s)] 接收到GPS信号的,因而在这段深度范围内采取 (10) R[s2+H,(s)02] ·s·o(s) GPS辅助抑制振荡误差的方法:在靠近海底30m以 由式(10)可见,无人潜艇导航定位中的水平失 内,是可以通过差分多普勒准确地获得外测速度信 准角[的造成的动态误差会随着无人潜艇的速度和 息的],因而在这段高度范围内,采用差分多普勒 加速度的增大而增大。 辅助抑制方法:在既不属于水面以下10m以内,也 当外测速度信息被引入到系统当中时,系统的 不属于靠近海底30m以内位置时,既无法获得准确 传递函数如下: 的位置信号,也无法获得准确的差分多普勒外测速 度信息,因而采取自身移相抑制振荡误差。 a(s)=Q{[1-H(s)]-[1-H,(s)]}V,(s)+ 同时考虑无人潜艇在较浅海域航行时,可能既 Q{[1-H,(s)]-[1-H,(s)]}·s·V,o(s)- 满足水面以下10m以内,同时也满足距离海底30m Qs…2[W()+V.)] (11) 以内,这是本着辅助信息最准确的原则,优先选择 GPS位置辅助信息抑制的方法。确定辅助抑制振荡 式中Q=1/R[s2+H,(s)ω]。 误差的方法后,采用改进的自适应滤波算法[)],对 通过上面的分析可知引入外测速度信息可以有 测得的信息以及已知信息融合,反馈到捷联惯导系 效的解决加入水平阻尼的问题,因为随着差分外测速 度信息的引入,加速度和速度产生的误差项已经不存 统中,获得更加准确的输出。 在于动态误差的式子中。而外测速度信息的准确程 通过以上方式,克服了3种误差抑制方法的不 度直接影响系统能否彻底消除振荡误差。实际上外 足,即多普勒在距离海底超过一定距离后,无法获得 测速度的信息是存在误差的,因而提出了差分多普勒 准确的外测速度信息:当在水下较深时,由于无线电 信号在水下无法传播,无法获得GPS位置信号,而 的形式,目的是得到更加准确的外测速度信息。 应用移相抑制振荡误差方法,虽可以抑制部分确定 式(11)表明,失准角a(s)与速度V,(s)以及 的振荡误差,但由于系统在运行时,会存在短时间处 加速度V,(s)无关,从而可知在引入外测速度阻尼 理延迟以及一些随时间无规律的随机振荡误差,因 后,系统的速度和加速度将不会对系统的失准角 而对于这部分误差的抑制效果并不好。而将三者结 α(s)产生影响。失准角α(s)仅与外测速度误差 合,可以充分发挥3种误差抑制方法的准确性,将达 到准确抑制振荡误差的目的。 2V,(s)+V(s)】有关,并且会随着外测速度 3.1差分外测速度阻尼 误差的增加而增加,因而有效抑制了系统自身速度 对文献[14]中的外测速度阻尼改进,引入差分 和加速度对于系统的影响,通过差分得到的外测速 多普勒外测速度的思想,利用多普勒测得的外测速 度的信息使得外测速度的辅助信息更加精确。 度构成阻尼网络的输入V,令阻尼网络为[1- 3.2移相抑制振荡方法 H,(s)],加入到捷联惯导通道中形成多普勒外测速 从第1部分可以看出,捷联惯导系统所涉及的 度阻尼系统,得到系统的流程图如图2所示: 振荡误差从数学的角度来分析是一些正弦波和余弦 △C(s) AV (s) 波的叠加。 (s)(s)(s) 为了简化问题的分析,考虑一个周期为T的周 -1111 期振荡函数为 (s) (s)s)(s)8o(s) a(s) y (t)=Asin (wt) (12) [1-H(s] 式中w=2π/T。 K(s) 另一个周期为T的周期振荡函数为 图2单通道差分外测速度阻尼系统流程图 0=naf+} Fig.2 Information flow chart of single channel horizon- (13) tal external damping system with differential Asin (wt +T)=-Asin (wt) DVL 整理方程(12)和方程(13)可以得到: 根据梅森增益公式,当外测速度的信息不被引 y)=四+与) 入到系统当中时,可以得到无人潜艇速度和加速度 2 (14) 对水平失准角a(s)的影响如式(10)所示: Asin (wt)-Asin (ot) =0 2
对于 3 种抑制振荡误差的算法,本着抑制误差 效果最佳的原则,以深度为评价指标,采用模型切换 的方法。 在水面及水面以下 10 m 内是可以准确地 接收到 GPS 信号的,因而在这段深度范围内采取 GPS 辅助抑制振荡误差的方法;在靠近海底 30 m 以 内,是可以通过差分多普勒准确地获得外测速度信 息的[12] ,因而在这段高度范围内,采用差分多普勒 辅助抑制方法;在既不属于水面以下 10 m 以内,也 不属于靠近海底 30 m 以内位置时,既无法获得准确 的位置信号,也无法获得准确的差分多普勒外测速 度信息,因而采取自身移相抑制振荡误差。 同时考虑无人潜艇在较浅海域航行时,可能既 满足水面以下 10 m 以内,同时也满足距离海底 30 m 以内,这是本着辅助信息最准确的原则,优先选择 GPS 位置辅助信息抑制的方法。 确定辅助抑制振荡 误差的方法后,采用改进的自适应滤波算法[13] ,对 测得的信息以及已知信息融合,反馈到捷联惯导系 统中,获得更加准确的输出。 通过以上方式,克服了 3 种误差抑制方法的不 足,即多普勒在距离海底超过一定距离后,无法获得 准确的外测速度信息;当在水下较深时,由于无线电 信号在水下无法传播,无法获得 GPS 位置信号,而 应用移相抑制振荡误差方法,虽可以抑制部分确定 的振荡误差,但由于系统在运行时,会存在短时间处 理延迟以及一些随时间无规律的随机振荡误差,因 而对于这部分误差的抑制效果并不好。 而将三者结 合,可以充分发挥 3 种误差抑制方法的准确性,将达 到准确抑制振荡误差的目的。 3.1 差分外测速度阻尼 对文献[14]中的外测速度阻尼改进,引入差分 多普勒外测速度的思想,利用多普勒测得的外测速 度构成阻尼网络的输入 Vxy ,令阻尼网络为 [1 - Hy(s)] ,加入到捷联惯导通道中形成多普勒外测速 度阻尼系统,得到系统的流程图如图 2 所示: 图 2 单通道差分外测速度阻尼系统流程图 Fig.2 Information flow chart of single channel horizon⁃ tal external damping system with differential DVL 根据梅森增益公式,当外测速度的信息不被引 入到系统当中时,可以得到无人潜艇速度和加速度 对水平失准角 α(s) 的影响如式(10)所示: α(s) = 1 - Hy [ (s) ] R s 2 + Hy (s) ω 2 s [ ] V · y (s) + 1 - Hy [ (s) ] R s 2 + Hy (s) ω 2 s [ ] ·s·Vy0 (s) (10) 由式(10)可见,无人潜艇导航定位中的水平失 准角[15]造成的动态误差会随着无人潜艇的速度和 加速度的增大而增大。 当外测速度信息被引入到系统当中时,系统的 传递函数如下: α(s) = Q 1 - Hy [ (s) ] - 1 - Hy { [ (s) ] } V · y (s) + Q 1 - Hy [ (s) ] - 1 - Hy { [ (s) ] }·s·Vy0 (s) - Q·s· δ 2 Vwy1 (s) + Vwy2 [ (s) ] (11) 式中 Q = 1 / R s 2 + Hy (s) ω 2 s [ ] 。 通过上面的分析可知引入外测速度信息可以有 效的解决加入水平阻尼的问题,因为随着差分外测速 度信息的引入,加速度和速度产生的误差项已经不存 在于动态误差的式子中。 而外测速度信息的准确程 度直接影响系统能否彻底消除振荡误差。 实际上外 测速度的信息是存在误差的,因而提出了差分多普勒 的形式,目的是得到更加准确的外测速度信息。 式(11)表明,失准角 α(s) 与速度 Vy (s) 以及 加速度 V · y (s) 无关,从而可知在引入外测速度阻尼 后,系统的速度和加速度将不会对系统的失准角 α(s) 产生影响。 失准角 α(s) 仅与外测速度误差 δ 2 [Vwy1(s) + Vwy2(s) ] 有关,并且会随着外测速度 误差的增加而增加,因而有效抑制了系统自身速度 和加速度对于系统的影响,通过差分得到的外测速 度的信息使得外测速度的辅助信息更加精确。 3.2 移相抑制振荡方法 从第 1 部分可以看出,捷联惯导系统所涉及的 振荡误差从数学的角度来分析是一些正弦波和余弦 波的叠加。 为了简化问题的分析,考虑一个周期为 T 的周 期振荡函数为 y1 (t) = Asin (ωt) (12) 式中 ω = 2π/ T 。 另一个周期为 T 的周期振荡函数为 y2 (t) = Asin ω t + T 2 æ è ç ö ø ÷ = Asin (ωt + π) = - Asin (ωt) (13) 整理方程(12)和方程(13)可以得到: y (t) = y1 (t) + y2 (t) 2 = Asin (ωt) - Asin (ωt) 2 = 0 (14) 第 2 期 王奎民,等:模型切换抑制振荡误差在无人潜艇导航中的应用 ·253·

,254 智能系统学报 第12卷 从方程(10)可以看出,振荡信号可以通过一个 这里针对无人潜艇捷联惯导系统的非线性特 相位相差π的幅值相等的信号进行抑制。因此,舒 性,通过容积卡尔曼滤波(CKF),对捷联惯导系统测 勒振荡信号以及地球周期振荡信号也可以通过相位 得的信息与外部接收的GPS信号信息进行融 相差为π的幅值相等的信号将其抑制。 合[]。容积卡尔曼滤波器的输入是惯导解算得到 通过研究可知,陀螺漂移是捷联惯导系统误差 的速度、位置和GPS解算得到的速度、位置,解算出 的主要来源,这种误差会激励舒勒振荡。 来的导航参数误差参数通过容积卡尔曼滤波器反馈 综合整理上式可得: 并修正捷联惯导直接计算出来的导航结果,容积卡 尔曼滤波器还将解算得到的加速度计、陀螺仪常值 T=2T R =84.4min (15) go 零偏反馈并修正捷联惯导的原始输出,实现对振荡 式(15)说明舒勒振荡是一个周期为84.4mim 误差的在线抑制1】」 的周期振荡,根据前面分析得到的结果,利用一个相 由于GPS信号稳定且准确,所组合输出得到的 位相差为π的幅值相等正余弦信号与舒勒振荡信 信息与系统实际运动的情况一致,所存在的微小误 号融合,可以对舒勒振荡进行抑制。 差就是GPS系统的误差。GPS辅助抑制振荡误差 由于振荡误差主要有陀螺仪以漂移以及加速度 的方法是抑制振荡误差效果最好的一种方法,但是 计漂移形成,并且受经纬度等诸多因素的影响。朱 由于GPS信号在水下只能传播较短距离,因而只有 行宜[16)设计了一种高精度相移信号发生器精度高 在无人潜艇靠近水面时可以使用。 且价格低廉,可有效解决相移信号的产生问题,通过 4仿真分析 防水密封等处理后,用在无人潜艇上。将监测到的 振荡信号输入高精度相移信号发生器,设置相移为 4.1仿真条件 π后,得到的输出信号与原测量信号中和达到抑制 分析差分多普勒外测速度阻尼方法抑制振荡误 振荡误差的效果。 差时取:陀螺常值漂移取0.003(°)/h,陀螺随机漂 通过以上方法可以在没有外部辅助信息的时 移取0.003()/h;加速度计常值漂移取5×10-g0, 候,实现对振荡误差的抑制。但是这种方法,在获得 加速度计随机漂移取5×10g。;仿真时间为12h, 高精度相移信号时存在一定的时间延迟,不能对于 仿真步长为0.01s。 误差进行完全的抑制,而且是通过自身移相进行振 分析移相抑制振荡误差方法时,取不同幅值周 荡误差的消除,并没有外部辅助信息时的系统校正 期恒定的振荡来模拟舒勒振荡误差,将原振荡误差 准确,因而只用于当系统无法获得GPS信号以及获 移动相位π后,得到移相后的振荡误差,将两者叠 得的多普勒外测速度信息不准确时。 加,得到抑制后的结果。考虑到实际应用中,在振荡 3.3GPS辅助抑制振荡误差 误差测量信号的获取以及移相处理时,存在延迟,因 在众多的外部辅助信息中,GPS信号无疑是最 而实际得到的结果并非理想情况,这里考虑加入 准确的一个,它具有误差小而恒定、不随时间发散、 5%的延迟,得到实际仿真结果。 准确度高等特点。因而成为应用十分广泛的位置校 分析GPS辅助抑制振荡误差方法时,利用在黑 准辅助信息,但是由于无人潜艇特殊的工作环境,在 龙江省哈尔滨市二龙山水库的试验数据,通过容积 水下无线电信号不能传播很远的限制,只有在水面 卡尔曼滤波方法,将捷联惯导系统与GPS辅助信息 以下几十米的范围内才可以应用GPS来辅助校准 融合。 振荡误差。利用GPS辅助信号抑制振荡误差的原 4.2仿真结果 理如图3所示。 文中所引入模型切换抑制振荡误差的方法可以 有效抑制舒勒振荡、傅科振荡、地球周期振荡等振荡 捷联惯导元器件 误差反馈 误差对于捷联惯导系统应用在无人潜艇上时,不断 比力 输出 捷联惯导 惯导 位置、速度 累积误差对于系统的影响。 角速度 解算 姿态 干导航 4.2.1差分多普勒辅助抑制振荡误差仿真分析 位置 容积 速度 卡尔曼 鑫 通过仿真结果图4~6可以看出,差分多普勒外 测速度阻尼网络可以有效抑制舒勒振荡误差对系统 GPS 大气延迟 最小二 位置 的影响。在无阻尼情况下,舒勒振荡十分明显,为周 接收机「改正等 乘解算 速度 期为84.4min的振荡,而且误差不断累积。而在外 图3GPS辅助抑制振荡误差原理图 阻尼情况下,系统的姿态误差和速度误差基本上都 Fig.3 Principle diagram of GPS assisted method to 稳定在0值附近。 suppress oscillation error
从方程(10)可以看出,振荡信号可以通过一个 相位相差 π 的幅值相等的信号进行抑制。 因此,舒 勒振荡信号以及地球周期振荡信号也可以通过相位 相差为 π 的幅值相等的信号将其抑制。 通过研究可知,陀螺漂移是捷联惯导系统误差 的主要来源,这种误差会激励舒勒振荡。 综合整理上式可得: T = 2π R g0 = 84.4 min (15) 式(15) 说明舒勒振荡是一个周期为 84.4 min 的周期振荡,根据前面分析得到的结果,利用一个相 位相差为 π 的幅值相等正余弦信号与舒勒振荡信 号融合,可以对舒勒振荡进行抑制。 由于振荡误差主要有陀螺仪以漂移以及加速度 计漂移形成,并且受经纬度等诸多因素的影响。 朱 行宜[16]设计了一种高精度相移信号发生器精度高 且价格低廉,可有效解决相移信号的产生问题,通过 防水密封等处理后,用在无人潜艇上。 将监测到的 振荡信号输入高精度相移信号发生器,设置相移为 π 后,得到的输出信号与原测量信号中和达到抑制 振荡误差的效果。 通过以上方法可以在没有外部辅助信息的时 候,实现对振荡误差的抑制。 但是这种方法,在获得 高精度相移信号时存在一定的时间延迟,不能对于 误差进行完全的抑制,而且是通过自身移相进行振 荡误差的消除,并没有外部辅助信息时的系统校正 准确,因而只用于当系统无法获得 GPS 信号以及获 得的多普勒外测速度信息不准确时。 3.3 GPS 辅助抑制振荡误差 在众多的外部辅助信息中,GPS 信号无疑是最 准确的一个,它具有误差小而恒定、不随时间发散、 准确度高等特点。 因而成为应用十分广泛的位置校 准辅助信息,但是由于无人潜艇特殊的工作环境,在 水下无线电信号不能传播很远的限制,只有在水面 以下几十米的范围内才可以应用 GPS 来辅助校准 振荡误差。 利用 GPS 辅助信号抑制振荡误差的原 理如图 3 所示。 图 3 GPS 辅助抑制振荡误差原理图 Fig.3 Principle diagram of GPS assisted method to suppress oscillation error 这里针对无人潜艇捷联惯导系统的非线性特 性,通过容积卡尔曼滤波(CKF),对捷联惯导系统测 得的 信 息 与 外 部 接 收 的 GPS 信 号 信 息 进 行 融 合[17] 。 容积卡尔曼滤波器的输入是惯导解算得到 的速度、位置和 GPS 解算得到的速度、位置,解算出 来的导航参数误差参数通过容积卡尔曼滤波器反馈 并修正捷联惯导直接计算出来的导航结果,容积卡 尔曼滤波器还将解算得到的加速度计、陀螺仪常值 零偏反馈并修正捷联惯导的原始输出,实现对振荡 误差的在线抑制[18] 。 由于 GPS 信号稳定且准确,所组合输出得到的 信息与系统实际运动的情况一致,所存在的微小误 差就是 GPS 系统的误差。 GPS 辅助抑制振荡误差 的方法是抑制振荡误差效果最好的一种方法,但是 由于 GPS 信号在水下只能传播较短距离,因而只有 在无人潜艇靠近水面时可以使用。 4 仿真分析 4.1 仿真条件 分析差分多普勒外测速度阻尼方法抑制振荡误 差时取:陀螺常值漂移取 0.003(°) / h ,陀螺随机漂 移取 0.003(°) / h ;加速度计常值漂移取 5 × 10 -5 g0 , 加速度计随机漂移取 5 × 10 -5 g0 ;仿真时间为 12 h , 仿真步长为 0.01 s 。 分析移相抑制振荡误差方法时,取不同幅值周 期恒定的振荡来模拟舒勒振荡误差,将原振荡误差 移动相位 π 后,得到移相后的振荡误差,将两者叠 加,得到抑制后的结果。 考虑到实际应用中,在振荡 误差测量信号的获取以及移相处理时,存在延迟,因 而实际得到的结果并非理想情况,这里考虑加入 5%的延迟,得到实际仿真结果。 分析 GPS 辅助抑制振荡误差方法时,利用在黑 龙江省哈尔滨市二龙山水库的试验数据,通过容积 卡尔曼滤波方法,将捷联惯导系统与 GPS 辅助信息 融合。 4.2 仿真结果 文中所引入模型切换抑制振荡误差的方法可以 有效抑制舒勒振荡、傅科振荡、地球周期振荡等振荡 误差对于捷联惯导系统应用在无人潜艇上时,不断 累积误差对于系统的影响。 4.2.1 差分多普勒辅助抑制振荡误差仿真分析 通过仿真结果图 4~6 可以看出,差分多普勒外 测速度阻尼网络可以有效抑制舒勒振荡误差对系统 的影响。 在无阻尼情况下,舒勒振荡十分明显,为周 期为 84.4 min 的振荡,而且误差不断累积。 而在外 阻尼情况下,系统的姿态误差和速度误差基本上都 稳定在 0 值附近。 ·254· 智 能 系 统 学 报 第 12 卷
第2期 王奎民,等:摸型切换抑制振荡误差在无人潜艇导航中的应用 .255. 4.2.2移相抑制振荡误差仿真分析 0.2 --…无阻尼 一外阻尼 用不同振幅的周期振荡来模拟舒勒振荡,振荡 -0.2 周期为84.4min,考虑实际情况中的抑制延迟,这里 0 2 4 6 8 10 12 加入5%的延迟。通过仿真试验验证移相抑制振荡 误差结果如图7。 0.2 无阻尼 —外阻尼 0 AAAA 振荡误差 多和后振荡误差 02 0 4 6 81012 0.5 理想抑制 0.3 实际抵制 0.1 -…无阻尼 一外阻尼 01 -0.3 4 681012 100200300400500600 时间h 图7移相抑制振荡速度误差仿真曲线 图4无阻尼与外阻尼情况下姿态误差曲线 Fig.7 Velocity error curve of suppress oscillation error Fig.4 Attitude error curve under non damping and ex- by moving phase ternal damping 将振动误差移相后叠加到原来的系统上,可以 0.6 得到理想的移相抑制振荡误差结果,即一条稳定在 -·无阻尼 一外阻尼 0.4 零值的直线。然而,实际应用中,由于振荡信号的测 0.2 0 量以及移相的处理需要一些时间,移相后叠加到的 -0.2 曲线已经不是原来的曲线。实际结果如仿真图所 0 4 6 8 10 12 示,虽然大幅减小了原来的振荡误差,但还会存在围 绕零值的小幅震荡。从以上分析可以看出,移相抑 0.4 无阻尼 外阻尼 制振荡误差的方法虽有较短时间的延迟,但仍可以 0.2 达到抑制振荡误差的效果。 -0.2 4.2.3GPS辅助抑制振荡误差试验分析 -0.4 0 2 4 6 8 10 12 GPS辅助抑制振荡误差试验的试验数据来自于 时间h (127.41E,45.73N)进行的无人潜艇环形航路湖试 图5无阻尼与外阻尼情况下速度误差曲线 试验。环形航路试验中无人潜艇在 Fig.5 Velocity error curve under non damping and ex- 600m×600m区域内沿六边形航行,实际轨迹中无 ternal damping 人潜艇航行的起点是(0,0),终点为(-75.96, 187.6)。试验结果如图8所示。 1 -无阻尼 一外阻尼 10 -1L 0 4 6 12 0 0 0.5 1.01.5 2.0 2.53.0×10 步数 =…无阻尼 一外阻尼 E 10 -0 0 6 1012 -10H 0 0.5 1.01.52.0 2.53.0*10 步数 4 -=…无阻尼 一外阻尼 图8GPS辅助抑制振荡误差时位置误差曲线图 -0L Fig.8 Position error curve under GPS assisted suppres 0 2 7 8 10 12 sion of oscillation errors 时间h 通过仿真结果图可以看出,GPS辅助抑制振荡 图6无阻尼与外阻尼情况下位置误差曲线 Fig.6 Position error curve under non damping and ex 误差效果最好,与实际航线基本吻合。误差基本稳 ternal damping 定在零值附近。对无人潜艇在海中的航行不会产生 很大影响
图 4 无阻尼与外阻尼情况下姿态误差曲线 Fig.4 Attitude error curve under non damping and ex⁃ ternal damping 图 5 无阻尼与外阻尼情况下速度误差曲线 Fig.5 Velocity error curve under non damping and ex⁃ ternal damping 图 6 无阻尼与外阻尼情况下位置误差曲线 Fig.6 Position error curve under non damping and ex⁃ ternal damping 4.2.2 移相抑制振荡误差仿真分析 用不同振幅的周期振荡来模拟舒勒振荡,振荡 周期为 84.4 min,考虑实际情况中的抑制延迟,这里 加入 5%的延迟。 通过仿真试验验证移相抑制振荡 误差结果如图 7。 图 7 移相抑制振荡速度误差仿真曲线 Fig.7 Velocity error curve of suppress oscillation error by moving phase 将振动误差移相后叠加到原来的系统上,可以 得到理想的移相抑制振荡误差结果,即一条稳定在 零值的直线。 然而,实际应用中,由于振荡信号的测 量以及移相的处理需要一些时间,移相后叠加到的 曲线已经不是原来的曲线。 实际结果如仿真图所 示,虽然大幅减小了原来的振荡误差,但还会存在围 绕零值的小幅震荡。 从以上分析可以看出,移相抑 制振荡误差的方法虽有较短时间的延迟,但仍可以 达到抑制振荡误差的效果。 4.2.3 GPS 辅助抑制振荡误差试验分析 GPS 辅助抑制振荡误差试验的试验数据来自于 (127.41°E,45.73°N)进行的无人潜艇环形航路湖试 试 验[14] 。 环 形 航 路 试 验 中 无 人 潜 艇 在 600 m × 600 m区域内沿六边形航行,实际轨迹中无 人潜艇航行的起点是 ( 0, 0) ,终点为 ( - 75. 96, 187.6)。 试验结果如图 8 所示。 图 8 GPS 辅助抑制振荡误差时位置误差曲线图 Fig.8 Position error curve under GPS assisted suppres⁃ sion of oscillation errors 通过仿真结果图可以看出,GPS 辅助抑制振荡 误差效果最好,与实际航线基本吻合。 误差基本稳 定在零值附近。 对无人潜艇在海中的航行不会产生 很大影响。 第 2 期 王奎民,等:模型切换抑制振荡误差在无人潜艇导航中的应用 ·255·

.256 智能系统学报 第12卷 4.2.4模型切换抑制振荡误差分析 sis;Pattern Recognition and Basic Technologies.Singapore, 让无人潜艇从海面一直运行到距离海底30m Singapore:SPIE,2011:8350. 以内的地方,在过程中根据高度和深度的阈值信息 [4]ZHAO Lin,LI Jiushun,CHENG Jianhua,et al.A method 切换3种误差抑制方法,得到的仿真曲线如下图9 for oscillation errors restriction of SINS based on forecasted 所示。 time series[J].Sensors,2016,15(7):17433-17452 [5]GAO Xin,BIAN Hongwei,FAN Songwei.Optimal damping 0.8 一抑制前 一抑制后 algorithm design in inertial navigation system[C]//Proceed- 0.4 ings of 2013 International Conference on Mechatronic Sci- 0.2 0 ences,Electric Engineering and Computer (MEC).Sheny- -0.2 ang:EEE,2013:2946-2949. -0.4 -0.6 [6]杜亚玲,刘建业,刘瑞华,等捷联惯性航姿系统中的 超 模糊内阻尼算法研究[J].南京航空航天大学学报, 100 200300400500600 仿真时间/min 2005,37(3):274-278. DU Yaling,LIU Jianye,LIU Ruihua,et al.Fuzzy damped 图9模型切换抑制振荡误差时速度误差曲线图 algorithm in strap down attitude heading reference system Fig.9 Velocity error curve under model switching sup- [J].Journal of Nanjing university of aeronautics astro- pression of oscillation errors nautics,2005,37(3):274-278. 通过上述仿真结果图可以看出,3种适用于不 [7]严浙平,于浩森,李本银,等.基于积分滑膜的欠驱动 同高度和深度的振荡误差抑制方法都可以在其对应 UUV地形跟踪控制[J].哈尔滨工程大学学报,2016,37 适用范围内起到较好的振荡误差抑制效果,只在3 (5):701-706. 种误差抑制方法的切换过程中稍有振荡。与传统的 YAN Zheping,YU Haomiao,LI Benyin,et al.Bottom-fol- 抑制方法相比,可以达到无人潜艇全程的误差抑制 lowing control for an underwater unmanned vehicle using in- tegral sliding mode control[J].Journal of Harbin Engineer- 效果,传统的振荡误差抑制有其适用范围,在适用范 ing University,2016,37(5):701-706. 围外汇形成误差扩大甚至发散,本文提出的方法很 [8]姜璐,于运治,陈勇.舰船惯性导航系统自适应阻尼网 好地克服了这个问题。可以很好地适用于长时间在 络设计[J].电光与控制,2014,21(4):52-55 水下航行的具有特殊军事和民用任务的无人潜艇定 JIANG Lu,YU Yunzhi,CHEN Yong.Adaptive-damp- 位使用。 ing network designed for inertial navigation system of ships [J].Electronics optics &control,2014,21(4):52-55. 5结束语 [9]MA Yanhai,FANG Jiancheng,WANG Wei,et al.Decou- 针对长时间在水下工作的无人潜艇应用的捷联 pled observability analyses of error states in INS/GPS inte- 惯导系统会产生误差累积的问题,设计了一种模型切 gration[]]Journal of navigation,2014,67(3):473-494. [10]ZHENG Z C,YUE J.A novel GPS/INS loose integrated 换抑制振荡误差的方法。克服传统抑制误差方法的 navigation algorithm[J].Advanced materials research, 不足,在水下不同深度和高度选择最优的振荡误差抑 2013.823:479-484. 制方法。仿真结果表明,相对于单一振荡误差抑制方 [11]HEGRENAS O,BERGLUND E,HALLINGSTAD O.Mod- 法存在应用局限,模型切换抑制振荡误差方法可以在 el-aided inertial navigation for underwater vehicles [Cl// 海面下不同深度和高度对振荡误差进行有效抑制。 Proceedings of 2008 IEEE International Conference on Ro- 这对于有军事任务或搜寻任务的需要长时间在水下 botics and Automation.Pasadena:IEEE,2008:1069- 作业的无人潜艇而言具有重要的实际应用价值。 1076. [12]秦瑞,王顺伟,袁晓峰,等.多普勒测速仪/捷联惯导 参考文献: 组合导航技术研究[J].战术导弹技术,2006(6):68 72. [1]黄德鸣,程禄.惯性导航系统[M].北京:国防工业出版 QIN Rui,WANG Shunwei,YUAN Xiaofeng,et al.Study 社.1986:122-125. of integrated navigation of strap-down inertial navigation ai- [2]XU Bo,SUN Feng.An independent damped algorithm based ded by DVL[]]Tactical missile technology,2006(6): on SINS for ship [C]//Proceedings of 2009 International 68-72. Conference on Computer Engineering and Technology.Sin- [13]程建华,王通达,宋春雨,等.舰船捷联惯导传递对准 gapore:IEEE,2009:88-92. 的改进自适应滤波算法「J].系统工程与电子技术, [3]WANG Chao,ZHU Hai,LI Gang,et al.The mixed level 2016,38(3):638-643. damping of the single-axial rotation of INS[C]//Proceed- CHENG Jianhua,WANG Tongda,SONG Chunyu,et al. ings of SPIE,Fourth International Conference on Machine Modified adaptive Filter algorithm for shipborne SINS Vision (ICMV 2011):Computer Vision and Image Analy- transfer alignment[].Systems engineering and electron-
4.2.4 模型切换抑制振荡误差分析 让无人潜艇从海面一直运行到距离海底 30 m 以内的地方,在过程中根据高度和深度的阈值信息 切换 3 种误差抑制方法,得到的仿真曲线如下图 9 所示。 图 9 模型切换抑制振荡误差时速度误差曲线图 Fig.9 Velocity error curve under model switching sup⁃ pression of oscillation errors 通过上述仿真结果图可以看出,3 种适用于不 同高度和深度的振荡误差抑制方法都可以在其对应 适用范围内起到较好的振荡误差抑制效果,只在 3 种误差抑制方法的切换过程中稍有振荡。 与传统的 抑制方法相比,可以达到无人潜艇全程的误差抑制 效果,传统的振荡误差抑制有其适用范围,在适用范 围外汇形成误差扩大甚至发散,本文提出的方法很 好地克服了这个问题。 可以很好地适用于长时间在 水下航行的具有特殊军事和民用任务的无人潜艇定 位使用。 5 结束语 针对长时间在水下工作的无人潜艇应用的捷联 惯导系统会产生误差累积的问题,设计了一种模型切 换抑制振荡误差的方法。 克服传统抑制误差方法的 不足,在水下不同深度和高度选择最优的振荡误差抑 制方法。 仿真结果表明,相对于单一振荡误差抑制方 法存在应用局限,模型切换抑制振荡误差方法可以在 海面下不同深度和高度对振荡误差进行有效抑制。 这对于有军事任务或搜寻任务的需要长时间在水下 作业的无人潜艇而言具有重要的实际应用价值。 参考文献: [1]黄德鸣, 程禄. 惯性导航系统[M]. 北京: 国防工业出版 社, 1986: 122-125. [2]XU Bo, SUN Feng. An independent damped algorithm based on SINS for ship [ C] / / Proceedings of 2009 International Conference on Computer Engineering and Technology. Sin⁃ gapore: IEEE, 2009: 88-92. [3]WANG Chao, ZHU Hai, LI Gang, et al. The mixed level damping of the single⁃axial rotation of INS [ C] / / Proceed⁃ ings of SPIE, Fourth International Conference on Machine Vision ( ICMV 2011): Computer Vision and Image Analy⁃ sis; Pattern Recognition and Basic Technologies. Singapore, Singapore: SPIE, 2011: 8350. [4]ZHAO Lin, LI Jiushun, CHENG Jianhua, et al. A method for oscillation errors restriction of SINS based on forecasted time series[J]. Sensors, 2016, 15(7): 17433-17452. [5]GAO Xin, BIAN Hongwei, FAN Songwei. Optimal damping algorithm design in inertial navigation system[C] / / Proceed⁃ ings of 2013 International Conference on Mechatronic Sci⁃ ences, Electric Engineering and Computer (MEC). Sheny⁃ ang: IEEE, 2013: 2946-2949. [6]杜亚玲, 刘建业, 刘瑞华, 等. 捷联惯性航姿系统中的 模糊内阻尼算法研究[ J]. 南京航空航天大学学报, 2005, 37(3): 274-278. DU Yaling, LIU Jianye, LIU Ruihua, et al. Fuzzy damped algorithm in strap down attitude heading reference system [J]. Journal of Nanjing university of aeronautics & astro⁃ nautics, 2005, 37(3): 274-278. [7]严浙平,于浩淼,李本银,等. 基于积分滑膜的欠驱动 UUV 地形跟踪控制[J]. 哈尔滨工程大学学报,2016, 37 (5):701-706. YAN Zheping, YU Haomiao, LI Benyin, et al. Bottom-fol⁃ lowing control for an underwater unmanned vehicle using in⁃ tegral sliding mode control[J]. Journal of Harbin Engineer⁃ ing University, 2016, 37 (5):701-706. [8]姜璐, 于运治, 陈勇. 舰船惯性导航系统自适应阻尼网 络设计[J]. 电光与控制, 2014, 21(4): 52-55. JIANG Lu, YU Yunzhi, CHEN Yong. Adaptive⁃damp⁃ ing network designed for inertial navigation system of ships [J]. Electronics optics &control, 2014, 21(4): 52-55. [9]MA Yanhai, FANG Jiancheng, WANG Wei, et al. Decou⁃ pled observability analyses of error states in INS / GPS inte⁃ gration[J]. Journal of navigation, 2014, 67(3): 473-494. [10]ZHENG Z C, YUE J. A novel GPS / INS loose integrated navigation algorithm [ J ]. Advanced materials research, 2013, 823: 479-484. [11]HEGRENAS O, BERGLUND E, HALLINGSTAD O. Mod⁃ el⁃aided inertial navigation for underwater vehicles[ C] / / Proceedings of 2008 IEEE International Conference on Ro⁃ botics and Automation. Pasadena: IEEE, 2008: 1069 - 1076. [12]秦瑞, 王顺伟, 袁晓峰, 等. 多普勒测速仪/ 捷联惯导 组合导航技术研究[J]. 战术导弹技术, 2006(6): 68- 72. QIN Rui, WANG Shunwei, YUAN Xiaofeng, et al. Study of integrated navigation of strap⁃down inertial navigation ai⁃ ded by DVL[ J]. Tactical missile technology, 2006( 6): 68-72. [13]程建华, 王通达, 宋春雨, 等. 舰船捷联惯导传递对准 的改进自适应滤波算法[ J]. 系统工程与电子技术, 2016, 38(3): 638-643. CHENG Jianhua, WANG Tongda, SONG Chunyu, et al. Modified adaptive Filter algorithm for shipborne SINS transfer alignment [ J]. Systems engineering and electron⁃ ·256· 智 能 系 统 学 报 第 12 卷

第2期 王奎民,等:模型切换抑制振荡误差在无人潜艇导航中的应用 ·257. ics,2016,38(3):638-643. [18]刘帅.GPS/NS组合导航算法研究与实现[D].郑州: [14]王振凯,黄显林.SNS/GPS组合导航系统解析性能分 解放军信息工程大学,2012:8-28. 析[J].哈尔滨工程大学学报,2015,36(11):1488- LIU Shuai.Research and implementation of GPS/INS inte- 1493. grated navigation algorithm[D].Harbin:Harbin Engineer- WANG Z K,HUANG X L.Analytical performance analysis ing University,2012:8-28. of SINS/GPS integrated navigation[J].Journal of Harbin 作者简介: Engineering University,2015,36(11):1488-1493. [15]CHENG Jianhua,WANG Tongda,GUAN Dongxue,et al. 王奎民,男,1971年生.高级工程师.博 Polar transfer alignment of shipborne SINS with a large 士,主要研究方向水下航行器控制与仿真。 misalignment angle[J].Measurement science and technol- 0g,2016,27(2):35101. [16]朱行宜.高精度相移信号发生器[J].仪表技术,1997 (5):30-40. ZHU Xingyi.High-precision turning-phase Signal source [J].Instrumentation technology,1997(5):30-40. [17]王宏健,李村,么洪飞,等.基于高斯混合容积卡尔曼 郭占军,男,1963年,海军海洋测绘 滤波的UUV自主导航定位算法[J].仪器仪表学报, 研究所防险救生研究室高级工程师。 2015,36(2):254-261. 主要研究方向为海洋测绘、无人潜艇导 WANG Hongjian,LI Cun,YAO Hongfei,et al.Gaussian 航控制等。 mixture cubature Kalman filter based autonomous naviga tion and localization algorithm for UUV[J].Chinese jour- nal of scientific instrument,2015,36(2):254-261. 第十二届中国生物特征识别大会 2017 Chinese Conference On Biometric Recognition 中国生物特征识别大会(Chinese Conference on Biometric Recognition)是由中国人工智能学会(CAAI)主办的 国内生物特征识别领域的学术盛会。自2000年始,CCB已经在北京、杭州、西安、广州、济南、沈阳、天津和成都 等地成功举办了11届,有力促进了国内本领域的学术和技术发展。 第十二届中国生物特征识别大会(CCBR2017)将于2017年10月28-29日在深圳举行,由深圳大学计算机与 软件学院和哈尔滨工业大学(深圳)计算机科学与技术学院联合承办。本届会议将汇聚国内从事生物特征识别理 论与应用研究的广大科研工作者,并邀请国际同行,共同分享我国生物特征识别研究的最新理论和技术成果,为 大家提供精彩的学术盛宴。 征文范围包括(不局限于): 生物特征获取装置; 步态识别: 生物特征信号质量评价与增强; 其他生物特征的识别与处理: 基于生物特征的情感计算; 多模态生物识别与信息融合: 人脸检测、识别与跟踪: 生物特征数据库建设与合成: 指纹、掌纹、静脉识别: 大规模生物特征识别系统: 虹膜识别; 生物特征识别系统防伪与安全: 说话人识别: 生物特征识别系统评估及应用。 笔迹(含签名)识别: 会议网站:http:/cv.sz.edu.cn/ccbr2017/
ics, 2016, 38(3): 638-643. [14]王振凯,黄显林. SINS / GPS 组合导航系统解析性能分 析[ J]. 哈尔滨工程大学学报,2015, 36 ( 11):1488 - 1493. WANG Z K, HUANG X L. Analytical performance analysis of SINS / GPS integrated navigation[ J]. Journal of Harbin Engineering University, 2015, 36(11): 1488-1493. [15]CHENG Jianhua, WANG Tongda, GUAN Dongxue, et al. Polar transfer alignment of shipborne SINS with a large misalignment angle[J]. Measurement science and technol⁃ ogy, 2016, 27(2): 35101. [16]朱行宜. 高精度相移信号发生器[ J]. 仪表技术, 1997 (5): 30-40. ZHU Xingyi. High⁃precision turning⁃phase Signal source [J]. Instrumentation technology, 1997(5): 30-40. [17]王宏健, 李村, 么洪飞, 等. 基于高斯混合容积卡尔曼 滤波的 UUV 自主导航定位算法[ J]. 仪器仪表学报, 2015, 36(2): 254-261. WANG Hongjian, LI Cun, YAO Hongfei, et al. Gaussian mixture cubature Kalman filter based autonomous naviga⁃ tion and localization algorithm for UUV[ J]. Chinese jour⁃ nal of scientific instrument, 2015, 36(2): 254-261. [18]刘帅. GPS / INS 组合导航算法研究与实现[D]. 郑州: 解放军信息工程大学, 2012: 8-28. LIU Shuai. Research and implementation of GPS / INS inte⁃ grated navigation algorithm[D]. Harbin: Harbin Engineer⁃ ing University, 2012: 8-28. 作者简介: 王奎民,男,1971 年生,高级工程师,博 士,主要研究方向水下航行器控制与仿真。 郭占军,男,1963 年,海军海洋测绘 研究所防险救生研究室高级工程师。 主要研究方向为海洋测绘、无人潜艇导 航控制等。 第十二届中国生物特征识别大会 2017 Chinese Conference On Biometric Recognition 中国生物特征识别大会(Chinese Conference on Biometric Recognition)是由中国人工智能学会(CAAI)主办的 国内生物特征识别领域的学术盛会。 自 2000 年始,CCBR 已经在北京、杭州、西安、广州、济南、沈阳、天津和成都 等地成功举办了 11 届,有力促进了国内本领域的学术和技术发展。 第十二届中国生物特征识别大会(CCBR2017)将于 2017 年 10 月 28-29 日在深圳举行,由深圳大学计算机与 软件学院和哈尔滨工业大学(深圳)计算机科学与技术学院联合承办。 本届会议将汇聚国内从事生物特征识别理 论与应用研究的广大科研工作者,并邀请国际同行,共同分享我国生物特征识别研究的最新理论和技术成果,为 大家提供精彩的学术盛宴。 征文范围包括(不局限于): 生物特征获取装置; 生物特征信号质量评价与增强; 基于生物特征的情感计算; 人脸检测、识别与跟踪; 指纹、掌纹、静脉识别; 虹膜识别; 说话人识别; 笔迹(含签名)识别; 步态识别; 其他生物特征的识别与处理; 多模态生物识别与信息融合; 生物特征数据库建设与合成; 大规模生物特征识别系统; 生物特征识别系统防伪与安全; 生物特征识别系统评估及应用。 会议网站:http: / / cv.szu.edu.cn / ccbr2017 / 第 2 期 王奎民,等:模型切换抑制振荡误差在无人潜艇导航中的应用 ·257·