
北京化2大学 第一章聚合物加工流变学基础理论简介 Beijing Uaiversity of Chemical Technolog 第五节 聚合物流变学基础方程的初步应用 一、3 引言 1、目的 描述流场中流体物性及运动参数的数值及分布状态; 对流体的流动变形进行定量表征,预测产品的质量; 确定合理的流场流道的尺寸和配套的加工工艺条件
第一章 聚合物加工流变学基础理论简介 聚合物加工流变学基础理论简介 第五节 聚合物流变学基础方程的初步应用 聚合物流变学基础方程的初步应用 描述流场中流体物性及运动参数的数值及分布状态; 描述流场中流体物性及运动参数的数值及分布状态; 对流体的流动变形进行定量表征,预测产品的质量; 对流体的流动变形进行定量表征,预测产品的质量; 确定合理的流场流道的尺寸和配套的加工工艺条件。 确定合理的流场流道的尺寸和配套的加工工艺条件。 1、目的 一、引言

第一章聚合物加工流变学基础理论简介震 北京化二大学 第五节 聚合物流变学基础方程的初步应用 一、引言 2、分析问题思路 建立物理模型(提出假设条件) 模型求解 结果讨论
第一章 聚合物加工流变学基础理论简介 聚合物加工流变学基础理论简介 第五节 聚合物流变学基础方程的初步应用 聚合物流变学基础方程的初步应用 建立物理模型(提出假设条件) 建立物理模型(提出假设条件) 模型求解 结果讨论 2、分析问题思路 、分析问题思路 一、引言

第五节 聚合物流变学基础方程的初步应 北京化二大学 Beijing Uaiversity of Chemical Technology 一、引言 2、分析问题思路 (1)建立物理模型(提出假设条件) 分析实际加工过程:决定取舍因素 袭 流体运动基础方程十本构方程 体现加工过程速度场、 力场、温度场特征及材料对外界条件响应的易于求解方程
(1)建立物理模型(提出假设条件) )建立物理模型(提出假设条件) 分析实际加工过程:决定取舍因素 流体运动基础方程+本构方程 体现加工过程速度场、 力场、温度场特征及材料对外界条件响应的易于求解方程 。 形成 第五节 聚合物流变学基础方程的初步应用 聚合物流变学基础方程的初步应用 一、引言 2、分析问题思路 、分析问题思路

第五节 聚合物流变学基础方程的初步应用 北京化二大学 一、 引言 2、分析问题思路 (2)模型求解 用数学方法及场的边界条件求解数学模型。 (3)对求解数学模型进行讨论 提出对加工的指导意义,并进行修正和评价 3、流体的流动类型 拖曳流、压力流、拖曳十压力流
(2)模型求解 用数学方法及场的边界条件求解数学模型。 用数学方法及场的边界条件求解数学模型。 (3)对求解数学模型进行讨论 )对求解数学模型进行讨论 提出对加工的指导意义,并 提出对加工的指导意义,并进行修正和评价 3、流体的流动类型 、流体的流动类型 拖曳流、压力流、拖曳+压力流 拖曳流、压力流、拖曳+压力流 第五节 聚合物流变学基础方程的初步应用 聚合物流变学基础方程的初步应用 一、引言 2、分析问题思路 、分析问题思路
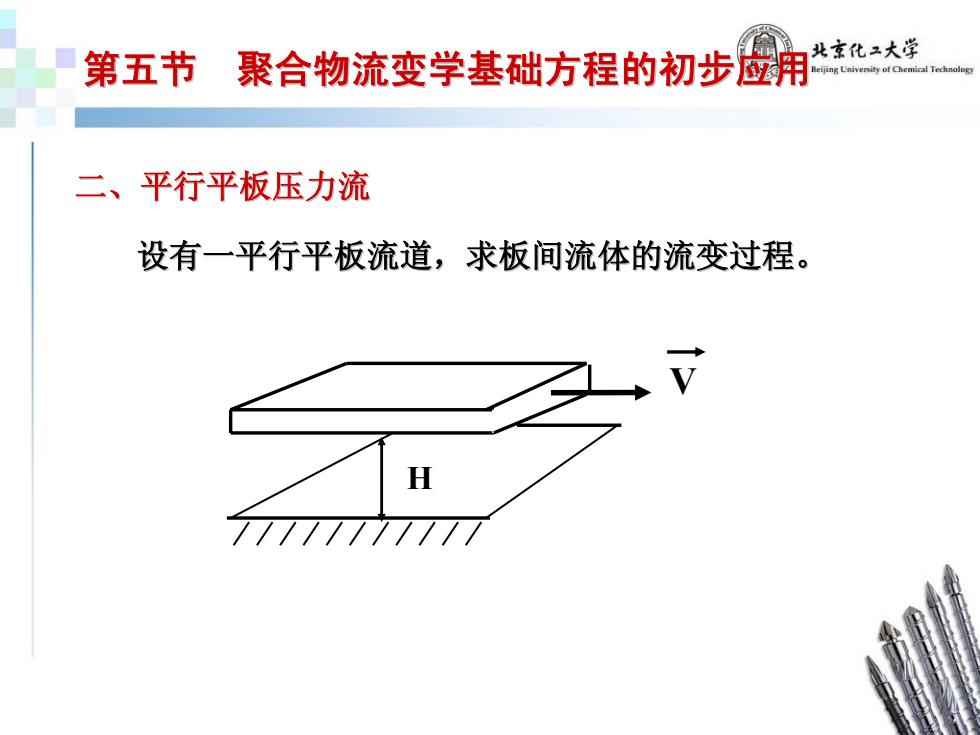
第五节 聚合物流变学基础方程的初步应 北京化二大学 Beijing Uaiversity of Chemical Technology 二、平行平板压力流 设有一平行平板流道,求板间流体的流变过程。 H
设有一平行平板流道,求板间流体的流变过程。 设有一平行平板流道,求板间流体的流变过程。 V H 第五节 聚合物流变学基础方程的初步应用 聚合物流变学基础方程的初步应用 二、平行平板压力流 二、平行平板压力流
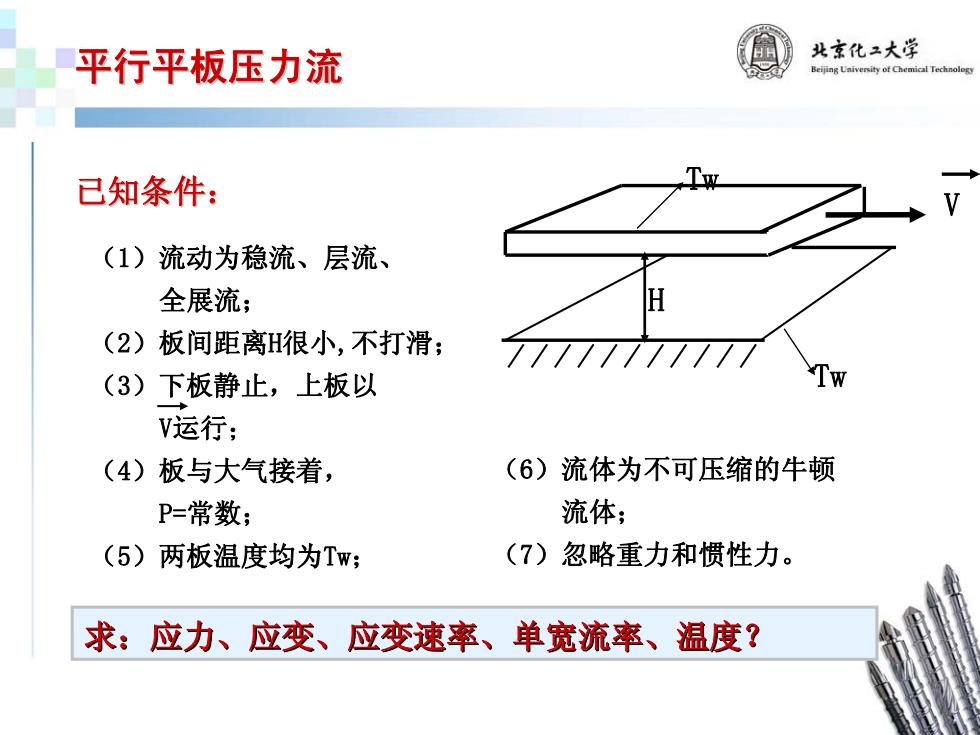
平行平板压力流 北京化2大学 已知条件: (1)流动为稳流、层流、 全展流; (2)板间距离H很小,不打滑; (3)下板静止,上板以 Tw V运行; (4)板与大气接着, (6)流体为不可压缩的牛顿 P=常数; 流体; (5)两板温度均为Tw; (7)忽略重力和惯性力。 求:应力、应变、应变速率、单宽流率、温度?
已知条件: (6)流体为不可压缩的牛顿 流体; (7)忽略重力和惯性力。 V H (1)流动为稳流、层流、 全展流; (2)板间距离H很小,不打滑; (3)下板静止,上板以 V运行; (4)板与大气接着, P=常数; (5)两板温度均为Tw; Tw Tw 平行平板压力流 平行平板压力流 求:应力、应变、应变速率、单宽流率、温度? 求:应力、应变、应变速率、单宽流率、温度?
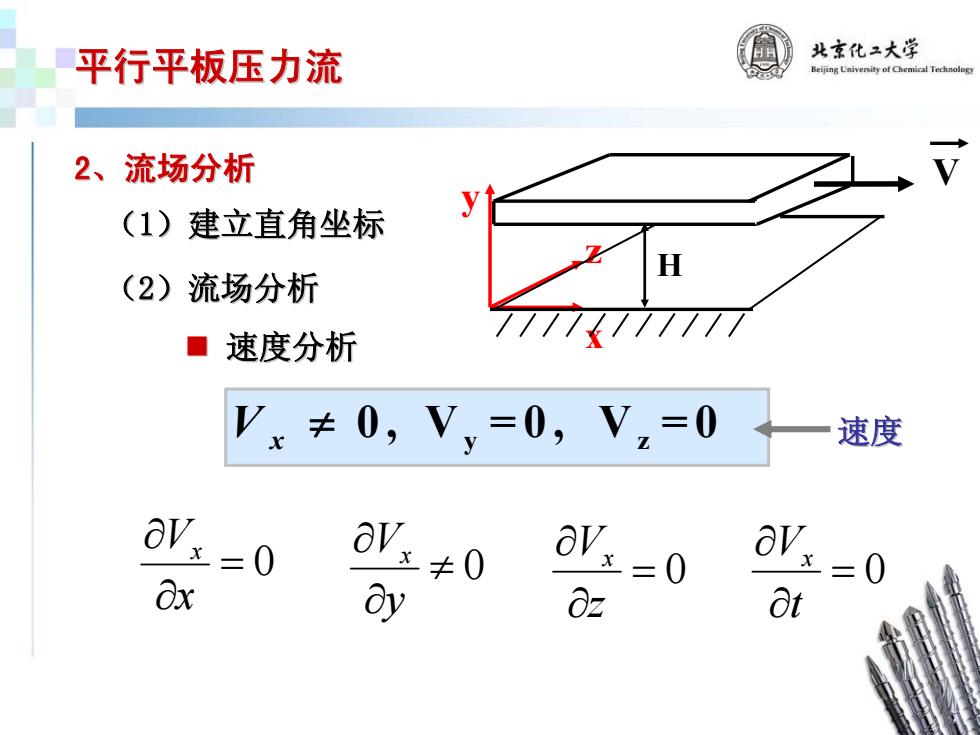
平行平板压力流 北京化2大学 Beijing Uaiversity of Chemical Technology 2、流场分析 (1)建立直角坐标 (2)流场分析 ■速度分析 Vx≠0,Vy=0,Vz=0 速度 V:=0 aV+0 OV:-0 Ox oVs-0 dy 0z Ot
2、流场分析 (1)建立直角坐标 )建立直角坐标 (2)流场分析 速度分析 = 0 ∂ ∂ x Vx ≠ 0 ∂ ∂ y Vx = 0 ∂ ∂ z Vx = 0 ∂ ∂ t Vx y z 0, V =0, V =0 V x ≠ 速度 x y z V H 平行平板压力流 平行平板压力流

平行平板压力流 北京化二大学 应变速率 y 0 oV: 0 dy []= 0 ay y 0 0
[ ] ⎡ ∂ ⎤ ⎢ ⎥ ∂ ⎢ ⎥ ⎢ ∂ ⎥ ⎢ ⎥ ∂ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ x · x 0 0 y γ= 0 0 y 0 00 V V [ ] xy yx τ τ τ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 0 0 = 00 0 00 应变速率 [ ] ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ∂ ∂ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ∂ ∂ = • zyzx z yx y yz x xzxy V V V V V V V VV V VV V V V z x z y z y x y y z x x y x z 2 2 2 γ 平行平板压力流 平行平板压力流

平行平板压力流 北京化二大学 Beijing Uaiversity of Chemical Technology 温度变化 aT =0 ot ≠0 aT =0 10 8x dy 0z 8t
温度变化 0 T x ∂ = ∂ 0 Ty ∂ ≠ ∂ 0 Tz ∂ = ∂ 0 Tt ∂ = ∂ 平行平板压力流 平行平板压力流

平行平板压力流 北京化2大学 Beijing University of Chemical Technology 3、建立方程 (1)X方向的运动方程 +装,器+粉 X方向的运动方程表达式 0yx二0 --(1) ay
3、建立方程 (1)X方向的运动方程 方向的运动方程 x xx yx zx x z x y x x x g) zyx ( x P ) z V V y V V x V V t V ( ρ+ ∂ τ∂ + ∂ τ∂ + ∂ τ∂ + ∂ ∂ −= ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ ρ ∂ ∂ τy x = 0 y X方向的运动方程表达式 方向的运动方程表达式 ---(1) 平行平板压力流 平行平板压力流