
第四节:流变学的基础方程 北京化二大学 Beijing University of Chemical Technology 一、连续性方程(板书推导) 股=-( =-p) p+a(pw,(p)+(pr)-0 Ot Ex ∂z
第四节:流变学的基础方程 第四节:流变学的基础方程 一、连续性方程(板书推导) 一、连续性方程(板书推导) ( ) V t ρ ρ ∂ = −∇ • ∂ G ( ) ( ) ( ) 0 x y z V V V tx y z ∂ρ ∂ ρ ∂ ρ ∂ ρ +++= ∂∂ ∂ ∂ ( ) D V Dt ρ =− ∇• ρ G

第四节:流变学的基础方程 北京化二大学 Beijing Lniversity of Chemical Technology 一、连续性方程 物理意义: 单位时间单位体积内质量的变化=单位时间沿X、Y、 Z三个方向上单位面积净流入质量之和。 或者说:净流出与质量变化之和为零
第四节:流变学的基础方程 第四节:流变学的基础方程 一、连续性方程 一、连续性方程 物理意义: 单位时间单位体积内质量的变化 单位时间单位体积内质量的变化 =单位时间沿 X 、 Y 、 Z三个方向上单位面积净流入质量之和。 三个方向上单位面积净流入质量之和。 或者说:净流出与质量变化之和为零。 净流出与质量变化之和为零

第四节:流变学的基础方程 北京化二大学 Beijing University of Chemical Technology 二、运动方程(动量方程)—板书推导 DP P Dt =-VP+V[z]+pg 物理意义: 动量变化(惯性力)=净压力+净应力+重力 流体在X、Y、Z方向上单位体积动量的变化 =流体在X、Y、Z方向上压力变化、应力变化和重力之和
第四节:流变学的基础方程 第四节:流变学的基础方程 二、运动方程(动量方程) 二、运动方程(动量方程)——板书推导 [ ] DV P g Dt ρ = −∇ + ∇ • + τ ρ G G 物理意义: 动量变化(惯性力) 动量变化(惯性力)= 净压力 + 净应力 + 重力 流体在 X 、 Y 、 Z方向上单位体积动量的变化 方向上单位体积动量的变化 =流体在 X 、 Y 、 Z方向上压力变化、应力变化和重力之和 方向上压力变化、应力变化和重力之和

第四节:流变学的基础方程 北京化二大学 Beijing Lniversity of Chemical Technology 二、运动方程(动量方程) OV+V av. x+V av x+V aP 0下必十 T 8t y :0z Bx Ox dy Oz +pgx av. av + ar, (g+ y 0t型 :0z ax Oy Oz OV:V av OV:+V: a业: 0t地 8t a Bzax y Oz +pg:
第四节:流变学的基础方程 第四节:流变学的基础方程 二、运动方程(动量方程) 二、运动方程(动量方程) x x xx xx yx zx xyz x y y yy xy yy zy xyz y z z zz xz yz xyz VVVV P VVV g t x y z x xyz VVVV P VVV g t x y z y xyz VVVV P VVV t x y z zx τ τ τ ρ ρ τττ ρ ρ τ τ ρ ⎛ ⎞ ∂∂∂∂ ∂ ∂ ⎛ ⎞ ∂ ∂ ⎜ ⎟ + + + =− + + + + ⎜ ⎟ ⎝ ⎠ ∂ ∂ ∂ ∂ ∂ ∂∂∂ ⎝ ⎠ ⎛ ⎞ ∂ ∂ ∂ ∂ ∂∂∂ ∂ ⎛ ⎞ ⎜ ⎟ + + + =− + + + + ⎜ ⎟ ∂ ∂ ∂ ∂ ∂ ∂∂∂ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ ∂∂∂∂ ∂ ∂ ∂ ⎜ ⎟ + + + =− + + ⎝ ⎠ ∂ ∂ ∂ ∂ ∂∂ zz z g y z τ ρ ⎛ ⎞ ∂ ⎜ ⎟ + + ∂ ∂ ⎝ ⎠
第四节:流变学的基础方程 此京化二大学 Beijing University of Chemical Technology 主、能量方程 能量守恒定律: 1、推导思路 E一单位质量流体的能量 ∂(pE) dxdydz 8t dz dVs (1)流体流动净带入的能量 (2)热传导净带入的能量(温差) dx dy (3)应力做功 (4)重力做功
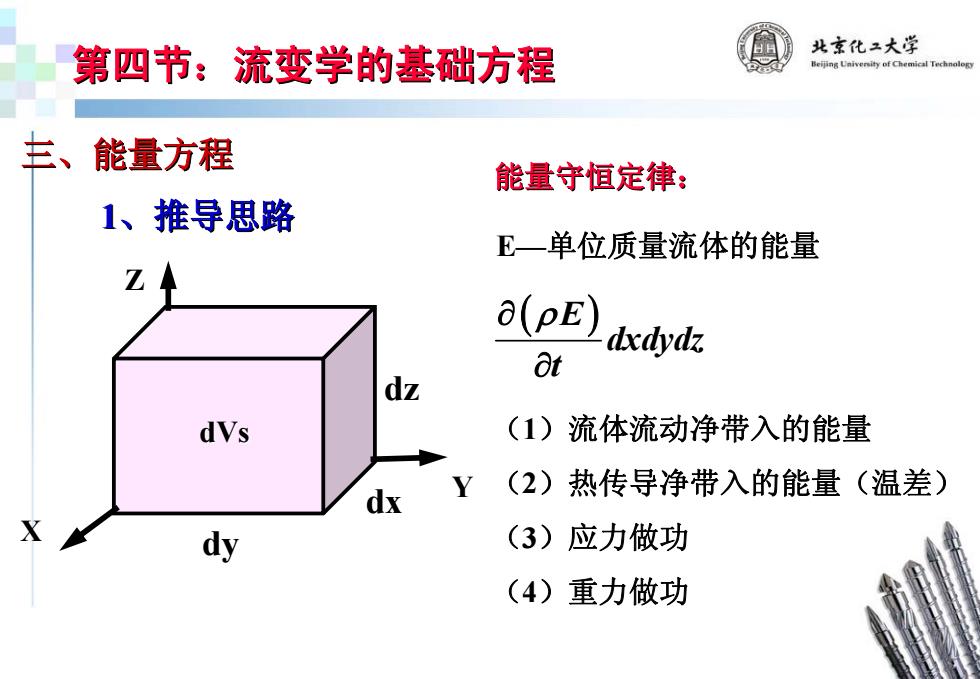
第四节:流变学的基础方程 第四节:流变学的基础方程 三、能量方程 1、推导思路 E —单位质量流体的能量 单位质量流体的能量 ( E ) dxdydz t ∂ ρ ∂ ( 1)流体流动净带入的能量 )流体流动净带入的能量 ( 2)热传导净带入的能量(温差) )热传导净带入的能量(温差) ( 3)应力做功 ( 4)重力做功 能量守恒定律: 能量守恒定律: X Y Z dx dy dz dVs

第四节:流变学的基础方程 北京化二大学 Beijing Lniversity of Chemical Technology 三、能量方程 1、推导思路 (1)流体流动净带入的能量 (2)热传导净带入的能量(温差) (3)应力做功 (4)重力做功
第四节:流变学的基础方程 第四节:流变学的基础方程 三、能量方程 1、推导思路 ( 1 )流体流动净带入的能量 流体流动净带入的能量 ( 2 )热传导净带入的能量(温差) 热传导净带入的能量(温差) ( 3 )应力做功 ( 4 )重力做功

第四节:流变学的基础方程 北京化二大学 Beijing University of Chemical Technology (1)流体流动净带入的能量 Epy dyd Epy,dxdz dz Ep Epy,+ d Vs x dx dy EpV,dxdy
X Y Z dx dy dz dVs (1)流体流动净带入的能量 )流体流动净带入的能量 第四节:流变学的基础方程 第四节:流变学的基础方程 x x E V E V dx dydz x ρ ρ ⎛ ⎞ ∂ + ⎜ ⎟ ⎝ ⎠ ∂ E V dx ρ ydz EρV dxdz y y y E V E V dy dxdz yρ ρ ⎛ ⎞ ∂ ⎜ ⎟ + ∂ ⎝ ⎠ EρV dxdy z z z E V E V dz dxdy z ρ ρ ⎛ ⎞ ∂ + ⎜ ⎟ ⎝ ⎠ ∂

第四节:流变学的基础方程 北京化二大学 Beijing Lniversity of Chemical Technology (2)热传导的能量 ot 9 dydz j=-k On |dxdy 4,dxdz dz 04s dx dydz dx y 9.dxdy
X Y Z dx dy dz dVs (2)热传导的能量 )热传导的能量 第四节:流变学的基础方程 第四节:流变学的基础方程 x x q q dx dydz x ⎛ ⎞ ∂ + ⎜ ⎟ ⎝ ⎠ ∂ x q dydz y q dxdz y y q q dy dxdz y ⎛ ⎞ ∂ ⎜ ⎟ + ∂ ⎝ ⎠ z q dxdy z z dz z q q dxdy q dz dxdy z + ⎛ ⎞ ∂ = + ⎜ ⎟ ⎝ ⎠ ∂ T q k n ∂ = − ∂ G G

第四节:流变学的基础方程 北京化2大学 Beijing University of Chemical Technology (3)应力做功 : (V:)os= + V ot dx ax :dx + Ox
第四节:流变学的基础方程 第四节:流变学的基础方程 ( 3)应力做功 X Y Z dx dy dz dVs ( ) xy y xy y xy y x dx V V dx V dx x x τ τ τ + ⎛ ⎞ ∂ ∂ ⎛ ⎞ =+ + ⎜ ⎟⎜ ⎟ ∂ ∂ ⎝ ⎠⎝ ⎠ ( ) xx x xx x x dx xx x V V dx V dx x x τ τ τ + ⎛ ⎞ ∂ ∂ ⎛ ⎞ =+ + ⎜ ⎟⎜ ⎟ ⎝ ⎠ ∂ ∂ ⎝ ⎠ τ xx x V ( ) xz z xz z xz z x dx V V dx V dx x x τ τ τ + ⎛ ⎞ ∂ ∂ ⎛ ⎞ =+ + ⎜ ⎟⎜ ⎟ ⎝ ⎠ ∂ ∂ ⎝ ⎠ τ xy y V τ xz z V

第四节:流变学的基础方程 北京化二大学 Beijing Lniversity of Chemical Technology (4)重力做功 pg● 2-7(5p)-vi+v-+s7
第四节:流变学的基础方程 第四节:流变学的基础方程 ( 4)重力做功 ρ g • V G G ( ) ( ) [ ] E E V qV g V t ρ ρ τ ρ ∂ = −∇ • − ∇ • + ∇ • • + • ∂ G G G G G