
第一章:流变学基础理论知识简介 北京化二大学 Beijing Uaiversity of Chemical Technology 一个模 型:连续介质模型 两种描述方法: 拉格朗日法、欧拉法 三个基本概念:应力、应变、应变速率 三个基础方程:连续性方程、运动方程、能量方程 两个本构方程:牛顿流体本构方程 幂律流体幂律方程 基础方程的初步应用
第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介 一个模 型:连续介质模型 型:连续介质模型 两种描述方法:拉格朗日法、欧拉法 两种描述方法:拉格朗日法、欧拉法 三个基本概念:应力、应变、应变速率 三个基本概念:应力、应变、应变速率 三个基础方程:连续性方程、运动方程、能量方程 三个基础方程:连续性方程、运动方程、能量方程 两个本构方程:牛顿流体本构方程 两个本构方程:牛顿流体本构方程 幂律流体幂律方程 幂律流体幂律方程 基础方程的初步应用 基础方程的初步应用

北京化二大学 第一章:流变学基础理论知识简介 1、一个模型:连续介质模型 不考虑微观分子结构,把流体视为由无数多个充 满流体所在空间、相互间无任何间隙的质点所组 成,相邻质点宏观物理量的变化是连续的。 ●B=B(x,y,z) ●B(x,y,Z)是连续可微的
1、一个模型:连续介质模型 、一个模型:连续介质模型 不考虑微观分子结构,把流体视为由无数多个充 不考虑微观分子结构,把流体视为由无数多个充 满流体所在空间、相互间无任何间隙的质点所组 满流体所在空间、相互间无任何间隙的质点所组 成,相邻质点宏观物理量的变化是连续的。 成,相邻质点宏观物理量的变化是连续的。 z B=B(x, y, z x, y, z) z B(x, y, z x, y, z)是连续可微的 )是连续可微的 第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介

北京化二大学 第一章:流变学基础理论知识简介 Beijing Uaiversity of Chemical Technology 2、两种描述方法 拉格朗日法:着眼点在质点 欧拉法:着眼点在空间点(无位移函数) 两种描述方法的质点导数 DB aB V 6B Dt *x V,oy +.V B
2、两种描述方法 、两种描述方法 拉格朗日法:着眼点在质点 拉格朗日法:着眼点在质点 欧拉法:着眼点在空间点(无位移函数) 欧拉法:着眼点在空间点(无位移函数) 两种描述方法的质点导数 两种描述方法的质点导数 第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介 xyz DB B B B B VVV Dt t x y z V B t ∂ ∂∂∂ ⎛ ⎞ =+ + + ⎜ ⎟ ∂ ⎝ ⎠ ∂∂∂ ⎛ ⎞ ∂ = + •∇ ⎜ ⎟ ⎝ ⎠ ∂ G
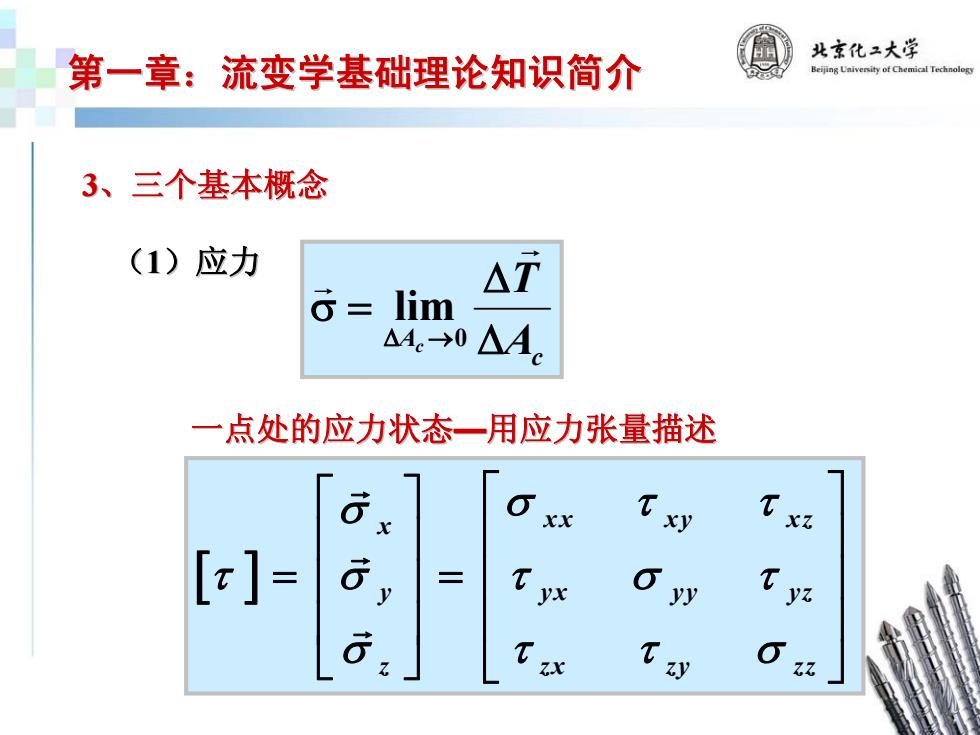
第一章:流变学基础理论知识简介 北京化2大学 3、三个基本概念 (1)应力 △T 6= lim △4e→0 △A 一点处的应力状态一用应力张量描述 []= T 6
第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介 3、三个基本概念 、三个基本概念 ( 1)应力 c A A T c Δ Δ =σ →Δ G G 0 lim 一点处的应力状态 一点处的应力状态 —用应力张量描述 用应力张量描述 [ ] xx x y x z x y y x yy y z z zx zy zz σ σ τ τ τ σ τστ σ τ τσ ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ G G G
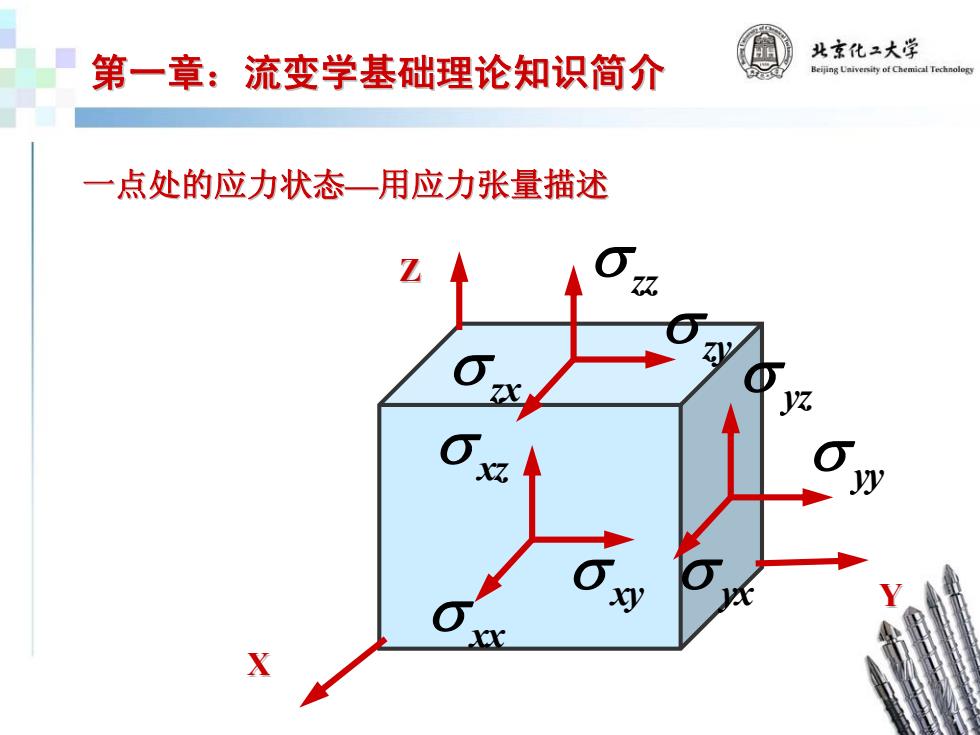
北京化2大学 第一章:流变学基础理论知识简介 Beijing Uaiversity of Chemical Technology 一点处的应力状态一用应力张量描述
第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介 X Y Z σ xx σ xy σ xz σ yy σ yx σ yz σ zz σ zy σ zx 一点处的应力状态 一点处的应力状态—用应力张量描述 用应力张量描述
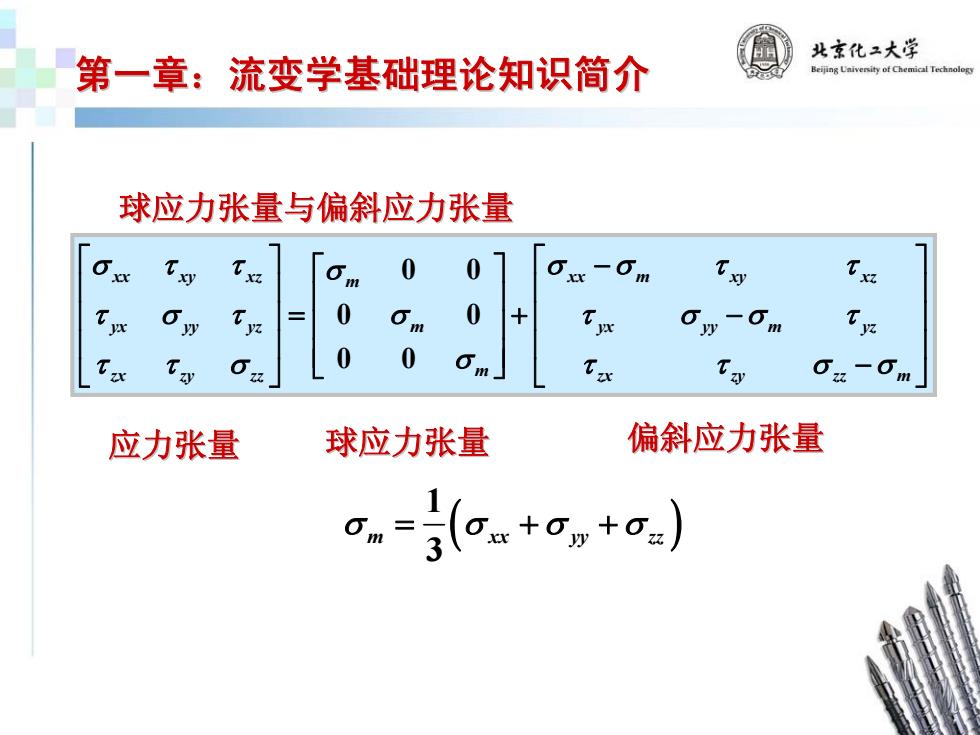
北京化二大学 第一章:流变学基础理论知识简介 球应力张量与偏斜应力张量 m 0 0 一m y 6 0 0 0 一m 0 0 m 人 0x-0m 应力张量 球应力张量 偏斜应力张量 o=(o。+on+a)
球应力张量与偏斜应力张量 球应力张量与偏斜应力张量 0 0 0 0 0 0 xx xy xz m xx m xy xz yx yy yz m yx yy m yz zx zy zz m zx zy zz m σττ σ σσ τ τ τ στ σ τ σσ τ τ τ σ σ τ τ σσ ⎡⎤ ⎡ − ⎤ ⎡ ⎤ ⎢⎥ ⎢ ⎥ ⎢ ⎥ ⎢⎥ ⎢ = +− ⎥ ⎢ ⎥ ⎢⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − ⎣⎦ ⎣ ⎦ ( ) 1 3 σ m x = ++ σσσ x yy zz 应力张量 球应力张量 偏斜应力张量 第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介
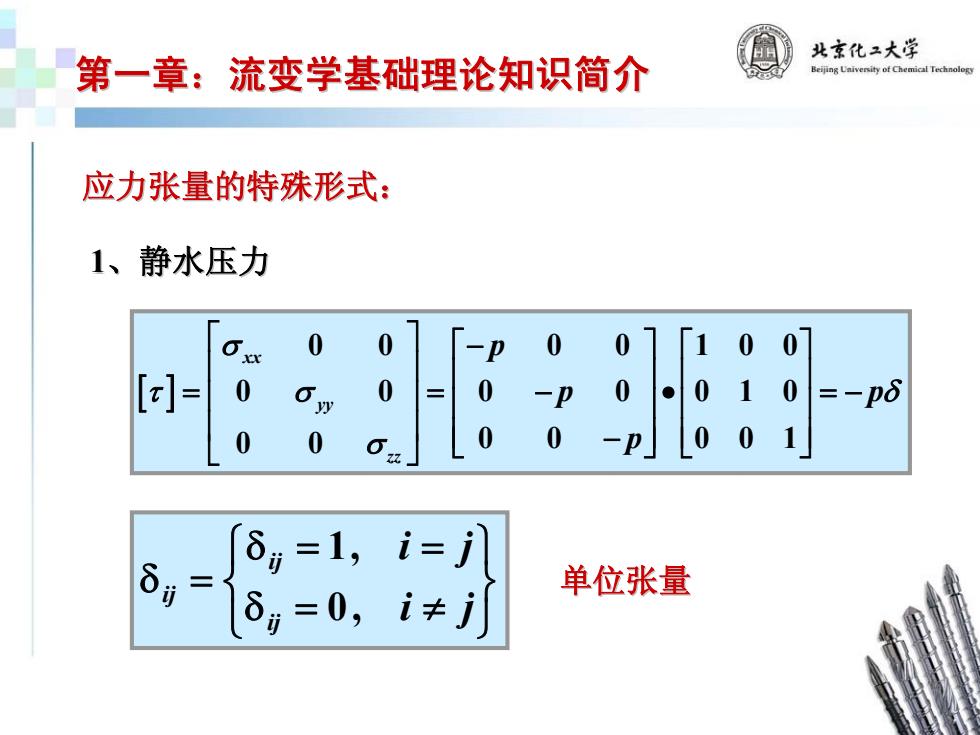
北京化2大学 第一章:流变学基础理论知识简介 Beijing Uaiversity of Chemical Technology 应力张量的特殊形式: 1、静水压力 6 0 0 -P 0 1 0 [= 0 0 y 0 0 ● 0 10 =-p6 0 0 0 0 -P 0 01 δj δ,=1,i=j 单位张量 δ=0,i≠j
第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介 应力张量的特殊形式: 应力张量的特殊形式: [ ] 0 0 0 0 100 0 0 0 0 010 0 0 0 0 001 xx yy zz p p p p σ τ σ δ σ ⎡ ⎤ ⎡ ⎤⎡ ⎤ − ⎢ ⎥ ⎢ ⎥⎢ ⎥ = =− • = ⎢ ⎥ − ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎣ ⎦⎣ ⎦ ⎢ ⎥⎢ ⎥ − ⎣ ⎦ 1、静水压力 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ≠=δ ==δ =δ ji ji ijij ij ,0,1 单位张量
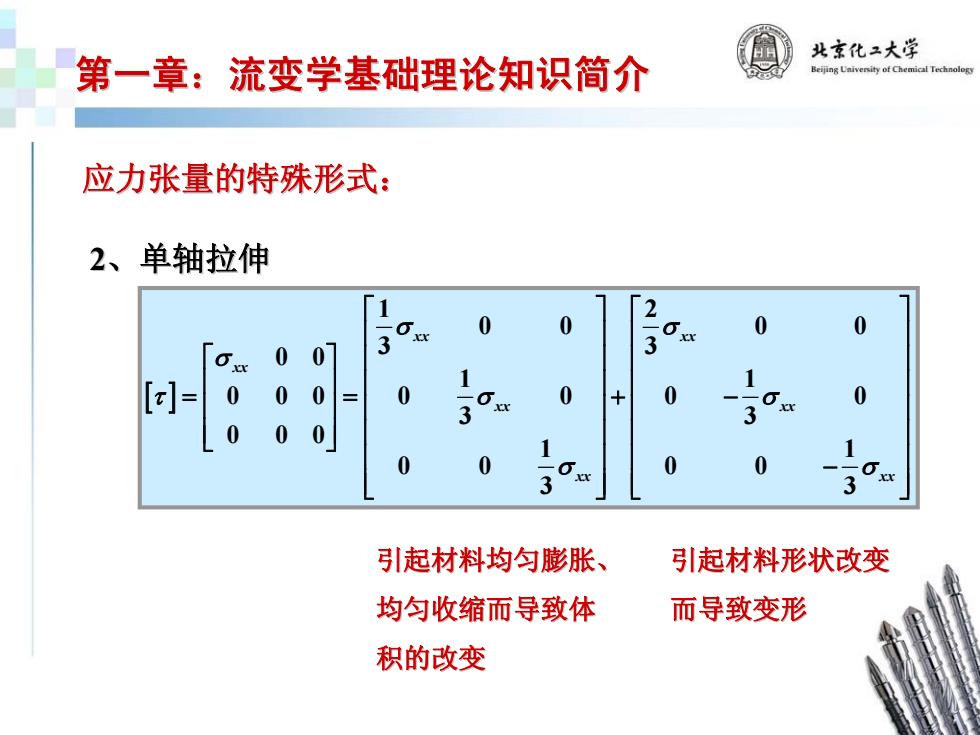
北京化二大学 第一章:流变学基础理论知识简介 应力张量的特殊形式: 2、单轴拉伸 0 0 07 3 2-3 0 0 0 []= 0 0 0 0 0 0 0 3 3 0 0 0 0 0 0 3 3 引起材料均匀膨胀、 引起材料形状改变 均匀收缩而导致体 而导致变形 积的改变
第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介 应力张量的特殊形式: 应力张量的特殊形式: 2、单轴拉伸 [ ] 1 2 00 0 0 3 3 0 0 1 1 0 00 0 0 0 0 3 3 0 00 1 1 00 0 0 3 3 xx xx xx xx xx xx xx σ σ σ τ σσ σ σ ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = = +− ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎢ − ⎥ ⎢⎣ ⎥ ⎢ ⎦ ⎣ ⎥⎦ 引起材料均匀膨胀、 均匀收缩而导致体 积的改变 引起材料形状改变 而导致变形
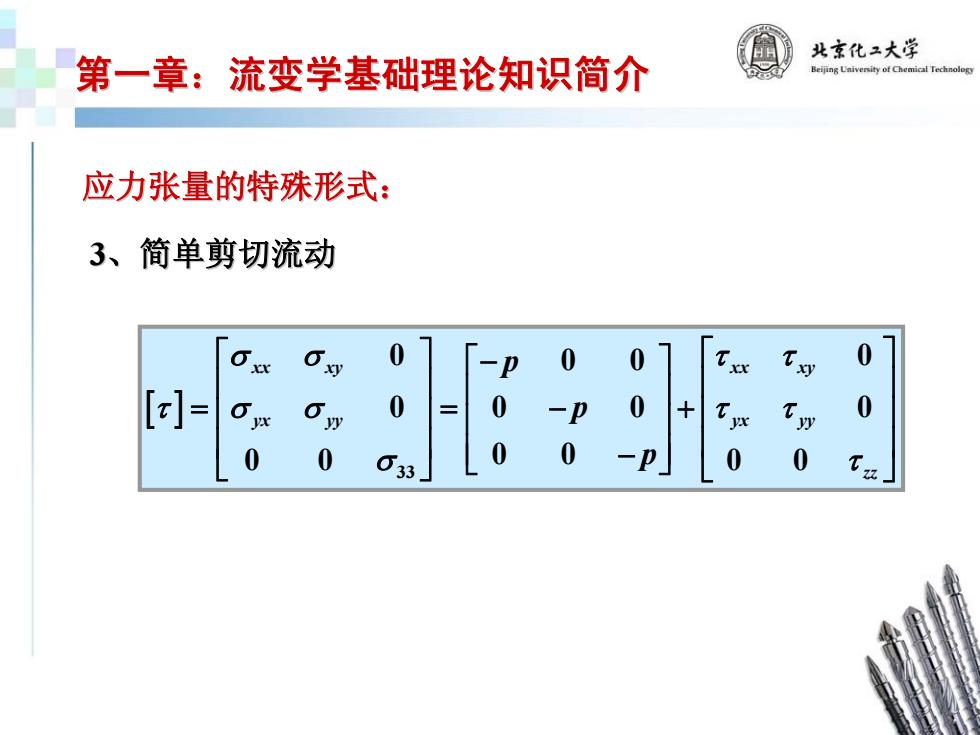
北京化二大学 第一章:流变学基础理论知识简介 Beijing Uaiversity of Chemical Technology 应力张量的特殊形式: 3、简单剪切流动 0 -P 0 Tx [= 0 0 -P 0 + 0 0 0 33 0 0 一p 0 0
[ ] 33 0 0 0 0 00 0 0 0 0 0 0 0 0 xx xy xx xy yx yy yx yy zz p p p σ σ τ τ τ σσ τ τ σ τ ⎡ ⎤ − ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = =− + ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − ⎣ ⎦ ⎣ ⎦ 第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介 应力张量的特殊形式: 应力张量的特殊形式: 3、简单剪切流动 、简单剪切流动

第一章:流变学基础理论知识简介 北京化2大学 3、三个基本概念 (2)应变 一点处的应变状态一用应变张量描述 us 1-2 u. Ox: []= ax 8y ay Oz 1 ou. us 1 Ou: u 2 ax Oz 2 ay Bz
第一章:流变学基础理论知识简介 第一章:流变学基础理论知识简介 3、三个基本概念 、三个基本概念 ( 2)应变 一点处的应变状态 一点处的应变状态 —用应变张量描述 用应变张量描述 [ ] 1 1 2 2 1 1 2 2 1 1 2 2 xx x y z z y yy x z zz z x y uu u u u x yx x x u uu u u xy y zy uu u u u xz yz z ε ⎡ ∂∂ ∂ ⎛ ⎞ ∂ ⎛ ⎞ ∂ ⎤ ⎢ ⎜ ⎟ + + ⎜ ⎟⎥ ∂ ∂∂ ∂ ∂ ⎢ ⎝ ⎠ ⎝ ⎠⎥ ⎢ ⎥ ⎛⎞ ⎛⎞ ∂ ∂∂ ∂ ∂ ⎢ ⎥ = + ⎜⎟ ⎜⎟ + ⎢ ∂∂ ∂ ∂∂ ⎥ ⎝⎠ ⎝⎠ ⎢ ⎥ ⎢ ⎛ ⎞ ∂∂ ∂ ∂ ⎛ ⎞ ∂ ⎥ ⎢ ⎜ ⎟ + + ⎜ ⎟ ⎥ ⎝ ⎠ ∂∂ ∂∂ ∂ ⎣ ⎝ ⎠ ⎦