
无视及分饭化学 结构和元素周期表
无机及分析化学 原子结构和元素周期表

基本内容和重点要求 以3.1原子核外电子的运动状态 3.2原子核外电子的排布和元素周期律 3.3元素基本性质的周期性 重点要求掌握四个量子数对核外电子运动状态的描 述熟悉s,p,d原子轨道和电子云的形状和伸展方向;掌握 周期系内各元素原子的核外电子层结构的特征,电子排 布规律
基本内容和重点要求 重点要求掌握四个量子数对核外电子运动状态的描 述熟悉s,p,d原子轨道和电子云的形状和伸展方向;掌握 周期系内各元素原子的核外电子层结构的特征,电子排 布规律 3.1 原子核外电子的运动状态 3.2 原子核外电子的排布和元素周期律 3.3 元素基本性质的周期性

3.1核外电子的运动状态 一、玻尔的原子结构理论 二、电子的玻粒二象性 三、玻函数与原子轨道 四、概率密度和电子云图形 五、四个量子数
3.1 核外电子的运动状态 一、 玻尔的原子结构理论 二、 电子的玻粒二象性 三、 玻函数与原子轨道 四、 概率密度和电子云图形 五、 四个量子数

3.1.1玻尔的原子结构理论 连续光谱 (自然界)
连续光谱 (自然界) 3.1.1 玻尔的原子结构理论

连续光谱(实验室) *45668
连续光谱(实验室)
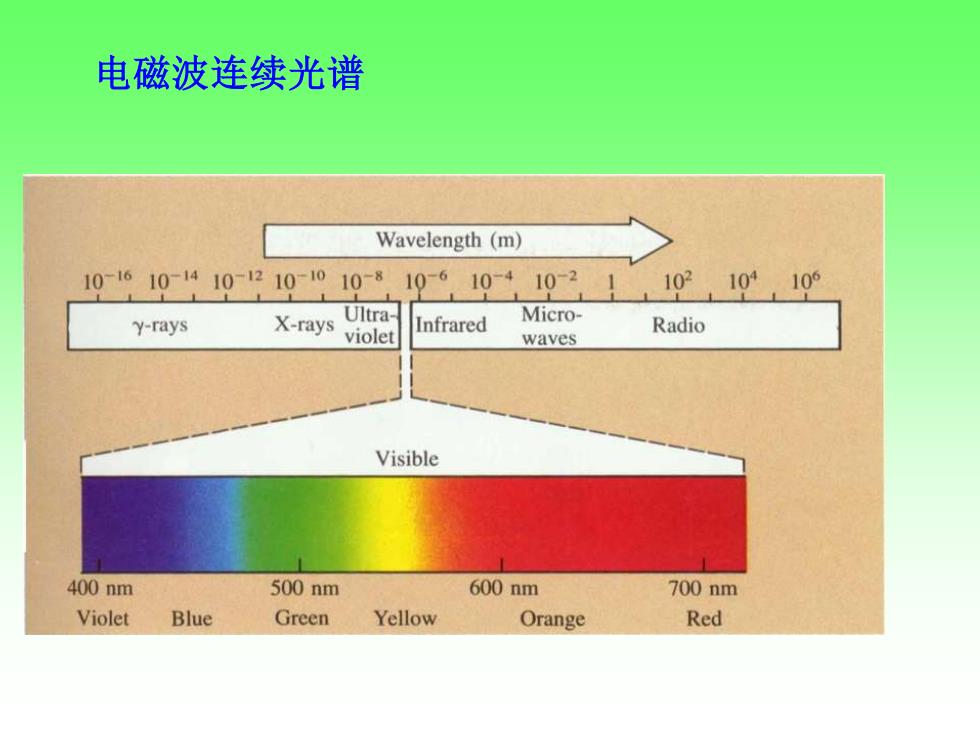
电磁波连续光谱 Wavelength(m) 10610410-210010-8 10-610-4 103 10210,10 Ultra Micro- y-rays X-rays Infrared violet Radio waves Visible 400nm 500nm 600nm 700nm Violet Blue Green Yellow Orange Red
电磁波连续光谱
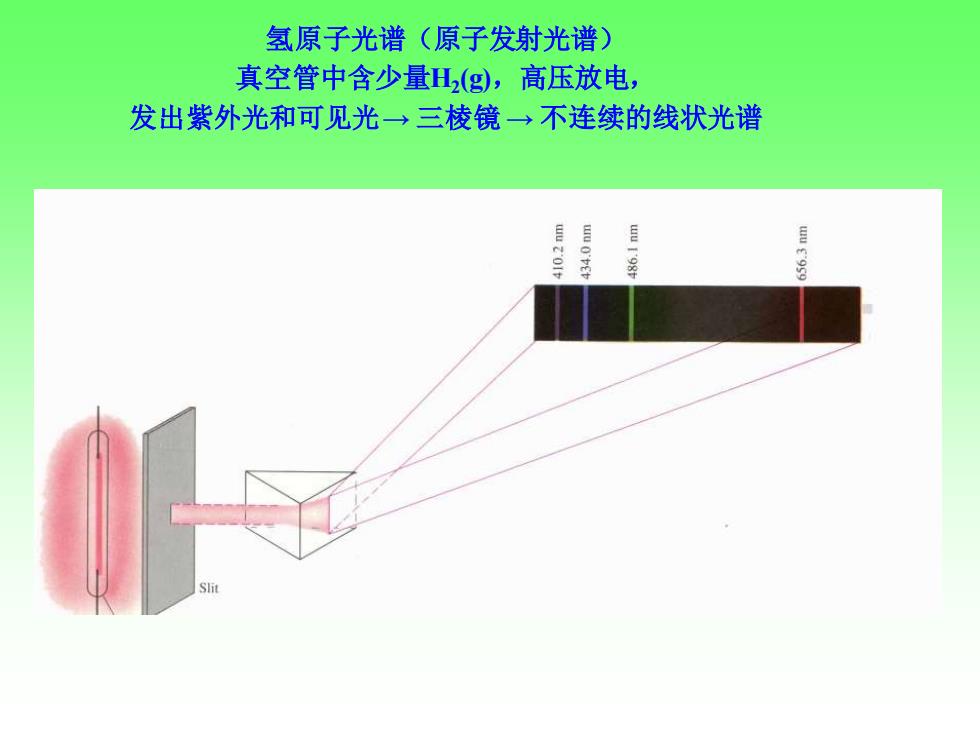
氢原子光谱(原子发射光谱) 真空管中含少量H(g,高压放电, 发出紫外光和可见光→三棱镜-→不连续的线状光谱
氢原子光谱(原子发射光谱) 真空管中含少量H2 (g),高压放电, 发出紫外光和可见光→ 三棱镜 → 不连续的线状光谱

一、玻尔的原子结构埋论 1913年丹麦物理学家(N.Bohhr)在氢原子光谱和普朗克(M.Planck) 量子理论的基础上提出了如下假设: 原子中的电子只能沿着某些特定的、以原子核为中心、半径和能量 都确定的轨道上运动,这些轨道的能量状态不随时间而改变,称为 稳定轨道(或定态轨道)。 >在一定轨道中运动的电子具有一定的能量,处在稳定轨道中运动的电 子,既不吸收能量,也不发射能量。电子只有从一个轨道跃迁到另一 轨道时,才有能量的吸收和放出。在离核越近的轨道中,电子被原子 核束缚越牢,其能量越低;在离核越远的轨道上,其能量越高。轨道 的这些不同的能量状态,称为能级。轨道不同,能级也不同。在正常 状态下,电子尽可能处于离核较近、能量较低的轨道上运动,这时原 子所处的状态称为基态,其余的称为激发态。 >电子从一个定态轨道跳到另一个定态轨道,在这过程中放出或吸收 能量,其频率与两个定态轨道之间的能量差有关。 返回
1913年丹麦物理学家(N.Bohhr)在氢原子光谱和普朗克(M.Planck) 量子理论的基础上提出了如下假设: ➢原子中的电子只能沿着某些特定的、以原子核为中心、半径和能量 都确定的轨道上运动,这些轨道的能量状态不随时间而改变,称为 稳定轨道(或定态轨道)。 ➢在一定轨道中运动的电子具有一定的能量,处在稳定轨道中运动的电 子,既不吸收能量,也不发射能量。电子只有从一个轨道跃迁到另一 轨道时,才有能量的吸收和放出。在离核越近的轨道中,电子被原子 核束缚越牢,其能量越低;在离核越远的轨道上,其能量越高。轨道 的这些不同的能量状态,称为能级。轨道不同,能级也不同。在正常 状态下,电子尽可能处于离核较近、能量较低的轨道上运动,这时原 子所处的状态称为基态,其余的称为激发态。 ➢电子从一个定态轨道跳到另一个定态轨道,在这过程中放出或吸收 能量,其频率与两个定态轨道之间的能量差有关。 一、玻尔的原子结构理论 返回

3.1.2电子的玻粒二象性 1924年,法国年轻的物理学家L.de Broglie (1892一1987)指出,对于光的本质的研究,人们长期以来 注重其波动性而忽略其粒子性;与其相反,对于实物粒子的 研究中,人们过分重视其粒子性而忽略了其波动性。 光的干涉、衍射等现象说明光具有波动性;而光电效 应、光的发射、吸收又说明光具有粒子性。因此光具有波 动和粒子两重性,称为光的波粒二象性。 返回
3.1.2 电子的玻粒二象性 1924 年,法国年轻的物理学家 L. de Broglie ( 1892 — 1987 )指出,对于光的本质的研究,人们长期以来 注重其波动性而忽略其粒子性;与其相反,对于实物粒子的 研究中,人们过分重视其粒子性而忽略了其波动性。 光的干涉、衍射等现象说明光具有波动性;而光电效 应、光的发射、吸收又说明光具有粒子性。因此光具有波 动和粒子两重性,称为光的波粒二象性。 返回

光的波粒二象性启发了法国物理学家德布罗意(de Broglie), 1924年,他提出了一个大胆的假设:认为微观粒子都具有波粒 二象性;也就是说,微观微粒除具有粒子性外,还具有波的性 质,这种波称为德布罗意波或物质波。1927年,德布罗意的假 设经电子衍射实验得到了完全证实。美国物理学家戴维逊 (C.J.Davisson)和革末(L.H.Ge rmer)进行了电子衍射实验,当 将一束高速电子流通过镍晶体(作为光栅)而射到荧光屏上时,结 果得到了和光衍射现象相似的一系列明暗交替的衍射环纹,这 种现象称为电子衍射。衍射是一切波动的共同特征,由此充分 证明了高速运动的电子流,也具有波粒二象性。除光子、电子 外,其他微观粒子如:质子、中子等也具有波粒二象性
光的波粒二象性启发了法国物理学家德布罗意(de Broglie), 1924年,他提出了一个大胆的假设:认为微观粒子都具有波粒 二象性;也就是说,微观微粒除具有粒子性外,还具有波的性 质,这种波称为德布罗意波或物质波。1927年,德布罗意的假 设经电子衍射实验得到了完全证实。美国物理学家戴维逊 (C.J.Davisson)和革末(L.H.Ge rmer) 进行了电子衍射实验,当 将一束高速电子流通过镍晶体(作为光栅)而射到荧光屏上时,结 果得到了和光衍射现象相似的一系列明暗交替的衍射环纹,这 种现象称为电子衍射。衍射是一切波动的共同特征,由此充分 证明了高速运动的电子流,也具有波粒二象性。除光子、电子 外,其他微观粒子如:质子、中子等也具有波粒二象性