
弯曲液面的力平衡条件 回顾:热力学力平衡条件: 体系各相压强相等 p1=p2=p3=p4=. 考虑了表面效应后,这一关系是否还成立
弯曲液面的力平衡条件 回顾:热力学力平衡条件: 体系各相压强相等 p1=p2=p3=p4=. 考虑了表面效应后,这一关系是否还成立

弯曲液面的力平衡条件 如图所示两相平衡体系, a相 T 在等温、等容情况下达到平衡 *6相 的判据为:(dF)ry=0 To A 6相 dF dF+dFB+dF dFa=-SodTa-pdva dFB=-SBdTB-pfdy dF=-SdTo-pdv+ydA (dv=0)
弯曲液面的力平衡条件 如图所示两相平衡体系, 在等温、等容情况下达到平衡 的判据为: , ( ) 0 T V dF = dF dF dF dF = + + dF S dT p dV dF S dT p dV dF S dT p dV dA = − − = − − = − − + ( 0) dV =

弯曲液面的力平衡条件 考虑到等温、等容条件,则: dTa=dTB=dTo=0. dv=dva+dvB=0 .dF=-pdva+pdya+ydA=O dA p-p= 此即考虑表面效应后两相力平衡条件
弯曲液面的力平衡条件 考虑到等温、等容条件,则: dT dT dT dV dV dV 0, 0 = = = = + = 0 dF p dV p dV dA = − + + = dA p p dV − = 此即考虑表面效应后两相力平衡条件
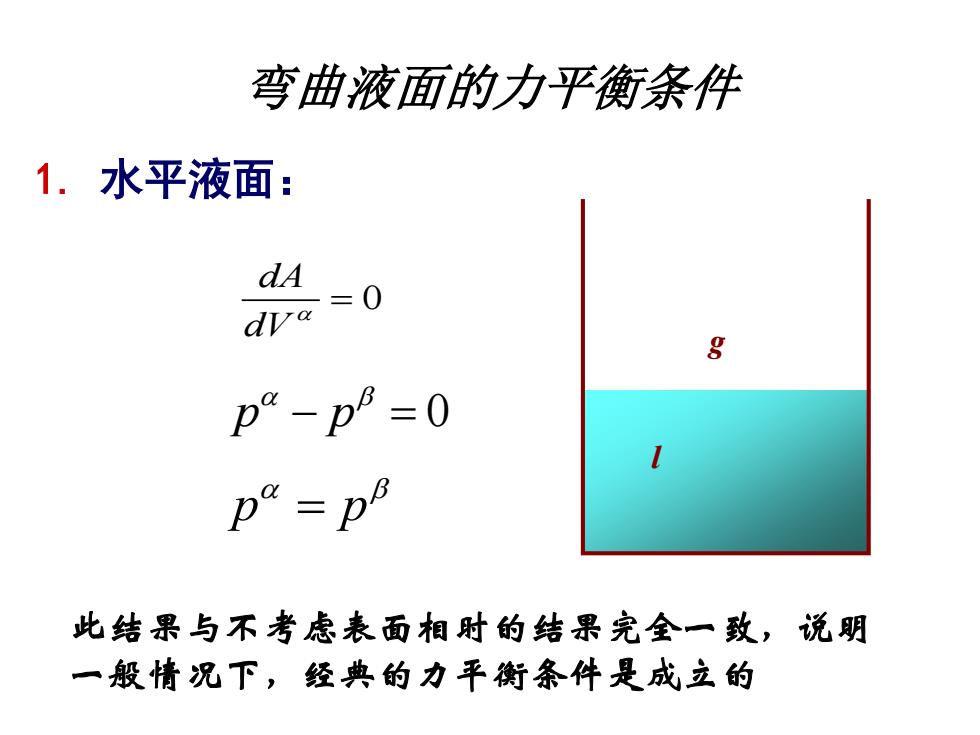
弯曲液面的力平衡条件 1.水平液面: -0 dA g p-p=0 p=p 此结果与不考虑表面相时的结果完全一致,说明 一般情况下,经典的力平衡条件是成立的
弯曲液面的力平衡条件 1. 水平液面: 0 dA dV = p p 0 − = p p = 此结果与不考虑表面相时的结果完全一致,说明 一般情况下,经典的力平衡条件是成立的 g l
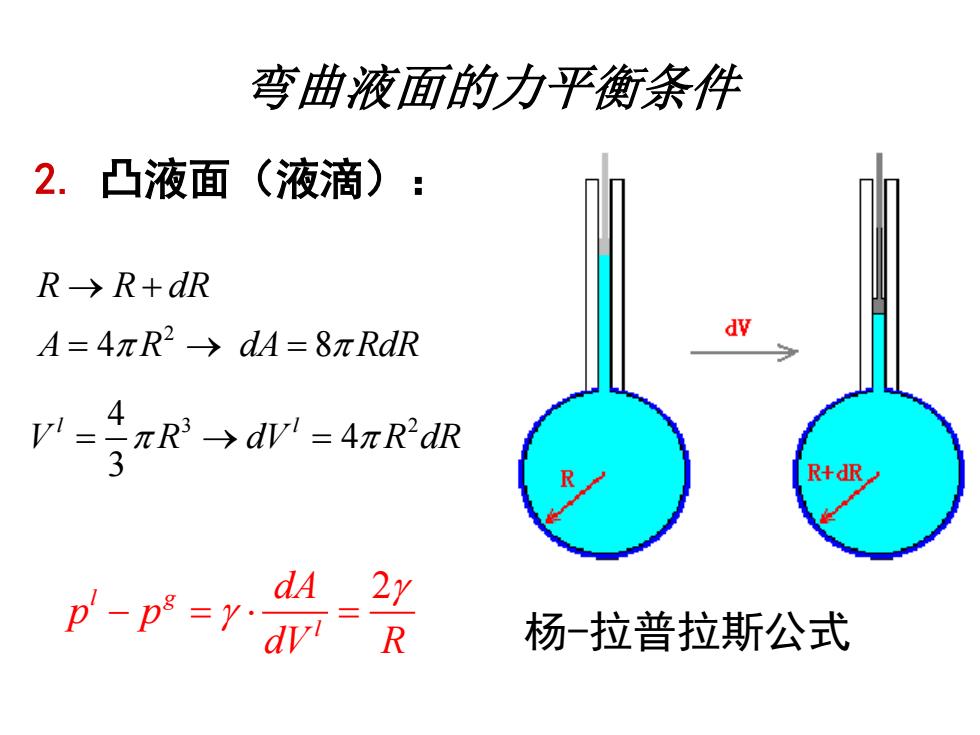
弯曲液面的力平衡条件 2.凸液面(液滴): R→R+dR A=4πR2→dA=8mRdR r-音R→=4标Rd讼 R+dR dA p-p*=Y.dvi 2y R 杨-拉普拉斯公式
弯曲液面的力平衡条件 2. 凸液面(液滴): 2 4 8 R R dR A R dA RdR → + = → = 4 3 2 4 3 l l V R dV R dR = → = l g 2 l dA p p dV R − = = 杨-拉普拉斯公式
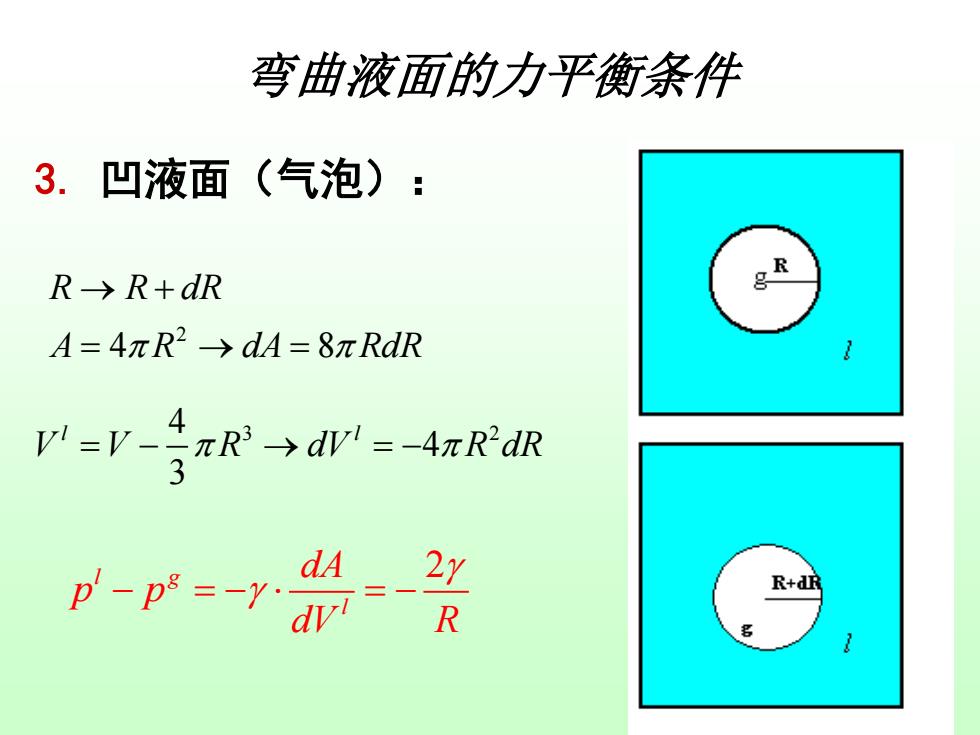
弯曲液面的力平衡条件 3.凹液面(气泡): R→R+dR A=4πR2→dA=8πRdR yR→dP=-4πR脉 dA p-p*=-y.dvi 2y R+dR R
弯曲液面的力平衡条件 3. 凹液面(气泡): 2 4 8 R R dR A R dA RdR → + = → = 4 3 2 4 3 l l V V R dV R dR = − → = − l g 2 l dA p p dV R − = − = −
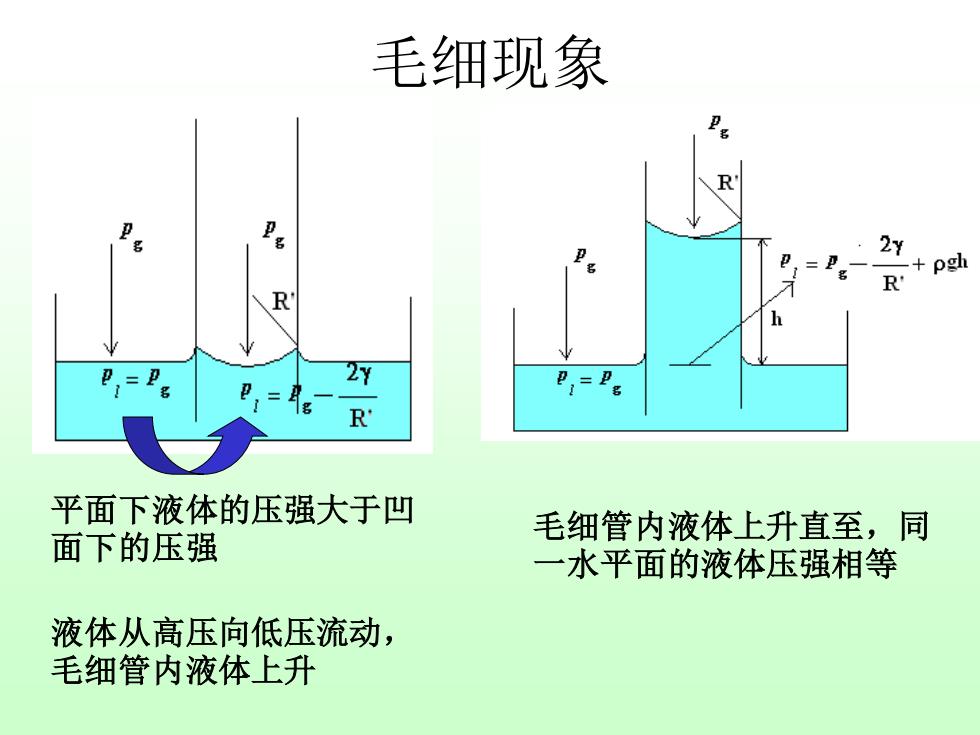
毛细现象 pgh 2Y R 平面下液体的压强大于凹 毛细管内液体上升直至,同 面下的压强 一水平面的液体压强相等 液体从高压向低压流动, 毛细管内液体上升
毛细现象 平面下液体的压强大于凹 面下的压强 液体从高压向低压流动, 毛细管内液体上升 毛细管内液体上升直至,同 一水平面的液体压强相等
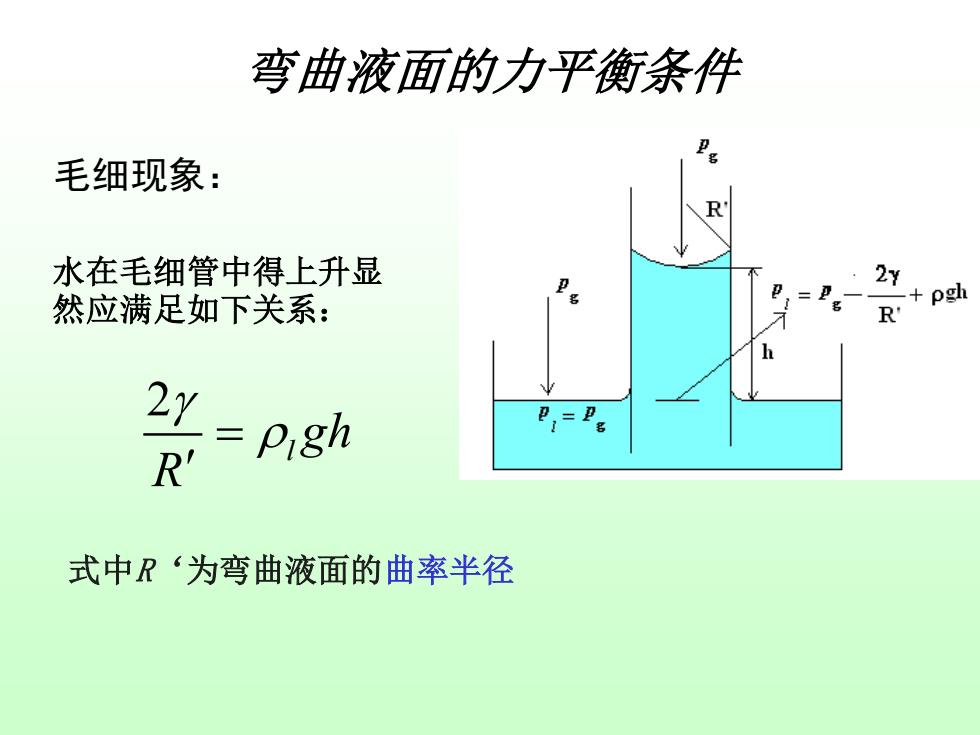
弯曲液面的力平衡条件 毛细现象: R 水在毛细管中得上升显 2y 然应满足如下关系: pgh R 2y =pigh R' 式中R‘为弯曲液面的曲率半径
弯曲液面的力平衡条件 毛细现象: 2 l gh R = 式中R‘为弯曲液面的曲率半径 水在毛细管中得上升显 然应满足如下关系:
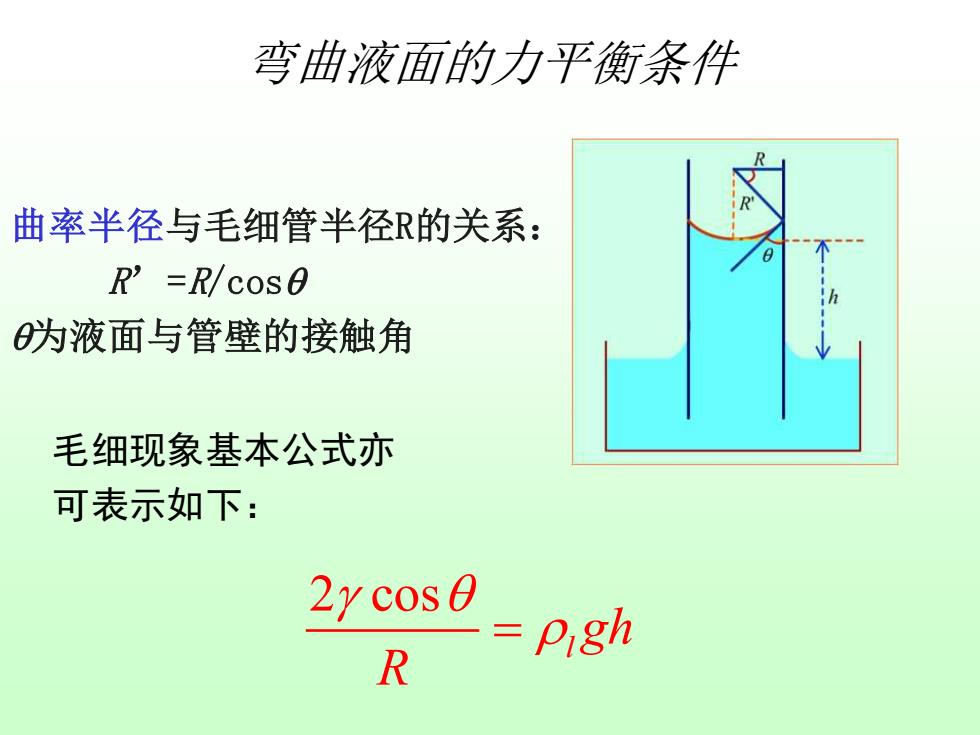
弯曲液面的力平衡条件 曲率半径与毛细管半径R的关系: R'=R/cOS0 为液面与管壁的接触角 毛细现象基本公式亦 可表示如下: 2y cos0 R =pigh
弯曲液面的力平衡条件 2 cos l gh R = 毛细现象基本公式亦 可表示如下: 曲率半径与毛细管半径R的关系: R’=R/cos 为液面与管壁的接触角
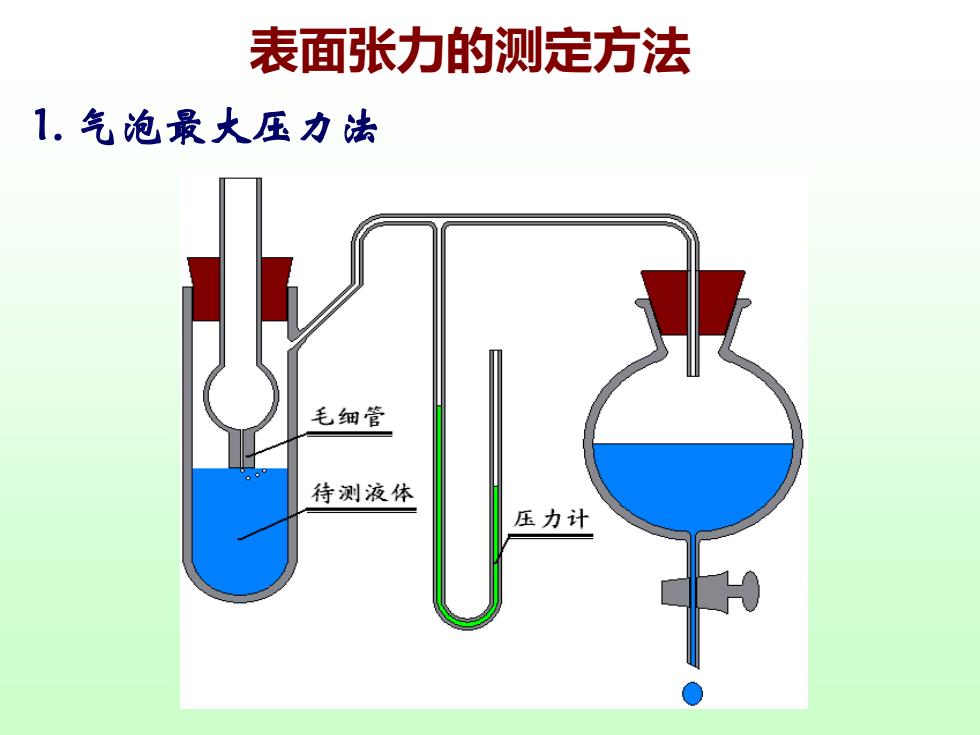
表面张力的测定方法 1.气泡最火压力法 毛细管 待测液体 压力计
表面张力的测定方法 1. 气泡最大压力法