
第三节分部积分法分部积分公式例题小结思考题
第三节 分部积分法 ◼ 分部积分公式 ◼ 例题 ◼ 小结 思考题

分部积分公式一、xeydxarcsinxdx =xIn Xdx-特点被积函数是两个不同函数的乘积解决思路利用两个函数乘积的求导法则设函数u=u(x)及v=v(x)具有连续导数两边积分(uv)'=u'v+uv'=uv'= (uv)'-u'vudx =uv-@vudv=uv-vdu分部积分公式
解决思路 利用两个函数乘积的求导法则. (uv) = uv + uv uv = (uv) − uv = uv dx = udv 分部积分公式 特点 被积函数是两个不同函数的乘积 设函数u = u(x)及v = v(x) 具有连续导数. uv− u vdx uv − vdu 两边积分 一、分部积分公式 xe x = x d arcsinxdx = x ln xdx =
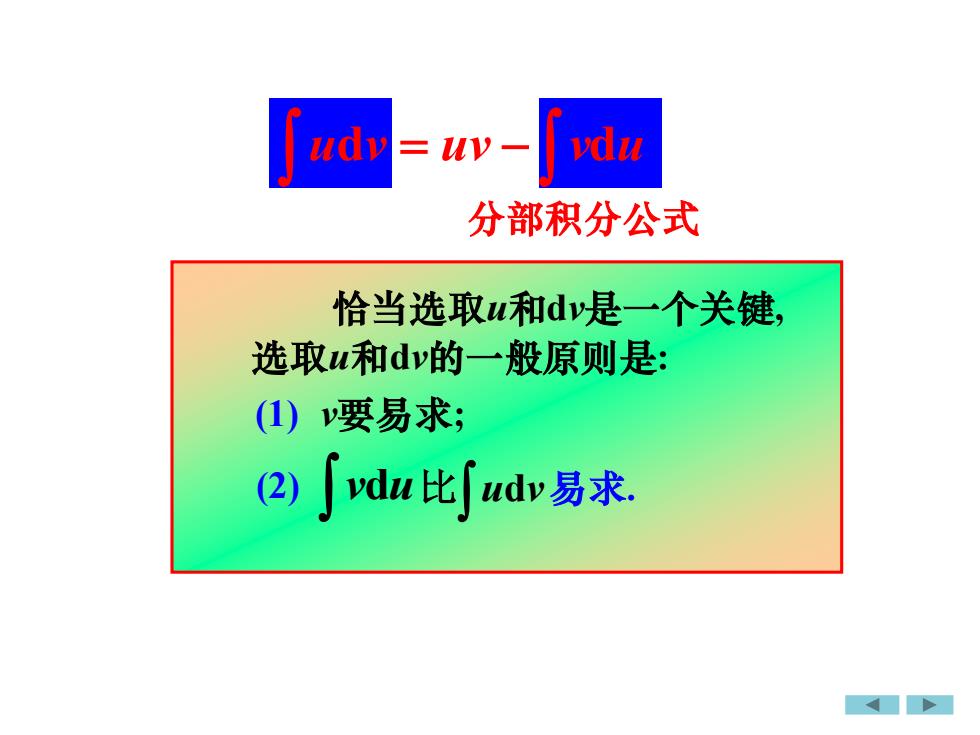
vduudy=uv-分部积分公式恰当选取u和d是一个关键选取u和dv的一般原则是:(1) 要易求;[vdu比[udy易求.(2)
恰当选取u和dv是一个关键, v要易求; udv uv vdu = − 分部积分公式 选取u和dv的一般原则是: vdu (1) (2) 比 udv 易求

[udv = uv - [ vdu二、例题例1求[xcosxdx.解 法一 u=cosx,dv=xdx, v:2du = -sinxdx.22xxcosxdx=sinxdxcos x +22显然,u,dv选择不当,积分更难进行法二 u= x, dv= cosxdxdu=dx, v=sinx(xcos xdx= xsinxsin xdx=xsinx+cosx+C
例1 求 cos d . x x x xcos xdx= x + x cos 2 2 显然, u,dv u = x, dv = cos xdx xcos xdx= xsin x = xsin x + cos x +C 法二 二、例 题 du = dx, v = sin x − sin xdx x x x sin d 2 2 udv uv vdu = − 选择不当, 积分更难进行. 解 法一 u = cos x, dv = xdx, , 2 2 x v = du = -sin xdx

udv = uvvdu x'e*dx.例2 求解 u=x2,dv = edxdu =2xdx, v= ex[x'e*dx=x'e*-xe"dx(再次使用分部积分法)u=x,dv=e*dx=xe*-2(xe*-e*)+C
例2 求 d . 2 x e x x 解 , 2 u = x v e x x d = d x e x x d 2 = − x x e 2 x e xe e C x x x = − 2( − ) + 2 (再次使用分部积分法) u = x, v e x x d = d du = 2xdx, x v = e xe x x 2 d udv uv vdu = −

uUUkxdx,P,()P.(P.()sinaxdx,cosaxdxDe其中k,a为常数P,(x)为n次多项式
P (x)sinaxdx, P (x)cosaxdx, P (x)e dx, kx n n n 其中k,a为常数, u u u Pn (x)为n次多项式

[udv = uv - [ vdu例3求xarctanxdx.u=x,dv=arctanxdxdu=dx, v:解 u=arctanx, dv = xdx.21xdudx.21+ xxarctanxdxdxarctan221+.1)dxarctan x221+x1(x -arctanx) +Carctanx -22
例3 求 arctan d . x x x 解 u = arctan x , 2 2 x v = xarctanxdx = x − x arctan 2 2 = x − x arctan 2 2 x x x C x = − ( − arctan ) + 2 1 arctan 2 2 d , 1 1 d 2 x x u + = dv = xdx udv uv vdu = − x x x d 1 1 2 2 2 + x x )d 1 1 (1 2 1 2 + − u = x, dv = arctan xdx du = dx, v =

-udv = uv-vduI x3 In xdx.例4 求dv = x'dx解 u=lnx,化简型xdu=二dx4x1x31Inxdxdx411C16X
例 4 求 ln d . 3 x x x 解 u = ln x , d v x dx 3 = x ln x dx 3 = x ln x − 41 4 = x x − x + C 4 4 161 ln 41 44 x x v = x u d1 d = 化简型 x dx 41 3 u d v uv vd u = −

uuJ P,(x)arcsin xdx, [ P,(x)arctan xdx,u[ P,(x)nxdx元注利用arcsin x + arccos x =2元arctanx + arccot x :=2'可把P,(x)arccos xdx, ( P,(x)arccot xdx化为[ P,(x)arcsin xdx, ( P,(x)arctan xdx的积分
P ( x )arcsin x dx, P ( x )arctan x dx, n n Pn(x)ln xdx u u u 注 利用 , 2 arcsin arccos x + x = , 2 arctan arccot x + x = 可把 P ( x )arcsin x dx , n 的积分 P ( x )arccos x dx , n 化为 Pn(x)arccot x dx Pn ( x )arctan x dx

应用分部积分法时,可不明显地写出如何选取u、dv,而直接套用公式.(对较简单的情况)例SI尔解sinxdexsin.tdxdyW= e* sin x- [e*d(sinx)= e* sinx - [e' cos xdx= e" sinx - [cosxde'dyu=e* sinx- (e* cosx- [e*dcosx)etsinxdx=e(sinx-cosx)注意循环形式etsinxdx =sinx-cosx)+C2
例5 求 sin d . e x x x 解 e x x x sin d = x sin xde = e x − x sin = e x − e x x x x sin cos d = − x x e sin x cos xde = e x − x sin = e x − x − e x x x x (sin cos ) sin d e x x x sin d x x C e x = (sin − cos ) + 2 注意循环形式 u u dv e d(sin x) x u (e cos x − e dcos x) x x u dv 应用分部积分法时,可不明显地写出如何选 取u、dv,而直接套用公式.(对较简单的情况)