
曲率第七节、孤微分、曲率及其计算公式三、 曲率圆与曲率李径四、小结
第七节 曲率 • 一、弧微分 • 二、曲率及其计算公式 • 三、曲率圆与曲率半径 • 四、小结

一、弧微分V设函数f(x)在区间(a,b)内具有连续导数MA基点: A(xo,yo),xM(x,y)为任意一点0xx规定:(1)曲线的正向与x增大的方向一致;(2)有向弧段AM的值是s,=±|AM|,当AM的方向与曲线正向一致时,s取正号,相反时,s取负号显然s= s(x)是单调增函数
0 0 ( ) ( , ) . : ( , ), ( , ) , f x a b A x y M x y 设函数 在区间 内具有连续导数 基点 为任意一点 A 0 x M x x yo 规定: (1) ; 曲线的正向与x增大的方向一致 (2) , , , , . AM s s AM AM s s 有向弧段 的值是 = , 当 的方 向与曲线正向一致时 取正号 相反时 取负号 显然s s x = ( ) . 是单调增函数 一、弧微分

山设N(x+△x,y+Ay),对应于x的N增量△x,弧s的增量为△s=MN,MARMNMNS( ()I-MMt元Ax0x+ArAxxx(Ax) +(Ay)2MNMN()[1+((△x)?MNMNAxMNAsMN[1+()1土一又: lim±1MNArAXMN4x→0dsASAs=±/1+(y): s= s(x)是单调增函数limdxAx-0Ax: ds = /1 + y"dx弧微分公式
2 s x + = 2 2 2 2 ( ) ( ) ( ) M N x y M N x = + 2 2 [1 ( ) ] M N y M N x 2 0 lim 1 ( ) x ds s y dx x → = = + 0 lim 1 x M N → M N 又 = = + 2 2 [1 ( ) ] s M N y x M N x 2 = + 1 ds y dx N x x y y x ( , ), x s s MN 设 对应于 的 增量 ,弧 的增量为 , + + = N A R 0 x M x x + x x y o s s x = ( ) 是单调增函数 = 2 2 M N M N M N x = 2 M N x 弧微分公式

曲率及其计算公式二、日1、曲率的定义(弯曲程度)的量曲率是描述曲线局部性质Aa2AaM'AS,AS,M2MM3NASAS,NAaM,弧段弯曲程度转角相同弧段越越大转角越大短弯曲程度越大
M1 M3 2 M2 S2 S1 1 M M S1S2 N N 曲率是描述曲线局部性质(弯曲程度)的量. 弧段弯曲程度 越大转角越大 转角相同弧段越 短弯曲程度越大 1、曲率的定义 二、曲率及其计算公式
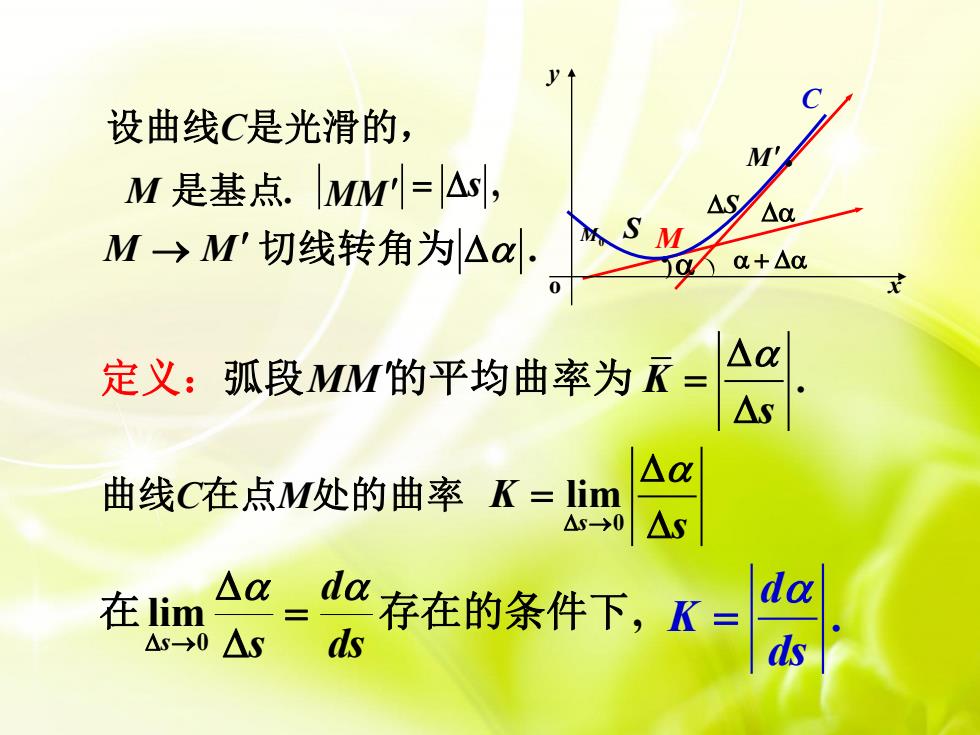
V设曲线C是光滑的,M'M是基点.MM=As,ASAαSMM→M'切线转角为△αα+Aαax0Aα定义:弧段MM的平均曲率为KAsAa曲线C在点M处的曲率 K = limAsAs-0da△αda在lim存在的条件下,K=AsdsAs-0ds
+ S S ) . M. M C M0 y o x MM K . s = 定义:弧段 的平均曲率为 设曲线C是光滑的, M 是基点. MM = s , M M → 切线转角为 . 0 lim s K s → = 曲线C在点M处的曲率 lim , 0 在 存在的条件下 ds d s s = → . d K ds =

注意:(1)直线的曲率处处为零;(2)圆上各点处的曲率等于半径的倒数,且半径越小曲率越大2、曲率的计算公式设y=f(x)二阶可导,:tanα=yJ"有 α =arctany',dα =dx,1+ J"2小"ds = 1+ y'dx. :. K =(1 + y"2)2
2、曲率的计算公式 注意: (1) 直线的曲率处处为零; (2) 圆上各点处的曲率等于半径的倒数,且 半径越小曲率越大. 设y = f (x)二阶可导, tan = y , , 1 2 dx y y d + = 3 2 2 . (1 ) y K y = + 有 = arctan y , 1 . 2 ds = + y dx

x = p(t),设二阶可导,y=y(t),y'(t)d'ydyp'(t)y"(t)-@"(t)y'(t)dr?dxp'(t)p"3(t)@'(t)y"(t) -"(t)y'(t): K=3[g"(t)+y'(t)]
, ( ), ( ), 设 二阶可导 = = y t x t 3 2 2 2 ( ) ( ) ( ) ( ) . [ ( ) ( )] t t t t K t t − = + , ( ) ( ) t t dx dy = . ( ) ( ) ( ) ( ) ( ) 2 3 2 t t t t t dx d y − =

例1 计算等双曲线xy =1在点(1,1)处的曲率2解:由y=得:=-,tsx因此y'|x=I = -1, y"|x=1 =2双曲线xy=1在点(x,y)处的曲率为/22yK=(1 +(-1)")3/2 = 2 = (1 + y"2)3/22
例1 1 (1,1) . 计算等双曲线xy = 在点 处的曲率 2 3 2 2 3 2 | | 2 1 2 (1 ) (1 ( 1) ) 2 2 y K y = = = = + + − 2 3 1 1 2 y y y x x x 解:由 = = − = 得: , 1 1 1, 2 x x 因此 y y = = = − = 双曲线xy x y = 1 ( , ) 在点 处的曲率为

例2 抛物线y=ax2+bx+c上哪一点的曲率最大?解 y'=2ax +b,y"= 2a,[2a.:. K=3[1 +(2ax + b)j3b显然,当x =时,曲率k最大2a62b4ac又(-)为抛物线的顶点2a4a:抛物线在顶点处的曲率最大
例2 ? 抛物线 y = ax2 bx + c 上哪一点的曲率最大 解 y = 2ax + b, y = 2a, 3 2 2 2 . [1 (2 ) ] a K ax b = + + , . 2 b x k a 显然,当 = − 时 曲率 最大 ) , 4 4 , 2 ( 2 又 为抛物线的顶点 a b ac a b − 抛物线在顶点处的曲率最大

例3铁轨由直道转入圆弧弯道时,若接头处的曲率突然改变,容易发生事故,为了行驶平稳,往往在直道和弯道之间接入一段缓冲段(如图),使曲率连续地由零过渡1到二(R为圆弧轨道点击图片任意处播放暂停R的半径)
点击图片任意处播放\暂停 ). ( 1 ( ), , 的半径 到 为圆弧轨道 率连续地由零过渡 缓冲段 如图 使曲 弯道之间接入一段 稳,往往在直道和 的曲率突然改变 容易发生事故,为了行驶平 铁轨由直道转入圆弧弯道时,若接头处 R R 例3