
Power Point 电子科技大学 无源RC滤波器的频率响应特性的研究 电子料越女学 Univarsity of Electrnie Selanca and Tochaaloy f China
电子科技大学 无源RC滤波器的频率响应特性的研究 PowerPoint

内容 实验目的 实验原理 看里售有原年售等生售因■生期自年里年年用年自由售用年年售售自中生售因■性期售年里年年男年自■■■用年售出年年生售男■生样自年● 3 实验内容 4 实验报告要求及思考 电子转线女学
内 容 1 实验目的 2 实验原理 3 实验内容 4 实验报告要求及思考

实验目的 1.掌握RC滤波器的设计方法。 2.掌握滤波器频率特性的点频测试法。 3.进一步掌握示波器、晶体管毫伏表、函数发生器 等仪器的正确使用方法。 电子特线女学
实验目的 1. 掌握RC滤波器的设计方法。 2. 掌握滤波器频率特性的点频测试法。 3. 进一步掌握示波器、晶体管毫伏表、函数发生器 等仪器的正确使用方法
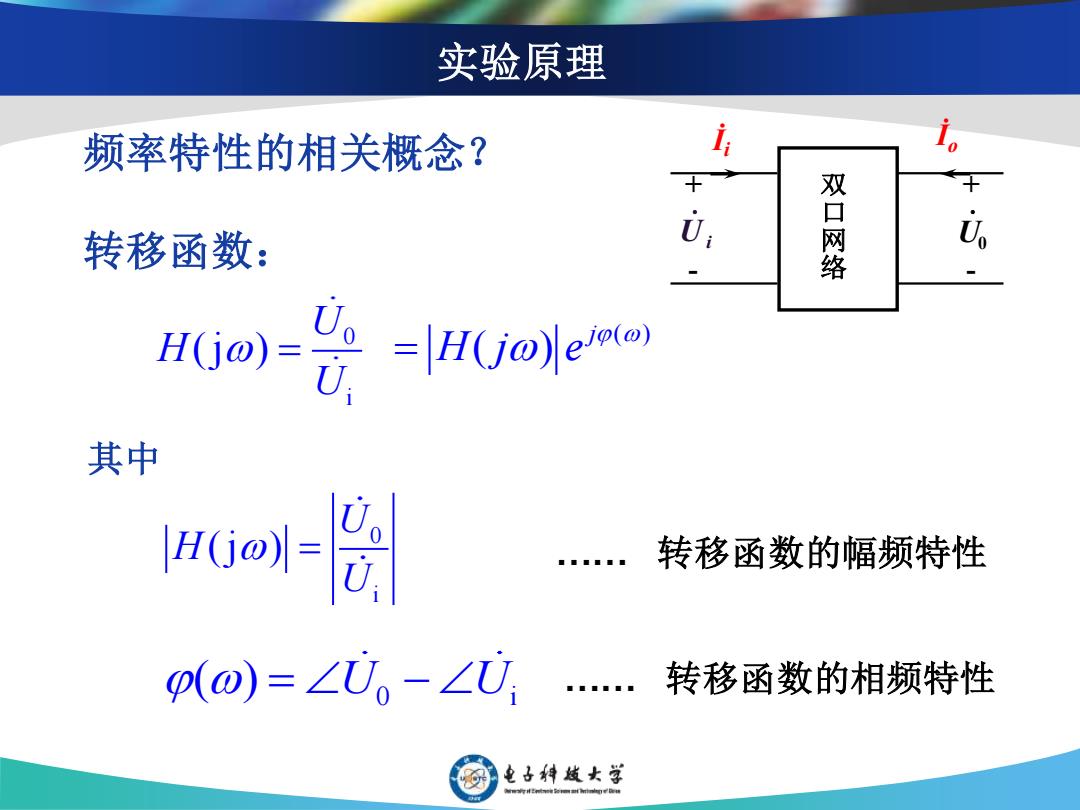
实验原理 频率特性的相关概念? 转移函数: 双口网络 U aUo)=号-Ho 其中 时 …转移函数的幅频特性 0(o)=∠U。-∠U,… 转移函数的相频特性 电子特战女学
实验原理 0 i (j ) U H U = ( ) ( ) j H j e = 0 i (j ) U H U = 频率特性的相关概念? 转移函数: 其中 …… 转移函数的幅频特性 ( ) = − U U 0 i …… 转移函数的相频特性 + - + - 双 口 网 络 Ui & İi İo U0 &
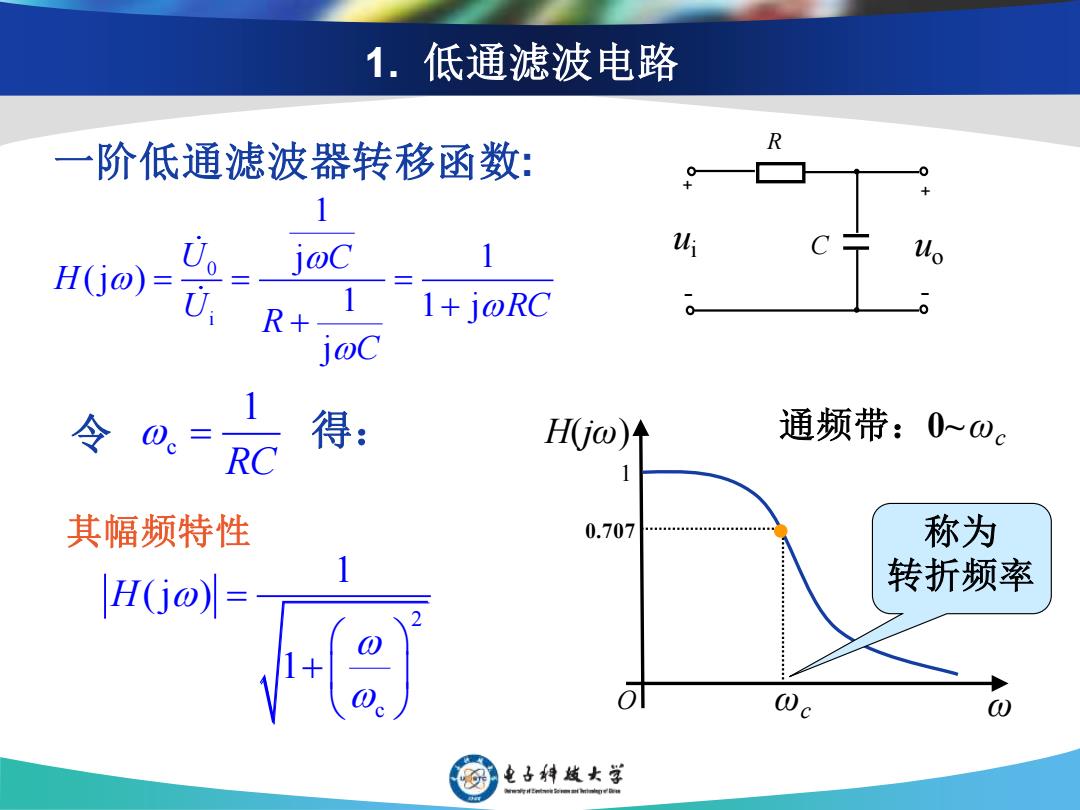
1.低通滤波电路 一阶低通滤波器转移函数: R 1 joC 1 ui Ho)=0 R+ 1+j@RC j@C 令0。= 得: Hω)1 通频带:0~wc RC 其幅频特性 0.707 480810000408 称为 H(= 转折频率 ω 电子特战女学
1. 低通滤波电路 0 i 1 j 1 (j ) 1 1 j j U C H U RC R C = = = + + c 1 RC = ui R C ﹢ ﹢ ﹣ ﹣ uo 一阶低通滤波器转移函数: 令 得: 其幅频特性 0.707 称为 转折频率 通频带:0~ ωc 1 2 c 1 (j ) 1 H = + H(jω) O ωc ω
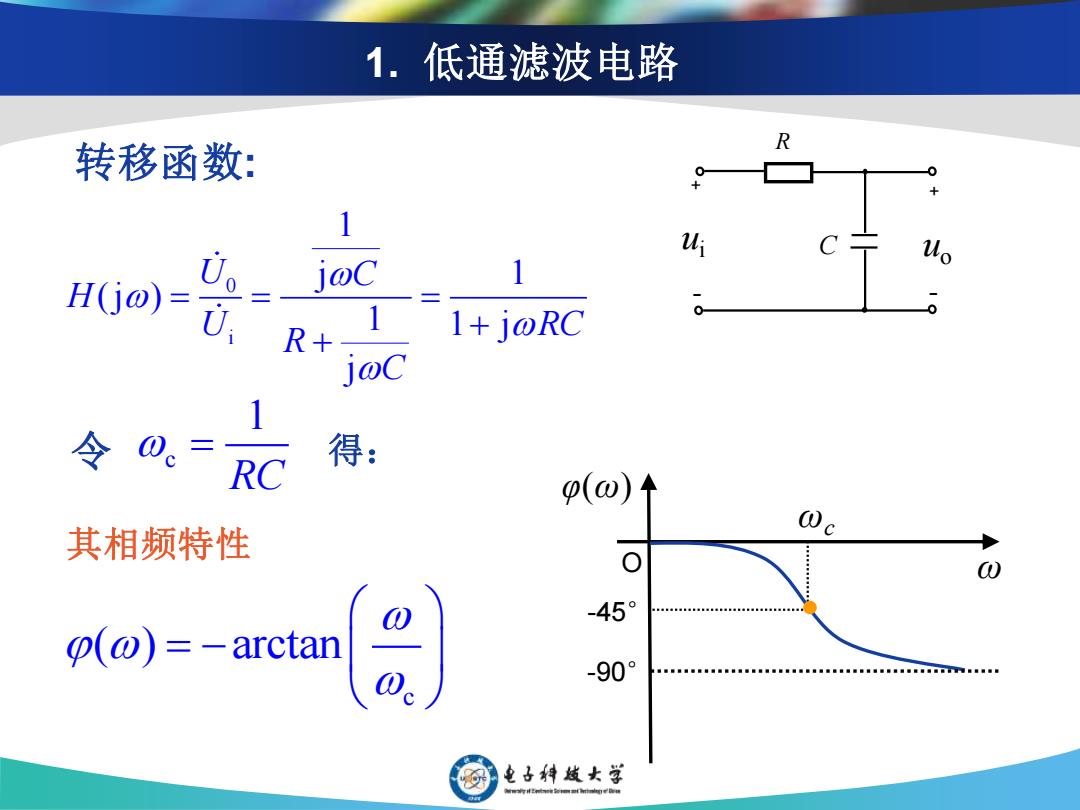
1.低通滤波电路 R 转移函数: H(0o)=U、 joC R+ 1+jRC 令0。= RC 得: 0(ω) Wc 其相频特性 -45° W. -90 电子特越女学
1. 低通滤波电路 0 i 1 j 1 (j ) 1 1 j j U C H U RC R C = = = + + c 1 RC = ui R C ﹢ ﹢ ﹣ ﹣ uo 转移函数: 令 得: 其相频特性 c ( ) arctan = − φ(ω) ωc O ω -45° -90°
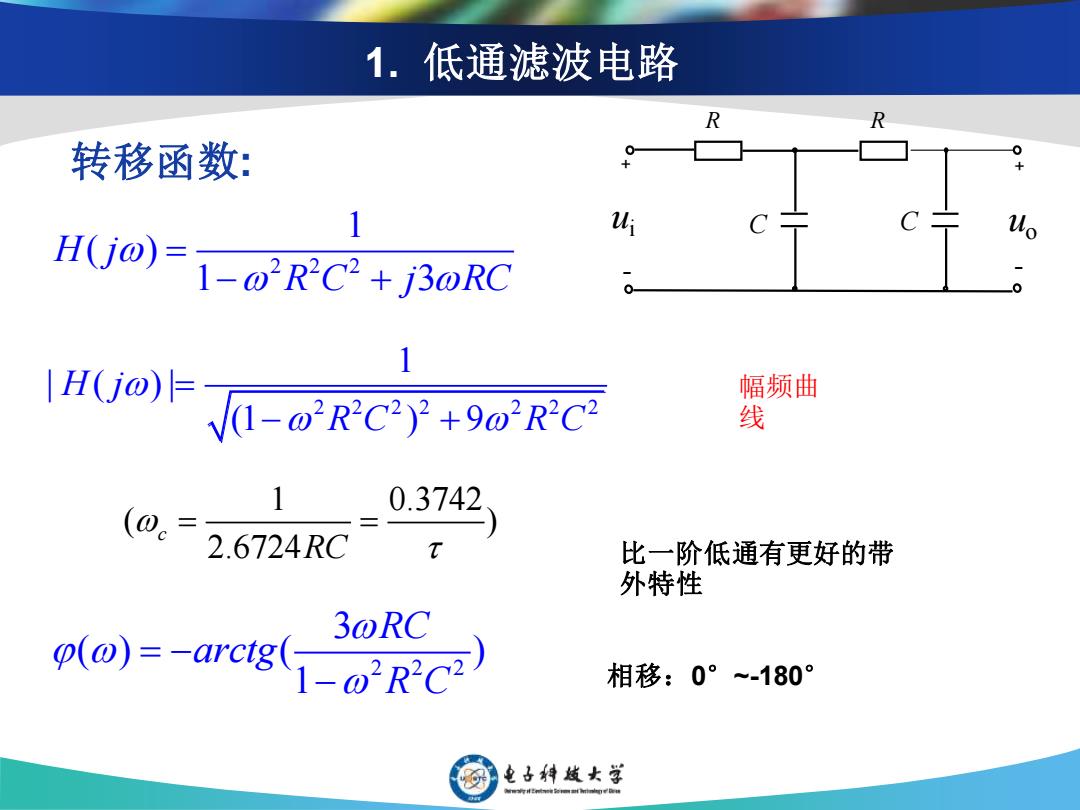
1.低通滤波电路 R R 转移函数: 1 H(j@)=-o'RC2+j3@RC 1 HRCY+9C 频曲 线 (0.2 1_0.3742 2.6724RC 比一阶低通有更好的带 外特性 3@RC 0(o)=-awcg(1-ORc) 相移:0°~-180° 电子转战女学
1. 低通滤波电路 2 2 2 1 ( ) 1 3 H j R C j RC = − + ui R C ﹢ ﹢ ﹣ ﹣ uo R C 2 2 2 2 2 2 2 1 | ( ) | (1 ) 9 H j R C R C = − + 2 2 2 3 ( ) ( ) 1 RC arctg R C = − − 比一阶低通有更好的带 外特性 相移:0°~-180° 1 0.3742 ( ) 2.6724 c RC = = 转移函数: 幅频曲 线

频特 性 电子特妓女学
相频特 性
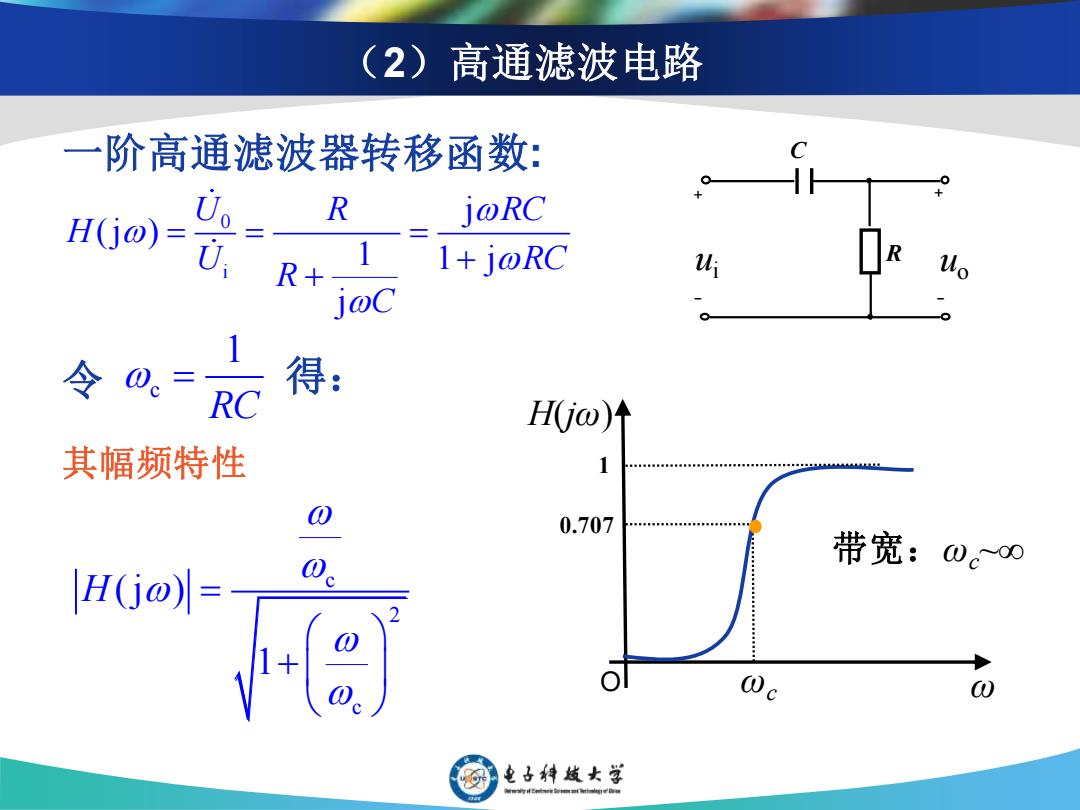
(2)高通滤波电路 一阶高通滤波器转移函数: R H(jo)= Uo joRC 0、 R+ 11+j@RC u uo jwC 令0= 得: H0jω) 其幅频特性 1 0 0.707 带宽:wco0 o 0 电子转战女学
(2)高通滤波电路 0 i j (j ) 1 1 j j U R RC H U RC R C = = = + + c 1 RC = R C ﹢ ﹢ ﹣ ﹣ ui uo 一阶高通滤波器转移函数: 令 得: 其幅频特性 0.707 带宽:ωc~∞ 1 c 2 c (j ) 1 H = + H(jω) O ωc ω

(2)高通滤波电路 转移函数: Uo H(j)=U, R joRC 1 R+ 1+j@RC uo joC 令风= 得: 其相频特性 p(ω)4 90° p(o)=90°-arctan 45° 电子特越女学
(2)高通滤波电路 0 i j (j ) 1 1 j j U R RC H U RC R C = = = + + c 1 RC = 转移函数: 令 得: 其相频特性 90° 45° c ( ) 90 arctan = − R C ﹢ ﹢ ﹣ ﹣ ui uo φ(ω) O ωc ω