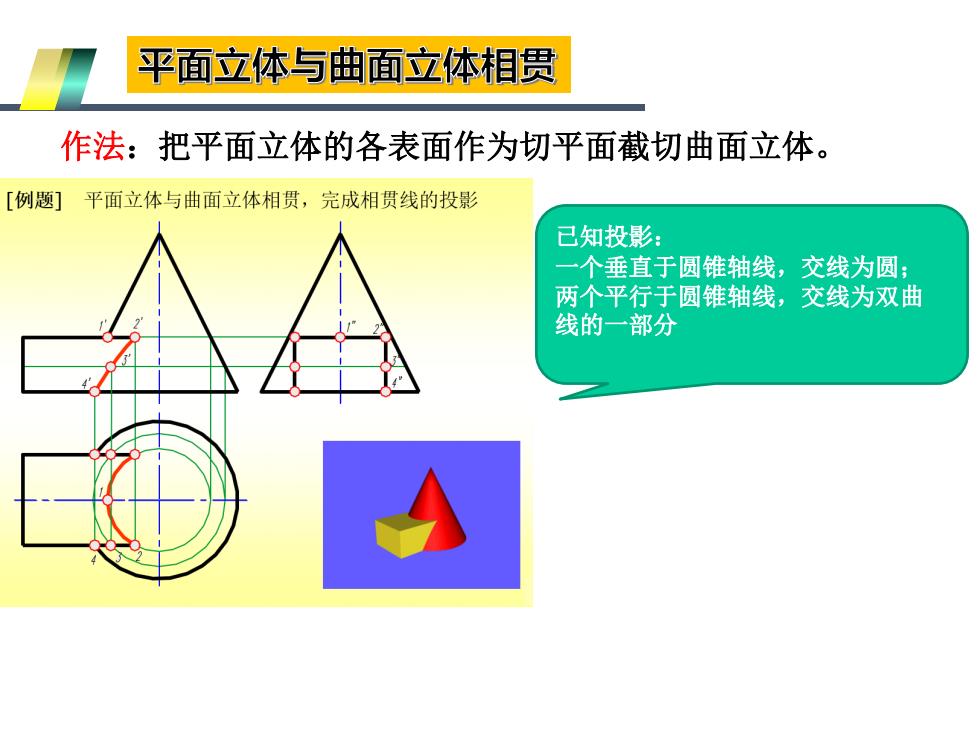
平面立体与曲面立体相贯 作法:把平面立体的各表面作为切平面截切曲面立体。 [例题]平面立体与曲面立体相贯,完成相贯线的投影 已知投影: 一个垂直于圆锥轴线,交线为圆; 两个平行于圆锥轴线,交线为双曲 线的一部分
作法:把平面立体的各表面作为切平面截切曲面立体。 已知投影: 一个垂直于圆锥轴线,交线为圆; 两个平行于圆锥轴线,交线为双曲 线的一部分
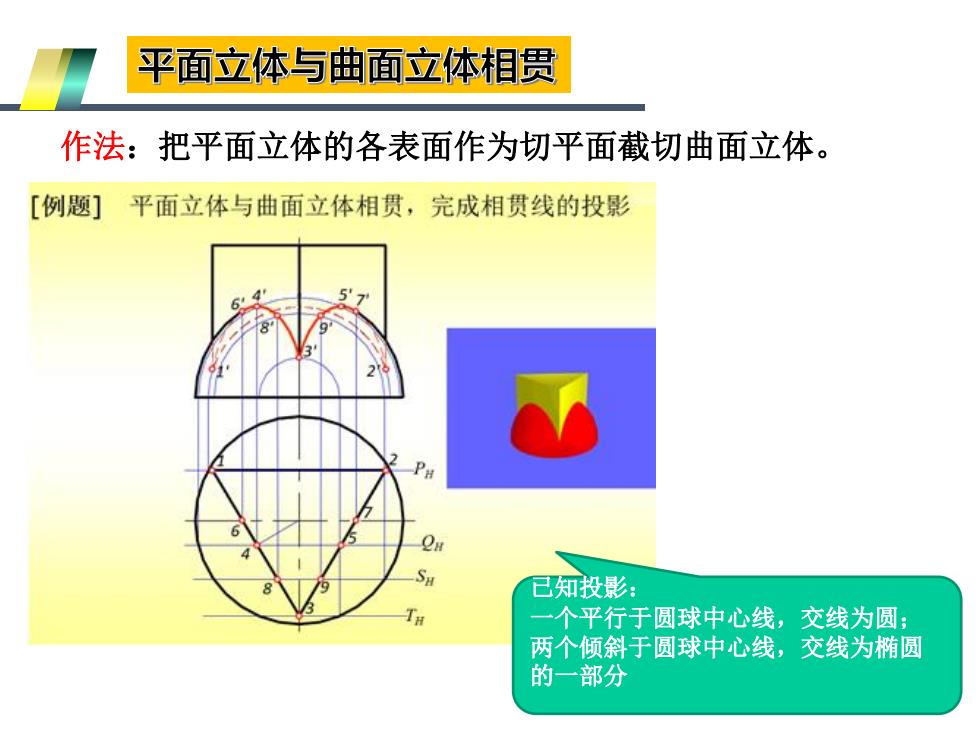
平面立体与曲面立体相贯 作法:把平面立体的各表面作为切平面截切曲面立体。 [例题] 平面立体与曲面立体相贯,完成相贯线的投影 6 已知投影: 一个平行于圆球中心线,交线为圆: 两个倾斜于圆球中心线,交线为椭圆 的一部分
作法:把平面立体的各表面作为切平面截切曲面立体。 已知投影: 一个平行于圆球中心线,交线为圆; 两个倾斜于圆球中心线,交线为椭圆 的一部分
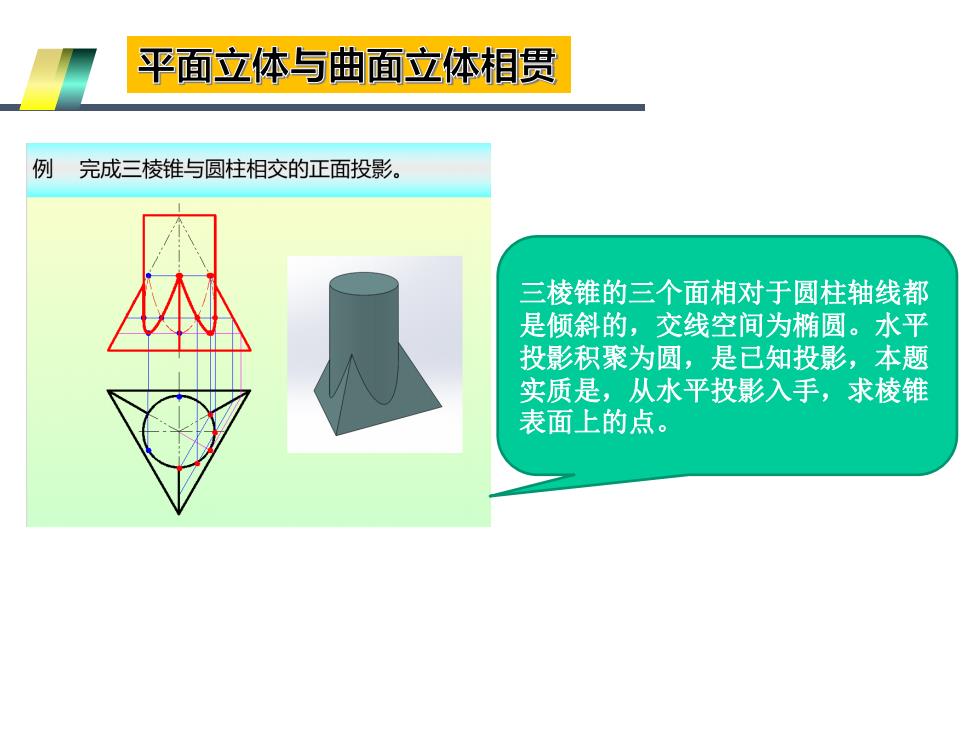
平面立体与曲面立体相贯 例 完成三棱锥与圆柱相交的正面投影。 三棱锥的三个面相对于圆柱轴线都 是倾斜的,交线空间为椭圆。水平 投影积聚为圆,是已知投影,本题 实质是,从水平投影入手,求棱锥 表面上的点
三棱锥的三个面相对于圆柱轴线都 是倾斜的,交线空间为椭圆。水平 投影积聚为圆,是已知投影,本题 实质是,从水平投影入手,求棱锥 表面上的点
平面立体与曲面立体相贯 步骤总结: 1.从具有积聚性的投影(已知投影)入手,看各个截平面相对于曲面立体(中 轴线)的位置,分析交线形状: 2.分截面依次作出交线 如果交线是直线或圆,可直接作出;如果交线是曲线,需描点作出。 3.处理轮廓,完成投影图 注意曲线的连点顺序、虚实判断的技巧方法。 平血立体与恤直立体相篮。完成相贯线的投彬 【例题]平面立体与曲面立体相贯,完成相贯线的投影 例完成三棱锥与圆柱相交的正面投影
步骤总结: 1.从具有积聚性的投影(已知投影)入手,看各个截平面相对于曲面立体(中 轴线)的位置,分析交线形状; 2.分截面依次作出交线 如果交线是直线或圆,可直接作出;如果交线是曲线,需描点作出。 3. 处理轮廓,完成投影图 注意曲线的连点顺序、虚实判断的技巧方法
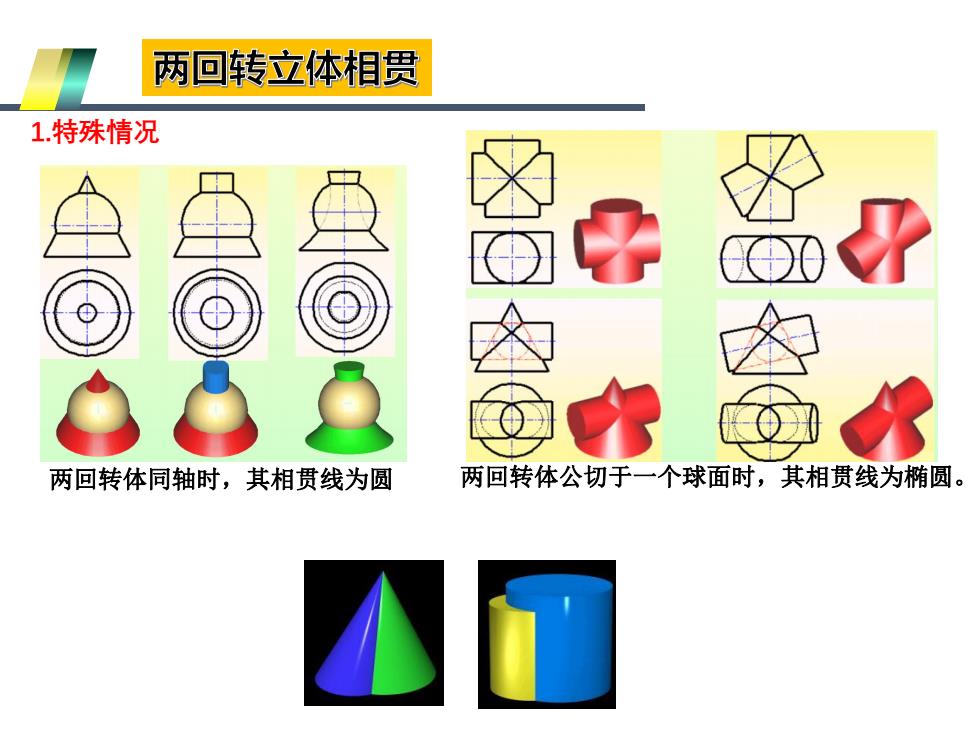
两回转立体相贯 1.特殊情况 两回转体同轴时,其相贯线为圆 两回转体公切于一个球面时,其相贯线为椭圆
1.特殊情况 两回转体同轴时,其相贯线为圆 两回转体公切于一个球面时,其相贯线为椭圆
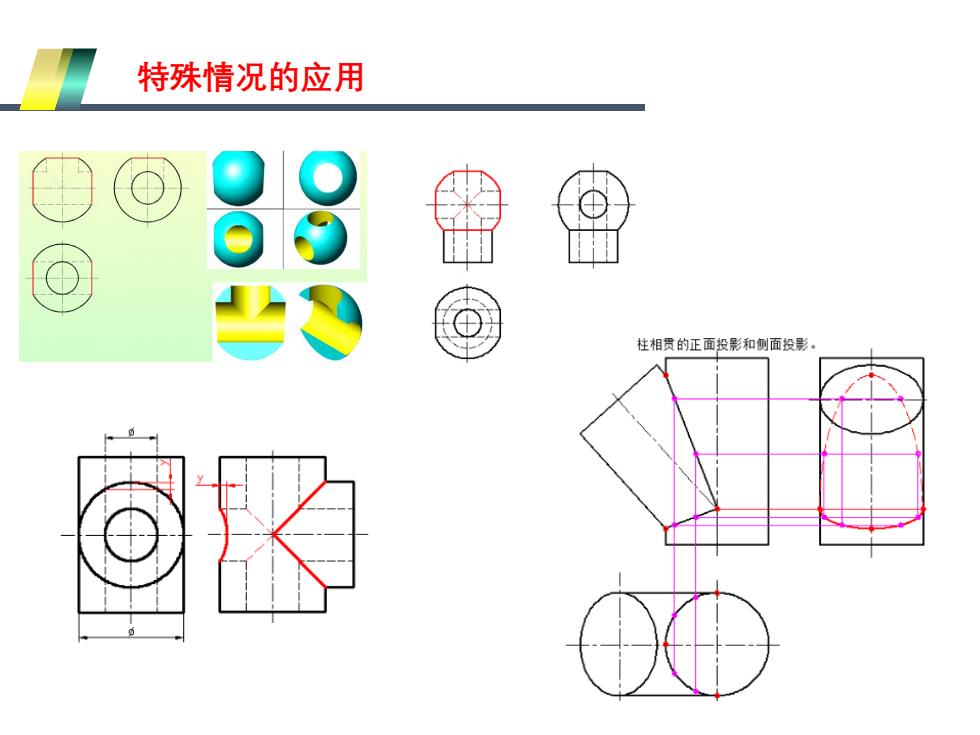
特殊情况的应用 柱相贵的正面投影和侧面投影
特殊情况的应用
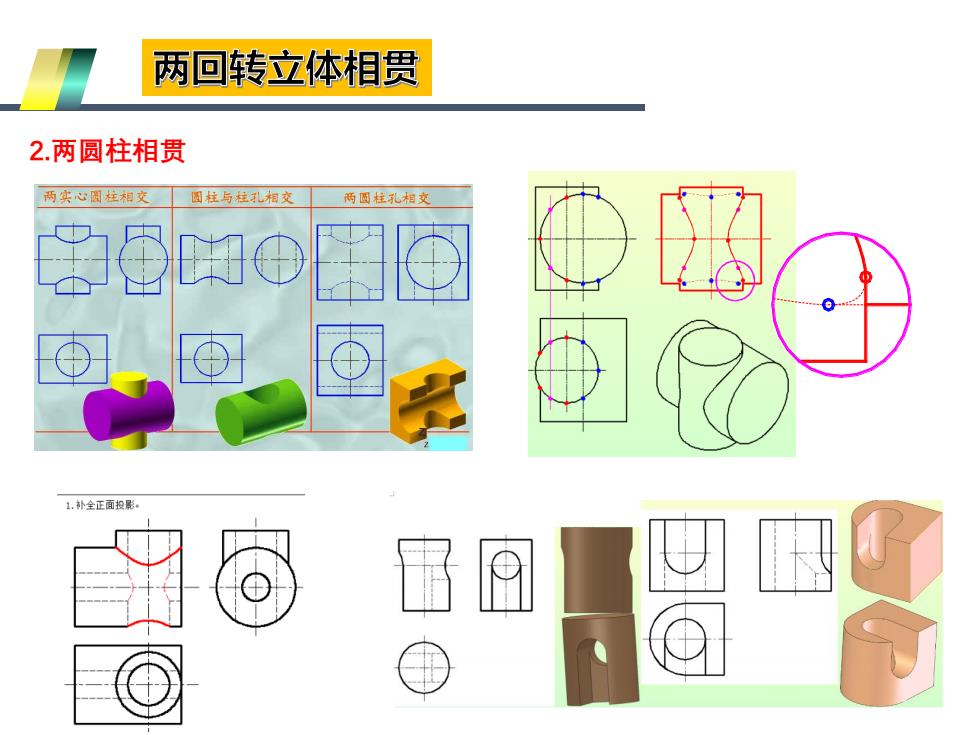
两回转立体相贯 2.两圆柱相贯 两实心圆柱相交 圆柱与柱孔相交 两圆柱孔相交 1.补全正面投影
2.两圆柱相贯
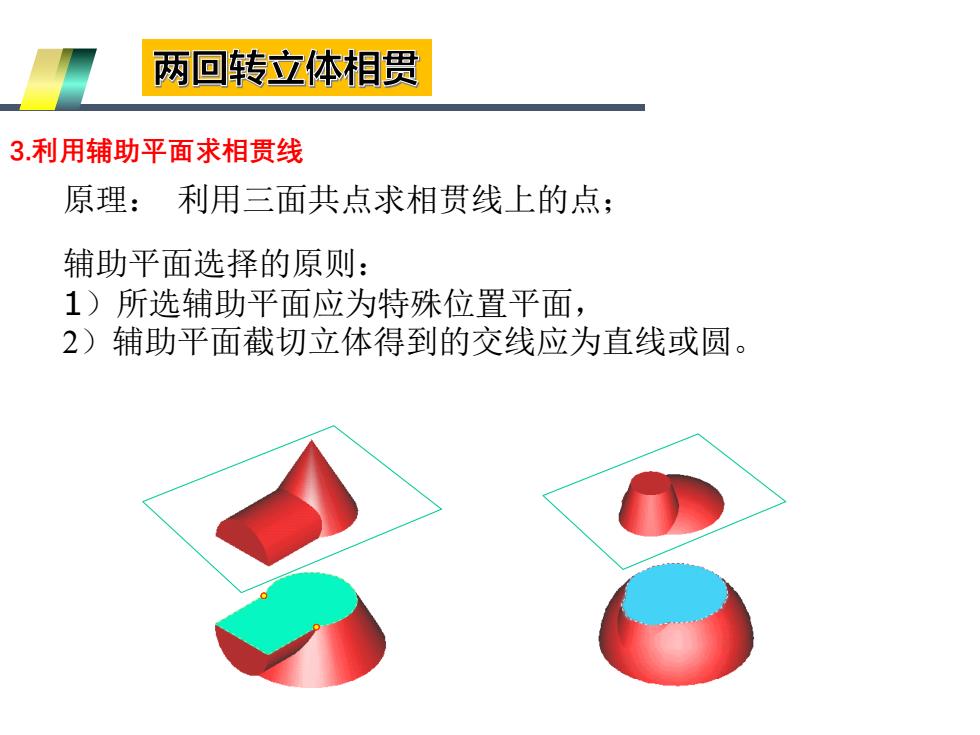
两回转立体相贯 3利用辅助平面求相贯线 原理:利用三面共点求相贯线上的点; 辅助平面选择的原则: 1)所选辅助平面应为特殊位置平面, 2)辅助平面截切立体得到的交线应为直线或圆
3.利用辅助平面求相贯线 原理: 利用三面共点求相贯线上的点; 辅助平面选择的原则: 1)所选辅助平面应为特殊位置平面, 2)辅助平面截切立体得到的交线应为直线或圆
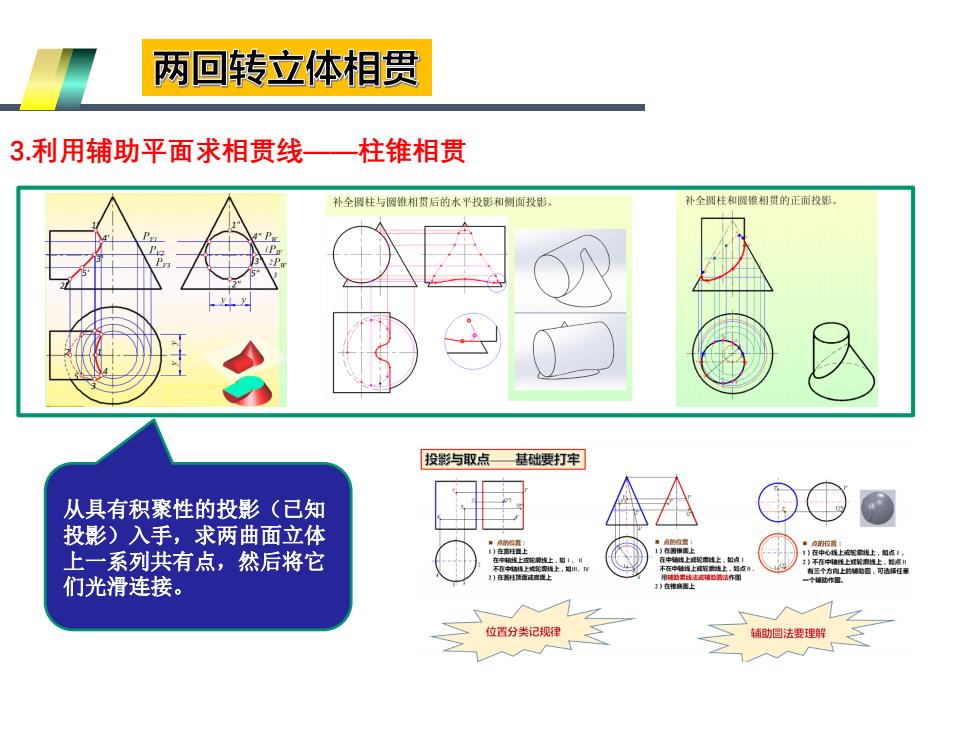
两回转立体相贯 3利用辅助平面求相贯线 柱锥相贯 补全圆柱与圆维相贯后的水平投影和制面投影。 补全圆柱和圆维相贯的正而投影 投影与取点基础要打牢 从具有积聚性的投影(已知 投影)入手,求两曲面立体 上一系列共有点,然后将它 们光滑连接。 】在离H谈宝成立成上 位置分类记规律 辅助圆法要理解
3.利用辅助平面求相贯线——柱锥相贯 从具有积聚性的投影(已知 投影)入手,求两曲面立体 上一系列共有点,然后将它 们光滑连接
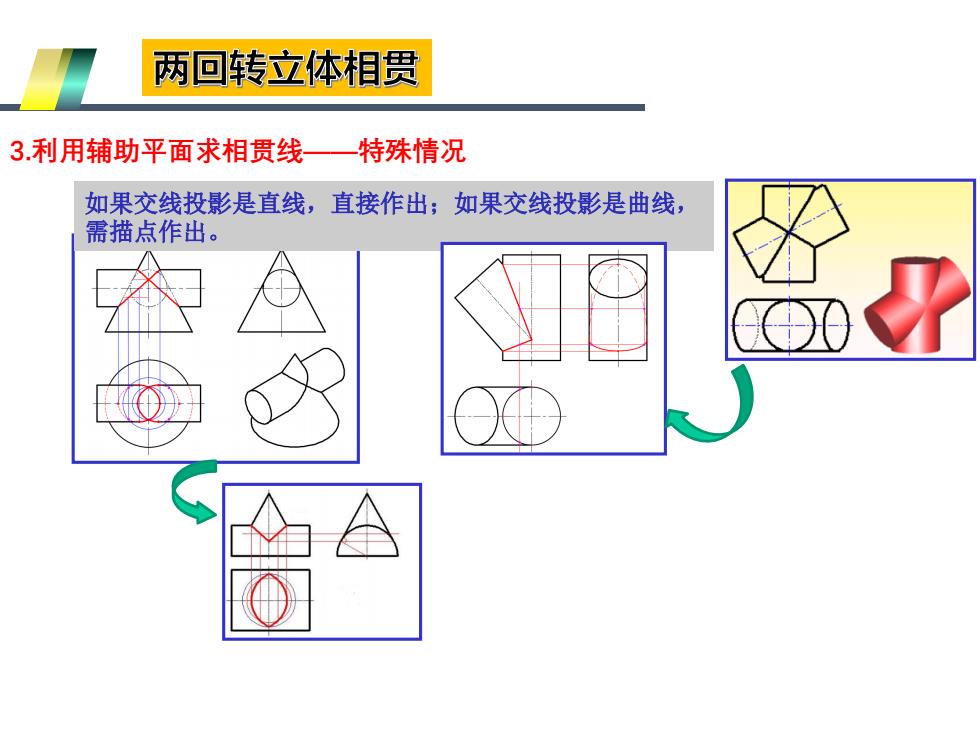
两回转立体相贯 3利用辅助平面求相贯线 特殊情况 如果交线投影是直线,直接作出;如果交线投影是曲线, 需描点作出
如果交线投影是直线,直接作出;如果交线投影是曲线, 需描点作出。 3.利用辅助平面求相贯线——特殊情况