
§2-1投影基本知识 ●● ·●● ●0● ●●● ●●● O
§2-1 投影基本知识
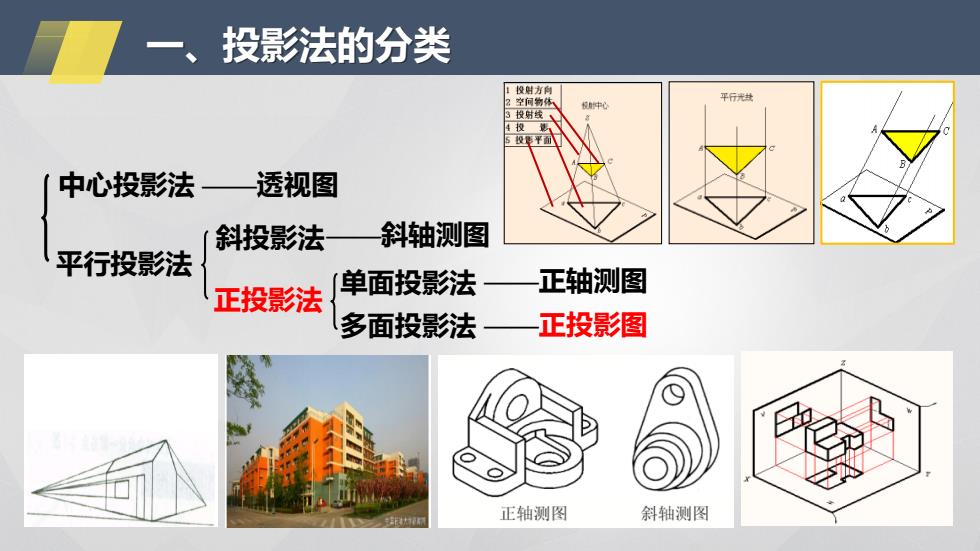
投影法的分类 投附方胸 2空何物体 平行光线 中心 3投射线、 5设平面1 中心投影法 —一透视图 斜投影法 斜轴测图 平行投影法 正轴测图 正投影法 单面投影法 多面投影法— 正投影图 正轴测图 斜轴测图
——透视图 平行投影法 中心投影法 斜投影法 正投影法 单面投影法 多面投影法 ——斜轴测图 ——正轴测图 ——正投影图 一、投影法的分类
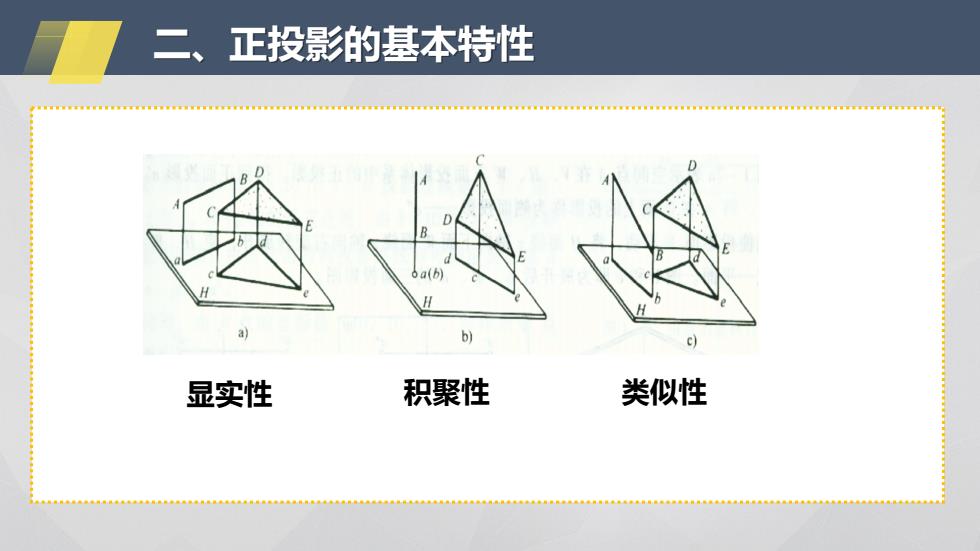
二、正投影的基本特性 a c) 显实性 积聚性 类似性
二、正投影的基本特性 显实性 积聚性 类似性
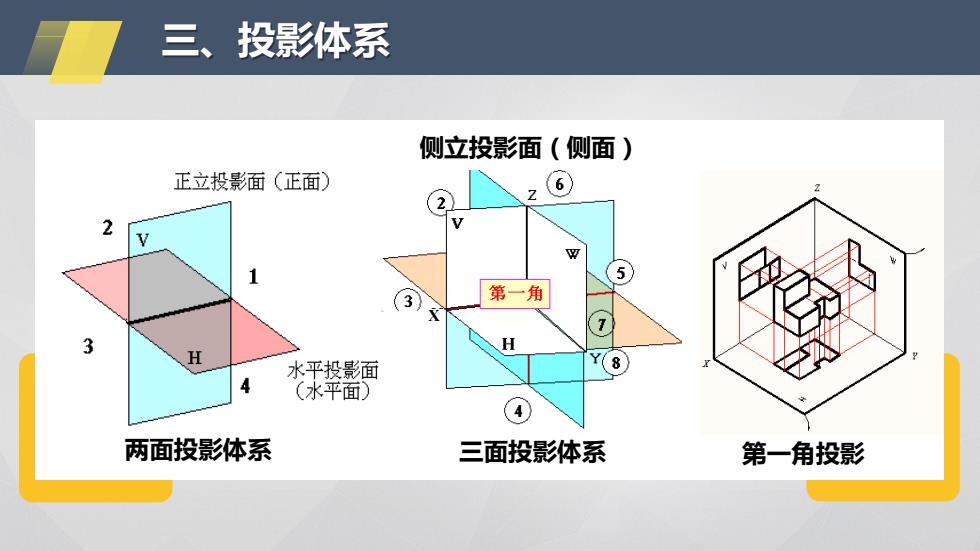
三、投影体系 侧立投影面(侧面) 正立投影面(正面) 6 3】 第一角 3 H 水平投影面 (8 (水平面) 两面投影体系 三面投影体系 第一角投影
第一角投影 三、投影体系 两面投影体系 X 侧立投影面(侧面) 三面投影体系

§2-2-1点的投影 ●● a●● ●●● ●●● ●●● O
§2-2-1 点的投影

一、点的三面投影 Z n水平投影a a n正面投影a' A X W n侧面投影a”" a Y
V W X Z Y O a ′ a A n 水平投影a n 正面投影a′ a ′′ 一、点的三面投影 n 侧面投影a″
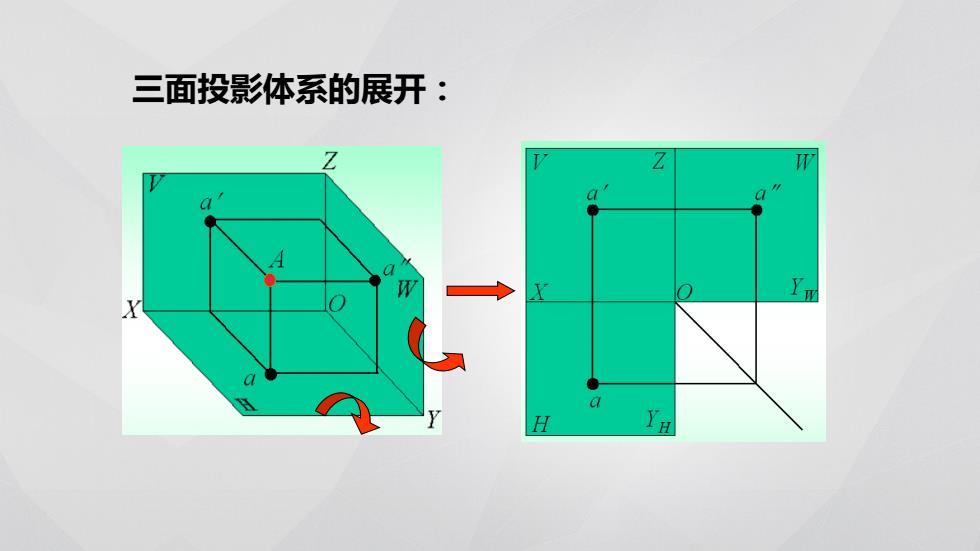
三面投影体系的展开: Y H
三面投影体系的展开:
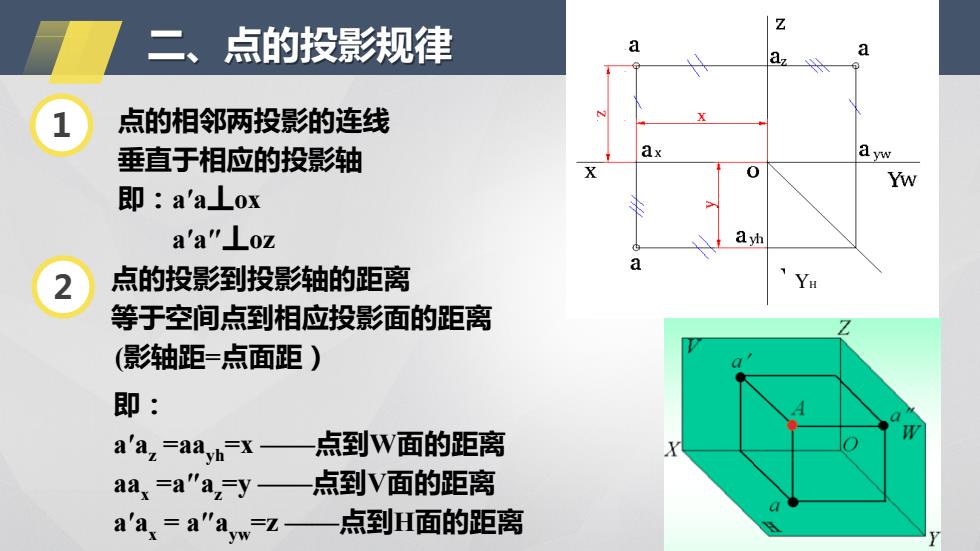
二、 点的投影规律 a az a 1 点的相邻两投影的连线 垂直于相应的投影轴 ax ayw 0 w 即:a'aLox a'a"Loz ayh 点的投影到投影轴的距离 a YH 等于空间点到相应投影面的距离 (影轴距=点面距) 即: a'a,=aayh-x 一点到W面的距离 aax=a"a,-y— 点到V面的距离 a a'a,=a"aw-Z 点到H面的距离
点的相邻两投影的连线 垂直于相应的投影轴 即:a′a 丄ox a′a″ 丄oz 二、点的投影规律 点的投影到投影轴的距离 Y HY H 等于空间点到相应投影面的距离 (影轴距=点面距) 即: a′a z =aayh=x ——点到 W面的距离 aa x =a″a z =y ——点到 V面的距离 a′a x = a″ayw=z ——点到 H面的距离 12
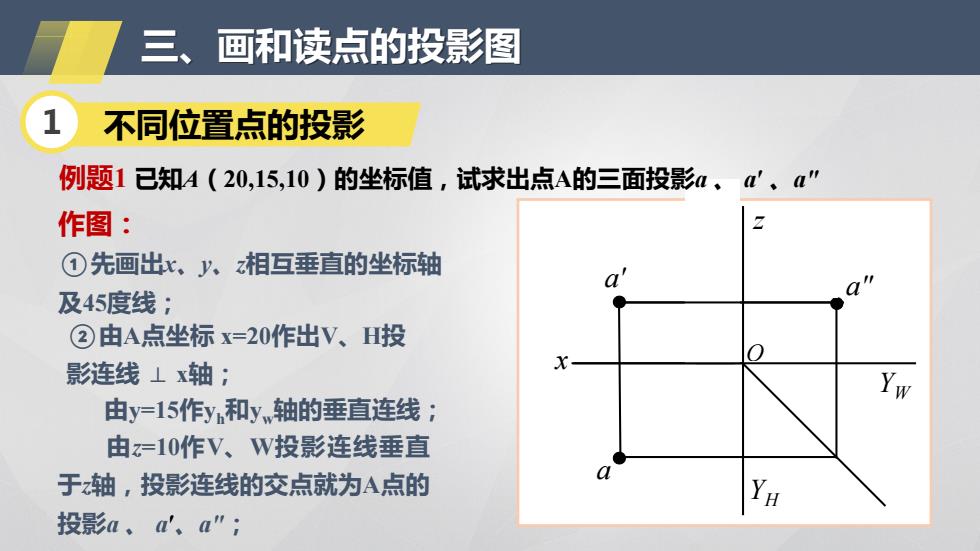
三、画和读点的投影图 不同位置点的投影 例题1已知4(20,15,10)的坐标值,试求出点A的三面投影、d'、a” 作图: ①先画出x、八、相互垂直的坐标轴 及45度线: ②由A点坐标x=20作出V、H投 影连线⊥x轴; Yw 由y=15作y和y轴的垂直连线; 由z=10作V、W投影连线垂直 于轴,投影连线的交点就为A点的 H 投影a、'、a”;
O z YW a" 30 25 20 15 10 5 m m 10 20 5 15 m m x 10 20 5 15 m m 例题1 已知A(20,15,10)的坐标值,试求出点A的三面投影a 、 a′ 、a" 作图: ①先画出x、y、z相互垂直的坐标轴 及45度线; ②由A点坐标 x=20作出V、H投 影连线 ⊥ x轴; 由y=15作yh和yw轴的垂直连线; 由z=10作V、W投影连线垂直 于z轴,投影连线的交点就为A点的 投影a 、 a′ 、a"; YH a a' 三、画和读点的投影图 1 不同位置点的投影
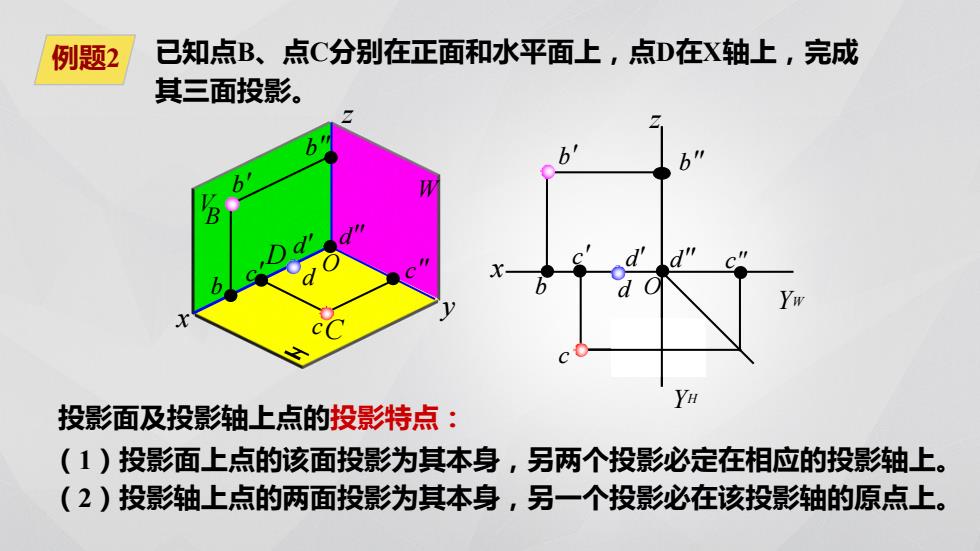
例题2 已知点B、点C分别在正面和水平面上,点D在X轴上,完成 其三面投影。 YH 投影面及投影轴上点的投影特点: (1)投影面上点的该面投影为其本身,另两个投影必定在相应的投影轴上。 (2)投影轴上点的两面投影为其本身,另一个投影必在该投影轴的原点上
x O z YH YW b" O x W V z b' B y b" c " d' d b c ' d" b' b c ' c " D d' c" d ? cC c d" 投影面及投影轴上点的投影特点: (1)投影面上点的该面投影为其本身,另两个投影必定在相应的投影轴上。 (2)投影轴上点的两面投影为其本身,另一个投影必在该投影轴的原点上。 O 已知点B、点C分别在正面和水平面上,点D在X轴上,完成 其三面投影。 例题2