
形象思维与工程语言 杨培中博士副教授 上海交通大学 pzyang@sjtu.edu.cn 1
1 形象思维与工程语言 杨培中 博士 副教授 上海交通大学 pzyang@sjtu.edu.cn

建模与优化 2
2 建模与优化

96 1.工程设计不仅仅是给出一个方案,而是要给出一个 最佳方案。 2.通常情况下,最佳方案会受到各种约束的影响,如 可用资源,法律规定等。 3.优化问题通常比较复杂,需要长时间的试凑方法。 有些情况下,可使用解析方法。 4.要使用解析方法,首先需要将关心的优化量进行解 析表达。 3
3 1. 工程设计不仅仅是给出一个方案,而是要给出一个 最佳方案。 2. 通常情况下,最佳方案会受到各种约束的影响,如 可用资源,法律规定等。 3. 优化问题通常比较复杂,需要长时间的试凑方法。 有些情况下,可使用解析方法。 4. 要使用解析方法,首先需要将关心的优化量进行解 析表达

学习目标 1.理解解析建模与优化的重要性。 2.利用微积分和线性规划方法提出并解决简单问题。 3.理解平坦式最优和陡峭式最优以及偏离最优时的参数选 择。 4
4 1. 理解解析建模与优化的重要性。 2. 利用微积分和线性规划方法提出并解决简单问题。 3. 理解平坦式最优和陡峭式最优以及偏离最优时的参数选 择。 学习目标

解析建模 建立数学模型 1.列出你的需求 2.列出所有可能的关系式 。 质量守恒 动量守恒 能量守恒 资金守恒 几何关系 。 物理关系 3.消去冗余关系 4.检查量纲 5
5 建立数学模型 1. 列出你的需求 2. 列出所有可能的关系式 • 质量守恒 • 动量守恒 • 能量守恒 • 资金守恒 • 几何关系 • 物理关系 3. 消去冗余关系 4. 检查量纲 解析建模

优化一微积分方法 为了优化,首先要将目标函数进行表达,目标函数应表示成 独立变量的函数。 如果目标函数(如成本)能表示成: F=F(x1,X2,) 则最优解可通过对F进行微分,然后让导数为零得到。 f F =…=0 1 原则上,还须求出二阶导数以确定是否为最大或最小解。 6
6 为了优化,首先要将目标函数进行表达,目标函数应表示成 独立变量的函数。 如果目标函数(如成本)能表示成: 则最优解可通过对F进行微分,然后让导数为零得到。 原则上,还须求出二阶导数以确定是否为最大或最小解。 优化—微积分方法 F F x1 , x2 , F x1 F x2 0

优化 通常,目标函数会有一个或多个约束。 G(x2,)≤01=1,2.… H(1,x2,)=0i=1,2… 7
7 优化 通常,目标函数会有一个或多个约束。 Gi x1 , x2 , 0;i 1,2 Hi x1 , x2 , 0;i 1,2
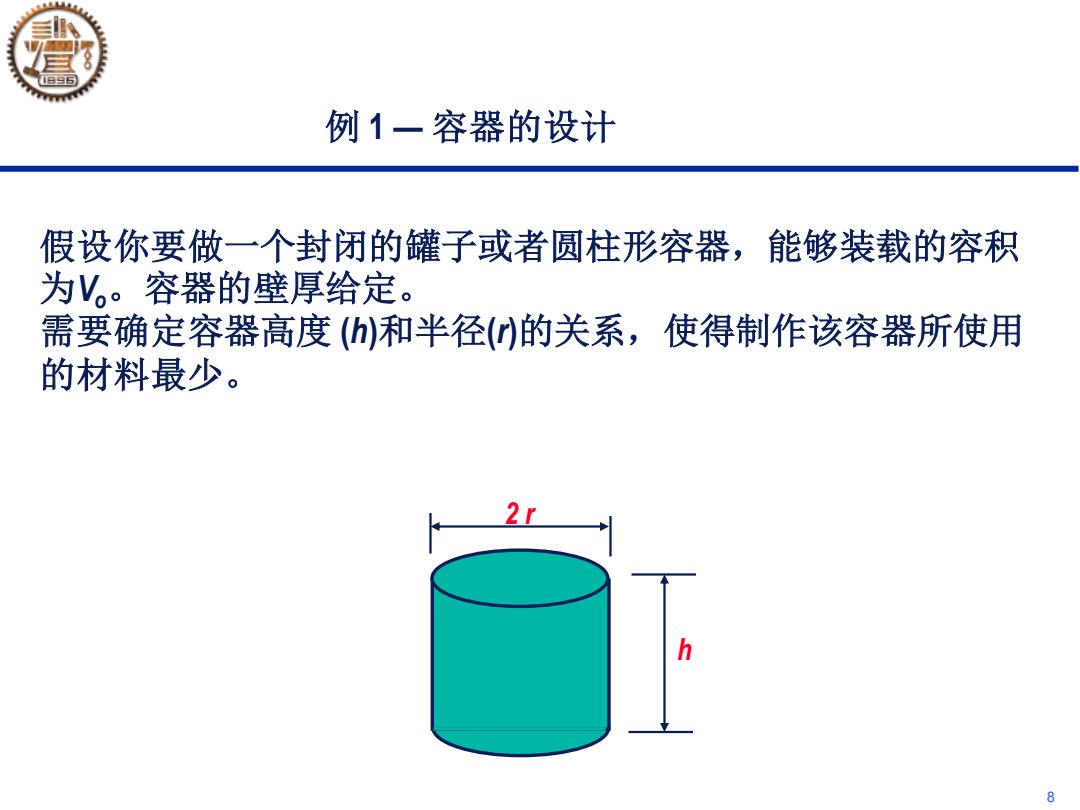
例1一容器的设计 假设你要做一个封闭的罐子或者圆柱形容器,能够装载的容积 为V。容器的壁厚给定。 需要确定容器高度(h)和半径)的关系,使得制作该容器所使用 的材料最少。 8
8 例 1 — 容器的设计 假设你要做一个封闭的罐子或者圆柱形容器,能够装载的容积 为Vo。容器的壁厚给定。 需要确定容器高度 (h)和半径(r)的关系,使得制作该容器所使用 的材料最少。 h 2 r

例1一容器的设计 假定该容器壁厚很小,相对于高度或半径可以忽略不计。 容器的容积为: %=π2h 表面积为: S=2πrh+2z2 消去高度参数,有: S=2亚+2m2 9
9 Vo r 2 h S 2 rh 2 r 2 假定该容器壁厚很小,相对于高度或半径可以忽略不计。 容器的容积为: 表面积为: 消去高度参数,有: S 2Vo r 2r 2 例 1 — 容器的设计

例1一容器的设计 对半径求导,并令其为零,有: ds dr 2y+4πr=0 or 2=3 4π 将容积公式带入,得: h=2r 或者说:直径与高度相等。 10
10 dS dr 2Vo r 2 4 r 0 2Vo 4 r 3 h 2r 对半径求导,并令其为零,有: or 将容积公式带入,得: 或者说:直径与高度相等。 例 1 — 容器的设计