
形象思维与工程语言 杨培中博士副教授 上海交通大学 pzyang@sjtu.edu.cn 1
1 形象思维与工程语言 杨培中 博士 副教授 上海交通大学 pzyang@sjtu.edu.cn

工程中的不确定性-02 > 上讲回顾 > 复合统计 统计过程控制 > 概率 > 回归 2
2 工程中的不确定性-02 上讲回顾 复合统计 统计过程控制 概率 回归

上讲回顾 1.数据表示方法 2.直方图和累积分布 3.均值和标准偏差 4.连续分布 5.正态分布及其应用 3
3 上讲回顾 1. 数据表示方法 2. 直方图和累积分布 3. 均值和标准偏差 4. 连续分布 5. 正态分布及其应用

上讲回顾 例- (回顾) 4
4 例-III (回顾) 上讲回顾
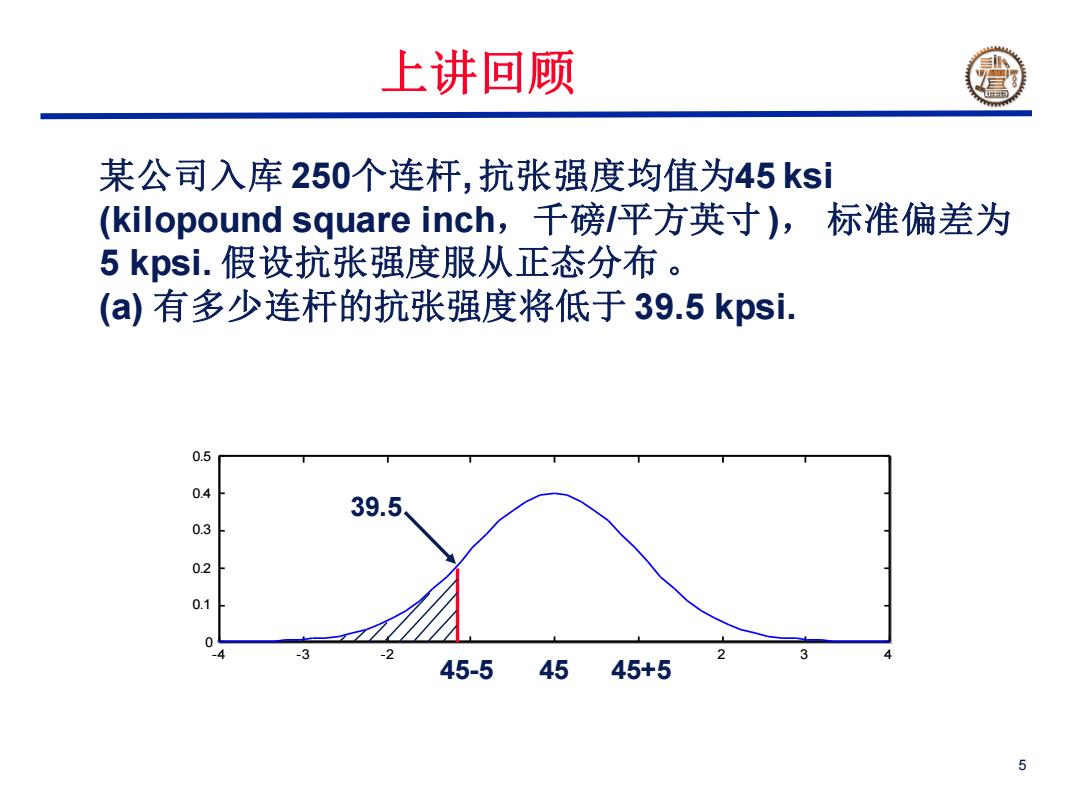
上讲回顾 某公司入库250个连杆,抗张强度均值为45ksi (kilopound square inch,千磅/平方英寸),标准偏差为 5kpsi.假设抗张强度服从正态分布。 (a有多少连杆的抗张强度将低于39.5kpsi. 0.5 0.4 39.5 0.3 02 0.1 3 -2 2 3 45-545 45+5 5
5 某公司入库 250个连杆, 抗张强度均值为45 ksi (kilopound square inch,千磅/平方英寸 ), 标准偏差为 5 kpsi. 假设抗张强度服从正态分布 。 (a) 有多少连杆的抗张强度将低于 39.5 kpsi. -4 -3 -2 -1 0 1 2 3 4 0 0.1 0.2 0.3 0.4 0.5 45-5 45 45+5 39.5 上讲回顾
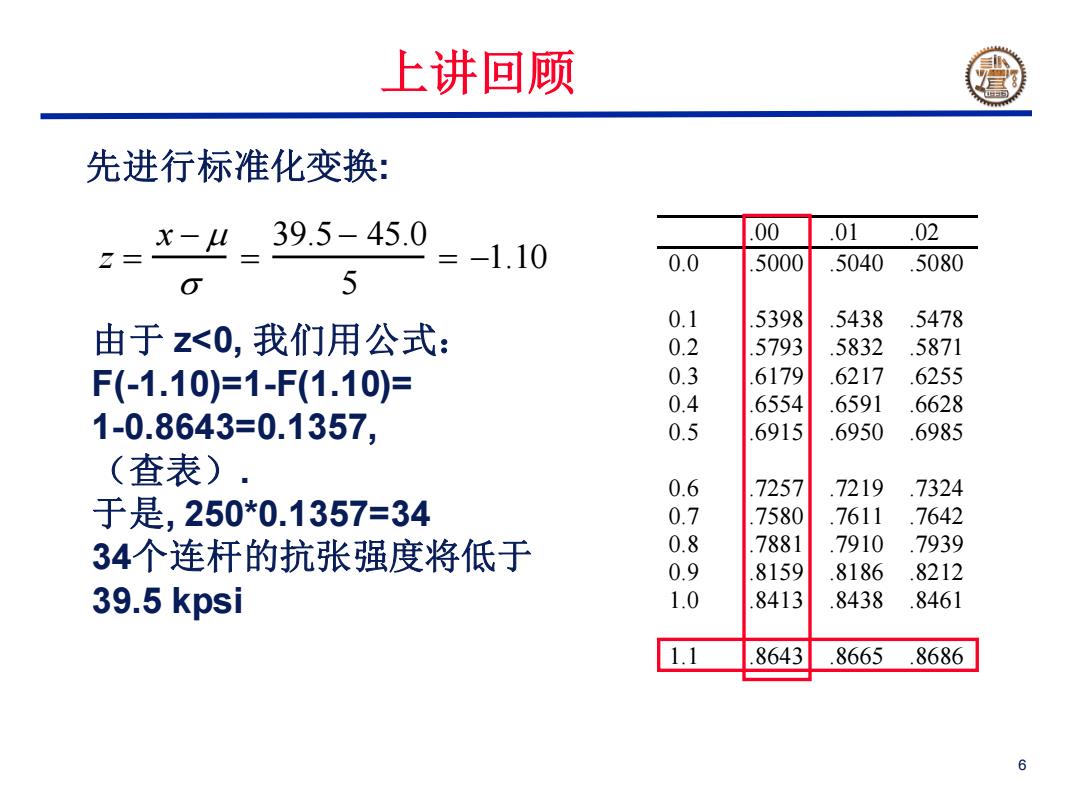
上讲回顾 先进行标准化变换: x-u 39.5-45.0 00 01 02 =-1.10 0.0 5000 .5040 .5080 G 5 0.1 5398 .5438 .5478 由于z<0,我们用公式: 0.2 5793 5832 5871 F(-1.10)=1-F(1.10)= 0.3 6179 6217 6255 0.4 6554 6591 6628 1-0.8643=0.1357, 0.5 6915 6950 6985 (查表). 0.6 7257 .7219 .7324 于是,250*0.1357=34 0.7 7580 .7611 .7642 34个连杆的抗张强度将低于 0.8 7881 .7910 .7939 0.9 8159 .8186 8212 39.5 kpsi 1.0 8413 8438 .8461 1.1 8643 8665 8686 6
6 由于 z<0, 我们用公式: F(-1.10)=1-F(1.10)= 1-0.8643=0.1357, (查表). 于是, 250*0.1357=34 34个连杆的抗张强度将低于 39.5 kpsi z x 39.5 45.0 5 1.10 先进行标准化变换: .00 .01 .02 0.0 .5000 .5040 .5080 0.1 .5398 .5438 .5478 0.2 .5793 .5832 .5871 0.3 .6179 .6217 .6255 0.4 .6554 .6591 .6628 0.5 .6915 .6950 .6985 0.6 .7257 .7219 .7324 0.7 .7580 .7611 .7642 0.8 .7881 .7910 .7939 0.9 .8159 .8186 .8212 1.0 .8413 .8438 .8461 1.1 .8643 .8665 .8686 上讲回顾
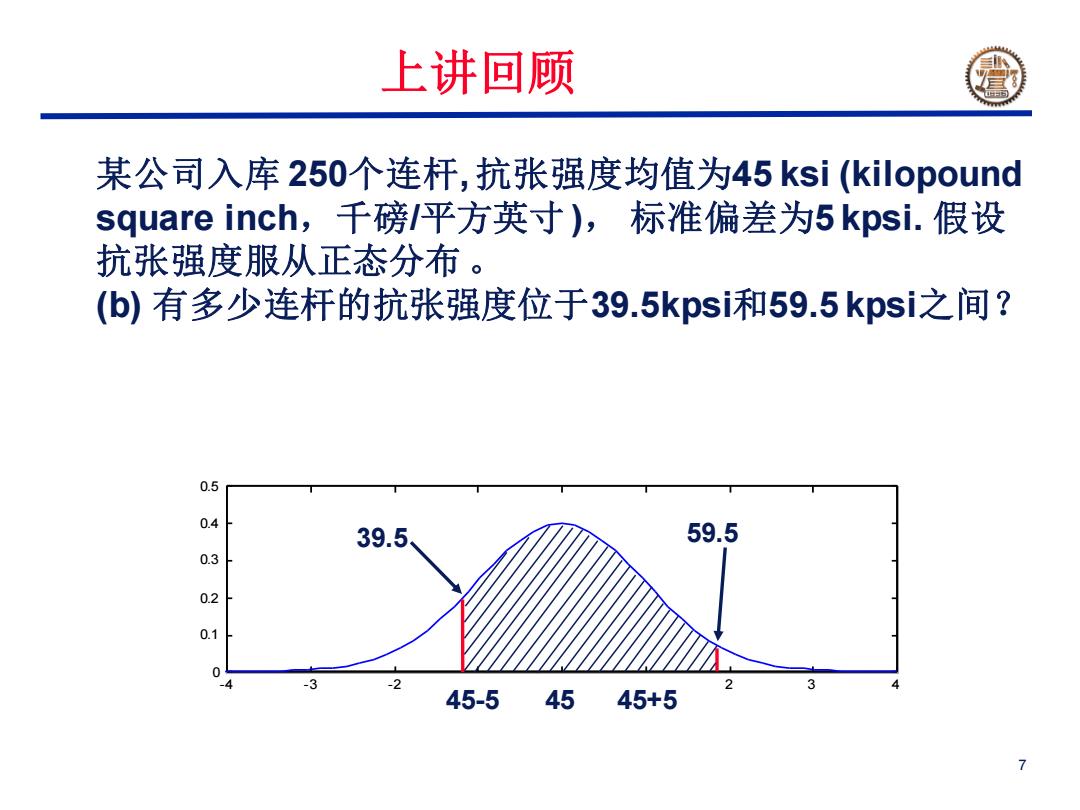
上讲回顾 某公司入库250个连杆,抗张强度均值为45ksi(kilopound square inch,千磅/平方英寸),标准偏差为5kpsi.假设 抗张强度服从正态分布。 (b)有多少连杆的抗张强度位于39.5kpsi和59.5kpsi之间? 0.5 04 39.5 59.5 0.3 0.2 0.1 0 -3 -2 3 45-545 45+5 7
7 某公司入库 250个连杆, 抗张强度均值为45 ksi (kilopound square inch,千磅/平方英寸 ), 标准偏差为5 kpsi. 假设 抗张强度服从正态分布 。 (b) 有多少连杆的抗张强度位于39.5kpsi和59.5 kpsi之间? -4 -3 -2 -1 0 1 2 3 4 0 0.1 0.2 0.3 0.4 0.5 45-5 45 45+5 39.5 59.5 上讲回顾
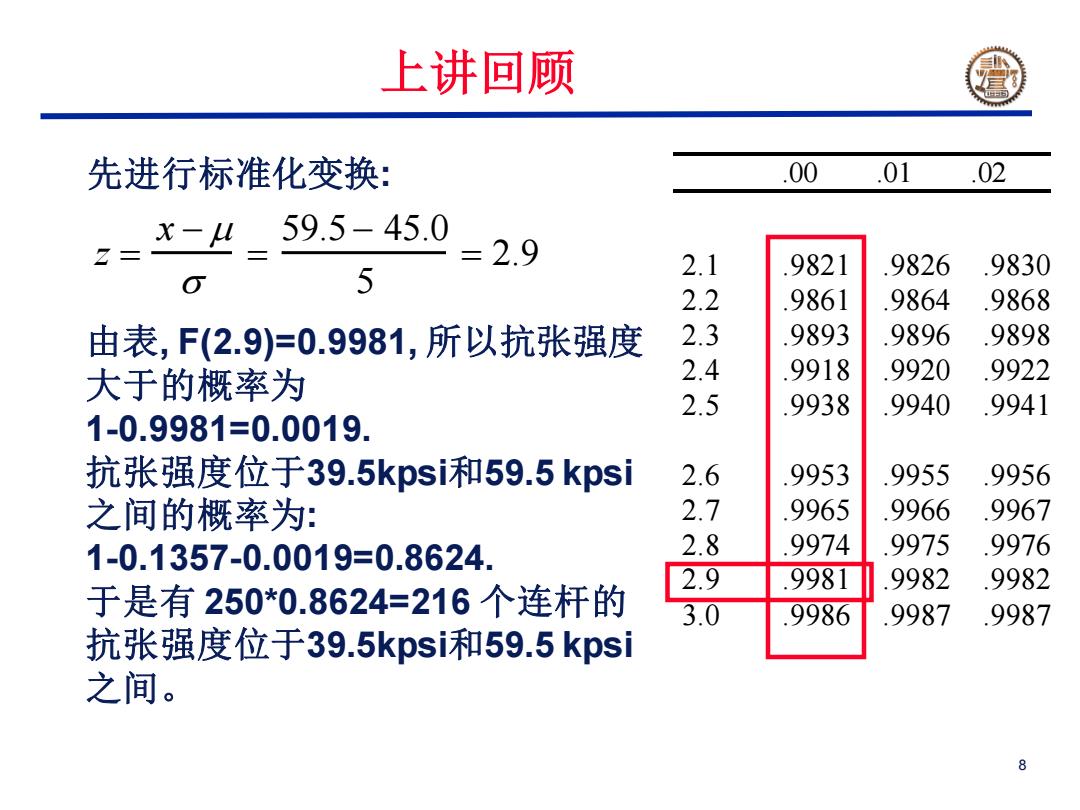
上讲回顾 先进行标准化变换: 00 .01 .02 59.5-45.0 2 x-4 2.9 5 2.1 9821 9826 .9830 2.2 9861 9864 .9868 由表,F(2.9)=0.9981,所以抗张强度 2.3 9893 .9896 .9898 大于的概率为 2.4 9918 .9920 .9922 2.5 .9938 .9940 .9941 1-0.9981=0.0019. 抗张强度位于39.5kpsi和59.5kpsi 2.6 9953 .9955 .9956 之间的概率为: 2.7 9965 .9966 .9967 1-0.1357-0.0019=0.8624. 2.8 9974 .9975 .9976 2.9 9981 9982 9982 于是有250*0.8624=216个连杆的 3.0 9986 9987 .9987 抗张强度位于39.5kpsi和59.5kpsi 之间。 8
8 z x 59.5 45.0 5 2.9 由表, F(2.9)=0.9981, 所以抗张强度 大于的概率为 1-0.9981=0.0019. 抗张强度位于39.5kpsi和59.5 kpsi 之间的概率为: 1-0.1357-0.0019=0.8624. 于是有 250*0.8624=216 个连杆的 抗张强度位于39.5kpsi和59.5 kpsi 之间。 先进行标准化变换: 2.1 .9821 .9826 .9830 2.2 .9861 .9864 .9868 2.3 .9893 .9896 .9898 2.4 .9918 .9920 .9922 2.5 .9938 .9940 .9941 2.6 .9953 .9955 .9956 2.7 .9965 .9966 .9967 2.8 .9974 .9975 .9976 2.9 .9981 .9982 .9982 3.0 .9986 .9987 .9987 .00 .01 .02 上讲回顾

上讲回顾 课堂练习1 (3分钟) 9
9 课堂练习1 (3 分钟) 上讲回顾
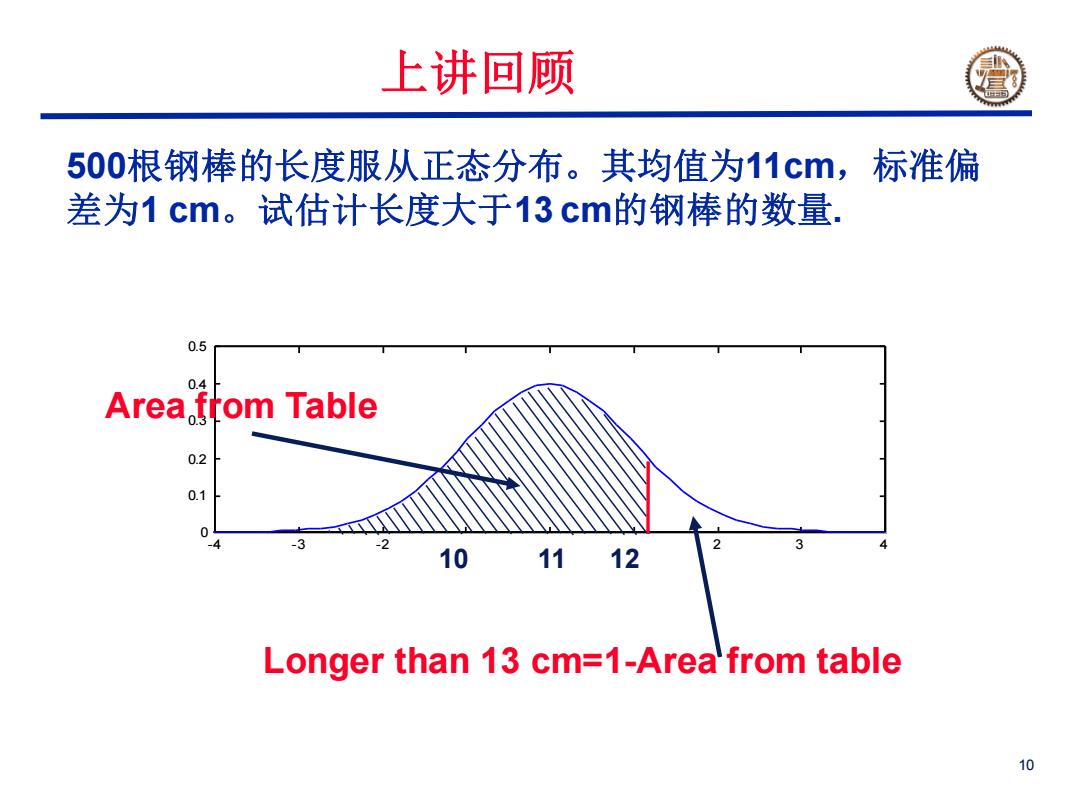
上讲回顾 500根钢棒的长度服从正态分布。其均值为11cm,标准偏 差为1cm。试估计长度大于13cm的钢棒的数量. 0.5 0.4 Area from Table 0.2 0.1 0 -3 10 1112 Longer than 13 cm=1-Area from table 10
10 500根钢棒的长度服从正态分布。其均值为11cm,标准偏 差为1 cm。试估计长度大于13 cm的钢棒的数量. -4 -3 -2 -1 0 1 2 3 4 0 0.1 0.2 0.3 0.4 0.5 10 11 12 Longer than 13 cm=1-Area from table Area from Table 上讲回顾