
试卷代号:1129 座位号 国家开放大学(中央广播电视大学)2015年春季学期“开放本科”期末考试 土木工程力学(本)试题(半开卷) 2015年7月 题 号 二 三 总 分 分 数 得 分 评卷人 一、单项选择题(每小题3分,共30分) 1,机动法作静定梁影响线的理论依据是( A.虚力原理 B.虚位移原理 C.位移互等定理 D.叠加原理 2.图示振动体系的自由度数目为( 2m A.1 E1=c∞ B.2 C.3 D.4 3.用位移法计算超静定刚架时,独立的结点角位移数等于()。 A.铰结点数 B.多余约束数 C.刚结点数 D.不确定 4,超静定结构在荷载作用下产生的内力与刚度()。 A.无关 B.相对值有关 C.绝对值有关 D.相对值绝对值都有关 482
试卷代号 :1129 座位号 国家开放大学(中央广播电视大学)2015 年春季学期"开放本科"期末考试 |得分|评卷人| | 土木工程力学(本) 试题(半开卷) |题号|一|二|三|总分| |分数 一、单项选择题{每小题 分,共 30 分} 1.机动法作静定梁影响线的理论依据是( )。 A. 虚力原理 B. 虚位移原理 c. 位移互等定理 D. 叠加原理 2. 图示振动体系的自由度数目为( )。 2015 A. 1 m @ 严立 B. 2 c. 3 D. 4 3. 用位移法计算超静定刚架时,独立的结点角位移数等于( )。 A. 伎结点数 B. 多余约束数 c. 刚结点数 D. 不确定 4. 超静定结构在荷载作用下产生的内力与刚度( )。 482 A. 元关 B.相对值有关 c.绝对值有关 D. 相对值绝对值都有关 2m @

5.位移法典型方程的物理意义是()。 A.附加约束上的平衡方程 B.附加约束上的位移条件 C.外力与内力的关系 D.反力互等定理 6.静定结构内力与反力影响线的形状特征是( )。 A.直线段组成 B.曲线段组成 C.直线曲线混合 D.变形体虚位移图 7.图乘法的适用条件为( )。 A.M,及M图中至少有一图是由直线组成 B.杆件EI为常量 C.杆件为直杆 D.同时满足以上条件 8.用力法求解图示结构时,基本未知量的个数是()。 A.4 B.5 C.6 D.7 2772 27 2 9.受弯杆件截面内力有()。 A.弯矩 B.剪力 C.轴力 D.以上三种 10.在力矩分配法中传递系数C与( )有关。 A.荷载 B.线刚度i C.近端支承 D.远端支承 483
5. 位移法典型方程的物理意义是( )。 A.附加约束上的平衡方程 B. 附加约束上的位移条件 c.外力与内力的关系 D. 反力互等定理 6. 静定结构内力与反力影响线的形状特征是( )。 A. 直线段组成 B.曲线段组成 c. 直线曲线混合 D. 变形体虚位移图 7. 图乘法的适用条件为( )。 A. 图中至少有一图是由直线组成 B. 杆件 EI 为常量 c.杆件为直杆 D. 同时满足以上条件 8. 用力法求解图示结构时,基本未知量的个数是( )。 A. 4 B. 5 c. 6 D. 7 9. 受弯杆件截面内力有( )。 A; 弯矩 c.轴力 10. 在力矩分配法中传递系数 与( A. 荷载 B. 线刚度 c. 近端支承 D. 远端支承 B. 剪力 D.以上三种 )有关。 483
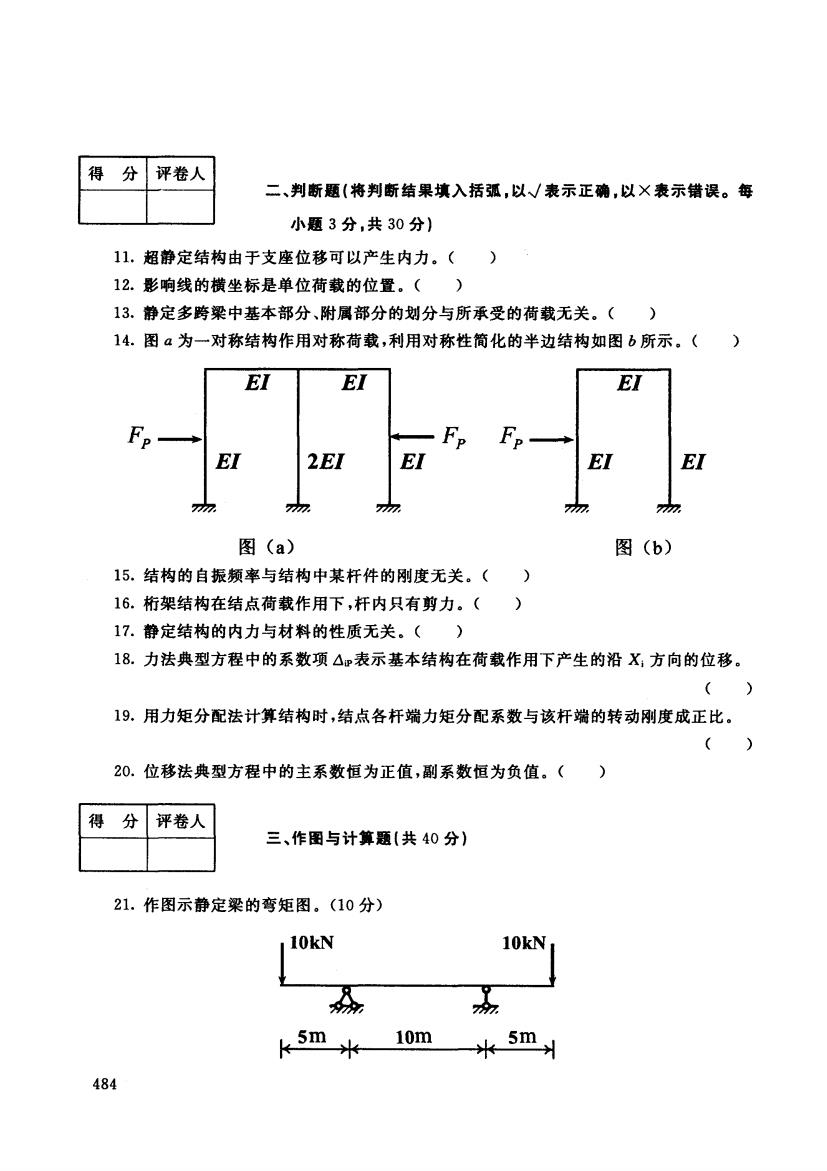
得 分 评卷人 二、判断题(将判断结果填入括孤,以√表示正确,以X表示错误。每 小题3分,共30分) 11.超静定结构由于支座位移可以产生内力。() 12.影响线的横坐标是单位荷载的位置。() 13.静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。() 14.图α为一对称结构作用对称荷载,利用对称性简化的半边结构如图b所示。() EI EI E Fp Fp Fp 2EI El EI 7 n 图(a) 图(b) 15。结构的自振频率与结构中某杆件的刚度无关。() 16.桁架结构在结点荷载作用下,杆内只有剪力。() 17.静定结构的内力与材料的性质无关。() 18.力法典型方程中的系数项△加表示基本结构在荷载作用下产生的沿X;方向的位移。 () 19.用力矩分配法计算结构时,结点各杆端力矩分配系数与该杆端的转动刚度成正比。 () 20.位移法典型方程中的主系数恒为正值,副系数恒为负值。() 得 分 评卷人 三、作图与计算题(共40分) 21.作图示静定梁的弯矩图。(10分) 10kN 10kN 9 k 5m 10m 5m 484
l~ 二、判断题{将判断结果填入括弧,以 表示正确,以×表示错误。每 小题 分,共 30 分) 1.超静定结构由于支座位移可以产生内力。( ) 12. 影响线的横坐标是单位荷载的位置。( ) 13. 静定多跨梁中基本部分、附属部分的划分与所承受的荷载元关。( ) 14. 为一对称结构作用对称荷载,利用对称性简化的半边结构如图 所示。( ) EI EI EI Fn---. P EI 2EI Fp .... EI EI (a) (b) 15. 结构的自振频率与结构中某杆件的刚度元关。( ) 16. 楠架结构在结点荷载作用下,杆内只有剪力。( ) 17. 静定结构的内力与材料的性质无关。( ) 18. 力法典型方程中的系数项.ðiP表示基本结构在荷载作用下产生的沿 方向的位移。 ( ) 19. 用力矩分配法计算结构时,结点各杆端力矩分配系数与该杆端的转动刚度成正比。 ( ) 20. 位移法典型方程中的主系数恒为正值,副系数恒为负值。( ) |得分|评卷人| | 三、作固与计算题{共 40 分} < N-7 nL -rm ,总 L5m.L 10m I~ .1 484
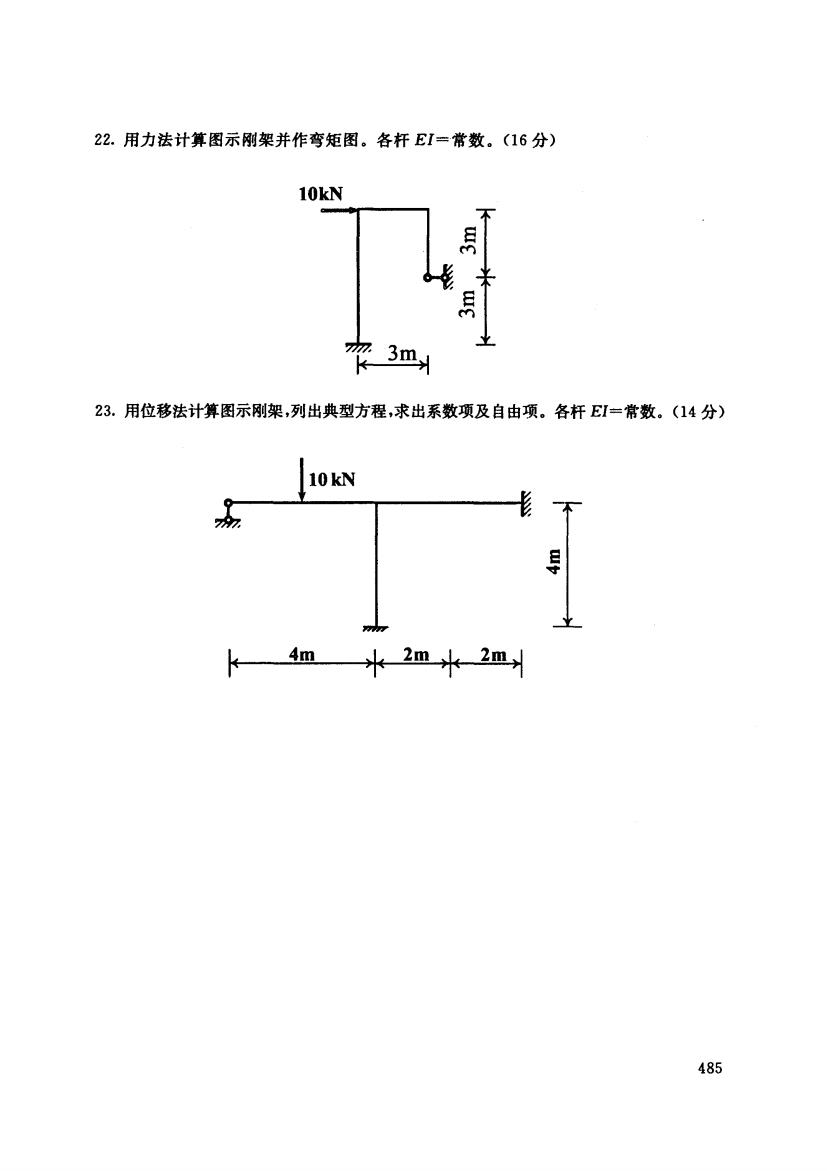
22.用力法计算图示刚架并作弯矩图。各杆EI=常数。(16分) 10kN 不 月 米 30% 23.用位移法计算图示刚架,列出典型方程,求出系数项及自由项。各杆EI=常数。(14分) 10kN 一不 4m22 485
22. 用力法计算图示刚架并作弯矩图。各杆 EI= 常数。(1 分〉 10kN g rη gmu 且叫 23. 用位移法计算图示刚架,列出典型方程,求出系数项及自由项.各杆 EI= 常数。(1 分〉 10 kN E 哩' 4m J~ 2m ‘ L 2m~1 485

试卷代号:1129 国家开放大学(中央广播电视大学)2015年春季学期“开放本科”期末考试 土木工程力学(本)试题答案及评分标准(半开卷) (供参考) 2015年7月 一、单项选择题(每小题3分,共30分) 1.B 2.A 3.C 4.B 5.A 6.A 7.D 8.C 9.D 10.D 一、判断题(将判断结果填入括弧,以√表示正确,以×表示错误。每小题3分,共30分) 11./ 12.√ 13.√ 14.× 15.× 16.× 17./ 18.√ 19./ 20.× 三、作图与计算题(共40分) 21.作图示静定梁的弯矩图。(10分) 10kN 10kN k5m 10m 5m 解: 50 kN-m 50kN-m A 22.用力法计算图示刚架并作弯矩图。各杆E1=常数。(16分) 10kN 不 3m 486
试卷代号 :1129 国家开放大学(中央广播电视大学 )2015 年春季学期"开放本科"期末考试 土木工程力学(本〉 试题答案及评分标准(半开卷) (供参考) 2015 一、单项选择题(每小题 分,共 30 分} 1. B 6.A 2.A 7.D 3. C 8.C 4. B 9.D 5.A 10. D 一、判断题{将判断结果填入括弧,以 表示正确,以×表示错误。每小题 分,共 30 分} 11. .J 12. .J 13. .J 14. X 15. X 16. X 17. .J 18. .J 19. .J 20. X 三、作固与计算题(共 40 分} 1.作图示静定梁的弯矩图。(1 分) AP 5m 10m 1< -'UA )1< )1< -'AU ~I 少乒 J;, 吧寸 AP 22. 用力法计算图示刚架并作弯矩图。各杆 EI= 常数。(1 分〉 10kN g 何飞 gmu 坦叶 486

解:结构是一次超静定结构,取基本体系如下图。 列力法方程611X1十△P=0 (2分) 作单位弯矩图M,图和荷载弯矩图Mp图。 3m 10kN 3m 13m =1 3m 7。 60kN宿 基本体系(2分) M,图(2分) M图(2分) u=2分).a,=-器2分) 将求出的系数和自由项代人力法方程,可求得X,=kN(2分) 用叠加原理作弯矩图 10 10 10 50 77 M图单位:(kN·m)(2分) 23.用位移法计算图示刚架,列出典型方程,求出系数项及自由项。各杆EI=常数。(14分) 10kN 4m水2m米2m 487
结构是一次超静定结构,取基本体系如下图。 列力法方程 11 .1 IP =O (2 分) 作单位弯矩图 图和荷载弯矩图 图。 3m 10kN 3m1 基本体系。分) (2 分) Mp (2 分) 811 =豆主EI'" (2 分):J.J ~ , ,.1UIP IP - 一旦旦EI (2 分) 将求出的系数和自由项代入力法方程,可求得 kN(2 分) 用叠加原理作弯矩图 10 50 图单位 (kN.m) (2 分) 23. 用位移法计算图示刚架,列出典型方程,求出系数项及自由项。各杆 EI= 常数。(1 分) 10 kN 4m J. 2m ~I. 2m 487

解:取基本体系如下图示 10 kN 知 基本体系(2分) 典型方程k1A1十F1n=0(2分) 令引-作风,图M图。 4=1 7.5 3i 2i 4i 6.25 2i M(3分) Mp单位:(kWm)(3分) 求得k11=11i(2分)Fp=7.5kN·m(2分) 488
取基本体系如下图示 基本体系。分) 典型方程是1l.1 1+F1P=Ü (2 分) <. i= 旦=旦,作 l 4 图、 图. 6.25 M1 (3 分) Mp 单位 CkN.m) c3分) 求得 ku =l1i (2 分) F 1P =7. 5kN. m (2 分〉 488