
6.线性支持向量机(线性SVM 口线性不可分情形下的广义最优线性分类面 第四章线性判别函数 。denotes+1 ■实际问题很少线性可分 denotes-1 虽然理论上可通过非线 性映射得到线性可分的 2009-11-10 数据,但如何获得这样 的映射,且避免过拟 合,是一个问题。 ■更实际的策略是允许一 定误差。 6.线性支持向量机(线性SVM④ 6.线性支持向量机(线性SV) 口线性不可分情形下的广义最优线性分类面 口线性不可分情形下的广义最优线性分类面 denotes+1 ■思路一:最小化Iw2 defoees1 ■思路二:同时最小 °denotes-1 的同时最小化错分训练 °.potesr1 化1w12和错分训练样 样本数目。 本到正确位置的距离。 minw+(#training errors) ■引入松弛项ξ: 折表参数 y(wx,+0)≥1-5 口问题:无法转化成二 次规划问题,优化很 i=1,,N, 困难;没有区分不同 5≥0. 误差的影响。 6.线性支持向量机(线性SVM 6.线性支持向量机(线性SV0 Soft margin SVM Soft margin SVM 折表参数,控制惩司错分样 太的程度:C越大,得罚越大 minf+) w,6, 5. y(w'x+o%)21-6, k为正整数是凸规划问题: 620,1=1…,N =1或2是二次规划问题: 仁」有较好的对偶形式。 Primal Lagrangian minL(w,m。,5.a,μ) Hard Margin(硬间隔) Soft Margin(软间隔) wf+c空 s1. 1,a≥0,4,20
第四章 线性判别函数 2009-11-10 2 6. 线性支持向量机 (线性SVM) 线性不可分情形下的广义最优线性分类面 实际问题很少线性可分。 虽然理论上可通过非线 性映射得到线性可分的 数据,但如何获得这样 的映射,且避免过拟 合,是一个问题。 更实际的策略是允许一 定误差。 denotes +1 denotes -1 3 6. 线性支持向量机 (线性SVM) 线性不可分情形下的广义最优线性分类面 思路一:最小化‖w‖2 的同时最小化错分训练 样本数目。 问题:无法转化成二 次规划问题,优化很 困难;没有区分不同 误差的影响。 denotes +1 denotes -1 min # training errors 2 w C 折衷参数 4 denotes +1 denotes -1 1 2 3 6. 线性支持向量机 (线性SVM) 线性不可分情形下的广义最优线性分类面 思路二:同时最小 化‖w‖2和错分训练样 本到正确位置的距离。 引入松弛项ξi denotes +1 denotes -1 0 ( )1 , 1,..., , 0. T ii i i y i N w x 5 6. 线性支持向量机 (线性SVM) Soft margin SVM 6 6. 线性支持向量机 (线性SVM) Soft margin SVM 0 2 1 , , 0 1 2 . . 1 , 0, 1, , ; min k N i i T ii i i C st y i N w w w x 2 0 1 0 1 1 : 1 min ( , , , , ) || || 2 ( )1 , .. , 0 Primal Lagrangi , . an 0 N i i N N T i i i i ii i i i i L C y st i w ξαμ w w x k为正整数是凸规划问题; k=1或2是二次规划问题; k=1有较好的对偶形式。 折衷参数,控制惩罚错分样 本的程度:C越大,惩罚越大

6.线性支持向量机(线性SVM 6.线性支持向量机(线性SVM Soft margin SVM 1. =w-之ayH=0 Soft margin SVM Ow .-之ay=0 aL ■约简KKT条件,可得对偶形式一二次规划问题 2. 80p 3. aL ag, C-a-4=0 min KKT conditions4. i=l 2台m y(w'x+)-1+≥0: 0≤a≤C,i=l,…,N; 5. 号≥0 s.t. 6. g20: 7. 4≥0 8 a(y(w'x,+0,)-1+5)=0 9. 45=0 6.线性支持向量机(线性SVM 6.线性支持向量机(线性SVM Soft margin SVM Soft margin SVM ■几何意义:超平面法向量是支持向量的线性组合。 ■几何意义 KKT complementarity conditions: y,(xw+b)>1g,=0 i:ay(wx,+)-(1-》=0 (C-a)5=0. =0for non-support vectors y,(x*w+b)1; 0<a,<C ■ a,=C→,(w'x,+o。)<1 12 6.线性支持向量机(线性SVM 6.线性支持向量机(线性SV) 口序贯最小优化(SMO)算法 口序贯最小优化(SMO)算法 ■无论Hard Margin或Soft Margin SVM,均可用 ■算法框架 经典的二次规划方法求解,但同时求解N个拉格 for =1:iter 朗日乘子涉及很多次迭代,计算开销太大,所以 a.根据预先设定的规则,从所有样本中选出两个 一般采用Sequential Minimal Optimization(SMO) b.保持其他拉格朗日乘子不变,更新所选样本对应的拉格 算法(.Plat,1999). 朗日乘子 end ■基本思路:每次只更新两个乘子,迭代获得最终 解。 ■优,点:只有两个变量的二次规划问题存在解析解。 ■关能技术细节: 口在每次迭代中,怎样更新乘子? 口怎么选择每次迭代需要更新的乘子?
7 6. 线性支持向量机 (线性SVM) Soft margin SVM 1 0 1 0 0 1. 0; 2. 0; 3. 0; 4. ( ) 1 0; 5. 0; 6. 0; 7. 0; 8. ( ) 1 0; 9. 0; KKT conditions N iii i N i i i i i i T ii i i i i T ii i i i i L y L y L C y y w x w w x w x 8 6. 线性支持向量机 (线性SVM) Soft margin SVM 约简 KKT 条件,可得对偶形式 — 二次规划问题 1 11 1 1 min ( ) ; 2 0 , 1, , ; . . 0. N NB T D i i ji ji j α i ij i N i i i L α αα y y α Ci N s t α y α x x 9 6. 线性支持向量机 (线性SVM) Soft margin SVM 几何意义:超平面法向量是支持向量的线性组合。 0 KKT complementarity conditions: : 1 0; ( ) 0. T ii i i i i i y C w x i = 0 for non-support vectors i 0 for support vectors 0 1 0 0 0 1; 0 1; . 1; i T N i ii iii T i i ii T i ii iii α C y α y α y α C y α y x w x w x w x w x x S V 10 6. 线性支持向量机 (线性SVM) Soft margin SVM 几何意义 11 6. 线性支持向量机 (线性SVM) 序贯最小优化 (SMO) 算法 无论 Hard Margin 或 Soft Margin SVM,均可用 经典的二次规划方法求解,但同时求解 N 个拉格 朗日乘子涉及很多次迭代,计算开销太大,所以 一般采用 Sequential Minimal Optimization (SMO) 算法 (J. Platt, 1999)。 基本思路:每次只更新两个乘子,迭代获得最终 解。 12 6. 线性支持向量机 (线性SVM) 序贯最小优化 (SMO) 算法 算法框架 优点:只有两个变量的二次规划问题存在解析解。 关键技术细节: 在每次迭代中,怎样更新乘子? 怎么选择每次迭代需要更新的乘子?

6.线性支持向量机(线性SVM① 6.线性支持向量机(线性SV① 口序贯最小优化(SMO)算法 口序贯最小优化(SMO)算法 ■假定在某一次迭代中,需更新样本【1,2对应的 ■约束的几何意义 拉格明日乘子a1,a %=C g:=C ■这个小规模的二次规划问题可以写成 化1=0 a=c L,@=a+a)广2++a 1=C =0 ay+a=ya a3=0 s1. 0≤a,≤C,i=1,2: 6.线性支持向量机(线性SVM① 6.线性支持向量机(线性SVM 口序贯最小优化(SMO)算法 口序贯最小优化(SMO)算法 ■更新拉格朗日乘子的步骤 ■更新拉格期日乘子的步骤 1.计算a,w的上下界L和H: 4.计算(剪辑)变量a2: L=max(0,ag-a),H=mim(C,C+ag-a),ify≠为 H,ifa≥H L=max(0.a+a-C).H=min(C.a+a )ify =y a={a,ifLsa≤H 2.计算Ls的二阶导数: L,ifa≤L =2xx2-xx-x2 5.更新a1 3.更新Ls asm=au(e-e) a=a+yy(da) e =g (x)-y 17 6.线性支持向量机(线性SVM 6.线性支持向量机(线性SVM0 口序贯最小优化(SMO)算法 口序贯最小优化(SMO)算法 ■选择需更新的乘子(启发式选择算法) ■由于所有乘子可分为三种情况,当还存在违反 口两个基本原则:(1)任何乘子必须满足KKT条 KKT条件的乘子时,在扫描时可忽略在0和C 件;(2)对一个不满足KKT圣件的乘子进行更 之间的乘子,以加速扫描进程。 新,应能最大限度增大目标函数的值(类似于梯 Training Set SMO Time PCG Time SMO PCG 度下降): Size (CPU sec)(CPU sec) Iterations Iterations 2477 26.3 64.9 10838 1888 口步骤:(1)先“扫描”所有乘子,把第一个(最)违 3H70 44.1 110.4 13975 2270 反KKT条件的作为更新对象,令其为a2;(②)在 4912 83.6 372.5 18978 5460 7366 156.7 545.4 27402 5274 所有不违反KKT条件的乘子中,选择使|日-e 9888 248.1 907.6 29751 5972 最大的对象,令其为a1 17188 581.0 3317.9 42020 9413 24692 1214.0 G659.7 55490 14H12 49749 3863.5 28877.6 93358 24235
13 6. 线性支持向量机 (线性SVM) 序贯最小优化 (SMO) 算法 假定在某一次迭代中,需更新样本 x1, x2 对应的 拉格朗日乘子α1, α2; 这个小规模的二次规划问题可以写成 1 2 2 1 2 111 2 2 2 , 3 11 2 2 1 1 2 2 3 1 max ( ) ( ) , 2 . . 0 , 1, ( 2 ) ; N S iii i N old old i i i i L yy y yy y y y s t C i k α xx x 常数 14 6. 线性支持向量机 (线性SVM) 序贯最小优化 (SMO) 算法 约束的几何意义 15 6. 线性支持向量机 (线性SVM) 序贯最小优化 (SMO) 算法 更新拉格朗日乘子的步骤 1. 计算 α2 new的上下界 L 和 H : 2. 计算 LS 的二阶导数: 3. 更新 LS: 12 11 2 2 2 TTT xx xx xx 16 序贯最小优化 (SMO) 算法 更新拉格朗日乘子的步骤 4. 计算(剪辑)变量α2 : 5. 更新α1 : 6. 线性支持向量机 (线性SVM) 17 6. 线性支持向量机 (线性SVM) 序贯最小优化 (SMO) 算法 选择需更新的乘子(启发式选择算法) 两个基本原则:(1) 任何乘子必须满足 KKT 条 件;(2) 对一个不满足 KKT 条件的乘子进行更 新,应能最大限度增大目标函数的值(类似于梯 度下降); 步骤: (1) 先“扫描”所有乘子,把第一个(最)违 反 KKT 条件的作为更新对象,令其为α2 ;(2) 在 所有不违反 KKT 条件的乘子中,选择使 最大的对象,令其为α1 。 | | 1 2 e e 18 6. 线性支持向量机 (线性SVM) 序贯最小优化 (SMO) 算法 由于所有乘子可分为三种情况,当还存在违反 KKT 条件的乘子时,在扫描时可忽略在 0 和 C 之间的乘子,以加速扫描进程
6.线性支持向量机(线性SVM① 总结:两类问题的线性判别函数 口总结 名称 准则 算法 ■目标:求对特征空间划分的最优超平面; Fisher wSW Jr(w)= w*=S(m1-m2) ■核心思想:最大化分类边界距离; S+5:wS,w ■支持向量:SVM的训练结果,在SVM分类决策 感知器 J(a)=∑(-a'y) ak+)=a(k)+r∑y 中起决定性作用。 veYe 口计算的复杂性取决于支持向量的数目,而不是样 最小错 本空间的维数,这在某种意义上避免了“维数灾难” 分样本 J(a)=(Ya-b)-Ya-b 共轭梯度法 口具有较好的“鲁棒”性:增、删非支持向量样本对模 MSE J,(a)=Ya-b a'=Y'b 型没有彩响;支持向量样本集具有一定的鲁棒性。 ■可保证解的全局最优性,不存在陷入局部极小解 SVM f+c() 二次规划 的问题。 st.constraints 2 7.多类问题(简介) 7.多类问题(简介) 口思路一:两类别问题可以推广到多类别问题 口思路二:多类线性判别函数(Linear Machine) ■0:/@法:将c类别问题化为(c-1)个两类(第i ■将特征空间确实划分为c个决策域,共有c个判 类与所有非类)问题,按两类问题确定其判别函 别函数 数与决策面方程。 8(x)=w,x+0o,i=1,,C ■ω:/0;法:将c类中的每两类别单独设计其线 ■决策规则: 性判别函数,总共有c(c1)2个线性判别函数. j=argmax g(x),i=1,....c; 阴影区域中的 ■决策域的边界由相邻决策域的判别函数共同决 点无法判定其 类别 定,此时应有g)厂gx: ■线性分类器的决策面是凸的,决策区域单连通: 非 ■多类分类器的分界面是分段线性的: 24 7.多类问题(简介) 7.多类问题(简介) 口多类线性决策面图例 口决策树:一种多级分类器,它采用分级的形式, 综合用多个决策规则,逐步把复杂的多类别分类 91>9 92>91 R 问题转化为若干个简单的分类问题来解决。 root Colo? level0 91>93 R R level I 9391 92>93 93>92 R
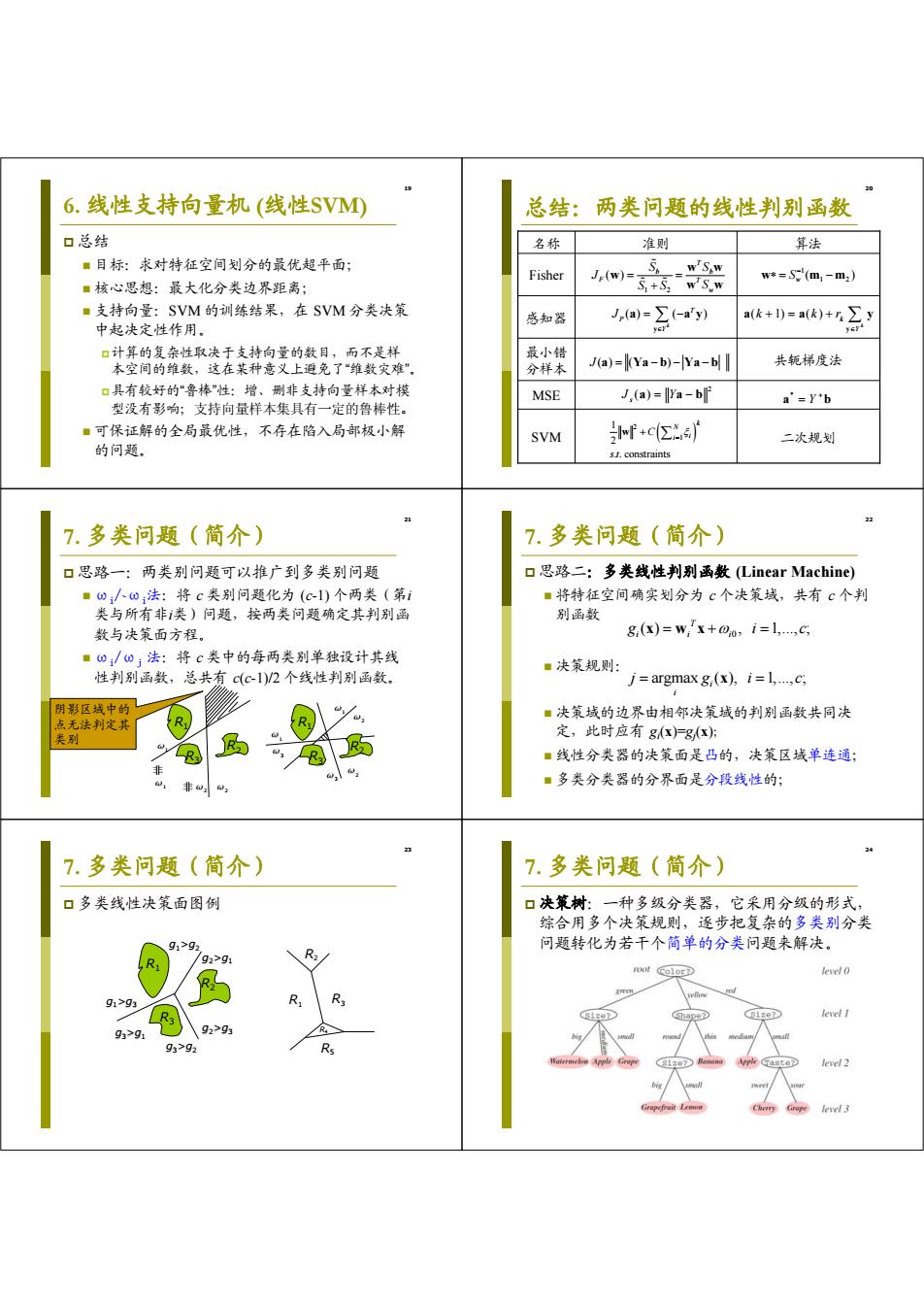
19 6. 线性支持向量机 (线性SVM) 总结 目标:求对特征空间划分的最优超平面; 核心思想:最大化分类边界距离; 支持向量:SVM 的训练结果,在 SVM 分类决策 中起决定性作用。 计算的复杂性取决于支持向量的数目,而不是样 本空间的维数,这在某种意义上避免了“维数灾难”。 具有较好的“鲁棒”性:增、删非支持向量样本对模 型没有影响;支持向量样本集具有一定的鲁棒性。 可保证解的全局最优性,不存在陷入局部极小解 的问题。 20 总结:两类问题的线性判别函数 MSE 共轭梯度法 最小错 分样本 SVM 二次规划 感知器 Fisher 名称 准则 算法 1 2 ( ) T b b F T w S S J S S S w w w w w 1 1 2 ( ) w S w mm () ( ) k T P Y J y a a y ( 1) ( ) k k Y k kr y a a y 2 ( ) s J Y a ab * Y a b J () ( ) a Ya b Ya b 2 1 1 2 . . constraints k N i i C s t w 21 7. 多类问题(简介) 思路一:两类别问题可以推广到多类别问题 ωi/~ωi法:将 c 类别问题化为 (c-1) 个两类(第i 类与所有非i类)问题,按两类问题确定其判别函 数与决策面方程。 ωi/ωj 法:将 c 类中的每两类别单独设计其线 性判别函数,总共有 c(c-1)/2 个线性判别函数。 R1 R3 ω1 R2 非 ω1 非ω2 ω2 R1 R3 R2 ω1 ω2 ω1 ω3 ω3 ω2 阴影区域中的 点无法判定其 类别 22 7. 多类问题(简介) 思路二:多类线性判别函数 (Linear Machine) 将特征空间确实划分为 c 个决策域,共有 c 个判 别函数 决策规则: 决策域的边界由相邻决策域的判别函数共同决 定,此时应有 gi (x)=gj (x); 线性分类器的决策面是凸的,决策区域单连通; 多类分类器的分界面是分段线性的; 0 ( ) , 1,..., ; T i ii g ic x wx argmax ( ), 1,..., ; i i j gi c x 23 7. 多类问题(简介) 多类线性决策面图例 R1 R3 R2 g1>g2 g1>g3 g3>g1 g3>g2 g2>g3 g2>g1 R1 R3 R2 R5 R4 24 7. 多类问题(简介) 决策树:一种多级分类器,它采用分级的形式, 综合用多个决策规则,逐步把复杂的多类别分类 问题转化为若干个简单的分类问题来解决
7.多类问题(简介) 7.多类问题(简介) 口二叉决策树 口二叉决策树 ■除叶节点外,决策树的每个节点m都有且只有 两个子节点nu和nm。 yes ■二叉决策树把复杂的多类别分类问题转化为多 级两类分类问题来解决。 aize.big? color yeliow ■在每个节点川,都把样本集分成两个子集。每 个子集可能仍包含多类别的样本,继续分直至 chape·round 01re。mai12 仅包含单类别样本的叶节点。 yes Cherry 27 总结:线性判别函数 口基于训练样本的直接确定判别函数方法主要包含 两个步骤: ■确定使用的判别函数类型或决策面方程类型,如 线性分类器,分段线性分类器等; ■在选定函数类型的条件下,确定相应的参数,从 而完成整个分类器设计; 口线性判别函数计算简单,在一定条件下能实现最 优分类,经常是一种“有限合理"的选择
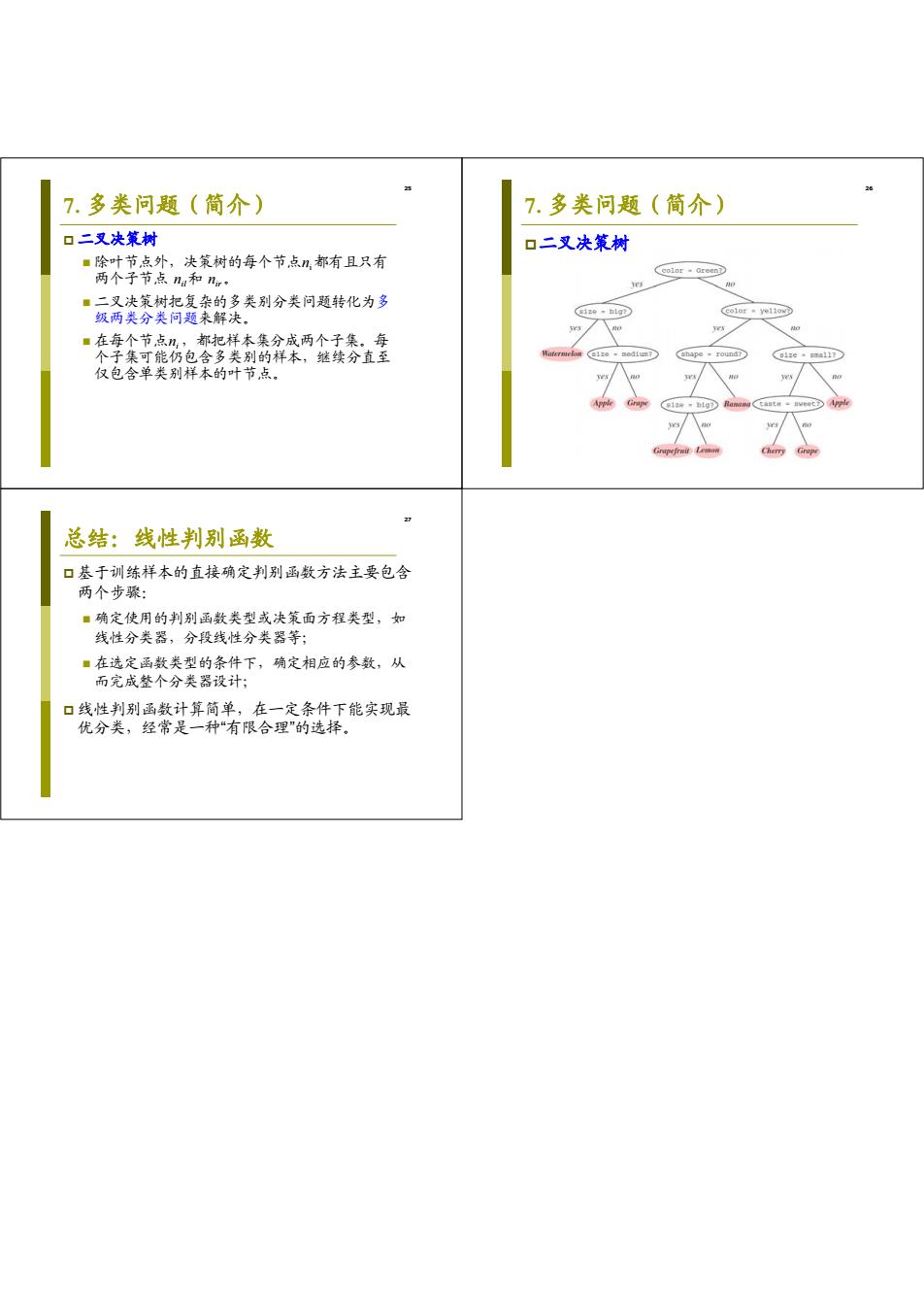
25 7. 多类问题(简介) 二叉决策树 除叶节点外,决策树的每个节点ni都有且只有 两个子节点 nil 和 nir。 二叉决策树把复杂的多类别分类问题转化为多 级两类分类问题来解决。 在每个节点ni ,都把样本集分成两个子集。每 个子集可能仍包含多类别的样本,继续分直至 仅包含单类别样本的叶节点。 26 7. 多类问题(简介) 二叉决策树 27 总结:线性判别函数 基于训练样本的直接确定判别函数方法主要包含 两个步骤: 确定使用的判别函数类型或决策面方程类型,如 线性分类器,分段线性分类器等; 在选定函数类型的条件下,确定相应的参数,从 而完成整个分类器设计; 线性判别函数计算简单,在一定条件下能实现最 优分类,经常是一种“有限合理”的选择