
9.0引言 第九章 口生物神经网络(biological neural network,BNN) 人工神经网络简介 2009-12-15 神经细胞) 生 物神 ell body Direction of message 凳 Axon 9.0引言 9.0引言 口人工神经网络(artificial neural network,.ANN) 口人工神经网络(artificial neural network,AN) ■由大量神经元经广泛互联组成的非线性网络(功 ■由大量神经元经广泛互联组成的非线性网络(功 能模块,数学模型); 能模块,数学模型): ■自底向上的综合方法:基本单元中功能模块中 ■自底向上的综合方法:基本单元一功能模块→ 系统。 神经元 系统。 ■三个要素 口神经元的计算特性(传递函数); 口网络的结构(连接形式); 口学习规则. 连接权垂 9.0引言 9.0引言 口人工神经网络发展历史简介 口神经网络的特,点 ■M-P神经元模型(MeCulloch&Pit1943) ■自学习 ■Hebb神经元学习准则(Hebb,1949) ■自适应 ■惑知机Perceptron(Rosenblatt 1958) ■并行处理 Adaline(Widrow and Hoff) ■分布表达与计算 ■《Perceptron》(Minsky&Papert,I969) 口神经网络的应用:NN本质上可以理解为函数逼 ■Hopfield模型(Hopfield,1982) 近,可以应用到众多领域 ■多层感知机MLP与反向传播算法BP(Rumelhart,. ■优化计算、信号处理、智能控制、模式识别、机 1986) 器视觉等
第九章 人工神经网络简介 2009-12-15 2 9.0 引言 生物神经网络 (biological neural network, BNN) 生物神经元(神经细胞)结构 3 9.0 引言 人工神经网络 (artificial neural network, ANN) 由大量神经元经广泛互联组成的非线性网络(功 能模块,数学模型); 自底向上的综合方法:基本单元 功能模块 系统。 4 9.0 引言 人工神经网络 (artificial neural network, ANN) 由大量神经元经广泛互联组成的非线性网络(功 能模块,数学模型); 自底向上的综合方法:基本单元 功能模块 系统。 三个要素 神经元的计算特性(传递函数); 网络的结构(连接形式); 学习规则。 5 9.0 引言 人工神经网络发展历史简介 M-P 神经元模型 (McCulloch & Pitts 1943) Hebb 神经元学习准则 (Hebb, 1949) 感知机 Perceptron (Rosenblatt 1958) Adaline (Widrow and Hoff) 《Perceptron》 (Minsky & Papert, 1969) Hopfield模型 (Hopfield,1982) 多层感知机 MLP 与反向传播算法 BP (Rumelhart, 1986) 6 9.0 引言 神经网络的特点 自学习 自适应 并行处理 分布表达与计算 神经网络的应用:NN 本质上可以理解为函数逼 近,可以应用到众多领域 优化计算、信号处理、智能控制、模式识别、机 器视觉等

8.1人工神经元 8.1人工神经元 口神经元模型(Neuron Model) 口神经网络示意困 ■多输入、单输出,带偏置; Layer 1 Layer 2 ■R个输入P,ER,即R维输 入向量P时 Input Neuron w Vector Input ■:网络输入,n=Wp+b DR个权值w,ER,即n维 af a 输入向量W: 口阀值b; ■输出:a=fWp+b) a=fWp+b) ai -fi(+bi) =P(LWa+b的 a1a (LWiza:+b) 口∫一输出/传递/激活函数. a:-D (Lwef (L.Wafl (TWup +bo)eh:)b) 8.1.1常用的输出函数 8.2神经网络的学习方法 口阙值函数 口神经网络的学习:从环境中获取知识并改进自身 性能,主要指调节网络参数使网络达到某种度 f(n)=hardlim(n)= 1(x≥0) 0(x<0) 量,又称为网络的训练; Hard-Lmit Functon 口学习方式: Purelin Transfer Function ■监督学习 f(n)=n ☑ ■非监督学习 ■再励学习 Sigmoid Function 口学习规则(learning rule): ■Hebb学习算法 1 f(n)= I+e-ri ■误差纠正学习算法 ■竞争学习算法 11 8.2.1学习方式 8.2.1学习方式 口监督学习 口非监督学习:不存在教 ■对训练样本集中的每一组输入能提供一组目标输 师,网络根据外部数据的 输入 出; 统计规律来调节系统参 环境 神经网络 ■网络根据目标输出与实际输出的误差信号来调节 数,以使网络输出能反映 网络参数。 数据的某种特性; t(n) 教师 期望输出 口再励学习:外部环境对网 输出 络输出只给出评价信息而 输入 非正确答案,网络通过强 环境 神经网络 实际输出 轴入 环境 化受奖励的动作来改善自 评价信息 神经网络 a(n) 比较 身的性能; p(n】 误差信号 e(n)
7 8.1 人工神经元 神经元模型 (Neuron Model) 多输入、单输出,带偏置; R 个输入 pi ∈R,即 R 维输 入向量 p; n:网络输入,n=W·p + b R 个权值 wi ∈R,即 n 维 输入向量 W; 阈值 b; 输出:a = f(W·p + b) f — 输出/传递/激活函数。 8 8.1 人工神经元 神经网络示意图 9 8.1.1 常用的输出函数 阈值函数 Purelin Transfer Function Sigmoid Function 1 ( 0) ( ) hardlim( ) ; 0 ( 0) x fn n x f () ; n n 1 () ; 1 n f n e 10 8.2 神经网络的学习方法 神经网络的学习:从环境中获取知识并改进自身 性能,主要指调节网络参数使网络达到某种度 量,又称为网络的训练; 学习方式: 监督学习 非监督学习 再励学习 学习规则 (learning rule): Hebb 学习算法 误差纠正学习算法 竞争学习算法 11 8.2.1 学习方式 监督学习 对训练样本集中的每一组输入能提供一组目标输 出; 网络根据目标输出与实际输出的误差信号来调节 网络参数。 教师 环境 神经网络 比较 实际输出 输入 期望输出 误差信号 p(n) t(n) a(n) e(n) 12 8.2.1 学习方式 非监督学习:不存在教 师,网络根据外部数据的 统计规律来调节系统参 数,以使网络输出能反映 数据的某种特性; 再励学习:外部环境对网 络输出只给出评价信息而 非正确答案,网络通过强 化受奖励的动作来改善自 身的性能; 环境 神经网络 输入 环境 神经网络 输入 输出 评价信息

8.2.2学习规则 8.2.2学习规则 口Hebb学习规则:如果神经元4,接收来自另一 口误差纠正学习 个神经元业,的输出,则当这两个神经元同时兴 ■基本思想:对于输出层第k个神经元,实际输 奋时,从到的权值”就得到加强。 出一a,目标输出一,误差信号一e(仁 a),则目标函数为基于误差信号e的函数,如 △wg=7aP, 学习 误差平方和判据(sum squared error,SSE),或均 ww+nap: 常数 方误差判据(mean squared error,MSE,即SSE对 所有样本的期望)。 ■几乎所有的神经网络学习算法可看成Hebb学习 规则的变形。 Jm[z]-[小 8.2.2学习规则 8.2.2学习规则 口误差纠正学习 口竞争学习 ■梯度下降法 ■输出神经元之间有侧向抑制性连接,较强单元获 △w=-nVJ; 胜并抑制其他单元,独处激活状态(Winner takes all,WTA)。 ■对于感知器和线形网络 △w与=n(P,-w)若神经元太获胜, △w与=IexP Aw与=0 若神经元k失败: Aw =nepT; delta学 习规则 ■对于多层感知器网络:扩展的delta学习规则, bp算法. 83前馈神经网络及其主要方法 8.3前馈神经网络及其主要方法 口前馈神经网络(feed forward NN):各神经元接受 口结构示意困 前一级输入,并输出到下一级,无反馈,可用一 Layer 3 有向无环图表示。 口前馈网络通常分为不同的层(layer),第i层的输 入只与第1层的输出联结。 + ■可见层:输入层(input layer)和输出层(output layer); a隐层(hidden layer):中间层。 -fi(Tup +b) a(LWuai+h) a (Lwua:+h) a-(TWup +b:)+b:)b)
13 8.2.2 学习规则 Hebb 学习规则:如果神经元 uj 接收来自另一 个神经元 ui 的输出,则当这两个神经元同时兴 奋时,从到的权值 wij 就得到加强。 几乎所有的神经网络学习算法可看成 Hebb 学习 规则的变形。 ( 1) ( ) , ; ij i n n ij ij i w ap w w ap 学习 常数 14 8.2.2 学习规则 误差纠正学习 基本思想:对于输出层第 k 个神经元,实际输 出 — ak ,目标输出 — tk ,误差信号 — ek (= tk – ak) ,则目标函数为基于误差信号 ek的函数,如 误差平方和判据 (sum squared error,SSE),或均 方误差判据 (mean squared error, MSE, 即 SSE 对 所有样本的期望)。 1 1 2 ; 2 2 T MSE k k J E eE e e 1 1 2 , 2 2 T SSE k k J e e e 15 8.2.2 学习规则 误差纠正学习 梯度下降法 对于感知器和线形网络 对于多层感知器网络:扩展的 delta 学习规则, bp 算法。 w J ; ; T w ep , w ep k j k j delta学 习规则 16 8.2.2 学习规则 竞争学习 输出神经元之间有侧向抑制性连接,较强单元获 胜并抑制其他单元,独处激活状态(Winner takes all, WTA)。 () 0 kj j kj k j w pw k w k 若神经元 获胜, 若神经元 失败; wkj k j 17 8.3 前馈神经网络及其主要方法 前馈神经网络 (feed forward NN):各神经元接受 前一级输入,并输出到下一级,无反馈,可用一 有向无环图表示。 前馈网络通常分为不同的层 (layer),第 i 层的输 入只与第 i-1 层的输出联结。 可见层:输入层 (input layer) 和输出层 (output layer); 隐层 (hidden layer) :中间层。 18 8.3 前馈神经网络及其主要方法 结构示意图
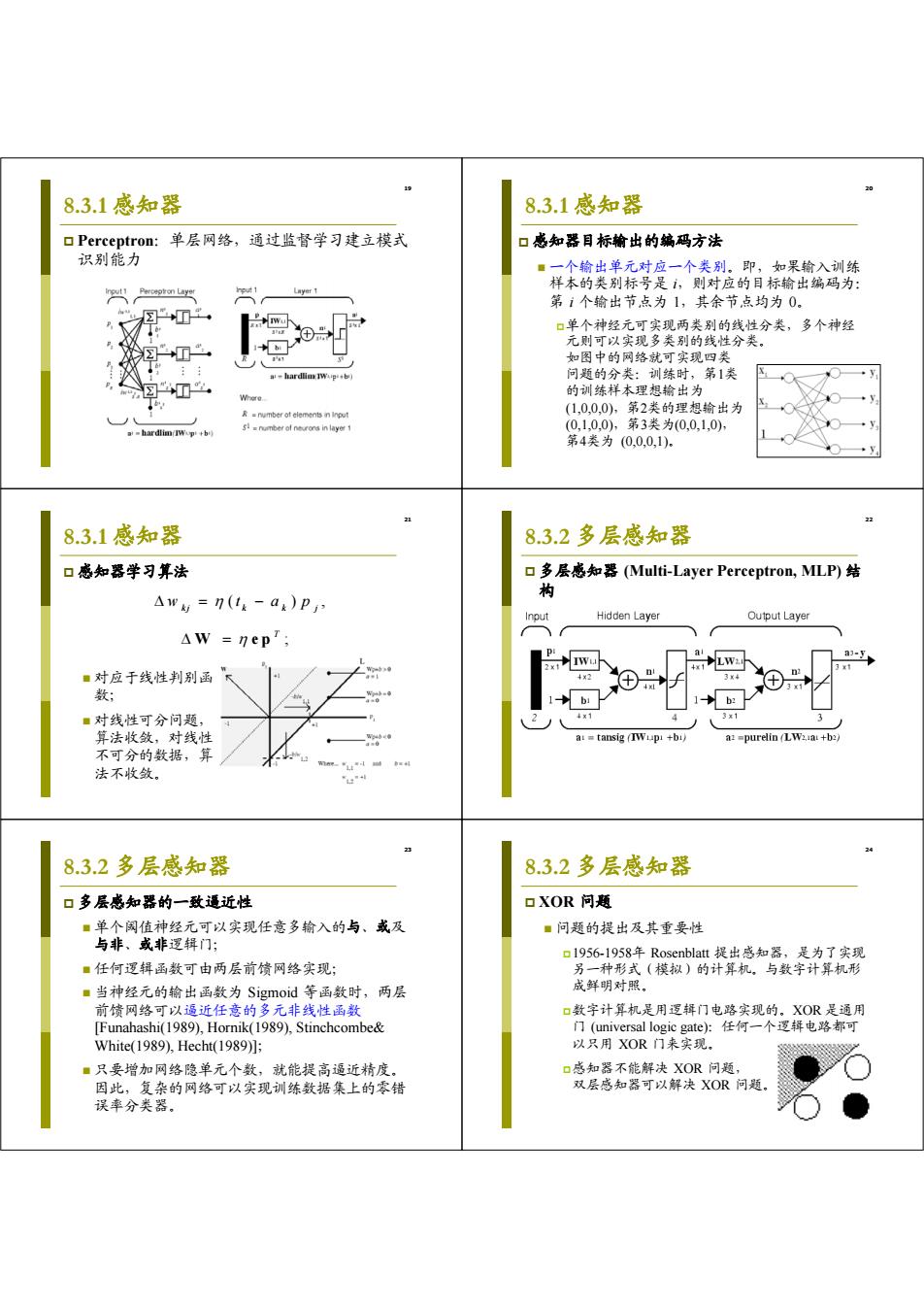
19 8.3.1感知器 8.3.1感知器 口Perceptron:单层网络,通过监督学习建立模式 口感知器目标输出的编码方法 识别能力 ■一个输出单元对应一个类别。即,如果输入训练 样本的类别标号是,则对应的目标输出编码为: 第1个输出节,点为1,其余节点均为0 口单个神经元可实现两类别的线性分类,多个神经 元则可以实现多类别的线性分类。 如图中的网络就可实现四类 -hard通IWug+b) 问题的分类:训练时,第1类 ☒ 的训练样本理想输出为 R-nmber ot elements n input (10,0,0),第2类的理想输出为 -hardlim IWop+b) (0,1,0,0),第3类为(0,0,1,0) 第4类为(00,0,1). 8.3.1感知器 8.3.2多层感知器 口感知器学习算法 口多层感知器(Multi-.Layer Perceptron,MLP)结 构 △w=n(1k-ak)P Input Hidden Layer Output Layer AW =nep'; LW: a-Ep ■对应于线性判别函 34 数; b: ■对线性可分问题, 3x1 算法收敛,对线性 a:tansig (+bi a:=purelin (LW2a +b2) 不可分的数据,算 法不收敛。 2布 8.3.2多层感知器 8.3.2多层感知器 口多层感知器的一致逼近性 口XOR问题 ■单个闲值神经元可以实现任意多输入的与、或及 ■问题的提出及其重要性 与非、或非逻辑门; 口1956-1958年Rosenblatt提出感知器,是为了实现 ■任何逻辑函数可由两层前馈网络实现; 另一种形式(模拟)的计算机。与数字计算机形 ■当神经元的输出函数为Sigmoid等函数时,两层 成鲜明对照。 前馈网络可以逼近任意的多元非线性函数 口数字计算机是用逻辑门电路实现的。XOR是通用 [Funahashi(1989),Hornik(1989),Stinchcombe& 门(universal logic gate)任何一个逻辑电路都可 White(1989),Hecht(1989)]; 以只用XOR门来实现. ■只要增加网络隐单元个数,就能提高逼近精度。 口感知器不能解决XOR问题, 因此,复杂的网络可以实现训练数据集上的零错 双层感知器可以解决XOR问题 误率分类器
19 8.3.1 感知器 Perceptron:单层网络,通过监督学习建立模式 识别能力 20 8.3.1 感知器 感知器目标输出的编码方法 一个输出单元对应一个类别。即,如果输入训练 样本的类别标号是 i,则对应的目标输出编码为: 第 i 个输出节点为 1,其余节点均为 0。 单个神经元可实现两类别的线性分类,多个神经 元则可以实现多类别的线性分类。 如图中的网络就可实现四类 问题的分类:训练时,第1类 的训练样本理想输出为 (1,0,0,0),第2类的理想输出为 (0,1,0,0),第3类为(0,0,1,0), 第4类为 (0,0,0,1)。 21 8.3.1 感知器 感知器学习算法 对应于线性判别函 数; 对线性可分问题, 算法收敛,对线性 不可分的数据,算 法不收敛。 ( ), w t ap kj k k j ; T W ep 22 8.3.2 多层感知器 多层感知器 (Multi-Layer Perceptron, MLP) 结 构 23 8.3.2 多层感知器 多层感知器的一致逼近性 单个阈值神经元可以实现任意多输入的与、或及 与非、或非逻辑门; 任何逻辑函数可由两层前馈网络实现; 当神经元的输出函数为 Sigmoid 等函数时,两层 前馈网络可以逼近任意的多元非线性函数 [Funahashi(1989), Hornik(1989), Stinchcombe& White(1989), Hecht(1989)]; 只要增加网络隐单元个数,就能提高逼近精度。 因此,复杂的网络可以实现训练数据集上的零错 误率分类器。 24 8.3.2 多层感知器 XOR 问题 问题的提出及其重要性 1956-1958年 Rosenblatt 提出感知器,是为了实现 另一种形式(模拟)的计算机。与数字计算机形 成鲜明对照。 数字计算机是用逻辑门电路实现的。XOR 是通用 门 (universal logic gate):任何一个逻辑电路都可 以只用 XOR 门来实现。 感知器不能解决 XOR 问题, 双层感知器可以解决 XOR 问题
8.3.2多层感知器 8.3.3反向传播(BP)算法 口XOR问题 口训练问题:多层感知器的中间隐层不直接与外界 连接,其误差无法直接计算。 口反向传播(Back propagation)算法:从后向前 (反向)逐层“传播”输出层的误差,以间接算出 隐层误差。分两个阶段: ■正向过程:从输入层经隐层逐层正向计算各单元 的输出; ■反向过程:由输出层误差逐层反向计算隐层各单 元的误差,并用此误差修正前层的权值。 8.3.3反向传播(BP)算法 8.3.3反向传播(BP)算法 口反向传播算法是一种通过迭代求优化解的方法。 口正向过程 ■目标:使输出与输入之间的实际映射关系与所期 望的映射关系一致。 a=∫(n),n}=w.a-=∑w'a- ■基本思想: 口设计一个代价函数作为选代学习过程的目标函 数: 口利用代价函数对各参数的偏导数来确定各参数的 修正量; 口利用网络计算的分层结构导出计算的分层表示函 数,简化导数计算。 :-FLwua+b) 20 8.3.3反向传播(BP)算法 8.3.3反向传播(BP)算法 口目标函数:sum squared error,SSE 口输出层的权值修正 JSSE 1 9(t,-a)2; 0J ssE=o ssEuL=-(1-a )f'(n da,onj 扩展de1t& 口权值修正:梯度下降法 △w,=n(t,-a,)f'(n,)a-) 学习规则 。权值修正量 ■当输出函数是Sigmoid函数: △w,=-1 0J ssE=-n- 0J ssE on aw j an,ow a-fa)=1+2fa)aty=a0-ah e-9 =- 0J ssE a(k-1) △w,=7(t,-a,)a,(l-a,)a- 「向部梯度
25 8.3.2 多层感知器 XOR 问题 26 8.3.3 反向传播 (BP) 算法 训练问题:多层感知器的中间隐层不直接与外界 连接,其误差无法直接计算。 反向传播 (Back propagation) 算法:从后向前 (反向)逐层“传播”输出层的误差,以间接算出 隐层误差。分两个阶段: 正向过程:从输入层经隐层逐层正向计算各单元 的输出; 反向过程:由输出层误差逐层反向计算隐层各单 元的误差,并用此误差修正前层的权值。 27 8.3.3 反向传播 (BP) 算法 反向传播算法是一种通过迭代求优化解的方法。 目标:使输出与输入之间的实际映射关系与所期 望的映射关系一致。 基本思想: 设计一个代价函数作为迭代学习过程的目标函 数; 利用代价函数对各参数的偏导数来确定各参数的 修正量; 利用网络计算的分层结构导出计算的分层表示函 数,简化导数计算。 28 8.3.3 反向传播 (BP) 算法 正向过程 ( ) ( ) ( ) ( ) ( 1) ( ) ( 1) ( ), ; k k k k k kk j j j j ij i i a fn n w a w a 29 ( 1) ( 1) . SSE SSE j j j jj SSE k k j j J J n n J n w w w a a 8.3.3 反向传播 (BP) 算法 目标函数:sum squared error, SSE 权值修正:梯度下降法 权值修正量 1 2 ( ); 2 S SSE j j j J ta S 局部梯度 30 8.3.3 反向传播 (BP) 算法 输出层的权值修正 当输出函数是 Sigmoid 函数: ' ' ( 1) ( ) ( ), ( )() . SSE SSE j j jj j j jj k j jj j J J a t a fn n an t a fn w a ' 2 ( 1) 1 ( ) ( ) (1 ) 1 (1 ) ( ) (1 ) n n n k j j jj j e a f n f n aa e e t aa a w a , ; 扩展delta 学习规则

8.3.3反向传播(BP)算法 8.3.3反向传播(BP)算法 口隐层的权值修正:局部梯度(误差)的反向传播 口 算法步骤 6,=E 后层的全部单元都受的影响 1. 初始值选择W(O) 0 2. 前向计算,求出所有神经元的输出a,(1): 3. 对输出层计算δ:6,=(t,-a,)a,(1-a, on, 4.从后向前计算各隐层δ:δ,=a,I-a,)∑wn8 =∑6,wf'(n 5. 计算并保存各权值修正量:△wy=-n8,a Cw06 6.修正权值:"y(1+1)=Py(t)+△w 6 7. 判断是否收敛,如收敛则结束,否则转至Step2. 8.3.3反向传播(BP)算法 8.3.3反向传播(BP)算法 口设计讨论 口讨论:MLPs的过拟合现象 ■两层感知器可以逼近任意的多元非线性函数; ■增加隐单元个数→训练数据分类正确率提高, ■输入层单元数=输入变量Or特征维数; ■训练数据分类正确率提高?一测试数据正确率 ■输出层单元数=模式类数Or待逼近的函数个数; 提高。 ■隐层单元数:无有效选择方法 ■识别正确率与隐单元个数有很大关系! ■网络初始化对结果有影响,常用较小的随机数: 过合 ■学习率n的选择:可在(0.1,3)试探: ■增加惯性项的BP算法: 料者 △wy(t)=-1δ,a,+a△wy(t-1) 1国0天个金 26 8.3.3反向传播(BP)算法 8.3.3反向传播(BP)算法 口多层感知器和Bayes决策的关系 口多层感知器和Bayes决策的关系 与W无关 ■对于两类问题{0,1},采用均方误差训练,且神 经元输出函数为Sigmoid函数时,多层感知器的 p(xIo,)=P(x)p(@,lx) P(0,) 输出是对Bayes后验概率的最小均方误差估计. p(x)=P(@,)p(o,Ix)+P(o:)mo2Ix); 1 E,w)=N三/,w)-d(I E,(w)之∫【fx,w)-p(o,Ix川p)dsP(e,1sI-p(e,1s》Px)ds [Σw-r]0[Σr] =e(w)+p(@,Ix)(I-p(@,lx))p(x)d P(@:)J[f(x,w)-1]p(xl@,)dx e(w)=JIf(x.w)-p(o,Ix)]p(x)dx, 均方逼 近误差 大数定理 +P(@2)J[f(x,w)Jp(xI@:)dx; N-→o
31 8.3.3 反向传播 (BP) 算法 隐层的权值修正:局部梯度(误差)的反向传播 ( 1) ' ( 1) ' ( 1) ( ), ( ( )) ; SSE j j k SSE i j i i jj i ji j i k j j k i ji j i J n J n a n an wfn wfn w a a wji i nj aj ni δj wji δi 后层的全部单元都受nj 的影响 32 8.3.3 反向传播 (BP) 算法 算法步骤 1. 初始值选择 W(0); 2. 前向计算,求出所有神经元的输出 3. 对输出层计算δ: 4. 从后向前计算各隐层δ: 5. 计算并保存各权值修正量: 6. 修正权值: 7. 判断是否收敛,如收敛则结束,否则转至Step 2。 ( ); j a t ( ) (1 ); j j jj j t aa a (1 ) ; j j j ji i i aaw ; w a ij j i ( 1) ( ) ; wt wt w ij ij ij 33 8.3.3 反向传播 (BP) 算法 设计讨论 两层感知器可以逼近任意的多元非线性函数; 输入层单元数=输入变量 or 特征维数; 输出层单元数=模式类数 or 待逼近的函数个数; 隐层单元数:无有效选择方法 网络初始化对结果有影响,常用较小的随机数; 学习率η的选择: 可在 (0.1, 3) 试探; 增加惯性项的 BP 算法: ( ) ( 1). wt a wt ij j i ij 34 8.3.3 反向传播 (BP) 算法 讨论:MLPs 的过拟合现象 增加隐单元个数 训练数据分类正确率提高。 训练数据分类正确率提高 测试数据正确率 提高。 识别正确率与隐单元个数有很大关系! 35 8.3.3 反向传播 (BP) 算法 多层感知器和 Bayes 决策的关系 对于两类问题 {0,1},采用均方误差训练,且神 经元输出函数为 Sigmoid 函数时,多层感知器的 输出是对 Bayes 后验概率的最小均方误差估计。 1 2 2 2 1 2 1 2 2 2 1 1 2 2 2 1 1 [ ( , ) 1] [ ( , )] 1 [ ( , ) ( )] ( ) [ ( , ) 1] ( | ) ( ) [ ( , )] ( | ) ; ( ) K K K s N N f f NN NN f d N Pf pd Pf pd E x x x xw xw xw x xw x x xw x x w 大数定理, N∞ 36 8.3.3 反向传播 (BP) 算法 多层感知器和 Bayes 决策的关系 2 1 1 1 2 1 1 ( ) [ ( , ) ( | )] ( ) ( | )(1 ( | )) ( ) ( ) ( | )(1 ( | )) ( ) s E f p pd p p pd e p p pd w xw x x x x x x x w x x xx 2 argm in ( ) argm in ( ) E e a w w 2 2 1 2 ( ) [ ( , ) ( | )] ( ) argm in ( ) argm in , ( ). s e fp E d e p w xw x x x w w 1 1 1 11 2 2 () ( | ) (| ) , ( ) ( ) ( ) ( | ) ( ) ( | ); p p p P p Pp P p x x x xx x 且 与w无关 均方逼 近误差

8.3.4径向基函数网络 8.3.4径向基函数网络 口径向基函数网络 口结构示意困 ■只有一个隐层,隐层单元采用径向基函数: fs)=2w,-nD,x∈R ■输出为隐层的线性加权求和; ■径向基函数(radial basis function,RBF):径向对 称的标量函数p(-μD,最常用的RBF是高斯 核函数 H.. 0 (r)=exp(- 8.3.4径向基函数网络 8.3.4径向基函数网络 口RBF网络的作用 口参数估计 ■可看成对未知函数的逼近器,相当于用基函数的 ■可调参数 加权和来实现对函数的逼近。 口隐单元的个数m需要事先确定; aRBF网络的一致逼近性能与MLPs一样,可以一 口隐单元基函数参数:,i=l,2,…,m 致逼近闭区间上的任意连续函数, 口输出层权值:",i=1,2,…,m ■隐层把原始的非线性可分的特征空间变换到另一 ■估计方法: 个空间(通常是高维空间),使之可以线性可分。 口聚类的方法估计, ■用于模式识别的RBF网络等价于首先应用非参 口LMS估计: 数方法估计出概率密度,然后进行分类。 8.4神经网络模式识别典型方法 8.4神经网络模式识别典型方法 口MLP是模式识别中应用最多的的网络模型; 口ACON应用典型方法 口两种拓扑结构: ■网络的每个输入节点对应于样本的一个特征: ■ACON:all classes one net,多输出型 ■输出层单元采用“℃中取1”编码方式,每个输出节 OCON:one class one net,单输出型 点对应一个类别,即输出层单元数=模式类数: 口训练样本数据的期望输出:[0,0,,1,,0],即其 所属类的相应输出节点为1,其他节点均为0: 0 口识别阶段:未知样本的类别判定为与输出值最大 的节点对应的类别。 ACON OCON
37 8.3.4 径向基函数网络 径向基函数网络 只有一个隐层,隐层单元采用径向基函数; 输出为隐层的线性加权求和; 径向基函数 (radial basis function, RBF):径向对 称的标量函数 φ(||x-μ||),最常用的 RBF 是高斯 核函数 2 ( ) exp( ). 2 r r 38 8.3.4 径向基函数网络 结构示意图 ( ) ( ), m d ii i i f x x w R μ x 39 8.3.4 径向基函数网络 RBF 网络的作用 可看成对未知函数的逼近器,相当于用基函数的 加权和来实现对函数的逼近。 RBF 网络的一致逼近性能与 MLPs 一样,可以一 致逼近闭区间上的任意连续函数。 隐层把原始的非线性可分的特征空间变换到另一 个空间(通常是高维空间),使之可以线性可分。 用于模式识别的 RBF 网络等价于首先应用非参 数方法估计出概率密度,然后进行分类。 40 8.3.4 径向基函数网络 参数估计 可调参数 隐单元的个数 m 需要事先确定; 隐单元基函数参数: 输出层权值: 估计方法: 聚类的方法估计 LMS 估计 , ,i 1,2, ,m; μi i , 1,2, , ; wi m i , ; i i μ ; wi 41 8.4 神经网络模式识别典型方法 MLP 是模式识别中应用最多的的网络模型; 两种拓扑结构: ACON: all classes one net,多输出型 OCON: one class one net,单输出型 ACON OCON 42 8.4 神经网络模式识别典型方法 ACON 应用典型方法 网络的每个输入节点对应于样本的一个特征; 输出层单元采用 “c中取1” 编码方式,每个输出节 点对应一个类别,即输出层单元数=模式类数; 训练样本数据的期望输出:[0, 0,…, 1,…, 0],即其 所属类的相应输出节点为1,其他节点均为0; 识别阶段:未知样本的类别判定为与输出值最大 的节点对应的类别

8.4神经网络模式识别典型方法 口前馈神经网络与统计模式识别在方法上具有一定 的等价关系: ■单层感知器一线性分类器 ■多层感知器一非线性分类器 ·径向基函数网络一Parzen窗密度估计分类器 口多层感知器集特征提取与分类于一体: ■隐层进行非线性特征提取,将输入空间变换到隐 层输出空间,使样本在此空间具有最好的可分性 ■输出层进行分类决策(有时仅需线性分类)
43 8.4 神经网络模式识别典型方法 前馈神经网络与统计模式识别在方法上具有一定 的等价关系: 单层感知器 — 线性分类器 多层感知器 — 非线性分类器 径向基函数网络 — Parzen 窗密度估计分类器 多层感知器集特征提取与分类于一体: 隐层进行非线性特征提取,将输入空间变换到隐 层输出空间,使样本在此空间具有最好的可分性。 输出层进行分类决策(有时仅需线性分类)