
5.1分段线性判别函数 口对实际的模式识别问题来说,各类在特征空间中 的分布往往比较复杂,采用线性判别函数无法取 第五章非线性判别函数 得满意的分类效果,可以采用分段线性判别或二 次函数判别等方法,是最为简单的形式。 2009-11-10 ■分段战性判别函数:一种特殊的非线性判别函 数,它的决策面是若千超平面。 ■树分类器的各节点上采用线性判别规则,即构成 分段线性分类器。 5.1分段线性判别函数 5.1分段线性判别函数 口对实际的模式识别问题来说,各类在特征空间中 口分段段数问题 的分布往往比较复杂,采用线性判别函数无法取 ■与样本集分布有关:分段段数过少,其分类效果 得满意的分类效果,可以采用分段线性判别或二 必然要差:但段数又要尽可能少,以免分类判别 次函数判别等方法,是最为简单的形式。 函数过于复杂,增加分类决策的计算量。 ■实际问题中,同一类样本的子类的数目就可作为 确定分段段数的依据。但多数情况下样本分布及 合适子类划分并不知道,聚类的方法将样本划分 成相对密集的子类,然后用各种方法设计各段判 别函数。 I:线性判别 1:分段线性判别 ■这一章主要讨论在样本分布及子类划分大体已定 Ⅲ:二次判别 的情况下,设计分段线性判别函数的问题。 5.1分段线性判别函数 5.1分段线性判别函数 口形式定义 口形式定义 ■设每个类由若千个子类组成,即 ■定义ω,类的判别函数 o={包,2,…,} 8,(x)=maxg(), 1=2 其中1为⊙,类所有子类的个数。 ■决策规则 ■对每个子类定义一个线性判别函数 8,)=max8(则k∈o g(x)=wx+00,1=1,2,l,i=1,2c ■决策面取决于相邻的决策域:如果第i类的第n 其中g表示ω,类第I段的线性判别函数,w,/与 个子类与第j类的第m个子类相邻,则由它们共 0。分别是第1段的权向量与阅值权。 同决定的决策面方程是 8(x)=8"(x)
第五章 非线性判别函数 2009-11-10 2 5.1 分段线性判别函数 对实际的模式识别问题来说,各类在特征空间中 的分布往往比较复杂,采用线性判别函数无法取 得满意的分类效果,可以采用分段线性判别或二 次函数判别等方法,是最为简单的形式 。 分段线性判别函数:一种特殊的非线性判别函 数,它的决策面是若干超平面。 树分类器的各节点上采用线性判别规则,即构成 分段线性分类器。 3 5.1 分段线性判别函数 对实际的模式识别问题来说,各类在特征空间中 的分布往往比较复杂,采用线性判别函数无法取 得满意的分类效果,可以采用分段线性判别或二 次函数判别等方法,是最为简单的形式 。 R1 R3 R2 II I: 线性判别 II:分段线性判别 III: 二次判别 I III 4 5.1 分段线性判别函数 分段段数问题 与样本集分布有关:分段段数过少,其分类效果 必然要差;但段数又要尽可能少,以免分类判别 函数过于复杂,增加分类决策的计算量。 实际问题中,同一类样本的子类的数目就可作为 确定分段段数的依据。但多数情况下样本分布及 合适子类划分并不知道,聚类的方法将样本划分 成相对密集的子类,然后用各种方法设计各段判 别函数。 这一章主要讨论在样本分布及子类划分大体已定 的情况下,设计分段线性判别函数的问题。 5 5.1 分段线性判别函数 形式定义 设每个类由若干个子类组成,即 其中 l i 为 ωi 类所有子类的个数。 对每个子类定义一个线性判别函数 其中 gi l 表示ωi 类第 l 段的线性判别函数,wi l 与 ωi0 l 分别是第 l 段的权向量与阈值权。 0 ( ) , 1,2,..., , 1,2... ; T l ll i ii i g l li c x wx , , , ; 1 2 il i i i i 6 5.1 分段线性判别函数 形式定义 定义ωi 类的判别函数 决策规则 决策面取决于相邻的决策域:如果第 i 类的第 n 个子类与第 j 类的第 m 个子类相邻,则由它们共 同决定的决策面方程是 1,2,..., ( ) max ( ), i l i i l l g g x x 1,2,..., ( ) max ( ), ; j ij i c g g x xx 则 ( ) ( ). n m i j g g x x
5.2基于距离的分段线性判别函数 5.2基于距离的分段线性判别函数 口回顾最小距离分类器:第二章曾讨论过正态分布 口按距离分类的原理可以推广,即把各类别样本特 条件下,两类别问题在各特征统计独立、同方 征向量的均值作为各类的代表,点(prototype), 差、且先验概率相等情况下,最小错误率贝叶 而样本的类别按它到各类别代表点的最小距离划 斯决策就是最小距离决策,即 分;决策面是两类别均值连线的垂直平分面。 ‖x-4lp-x-μP0 xE02 附近时才有效 其中μ,与μ2为各类的均值。 ■否则只有将各类别划分成相对密集的子类,每个 子类以它们的均值作为代表点,然后按最小距离 分类。 =0 5.2基于距离的分段线性判别函数 5.2基于距离的分段线性判别函数 口分段线性距离分类器 ■判别函数:如果对于⊙,类有1个子类,则有1个 代表点,或者说把属于⊙,的决策域R分成I个 子域;对于每个子区域R的均值用m,表示,并 以此作为该子区域的代表点,则判别函数定义为: 1:线性距离列蹦 :分我线性更离列划 8,(=典‖x-m ■判决规则 最小距离分类器 ifg,☒=min8,()then xe, 多个最小距高分类器组成 不适用的情况 分受战性分类面 12 5.3错误修正算法 5.3错误修正算法 口aTy:是增广权向量a,与规范化的增广样本向量 口条件:已知每类的子类数目1,但子类划分情况 y的点积(内积)。内积值比较大则表示这两个 未知。 向量在方向上比较一致,即向量间的夹角较小。 口基本思略:可假设初始权向量,然后由训练样本 口如果某一类样本比较分散,但是能用若干个增广 提供的错误信息进行迭代修正,直至收敛。 权向量a表示,使得同一类样本y能够做到与 代表自己一类的a:的内积(aTy)的最大值大于与 口算法步骤 代表其它类的增广权向量的内积值,则可以做到 1.初始化:任意给定各子类的权向量: 正确分类。因此这种算法就是要利用错误提供的 信息进行迭代修正。(类似于多类线性判别函数 a0),il,2,…,c,1=1,2,…,6 的固定增量算法。) 其中括号中的数目表示迭代的次数
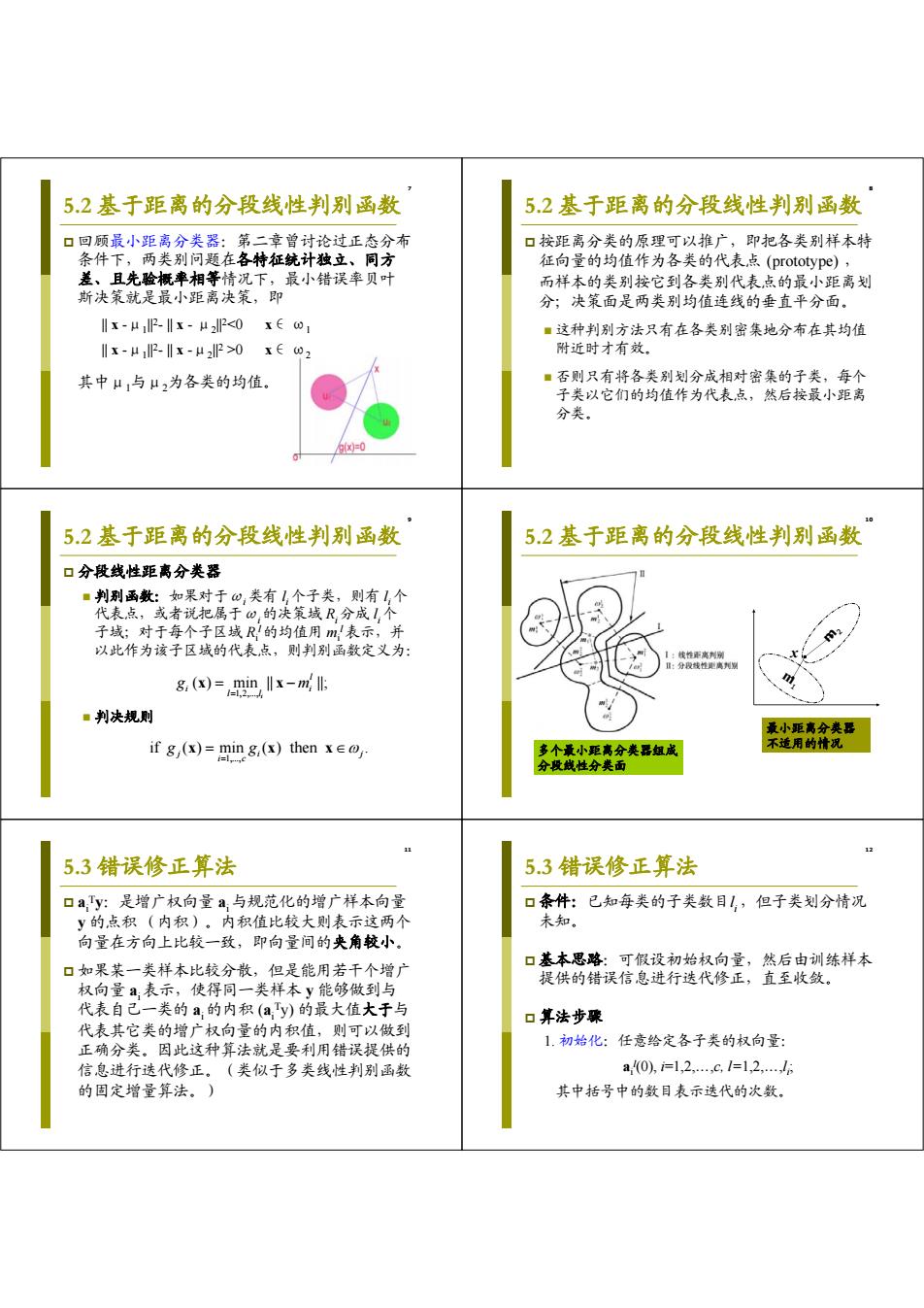
7 5.2 基于距离的分段线性判别函数 回顾最小距离分类器:第二章曾讨论过正态分布 条件下,两类别问题在各特征统计独立、同方 差、且先验概率相等情况下,最小错误率贝叶 斯决策就是最小距离决策,即 || x -μ1||2- || x - μ2||20 x∈ ω2 其中μ1与μ2为各类的均值。 8 5.2 基于距离的分段线性判别函数 按距离分类的原理可以推广,即把各类别样本特 征向量的均值作为各类的代表点 (prototype) , 而样本的类别按它到各类别代表点的最小距离划 分;决策面是两类别均值连线的垂直平分面。 这种判别方法只有在各类别密集地分布在其均值 附近时才有效。 否则只有将各类别划分成相对密集的子类,每个 子类以它们的均值作为代表点,然后按最小距离 分类。 9 5.2 基于距离的分段线性判别函数 分段线性距离分类器 判别函数:如果对于ωi 类有 l i 个子类,则有 l i 个 代表点,或者说把属于ωi 的决策域 Ri 分成 l i 个 子域;对于每个子区域 Ri l 的均值用 mi l 表示,并 以此作为该子区域的代表点,则判别函数定义为: 判决规则 1,2,..., ( ) min || ||; i l i i l l g m x x 1,..., if ( ) min ( ) then . j i j i c g g x xx 10 5.2 基于距离的分段线性判别函数 多个最小距离分类器组成 分段线性分类面 最小距离分类器 不适用的情况 m1 m2 x 11 5.3 错误修正算法 ai Ty:是增广权向量 ai与规范化的增广样本向量 y 的点积 (内积)。内积值比较大则表示这两个 向量在方向上比较一致,即向量间的夹角较小。 如果某一类样本比较分散,但是能用若干个增广 权向量 ai表示,使得同一类样本 y 能够做到与 代表自己一类的 ai的内积 (ai Ty) 的最大值大于与 代表其它类的增广权向量的内积值,则可以做到 正确分类。因此这种算法就是要利用错误提供的 信息进行迭代修正。(类似于多类线性判别函数 的固定增量算法。) 12 5.3 错误修正算法 条件:已知每类的子类数目l i ,但子类划分情况 未知。 基本思路:可假设初始权向量,然后由训练样本 提供的错误信息进行迭代修正,直至收敛。 算法步骤 1. 初始化:任意给定各子类的权向量: ai l (0), i=1,2,…,c, l=1,2,…,li ; 其中括号中的数目表示迭代的次数

5.3错误修正算法 5.3错误修正算法 口算法步骤 口算法步骤 2.检测与修正:对每次迭代所得增广权向量用训练 2.检测与修正 样本检测,如发生错误分类,则利用错分的信息 口如果存在某个或几个子类不满足上述条件,即存 进行修正: 在子类ω·的现有权向量,)使得 口先将某一j类的增广样本向量y:,与该类所有增广 权向量求内积a'因y,找到其中的最大值 a'y,≤ay,i≠J Wy,产,ry 则y,被错分类,需修正有关权向量。 口将y与其它非j类的权向量求内积,如 设y,=maxy aky,>ay,i=l1,2,,c,i≠方1=l,2, 则修正算法为a(k+)=a)+P, 则a《阳不影响y,的正确分类,不需修改。 a(k+1)=a"(k)-Py, 16 5.3错误修正算法 5.3错误修正算法 口算法步兼 口未知子类数目的情况(简介) 3.迭代与停止:利用新的权向量值对下一个训练样 ■树状分段线性分类器:先设计一个线性分类器, 本重复步骤二,直到算法收敛或者强迫其收敛。 将所有样本分成两个子类;若子类中有错分,则 在其中再分,直到全部样本正确分类。 口收敛性 ■在样本集确实能被分段线性判别函数正确划分的 情况下,迭代算法是收敛的。当该条件不满足 时,则需逐步减小p的数值,迫使其“收敛”,显 然会有相应的分类错误率存在
13 5.3 错误修正算法 算法步骤 2. 检测与修正:对每次迭代所得增广权向量用训练 样本检测,如发生错误分类,则利用错分的信息 进行修正; 先将某一 j 类的增广样本向量 yj ,与该类所有增广 权向量求内积 aj l(k) T yj ,找到其中的最大值 将 yj与其它非 j 类的权向量求内积,如 则 ai l (k) 不影响 yi的正确分类,不需修改。 ( ) max ( ) , 1,2, , j l T j l l j m T j k k j a y a y ( ) ( ) , 1,2, , , , 1, 2, , , mT lT j j i j i a ya y k k i ci j l l 14 5.3 错误修正算法 算法步骤 2. 检测与修正 如果存在某个或几个子类不满足上述条件,即存 在子类 ωi n 的现有权向量 ai n(k) 使得 则 yi被错分类,需修正有关权向量。 设 则修正算法为 ( ) ( ) , mT nT j ji j a ya y k ki j ' ' , ( ) max ( ) , n T nT j ij i i n a y ay k k ' ' ' ' ( 1) ( ) . ( 1) ( ) m m j j k j n n i ik j k k k k a ay a ay 15 5.3 错误修正算法 算法步骤 3. 迭代与停止:利用新的权向量值对下一个训练样 本重复步骤二,直到算法收敛或者强迫其收敛。 收敛性 在样本集确实能被分段线性判别函数正确划分的 情况下,迭代算法是收敛的。当该条件不满足 时,则需逐步减小ρk的数值,迫使其“收敛”,显 然会有相应的分类错误率存在。 16 5.3 错误修正算法 未知子类数目的情况(简介) 树状分段线性分类器:先设计一个线性分类器, 将所有样本分成两个子类;若子类中有错分,则 在其中再分…,直到全部样本正确分类