北京大学：《模式识别》课程教学资源（课件讲稿）特征的选择和提取（第一部分）

7.1引言 第七章 原始观测获取 特征的选择与提取 2009-11-24 信号 特征提取与选择 分类方法 分 特征提取 议计 预纯理 与远释 7.1引言 7.1引言 口特征的选择与提取是模式识别中重要而困难的一 口确定特征空间的不同层次 个环节： ■物理量的获取与转换白形成原始特征（测量) ■分析各种特征的有效性并选出最有代表性的特征 是模式识别的关键一步： 口实例： ■降低特征维数在很多情况下是有效设计分类器的 ·数字图像中的各像素灰度值： 重要课题； ·人体的各种生理指标 口三大类特征：物理、结构和数学特征 口原始特征分析： ■物理和结构特征：易于为人的直觉感知，但有时 ·原始测量不能反映对象本质； 难于定量描述，因而不易用于机器判别 ·高维原始特征不利于分类器设计：计算量大，冗 ■数学特征：易于用机器定量描述和判别，如基于 余，样本分布十分稀疏。 统计的特征 7.1引言 7.1引言 口确定特征空间的不同层次 口确定特征空间的不同层次 ■描述事物方法的选择与设计 ■特征空间的优化、降维 HSI 颜色空间 原始图像 距离 切割次数

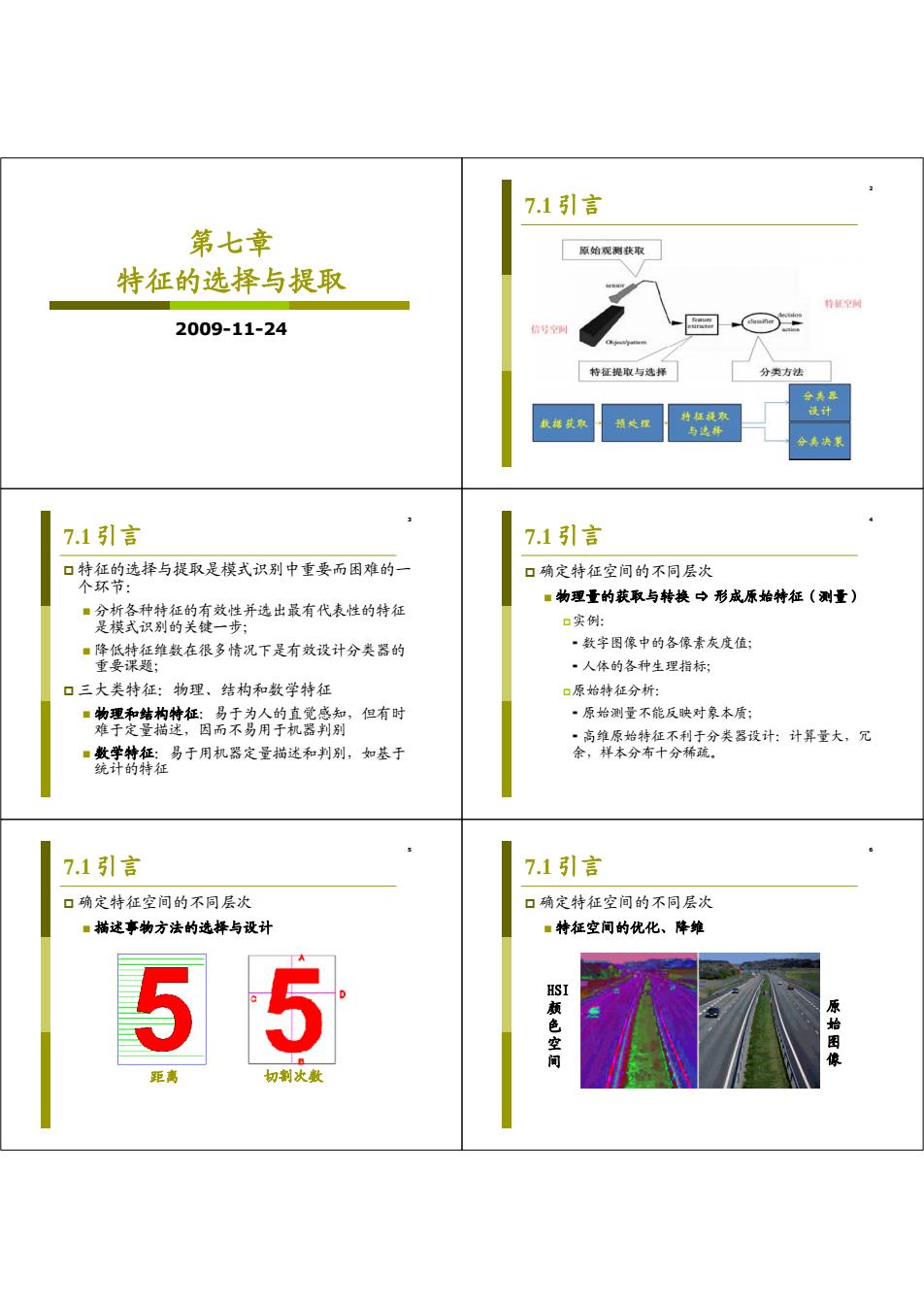
第七章 特征的选择与提取 2009-11-24 2 7.1 引言 3 7.1 引言  特征的选择与提取是模式识别中重要而困难的一 个环节：  分析各种特征的有效性并选出最有代表性的特征 是模式识别的关键一步；  降低特征维数在很多情况下是有效设计分类器的 重要课题；  三大类特征：物理、结构和数学特征  物理和结构特征：易于为人的直觉感知，但有时 难于定量描述，因而不易用于机器判别  数学特征：易于用机器定量描述和判别，如基于 统计的特征 4 7.1 引言  确定特征空间的不同层次  物理量的获取与转换  形成原始特征（测量） 实例：  数字图像中的各像素灰度值；  人体的各种生理指标； 原始特征分析：  原始测量不能反映对象本质；  高维原始特征不利于分类器设计：计算量大，冗 余，样本分布十分稀疏。 5 7.1 引言  确定特征空间的不同层次  描述事物方法的选择与设计 距离 切割次数 6 7.1 引言  确定特征空间的不同层次  特征空间的优化、降维 原 始 图 像 HSI 颜 色 空 间

7.1引言 7.1引言 口优化特征空间的两种基本方法 口优化特征空间的两种基本方法 ■特征选择(selection):从原始特征中挑选出最有 ■特征选择(selection):从原始特征中挑选出最有 代表性，分类性能最好的特征： 代表性，分类性能最好的特征： ■特征提取(extraction:用映射（或变换）的方法 ■特征提取(extraction):用映射（或变换）的方法 把原始特征变换为较少的新特征。 把原蛤特征变换为较少的新特征。 ■特征的选择与提取与具体问题有很大关系，目前 没有理论能给出对任何问题都有效的特征选择与 提取方法。 7.1引言 7.2类别可分离性判据 口特征选择与提取举例一细胞自动识别 口类别可分离性判据：衡量不同特征及其组合对分 ■原始测量：（正常与异常）细胞的数字图像： 类是否有效的定量准则： ■原始特征（特征的形成，找到一组代表细胞性质 口理想准则：某组特征使分类器错误概率最小； 的特征)：细胞面积，胞核面积，形状系数，光 密度，核内纹理，和浆比； 口常见类别可分离性判据： ■压缩特征：原始特征的维数仍很高，需压缩以便 于分类； ■基于距离的可分性判据： ▣特征选择：挑选最有分类信息的特征： ■基于概率分布的判据； ▣特征提取：数学变换； ■傅立叶变换或小波变换： ■熵函数的可分性判据。 ■用PCA方法作特征压编， 11 7.2类别可分离性判据 7.3.1基于距离的可分性判据 口实际的类别可分离性判据应满足的条件： 口实质：综合考虑不同类样本的类内聚合程度与类 间离散程度两个因素。 1. 度量特性：J,>0,ifi≠方J,=0,ifi=方J,=J 2. 与错误率有单调关系：J大一P小： 3. 当特征独立时有可加性：，化，。)产会 4. 单调性：J,(,x2,x)≤J(,x2,,x4X4月 Figure:Projection of the same set of samples onto two difterent lines in the directions marked as w.The figure on the right shows greater separation between the red and black projected points

7 7.1 引言  优化特征空间的两种基本方法  特征选择 (selection)：从原始特征中挑选出最有 代表性，分类性能最好的特征；  特征提取 (extraction)：用映射（或变换）的方法 把原始特征变换为较少的新特征。 8 7.1 引言  优化特征空间的两种基本方法  特征选择 (selection)：从原始特征中挑选出最有 代表性，分类性能最好的特征；  特征提取 (extraction)：用映射（或变换）的方法 把原始特征变换为较少的新特征。  特征的选择与提取与具体问题有很大关系，目前 没有理论能给出对任何问题都有效的特征选择与 提取方法。 9 7.1 引言  特征选择与提取举例 — 细胞自动识别  原始测量：（正常与异常）细胞的数字图像；  原始特征（特征的形成，找到一组代表细胞性质 的特征）：细胞面积，胞核面积，形状系数，光 密度，核内纹理，和浆比；  压缩特征：原始特征的维数仍很高，需压缩以便 于分类； 特征选择：挑选最有分类信息的特征； 特征提取：数学变换；  傅立叶变换或小波变换；  用PCA方法作特征压缩。 10 7.2 类别可分离性判据  类别可分离性判据：衡量不同特征及其组合对分 类是否有效的定量准则；  理想准则：某组特征使分类器错误概率最小；  常见类别可分离性判据：  基于距离的可分性判据；  基于概率分布的判据；  熵函数的可分性判据。 11  实际的类别可分离性判据应满足的条件： 1. 度量特性： 2. 与错误率有单调关系： 3. 当特征独立时有可加性： 4. 单调性： 0, if ; 0, if ; ; ij ij ij ji J    i jJ i jJ J 1 2 1 ( , ,..., ) ( ); d ij d ij k k J xx x J x    12 12 1 ( , ,..., ) ( , ,..., , ). ij d ij d d J xx x J xx x x   ij e J P 大 小;  7.2 类别可分离性判据 12 7.3.1 基于距离的可分性判据  实质：综合考虑不同类样本的类内聚合程度与类 间离散程度两个因素

7.3.1基于距离的可分性判据 7.3.1基于距离的可分性判据 口描述母体的离散程度 口有限样本集下离散度矩阵的估计 样本类均值向量： m=之 n知 样本总体均值向量： 母体类均值： H,=E,[x] "2a 母体总体均值 μ=ELx 5 样本类间离散度矩阵： 5.->P(m,-mXm,-my; 母体类间离散度矩阵： S,=2P,-,- 及-宫哈2心-画心-my 母体类内离散度矩阵： S.=2PE-4,x-4, 样本类内离散度矩阵： 一空供，心样木茨内协方差 7.3.1基于距离的可分性判据 7.3.1基于距离的可分性判据 口基于各类特征向量间平均距离的判据 口基于各类特征向量间平均距离的判据 J,=吃129,0房 ■代入欧式距离及m,m 类内平均 2台分人”，台台 平方距离 其中，x0∈0，k=l,…,n, xe0,1=l,…,n 度量两 类之间的（平 空fm-mrm 各类均值与 总体均值的 ,:先验概率 均)分离程度 平方距离 (红，：和x之间的距离度量： ■米用欧式距离：6(，x)=(k-x)'(K-x, m-m(m-m) JD为各类之间的平均平方距离。 即各类均值向量的平均平方距离。 17 7.3.1基于距离的可分性判据 7.3.1基于距离的可分性判据 口基于各类特征向量间平均距离的判据 口常用的基于类内类间距离的可分性判据 ■代入欧式距离及m,m J,()=tr(S.+S6方 -空2--】 J2(x)=tr(SS)方 (x)=In IS.I ls,T +空P[m-m旷m,- J,(x)=) tr(S,) ,w)=1S+S IS,I →J()=t(S+S) 基于距离的准则概念直观，计算方便：但与错误率没有 直接联系：当各类协差相差不大时，用此判据较好

13 7.3.1 基于距离的可分性判据  描述母体的离散程度 1 1 : [ ]; : [ ]; ( )( ) ; ( )( ) ; i i c T b ii i i c T w ii i i i E E P PE           μ x μ x S μ μμ μ S x μ x μ 母体类均值 母体总体均值 母体类间离散度矩阵： 母体类内离散度矩阵: 14 7.3.1 基于距离的可分性判据  有限样本集下离散度矩阵的估计 ( ) 1 1 1 () () 1 1 1 1 : ; : ; ( )( ) ; 1 ( )( ) ( : ). i i n i i k i k c i i i c T b ii i i c n i iT w i k ik i i k i c ii i i n P P P n P                     m x m m S m mm m S x mx m   样本类均值向量 样本总体均值向量 样本类间离散度矩阵： 样本类内离散度矩阵: 样本类内协方差阵 15 7.3.1 基于距离的可分性判据  基于各类特征向量间平均距离的判据  采用欧式距离： JD 为各类之间的平均平方距离。 () ( ) 1 1 11 ( ) ( ) 1 1 ( ) ( , ); 2 , 1, , , , 1, , , , : , ( , ) : ; j i n n c c i j d i j kl i j kl i j i ki i j lj j i j kl k l J PP n n k n l n P P             x xx    x x xx x x   其中， 先验概率 和 之间的距离度量 ( , ) ( ) ( ), T kl k l k l  xx x x x x   度量ωi，ωj两 类之间的（平 均）分离程度 16 7.3.1 基于距离的可分性判据  基于各类特征向量间平均距离的判据  代入欧式距离及 , : m mi () () 1 1 1 1 () ( )( ) ( )( ); i c n i Ti d i k ik i i k i c T ii i i J P n P                     x xmxm mmmm 类内平均 平方距离 各类均值与 总体均值的 平方距离 1 1 1 ( )( ) 2 c c T i j i j i j i j P P       mm mm ， 即各类均值向量的平均平方距离。 17 7.3.1 基于距离的可分性判据  基于各类特征向量间平均距离的判据  代入欧式距离及 , : m mi () () 1 1 1 1 () ( )( ) ( )( ); i c n i Ti d i k ik i i k i c T ii i i J P n P                     x xmxm mmmm ( ) tr( ). d wb J x SS     18 7.3.1 基于距离的可分性判据  常用的基于类内类间距离的可分性判据 1( ) ( ); w b J tr x SS   1 2 ( ) ( ); w b J tr  x SS  3 | | ( ) ln ; | | b w J  S x S 4 ( ) () ; ( ) b w tr J tr  S x S 5 | | () . | | w b w J   S S x S 基于距离的准则概念直观，计算方便；但与错误率没有 直接联系；当各类协差相差不大时，用此判据较好

7.3.1基于距离的可分性判据 7.3.1基于距离的可分性判据 口常见的距离度量 口常见的距离度量 ■s阶Minkowski度量 ■歌式距离 ,)=【-yk-s月 x、x,为d维向量，x4、x,为其第i个分量，i=l,…,d ■Chebychev距离 ■城市块(City block) o x,x）=maxa-xa 7.3.1基于距离的可分性判据 7.3.2直接应用举例 口常见的距离度量 口图像二值化：大津灰度图像阙值法(OtSu ■平方距离 thresholding) 8xk)=(x-x'Qx-x） ■实质是两类分类问题：确定一个灰度（特征值） 闵值将图像中的像素分类； Q是给定的正定标尺矩阵； ■算法基本思想：用类间离散度（方差）作为可分 ■非线性距离度量 性判据； H iff 6g(xxx)2T 6x,x)= 0 if 6(xs.x)<T H,T是非线性度量参数，δ（化x)是上述任何一种 度量， 24 7.3.2直接应用举例 7.3.2直接应用举例 Otsu thresholding Otsu thresholding ■设图像有L个灰度级，n,为灰度值为1的像素数 ■求解闲值： 目，图像总像素N=n+n2+…+nL; L T·=argmax o(T): ■夫度为的像素概率（估计）：B=是 ■演示： ■当前阙值T将图像分为两个部分，计算类间方差： J=062(T)=0(4-4)2+@,(4-4)尸， 其中：D=2ma(m=立p=1-a. =T+ 46(T)= ”4,4=h+04=2见

19 7.3.1 基于距离的可分性判据  常见的距离度量  s阶 Minkowski 度量  城市块（City block） 20 7.3.1 基于距离的可分性判据  常见的距离度量  欧式距离  Chebychev 距离 21 7.3.1 基于距离的可分性判据  常见的距离度量  平方距离 Q 是给定的正定标尺矩阵；  非线性距离度量 H,T 是非线性度量参数，δ(xk,xl ) 是上述任何一种 度量。 22 7.3.2 直接应用举例  图像二值化：大津灰度图像阈值法 (Otsu thresholding)  实质是两类分类问题：确定一个灰度（特征值） 阈值将图像中的像素分类；  算法基本思想：用类间离散度（方差）作为可分 性判据； 23 7.3.2 直接应用举例  Otsu thresholding  设图像有 L 个灰度级，ni 为灰度值为 i 的像素数 目，图像总像素  灰度为 i 的像素概率（估计）：  当前阈值 T 将图像分为两个部分，计算类间方差: ; i i n p N  1 2 ; Nnn n   L 1 1 0 1 2 22 0 0 11 01 0 1 1 0 1 0 0 11 1 ( ) ( ) ( ), ( ) ( ) 1 ( ), ( ) , ( ) , . T L i i i iT b TT T L i i i iT ip ip L T i i J T T pT p T T T ip                                    其中： ， 24 7.3.2 直接应用举例  Otsu thresholding  求解阈值：  演示： * 2 1 argm ax ( ); L b T T T   

7.3.3按距离度量的特征提取方法 7.3.3按距离度量的特征提取方法 口特征提取：把D个特征（原始特征x)通过变 口按欧式距离的特征提取准则函数 换变为d个新特征(y)，即y=A(x: J(A)=r(A'(S+S)A)月 ■目的：更好的分类和/或减少计算量； h=r[S.A'('sA小 ■线性变换： y=A'x; (A)=InA'S,A A'SA 目标：求A*,使得 口A是D×d维矩阵，通常D>d→特征压缩，特 征变换； (A)(A'S,A) J(y)=max J(A'x) (A] ir(A'SA) ■非线性情况下，可能希望D≤d,如广义线性分 类器SVM,NN. ATEA J5(A)= A'S.A ∑=S.+S6 7.3.3按距离度量的特征提取方法 7.3.3按距离度量的特征提取方法 口基于J,判据的特征提取一线性判别分析(LDA) 口基于J,判据的特征提取一LDA ■结论：2对线性非奇异变换具有不变性。 ■求J2的最大值 J(y)=tr(S-S;) .(A)=(A'S:A)(A'SA) (A'S.A)(ATS,A) =mA-'S:(A)"A'S,A =0→ BA =irA-STS,A -2SA(ASA)(ASA)(AS:A)+2SA(AS:A)=0 =ir[S.'S,A-A] =tr(SS,)=J2(x). (S:)"s:A=A(S)"s: 7.3.3按距离度量的特征提取方法 7.3.3按距离度量的特征提取方法 口基于J2判据的特征提取一LDA 口基于J,判据的特征提取一LDA ■求2的最大值 ■求2的最大值 口对称矩阵S,S%可被一个非奇异线性变换B (d×d维)同时对角化，且 →[S)S]A=A(BB）→[S'S]B=(aB)A B'SB=I,B'S,B=A; →[S)'s8p,=9,,i=l2,D 其中，I和A分别是将y空间进行线性变换后所 得特征空间Z的类内离散度矩阵和类间离散度矩 →，p,分别是(S)厂S的特征值和特征向量： 阵，即 z=B'y=BTA'x; →A的对角元素是(S)厂S的d个特征值： 且有J2(2)=J2(y) 矩阵(AB)由相应的d个特征向量组成：

25 7.3.3 按距离度量的特征提取方法  特征提取：把 D 个特征（原始特征 x）通过变 换变为 d 个新特征（y），即  目的：更好的分类和/或减少计算量；  线性变换：  A 是 D×d 维矩阵，通常 D>d  特征压缩，特 征变换；  非线性情况下，可能希望 D≤d，如广义线性分 类器 SVM，NN。 ; T y  A x y  A x ; 26 7.3.3 按距离度量的特征提取方法  按欧式距离的特征提取准则函数            1 1 2 3 4 5 () ; () ; ( ) ln ; () ; ( ) , . T w b T T w b T b T w T b T w T T w b w J tr J tr J tr J tr J               A AS SA A ASA ASA ASA A ASA ASA A ASA A A A SS ASA 目标：求A*, 使得   { } ( ) max . T J J  A y A x 27 7.3.3 按距离度量的特征提取方法  基于J2判据的特征提取 — 线性判别分析 (LDA)  结论：J2 对线性非奇异变换具有不变性。      *1* 2 1 1 1 1 1 1 1 1 1 2 () ( ) ( ) ( ). w b T T w b T T w b w b w b w b J tr tr tr tr tr tr J                                      y SS ASA ASA A S A ASA A S SA S SA A SS x 28 7.3.3 按距离度量的特征提取方法  基于 J2 判据的特征提取 — LDA  求 J2 的最大值              1 2 2 1 11 1 1 ( ) ( ) 0 2 20 ; Tx Tx w b x Tx Tx Tx x Tx ww b w bw xx yy wb wb J tr J                              A ASA ASA A A SA ASA ASA ASA SA ASA S SAAS S 29 7.3.3 按距离度量的特征提取方法  基于 J2 判据的特征提取 — LDA  求 J2 的最大值 对称矩阵 可被一个非奇异线性变换 B （d×d 维）同时对角化，且 其中，I 和 Λ 分别是将 y 空间进行线性变换后所 得特征空间 z 的类内离散度矩阵和类间离散度矩 阵，即 且有 , y y S S w b B S B  I, B S B  Λ; y b y T w T ; T TT z B  y BAx 2 2 J J ( ) ( ). z y  30 7.3.3 按距离度量的特征提取方法  基于 J2 判据的特征提取 — LDA  求 J2 的最大值               1 1 1 1 1 1 , 1,2, , , ( ) xx xx wb wb x x w b i ii x x ii w b x x w b i D d d                              S S A ABΛB S S AB AB Λ S S φ φ φ S S Λ S S AB  分别是 的特征值和特征向量; 的对角元素是 的 个特征值； 矩阵 由相应的 个特征向量组成；

7.3.3按距离度量的特征提取方法 7.3.3按距离度量的特征提取方法 口基于J,判据的特征提取一LDA 口基于J,判据的特征提取一LDA ■求J2的最大值 设矩阵SS。的特征值为，，…，0， 令C=AB, 且12232…2如， →S)'SC=Cw→Cs8c=CsCw 则取前d个特征值对应的特征向量p1,p2,,pa, →J,y)=r[CsC'(csc]=r()=∑ 组成的线性变换矩阵A=[p,p2,…,p]) 则A能使降维后的特征空间的J,y)判据值最大 →当，，是(S)S的D个特征值中最大的d个， 口J3,J对线性非奇异变换具有不变性，J1J4与坐 J(y)达到最大值。 标系相关，但求解极值的结论相同。 7.3.3按距离度量的特征提取方法 7.3.3按距离度量的特征提取方法 口特征提取流程图 口LDA的局限性 收集样本 根据判据条件 计算特征矩阵 计算特征值 求特征向量 I 确定变换矩阵 25 7.3.3按距离度量的特征提取方法 7.3.3按距离度量的特征提取方法 口例：给定先验概率相等的两类，其均值向量分别 口解： 为： 4=1,3,-1]P,μ=l,-1,1]T,协方差矩阵 混合均值：μ=μ，+)=01,0： 是： 「410 「2101 =140， =120月 类离微度矩降：、玄以-p以-p-从- 001 001 「3101 类内离散度矩阵：S。= 8+2)130月 求用J2判据的最优特征提取 001 口思路：应先求S1S,再求此矩阵的特征矩阵。 「3-10] S-l= -1305 008

31 7.3.3 按距离度量的特征提取方法  基于 J2 判据的特征提取 — LDA  求 J2 的最大值          1 1 * 2 1 1 * * 1 2 () ; , ( ) x x Tx Tx wb b w d Tx Tx wb i i x x d wb J tr tr D d J                             C = AB S SCCΛ CSC CSCΛ y CSC CSC Λ S S y  令 ， ， 是 的 个特征值中最大的 个， 达到最大值。 当 32 7.3.3 按距离度量的特征提取方法  基于 J2 判据的特征提取 — LDA  J3, J5 对线性非奇异变换具有不变性，J1, J4 与坐 标系相关，但求解极值的结论相同。 设矩阵 的特征值为 且 则取前 d 个特征值对应的特征向量 组成的线性变换矩阵 则 A 能使降维后的特征空间的 J2(y) 判据值最大 1 w b  S S , , , , 1 2   D 1 2 ,      D 1 2 ,,, , φφ φ  d A  φφ φ 1 2 ,,, ,  d  33 7.3.3 按距离度量的特征提取方法 收集样本 根据判据条件 计算特征矩阵 计算特征值 确定变换矩阵 求特征向量  特征提取流程图 34 7.3.3 按距离度量的特征提取方法  LDA 的局限性 35 7.3.3 按距离度量的特征提取方法  例：给定先验概率相等的两类，其均值向量分别 为：μ1=[1,3,-1]T，μ2=[-1,-1,-1]T，协方差矩阵 是： 求用 J2 判据的最优特征提取。  思路：应先求 Sw -1 Sb，再求此矩阵的特征矩阵。 1 2 410 210 1 4 0, 1 2 0 001 001      Σ Σ ； 36 7.3.3 按距离度量的特征提取方法  解： 1 2   2 1 21 2 1 1 2 1 1 ( ) 0,1,0 2 1 1 ( )( ) ( )( ) 2 4 310 1 ( ) 130 2 001 3 10 1 1 3 0 ; 8 0 08 T T T b ii i w w                                   μ μμ S μ μμ μ μ μ μ μ S Σ Σ S 混合均值： ； 类间离散度矩阵： ； 类内离散度矩阵： ；

7.3.3按距离度量的特征提取方法 口注意：Sw1S的秩是l,故Sw1Sb只有一个非零 特征值；即所求线性变换矩阵A是D×1矩阵， 是一个向量，求解a需解方程 SSa=4a →S4-%X4-4a=和 ~4-4a是标量 a=s4-4)=专5-8

37 7.3.3 按距离度量的特征提取方法  注意：Sw -1 Sb 的秩是1，故 Sw -1 Sb只有一个非零 特征值；即所求线性变换矩阵 A 是D×1 矩阵， 是一个向量，求解 a 需解方程   1 1 1 1 21 2 1 1 2 1 1 2 1 ( )( ) 4 1 () 4 1 ( ) 1,5, 8 . 8 w b T w T T w                     S Sa a S aa a a S  是标量