北京大学：《模式识别》课程教学资源（课件讲稿）非监督学习方法

8.0引言 口有监督学习(supervised learning:用已知类别的 第八章非监督学习方法 样本训练分类器，以求对训练集数据达到某种最 优，并能推广到对新数据的分类。 2009-12-8 口非监督学习(unsupervised learning}:样本数据类 别未知，需要根据样本间的相似性对样本集进行 分类（聚类，clustering). ■在一堆数据中寻找一种“自然分组”(C组)。要 求同组（类别）的样本较为相似，而不同组的样 本间有明显不同。 8.0引言 8.0引言 口监督与非监督学习方法比较 口监督与非监督学习方法比较 ■监督学习方法必须要有训练集与测试样本。在训 练集中找规律，而对测试样本使用这种规律：而 非监督学习只有一组数据，在该组数据集内寻找 规律。 ■监督学习方法的目的是识别事物，给待识别数据 加上标号，因此训练样本集必须由带标号的样本 组成。而非监督学习方法只有要分析的数据集本 身，没有标号。如果发现数据集呈现某种聚集 性，则可按自然的聚集性分类，但不以与某种预 先的分类标号对上号为目的。 8.0引言 8.0引言 口主要的非监督学习方法 口聚类是一个难以被严格定义的问题，因为“自然 分组”本身就很抽象，且可能因人而异。 ■基于概率密度函数估计的直接方法：设法找到各 类别在特征空间的分布参数再进行分类。比如直 方图方法。 口需要解决两个问题： ■如何度量样本之间的相似性？ 。基于样本间相似性度量的间接聚类方法：设法定 出不同类别的核心或初始类核，然后依据样本与 ■如何衡量某一种分组的好坏？（即目标函数） 各核心之间的相似性度量将样本聚集成不同类别。 口寻找“最优分组”的计算复杂度太高，故一般的聚 类算法都是近似算法

第八章 非监督学习方法 2009-12-8 2 8.0 引言  有监督学习 (supervised learning)：用已知类别的 样本训练分类器，以求对训练集数据达到某种最 优，并能推广到对新数据的分类。  非监督学习 (unsupervised learning)：样本数据类 别未知，需要根据样本间的相似性对样本集进行 分类 (聚类，clustering)。  在一堆数据中寻找一种“自然分组”（C 组）。要 求同组（类别）的样本较为相似，而不同组的样 本间有明显不同。 3 8.0 引言  监督与非监督学习方法比较 4 8.0 引言  监督与非监督学习方法比较  监督学习方法必须要有训练集与测试样本。在训 练集中找规律，而对测试样本使用这种规律；而 非监督学习只有一组数据，在该组数据集内寻找 规律。  监督学习方法的目的是识别事物，给待识别数据 加上标号，因此训练样本集必须由带标号的样本 组成。而非监督学习方法只有要分析的数据集本 身，没有标号。如果发现数据集呈现某种聚集 性，则可按自然的聚集性分类，但不以与某种预 先的分类标号对上号为目的。 5 8.0 引言  主要的非监督学习方法  基于概率密度函数估计的直接方法：设法找到各 类别在特征空间的分布参数再进行分类。比如直 方图方法。  基于样本间相似性度量的间接聚类方法：设法定 出不同类别的核心或初始类核，然后依据样本与 各核心之间的相似性度量将样本聚集成不同类别。 6 8.0 引言  聚类是一个难以被严格定义的问题，因为“自然 分组”本身就很抽象，且可能因人而异。  需要解决两个问题：  如何度量样本之间的相似性？  如何衡量某一种分组的好坏？（即目标函数）  寻找“最优分组”的计算复杂度太高，故一般的聚 类算法都是近似算法

8.1单峰子集的分离方法 8.1.1投影方法 口基本思想：把特征空间分为若干个区域，在每个 口一维空间中的单峰分离 区域上混合概率密度函数是单峰的，每个单峰区 ■对样本集K-{x}应用直方图方法估计概率密度 域对应一个类别。 函数，找到概率密度函数的峰以及峰之间的谷 口例：如下图所示， 底，以谷底为闲值对数据进行分割。 x=0和=0这两个 超平面可以把(xy) 平面分成四个单峰 区域。 8.1.1投影方法 8.1.1投影方法 口多维空间y中直接划分成单峰区域比较困难， 口确定合适的坐标系统山 把它投影到一维空间x中简化问题（降维）。 ■启发式的方法一使投影{uy}的方差最大：方 口基本原理：考查样本某一分量的统计值，其分布 差越大，类之间分离的程度也可能越大； 往往呈现多峰形式；找到低谷，将峰值分别划分 ■满足这样要求的Ⅲ是样本协方差矩阵的最大特征 于不同的区域，每个 值对应的特征向量。 区域只有一个高峰， 从而把聚在同一高峰 下的样本划分为一类。 1 12 8.1.1投影方法 8.1.1投影方法 口确定合适的坐标系统ū 口算法步骤 ■存在问题：这样选择的Ⅱ有时并不能产生多峰的 1.计算样本y的混合协方差矩阵的最大特征值对 边缘密度函数」 应的特征向量u,把样本数据投影到u上(y: 2.对投影后的数据，用直方图法求边缘概率密度 函数： 3. 找到边缘概率密度函数的各谷，点，在这些谷，点 上作垂直于ū的超平面把数据划分成几个子集； 4.如没有谷点，则用下一个最大的特征值代替； 5.对所得到的各个子集进行同样的过程，直至每 个子集都是单峰为止

7 8.1 单峰子集的分离方法  基本思想：把特征空间分为若干个区域，在每个 区域上混合概率密度函数是单峰的，每个单峰区 域对应一个类别。  例：如下图所示， x=0 和 y=0 这两个 超平面可以把 (x,y) 平面分成四个单峰 区域。 8 8.1.1 投影方法  一维空间中的单峰分离  对样本集 KN={xi } 应用直方图方法估计概率密度 函数，找到概率密度函数的峰以及峰之间的谷 底，以谷底为阈值对数据进行分割。 9 8.1.1 投影方法  多维空间 y 中直接划分成单峰区域比较困难， 把它投影到一维空间 x 中简化问题（降维）。  基本原理：考查样本某一分量的统计值，其分布 往往呈现多峰形式；找到低谷，将峰值分别划分 于不同的区域，每个 区域只有一个高峰， 从而把聚在同一高峰 下的样本划分为一类。 10 8.1.1 投影方法  确定合适的坐标系统 u  启发式的方法 — 使投影 {uTy} 的方差最大：方 差越大，类之间分离的程度也可能越大；  满足这样要求的 u 是样本协方差矩阵的最大特征 值对应的特征向量。 11 8.1.1 投影方法  确定合适的坐标系统 u  存在问题：这样选择的 u 有时并不能产生多峰的 边缘密度函数。 12 8.1.1 投影方法  算法步骤 1. 计算样本 y 的混合协方差矩阵的最大特征值对 应的特征向量u，把样本数据投影到u上 (uTy)； 2. 对投影后的数据，用直方图法求边缘概率密度 函数; 3. 找到边缘概率密度函数的各谷点，在这些谷点 上作垂直于u的超平面把数据划分成几个子集； 4. 如没有谷点，则用下一个最大的特征值代替； 5. 对所得到的各个子集进行同样的过程，直至每 个子集都是单峰为止

8.1.2单峰子集分离的迭代算法 8.1.2单峰子集分离的迭代算法 口假设数据集S有一个划分 口考虑两个子集（类）的类条件概率密度函数加权 s-Ur. 估计值之间的“距离” i=1 其中T:互不相交，且=N,∑N=N=S f(I)-f(yrp(y)dy. 口估计各类的加权类条件概率密度函数： f(I)-pIT f(r) 可用Parzen方法估计类条件概率密度 1 P(yIr,)= K(y.y).y.erc 根据使两类的类条件概幸密度函数加权 估计值之间的“距离“最大进行类别划分 8.1.2单峰子集分离的迭代算法 8.1.2单峰子集分离的迭代算法 口聚类准则：求子集划分能最大化 口求解 J=含2Ir,)-f1r,rpd ■考虑J的变化量 第一项恒 大于0 AJ=[2cN,]p(y)dy 口求解 ■考查某个样本y从T;移入，得到新的广，广 +2cJ[f(yIr)-f(yIr,)fp(y)dy, f(ylf,)zf(ylr,), 一般N较大： f(ylf,)sf(ylr,), 只有当y很接近 时，△才能 第二项取决于「「)：差越大，A越大。 或=-=k 注意：当y不是y的近邻时，△的值接近于0。 且 不接近于0。 8.1.2单峰子集分离的迭代算法 8.1.2单峰子集分离的迭代算法 口求解 口算法步骤 ■通过把y从下，移入下，使得J增大，故移入时 1.对数据集S选定一个初始划分； 应该选择使△J尽可能大的「：，即选择 2.对S中的每一个样本y,逐一计算fyI口)， f(y:r,)=maxf(y), 并把y重新分配到使得fy:ID),最大的子集 从而使得△J最大： 中； ■如存在两个（或以上）子集的fy.C,)最大（相 3.如果有任何点进行了类别的转移，则重复上一 等)，则可移入其中任意一类。 步骤；直到不再有样本发生转移

13 8.1.2 单峰子集分离的迭代算法  假设数据集 S 有一个划分 其中Γi 互不相交，且  估计各类的加权类条件概率密度函数： 可用 Parzen 方法估计类条件概率密度 , 1 i c i S     N , N N S ; i i  i  i   ( | ) ( | ); i i i N f p N y y   1 1 ( | ) ( , ), . N i i i ii j i p K N  y yy y     14 8.1.2 单峰子集分离的迭代算法  考虑两个子集（类）的类条件概率密度函数加权 估计值之间的“距离”   ( | ) ( | ) ( ) , 2  f y i  f y j p y dy 根据使两类的类条件概率密度函数加权 估计值之间的“距离”最大进行类别划分 15 8.1.2 单峰子集分离的迭代算法  聚类准则：求子集划分能最大化  求解  考查某个样本 yk 从Γj 移入Γi,得到新的 2 1 1 1 [ ( | ) ( | )] ( ) ; 2 c c i j i j J ff p d         y y yy i j ~ , ~ ( | ) ( | ), ( | ) ( | ), 1 ( ) , ; i i i j j j k ffK f f N f f          y y y y y y   且 一般 N 较大； 只有当y很接近 yk时，△fi 才能 不接近于0。 16 8.1.2 单峰子集分离的迭代算法  求解  考虑 J 的变化量   2 2 () 2 ( | ) ( | ) () , i i ji J cf p d c f f fp d             y y y y yy 第一项恒 大于0 第二项取决于 f(y|Γi )-f(y|Γj )：差越大，△J 越大。 注意：当 y 不是 yk的近邻时，△fi 的值接近于0。 17 8.1.2 单峰子集分离的迭代算法  求解  通过把 yk从Γj 移入Γi，使得 J 增大，故移入时 应该选择使△J 尽可能大的Γi，即选择 从而使得△J 最大；  如存在两个（或以上）子集的 最大（相 等），则可移入其中任意一类。 ( | ) max ( | ), k l l k i f y   f y  ( | ) k i f y  18 8.1.2 单峰子集分离的迭代算法  算法步骤 1. 对数据集 S 选定一个初始划分； 2. 对 S 中的每一个样本 y，逐一计算 并把 y 重新分配到使得 最大的子集 中； 3. 如果有任何点进行了类别的转移，则重复上一 步骤；直到不再有样本发生转移。 ( | ), k i f y  ( | ), k i f y 

8.2类别分离的间接方法 8.2.1C-均值算法（K-均值/means) 口三个要点： 口问题假设：对样本集K={x}尚不知每个样本的 ■样本与样本/样本聚类间相似性的度量； 类别，但可假设所有样本可分为c类，各类样本 ■准则函数：聚类质量的判别标准； 在特征空间依类聚集，且近似球形分布； ■初始分类方法及迭代算法； 口基本思路：用一代表点(prototype)来表示一个 可盖化案英中图 聚类，如类内均值m,来代表聚类K; 初始聚为 口目标： 口聚类准则：误差平方和J ■类内元素相似性高： 家类合回y→聚类结束 ■类间元素相似性低。 J=会名mf 修改聚为 8.2.1C-均值算法(K-均值/means) 8.2.1C-均值算法（K-均值/means 口求解 口C-均值算法步骤 ■假设已有一个初始划分，考查「k中的样本y,如 1.选择一个初始划分，并计算各类均值； 把y移入「，J的改变量是 2.选择一个样本y,设y∈；如N,=l,则重选 w=或-m+- y;否则继续； 3. 分别计算如把y移动到其他各类中造成△； 如果△J<0, 4.如果所有的△都大于0，则不移动y。否则移 动y到产生最小△的类； →把y从「。移入「，会减小J。 更新相关类的均值，以及J值： 如连续迭代N次J值不变，则停止；否则转2。 8.2.1C-均值算法(K-均值/means) 8.2.1C-均值算法（K-均值/means) 初始代表，点的选择 初始分类方法 1.经验选择； 1,最近距离法：离哪个代表点近就归入哪一类； 2.随机分成c类，选各类重心作为代表点； 2. 最近距离法归类，但每次都重新计算类代表 3.“密度法”选择代表点： 点； 口计算每个样本的一定球形邻域内的样本数作为” 密度”，选“密度”最大的样本点作为第一个代表 3. 直接划分初始分类：第一个样本自成一类，第 点，在离它一定距离之外最大“密度”点作为第二 二个样本若离它小于某距离阈值则归入此类， 个代表点，，依此类推： 否则建新类，… 4.用前c个样本点作为代表点； 4.将特征归一化，用样本各特征之和作为初始分 5.用c-1聚类求c个代表点：各类中心外加离它 类依据。 们最远的样本点，从1类开始

19 8.2 类别分离的间接方法  三个要点：  样本与样本/样本聚类间相似性的度量；  准则函数：聚类质量的判别标准；  初始分类方法及迭代算法；  目标：  类内元素相似性高；  类间元素相似性低。 20 8.2.1 C-均值算法（K-均值/means）  问题假设：对样本集 KN={xi } 尚不知每个样本的 类别，但可假设所有样本可分为 c 类，各类样本 在特征空间依类聚集，且近似球形分布；  基本思路：用一代表点 (prototype) 来表示一个 聚类，如类内均值 mi 来代表聚类 Ki ；  聚类准则：误差平方和 J 2 1 . i c i i J      y y m 21  求解  假设已有一个初始划分，考查Γk中的样本 y，如 把 y 移入Γj，J 的改变量是 8.2.1 C-均值算法（K-均值/means） 2 2 , 1 1 0 k j k j k j k j N N J N N J J             ym ym y 如果 ， 把 从 移入 会减小 。 22  C-均值算法步骤 1. 选择一个初始划分，并计算各类均值； 2. 选择一个样本 y，设 如 则重选 y；否则继续； 3. 分别计算如把 y 移动到其他各类中造成 4. 如果所有的 都大于0，则不移动 y。否则移 动 y 到产生最小 的类； 5. 更新相关类的均值，以及 J 值； 6. 如连续迭代 N 次 J 值不变，则停止；否则转2。 8.2.1 C-均值算法（K-均值/means） ; i y 1, Ni J; J J 23  初始代表点的选择 1. 经验选择； 2. 随机分成 c 类，选各类重心作为代表点； 3. “密度法”选择代表点：  计算每个样本的一定球形邻域内的样本数作为” 密度”，选“密度”最大的样本点作为第一个代表 点，在离它一定距离之外最大“密度”点作为第二 个代表点，…，依此类推； 4. 用前 c 个样本点作为代表点； 5. 用 c-1 聚类求 c 个代表点：各类中心外加离它 们最远的样本点，从 1 类开始。 8.2.1 C-均值算法（K-均值/means） 24  初始分类方法 1. 最近距离法：离哪个代表点近就归入哪一类； 2. 最近距离法归类，但每次都重新计算类代表 点； 3. 直接划分初始分类：第一个样本自成一类，第 二个样本若离它小于某距离阈值则归入此类， 否则建新类，…… 4. 将特征归一化，用样本各特征之和作为初始分 类依据。 8.2.1 C-均值算法（K-均值/means）

8.2.1C-均值算法(K-均值/means) 8.2.1C-均值算法（K-均值/means Minimize the sum of within- 口讨论 cluster square errors ■优，点 09 Start with c cluster centers 口时间复杂度OW: Iterate between 口简单易实现； 1.Assign data points to the 口适用于“球形”分布的数据： closest cluster centers 05 ■用于非监督模式识别的问题 2.Adjust the cluster centers to be the means of the data 44 口要求类别数已知； points 02 口是最小方差划分，并不一定能反映内在分布： 口与初始划分有关，不保证全局最优。 User specified parameters:c, 602040608 initialization of cluster centers ■存在不少变种：初始划分的方法；更新均值的时 k-Means,k=3 机；聚类数目的动态决定，等等。 8.2.2样本和核相似性度量的聚类算法 8.2.2样本和核相似性度量的聚类算法 口采用一个“核”K代表一个类「射 口算法步骤，类似于C均值： 口核K可以是一个函数，一个点集，某种适当的 1.选择初始划分，并计算初始核K,户1，，c 分类模型等等。 2.按照如下规则把各样本分类： 口定义样本和各类的核之间的相似性度量△(y,K方 if△(y,K)=min△(y,K,),then y∈r 口聚类准则函数，即最小化的目标函数 3.更新核，并重复步骤2-3直至收敛 J=∑∑Ay,K,) ■C-均值算法=核是类均值，样本和核之间的相 j=l yer, 似性度量是欧式距离的特例。 8.2.2样本和核相似性度量的聚类算法 8.2.2样本和核相似性度量的聚类算法 口算法收敛的充分条件：准则函数J满足 口正态核函数：适用于各类为正态分布 如果JT,K)≤J(T,K), K,,)= r4空个0-m,r实g-m小 那么J(广，K)≤J(T,K)方 ■参数集V=(m,三，)从各类样本中估计： ·「，K:修正之前的分类集合和对应的核集合； ■相似性度量： ■广，衣：修正之后的分类集合和对应的核集合： aG.K)=0-m,y0-m,)+号e1色

25 8.2.1 C-均值算法（K-均值/means） 26  讨论  优点 时间复杂度 O(N)； 简单易实现； 适用于“球形”分布的数据；  用于非监督模式识别的问题 要求类别数已知； 是最小方差划分，并不一定能反映内在分布； 与初始划分有关，不保证全局最优。  存在不少变种：初始划分的方法；更新均值的时 机；聚类数目的动态决定，等等。 8.2.1 C-均值算法（K-均值/means） 27 8.2.2 样本和核相似性度量的聚类算法  采用一个“核” Kj 代表一个类Γj ；  核 Kj 可以是一个函数，一个点集，某种适当的 分类模型等等。  定义样本和各类的核之间的相似性度量  聚类准则函数，即最小化的目标函数 ( , ); K j  y ( , ). 1      c j y j j J y K 28  算法步骤，类似于 C-均值： 1. 选择初始划分，并计算初始核 Kj ，j=1,…,c； 2. 按照如下规则把各样本分类： 3. 更新核，并重复步骤 2-3 直至收敛。  C-均值算法 = 核是类均值，样本和核之间的相 似性度量是欧式距离的特例。 8.2.2 样本和核相似性度量的聚类算法 f Δ( ) minΔ( ), then ; 1 i j i , ,c j i ,K  ,K   y y y  29  算法收敛的充分条件：准则函数 J 满足  ： 修正之前的分类集合和对应的核集合；  ： 修正之后的分类集合和对应的核集合； 8.2.2 样本和核相似性度量的聚类算法 ( , ) ( , ), ( , ) ( , ); J J J J   Γ K Γ K Γ K Γ K    如果 那么 Γ,K Γ  ,K 30  正态核函数：适用于各类为正态分布  参数集 从各类样本中估计；  相似性度量： 8.2.2 样本和核相似性度量的聚类算法 1 /2 1/2 1 1 ˆ ( , ) exp ( ) ( ) (2 ) | | ˆ 2 T j j jj j d j K V            y ym Σ y m Σ ， ) ˆ ( , Vj  m j Σj 1 1 1 ˆ ˆ ( , ) ( ) ( ) log| | . 2 2 T Kj jj j j      y ym Σ y m Σ

8.2.2样本和核相似性度量的聚类算法 8.2.3近邻函数准则函数 口主轴核函数：适用于各类样本集中分布在各自 口近邻函数：不同样本间相似性的度量 的主轴方向上的子空间里的情况 K(y,V,)=UTy, ■如果y是y的第I个近邻，则y对y的近邻系数 为上 其中U,=u,u2,,",是第j类样本协方差阵的 ■如果y是y,的第K个近邻，则y对y的近邻系数 前山，个最大特征值对应的特征向量系统： 为K △y,k,)=【y-m,)-U,Ugg-m, ■和y之间的近邻函数： ((y-m,)-U,UJ(y-m, 一g与 am=1+K-2,i≠j方 是样本到主轴子空间的距离。 8.2.3近邻函数准则函数 8.2.3近邻函数准则函数 口连接： 如y,和y,被分到同一类，则称它们相互 口连接损失可使得密度相近的点容易聚成一类 连接； 口每个连接对应一个连接损失：两点之间的近邻函 损失 数c可时 口一个点和其自身的连接损失为C=2W(N是样本 总数)，以惩罚只有一个点的聚类； 口不同类的点不存在连接，故连接损失Q=0 口总类内损失： 损失：ak=1+6-2=5,a=2+1-2=上 8.2.3近邻函数准则函数 8.2.3近邻函数准则函数 口第i类和第j类之间的最小近邻函数值定义为： 口总类间损失： y,（a) 口记第i类内最大连接损失为cmar; 口总类内损失： 口定义第i类和第j类之间的连接损失为B),其 设计目标是：如果两类间的最小近邻值小于任何 4-224, 一方的类内的最大连接损失时，损失代价就是正 的，从而应该考虑把这两类合并。 口准则函数： -[7n-4m.)+(7g-0mn小f70>0m70>0m Y。十an码 f705a7g之0 J=Lwihin +Lbenreen 7。+aen 70>07,≤0= 7w中01mt+0a f7w≤4m7≤01

31  主轴核函数：适用于各类样本集中分布在各自 的主轴方向上的子空间里的情况 8.2.2 样本和核相似性度量的聚类算法   前 个最大特征值对应的特征向量系统； 其中 是第 类样本协方差阵的 , , , ( , ) , 1 2 j j d T j j d j K V j U u u u y U y        ( ) ( ) ( , ) ( ) ( ) 是样本到主轴子空间的距离。 j T j j j T j T K j j j j y m U U y m y y m U U y m          32 8.2.3 近邻函数准则函数  近邻函数：不同样本间相似性的度量  如果 yi 是 yj 的第 I 个近邻，则 yi 对 yj 的近邻系数 为 I;  如果 yj 是 yi 的第 K 个近邻，则 yj 对yi 的近邻系数 为 K;  yi 和 yj 之间的近邻函数： I K 2, i j; ij     33 8.2.3 近邻函数准则函数  连接：如 yi和 yj被分到同一类，则称它们相互 连接；  每个连接对应一个连接损失：两点之间的近邻函 数αij ;  一个点和其自身的连接损失为αii=2N（N 是样本 总数），以惩罚只有一个点的聚类；  不同类的点不存在连接，故连接损失αij=0;  总类内损失： 1 1 . N N within ij i j L      34 8.2.3 近邻函数准则函数  连接损失可使得密度相近的点容易聚成一类 1 6  2  5,  2 1 2 1; 损失：ik ij 35 8.2.3 近邻函数准则函数  第 i 类和第 j 类之间的最小近邻函数值定义为：  记第 i 类内最大连接损失为αimax ;  定义第 i 类和第 j 类之间的连接损失为βij ，其 设计目标是：如果两类间的最小近邻值小于任何 一方的类内的最大连接损失时，损失代价就是正 的，从而应该考虑把这两类合并。   , min , k il j ij ij      y y 36 8.2.3 近邻函数准则函数  总类间损失：  总类内损失：  准则函数： ; between ij i j L     1 1 ; N N within ij i j L      . Lwithin Lbetween J  

8.2.3近邻函数准则函数 8.3分级聚类方法 口算法步骤 口要解决的问题：按相似性、或内在联系、或本 1.计算距离矩阵△g=△(yy方 质把各种事物组成有层次的结构，把最接近的划 2. 用距离矩阵计算近邻矩阵M,My表示y,是y 归一类，然后把相近的几个类再合并成一个类； 的第几个近邻： 口目的与用途：将复杂的事物组织与管理起来； 3. 计算近邻函数矩阵Lg=M,+Mn-2L,Lm=2N 口技术问题：如何定义相似性？ 4在L中，每个点与其最近邻连接，形成初始的 ■可按度量值之间的差异。 划分： 5. 生水题教小 动态聚类算法 分级聚类算法 (建立连接)。重复至没有新的连接为止。 进代 非选代 8.3分级聚类方法 8.3分级聚类方法 口自底向上逐步合并：从各类只有一个样本点开 口自顶向下逐步分割 始，逐级考查类间相似度并合并，每级只合并两 类，直到最后所有样本都归到一类。 yi.y2.y3 y ys y2yy1 yo ys y3 9 2水平 90 水平1 y1,y2,y3 4水甲 0的 相似性尺度 水平2 y ys 6水 水平3y 40 42 8.3分级聚类方法 8.3分级聚类方法 口两个聚类K与K之间的相似性度量 口算法步骤：N个样本自底向上逐步合并一类 ■最近距离(single-link): 1.初始化：每个样本自成一类（划分水平1）； △(K,K)=m9ò(，y), yeK 2. K水平划分：计算已有的c=W-K+2个类的类间距 。最远距离(complete-link): 离矩阵Dl=[d依，其最小元素记作dK, 相应的两个类合并成一类： A(KK)=max 8(x.y). yek, 3.重复第2步，直到形成包含所有样本的类（划分 ■均值距离(average-link): 水平N). △(K,K,)=6(m,m,)

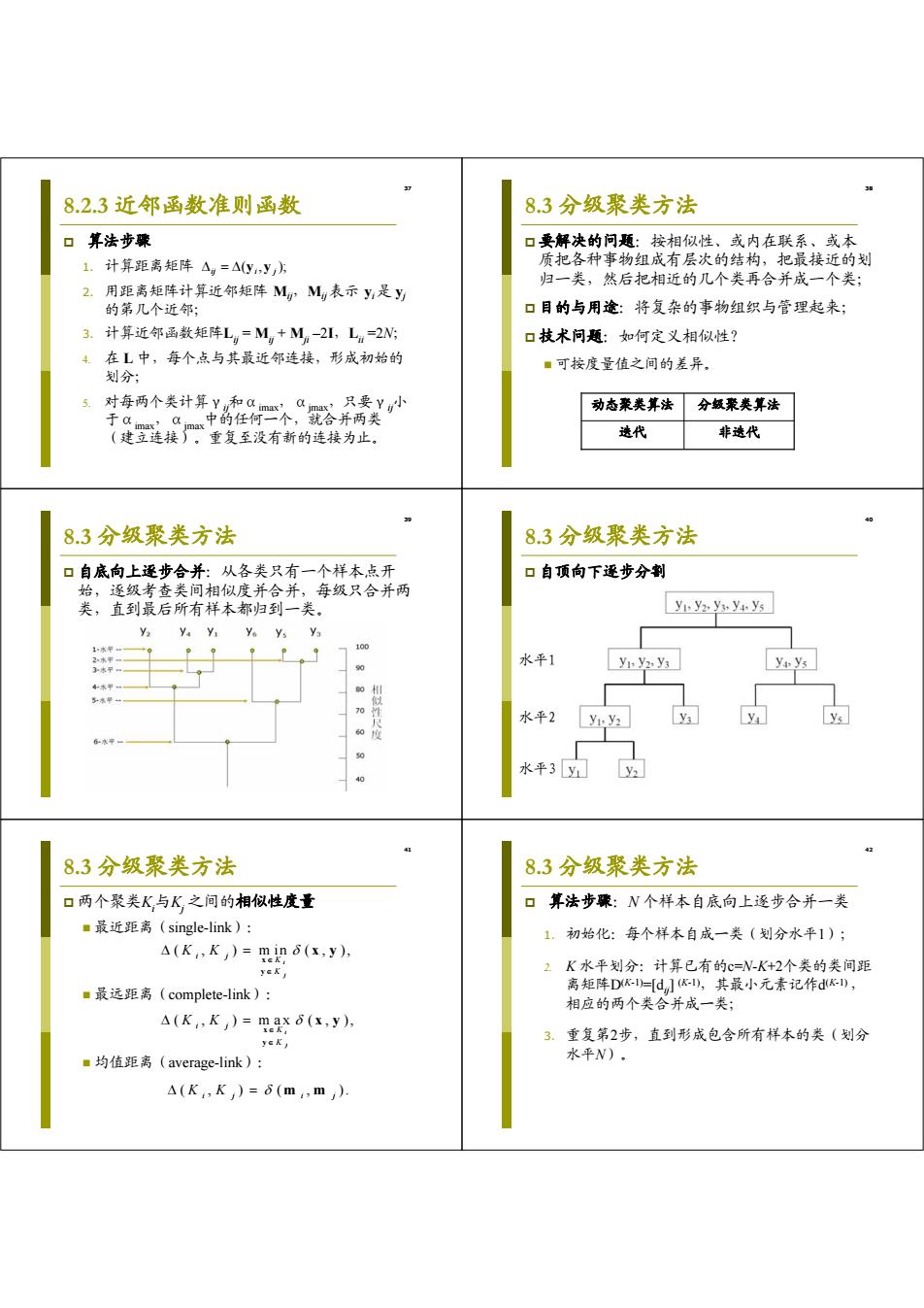
37 8.2.3 近邻函数准则函数  算法步骤 1. 计算距离矩阵 2. 用距离矩阵计算近邻矩阵 Mij，Mij表示 yi 是 yj 的第几个近邻； 3. 计算近邻函数矩阵Lij = Mij + Mji –2I，Lii =2N； 4. 在 L 中，每个点与其最近邻连接，形成初始的 划分； 5. 对每两个类计算γij和αimax，αjmax，只要γij小 于αimax，αjmax中的任何一个，就合并两类 （建立连接）。重复至没有新的连接为止。 ( , ); ij   yi y j 38 8.3 分级聚类方法  要解决的问题：按相似性、或内在联系、或本 质把各种事物组成有层次的结构，把最接近的划 归一类，然后把相近的几个类再合并成一个类；  目的与用途：将复杂的事物组织与管理起来；  技术问题：如何定义相似性？  可按度量值之间的差异。 迭代 非迭代 动态聚类算法 分级聚类算法 39 8.3 分级聚类方法  自底向上逐步合并：从各类只有一个样本点开 始，逐级考查类间相似度并合并，每级只合并两 类，直到最后所有样本都归到一类。 40 8.3 分级聚类方法  自顶向下逐步分割 水平1 水平2 水平3 41 8.3 分级聚类方法  两个聚类Ki 与Kj 之间的相似性度量  最近距离（single-link）：  最远距离（complete-link）：  均值距离（average-link）： ( , ) m in ( , ), i j i j K K K K      x y x y ( , ) m ax ( , ), i j i j K K K K      x y x y ( , ) ( , ). K K ij i j    m m 42 8.3 分级聚类方法  算法步骤：N 个样本自底向上逐步合并一类 1. 初始化：每个样本自成一类（划分水平1）； 2. K 水平划分：计算已有的c=N-K+2个类的类间距 离矩阵D(K-1)=[dij] (K-1)，其最小元素记作d(K-1) ， 相应的两个类合并成一类； 3. 重复第2步，直到形成包含所有样本的类（划分 水平N）

8.3分级聚类方法 8.3分级聚类方法 口不同相似性度量对结果的影响 口不同相似性度量对结果的影响 se减 Single-Link Method ab c d Complete-Link Method Complcte-Link Euclidean Distance Euclidean Distance ab cd 2) (3) ) (2) Distance Matrix Distance Matrix 8.3分级聚类方法 8.4非监督学习方法中的一些问题 口不同相似性度量对结果的影响 口非监督模式识别问题存在更大的 不确定性：可利用信息少 ■相似性度量一般对数据尺度(scale) 较敏感； 88g。。8 口影响聚类结果的因素：样本的分 布，样本数量，聚类准则，相似 。 性度量，预分类数等； 0 口针对不同数据，不同目标选择不 同的聚类算法； 口动态聚类算法计算效率高，实际 果利道即离香为标白作皮量 星尾罐事奔作为相点性度营 应用多

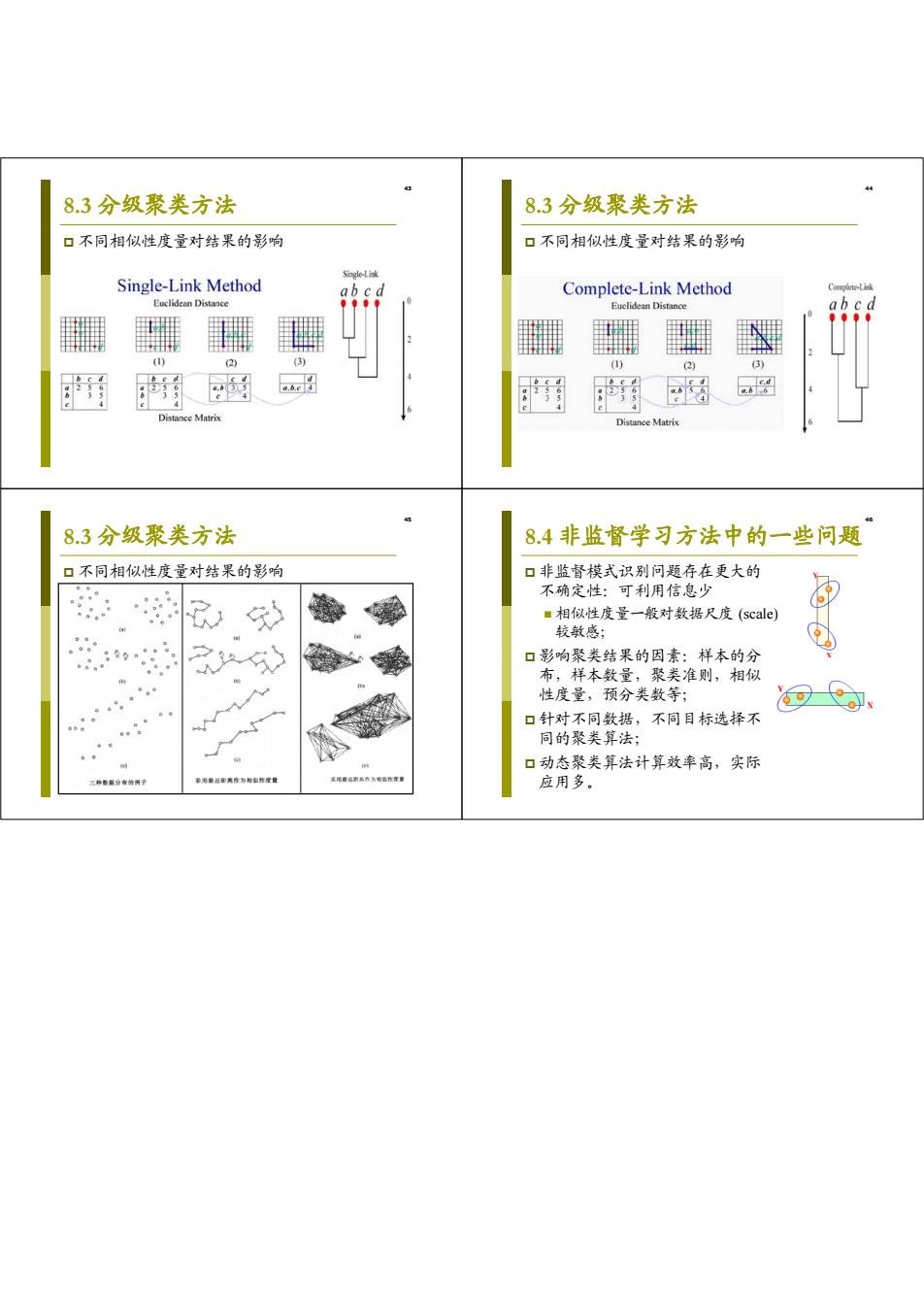
43 8.3 分级聚类方法  不同相似性度量对结果的影响 44 8.3 分级聚类方法  不同相似性度量对结果的影响 45 8.3 分级聚类方法  不同相似性度量对结果的影响 46 8.4 非监督学习方法中的一些问题  非监督模式识别问题存在更大的 不确定性：可利用信息少  相似性度量一般对数据尺度 (scale) 较敏感；  影响聚类结果的因素：样本的分 布，样本数量，聚类准则，相似 性度量，预分类数等；  针对不同数据，不同目标选择不 同的聚类算法；  动态聚类算法计算效率高，实际 应用多