
Bubble growth and collapse
Bubble growth and collapse

Introduction Gas bubbles can grow or collapse in flow Introducing many important phenomena General assumptions in this chapter Flow far away from bubble is at rest -Spherical symmetric bubble Single bubble
Introduction • Gas bubbles can grow or collapse in flow • Introducing many important phenomena • General assumptions in this chapter – Flow far away from bubble is at rest – Spherical symmetric bubble – Single bubble

Rayleigh-Plesset equation Looking for a function for bubble radius R(t) ·Assumptions: Liquid temperature Too constant Liquid pressure Po()is a known input Liquid density pL constant Liquid viscosity constant and uniform Bubble is homogeneous,Ta(t)and pE()are uniform
Rayleigh-Plesset equation • Looking for a function for bubble radius • Assumptions: – Liquid temperature constant – Liquid pressure is a known input – Liquid density constant – Liquid viscosity constant and uniform – Bubble is homogeneous , and are uniform

Rayleigh-Plesset equation 。Conservation of mass -4(,)=F F()related to boundary condition of bubble -On the bubble surface,u(R,t)=dR/dt -good for vapor density is much smaller u(r,t) LIQUID p(r,t) FAR FROM BUBBLE T(r,t) Poo(t],Too ∠-R(t)+ VAPOR GAS Pe(t).Te(t] -BUBBLE SURFACE
Rayleigh-Plesset equation • Conservation of mass – related to boundary condition of bubble – On the bubble surface, – , good for vapor density is much smaller

Rayleigh-Plesset equation N-S equation in r direction 1∂p0u,0u pLar=t+“ar {品 ·Introducing u=F(t)/r2 1 Op 1 dF 2F2 PL Orr2 dt r5 ·Integrate to get p-Poo 1dF 1F2 PL r dt 2r4 Net force on the surface radially outward 2S (Orr)r=R+PB-R Orr =-p+2uLou/Or. AuL dR PB -(p)r-R-R dt 2S replacing (p),=R R pB(t)-p∞() d2R 3 dR 2 AvL dR 2S PL -2 dt R dt PLR
Rayleigh-Plesset equation • N-S equation in r direction • Introducing • Integrate to get • Net force on the surface radially outward • replacing

Bubble content effect Assume bubble contains non-condensable gas Partial pressure poo at reference size and temp. pa)=ma+o(是)(货) Te need to be determined,rewrite the R-P equation: pv(T)-Poe(t)pv(TB)-pv(To) PL PL ()() d2R 3 dR AvL dR 2S =R d2+2( +R dt PLR First term is driving term Thermal term,which is considered later
Bubble content effect • Assume bubble contains non-condensable gas – Partial pressure at reference size and temp. • TB need to be determined, rewrite the R-P equation: – First term is driving term – Thermal term, which is considered later

Bubble content Taylor expansion on the first term Pv(TB)-PV(Too)=A(TB-Too) PL -A can be derived from Clausius-Clapeyron relation A=1= Pv(To)L(Too) PL dT PLToo 。Determine(Ts-To) -First step:heat diffusion equation,relates (Ta-T(ar/an +()买-是() Second step:energy balance,relates (aT/ar),-R R(t). dR kL dt PyC r-R (TB-Too) R(t)
Bubble content • Taylor expansion on the first term – A can be derived from Clausius-Clapeyron relation • Determine – First step: heat diffusion equation, relates – Second step: energy balance, relates

Bubble content However,the heat diffusion equation is hard to solve analytically Approximated solution for RT。-IB(器)),R mo-()/r盟 du -Using results from former 人) [R(x)2 dx [fR4(g)d划 It can introduce to R-P equation
Bubble content • However, the heat diffusion equation is hard to solve analytically • Approximated solution – for – Using results from former – It can introduce to R-P equation

Bubble content Focusing on bubble size change,then R=Rt" R*and n are constants. 。Former equation T。-TBd=CovR--iCm) PLCPLD ca=n)产f Thermal term (Ta-T)t--(Ts )C(n) PLToo C2py ∑(T)= PiePLTooDE
Bubble content • Focusing on bubble size change, then • Former equation Thermal term
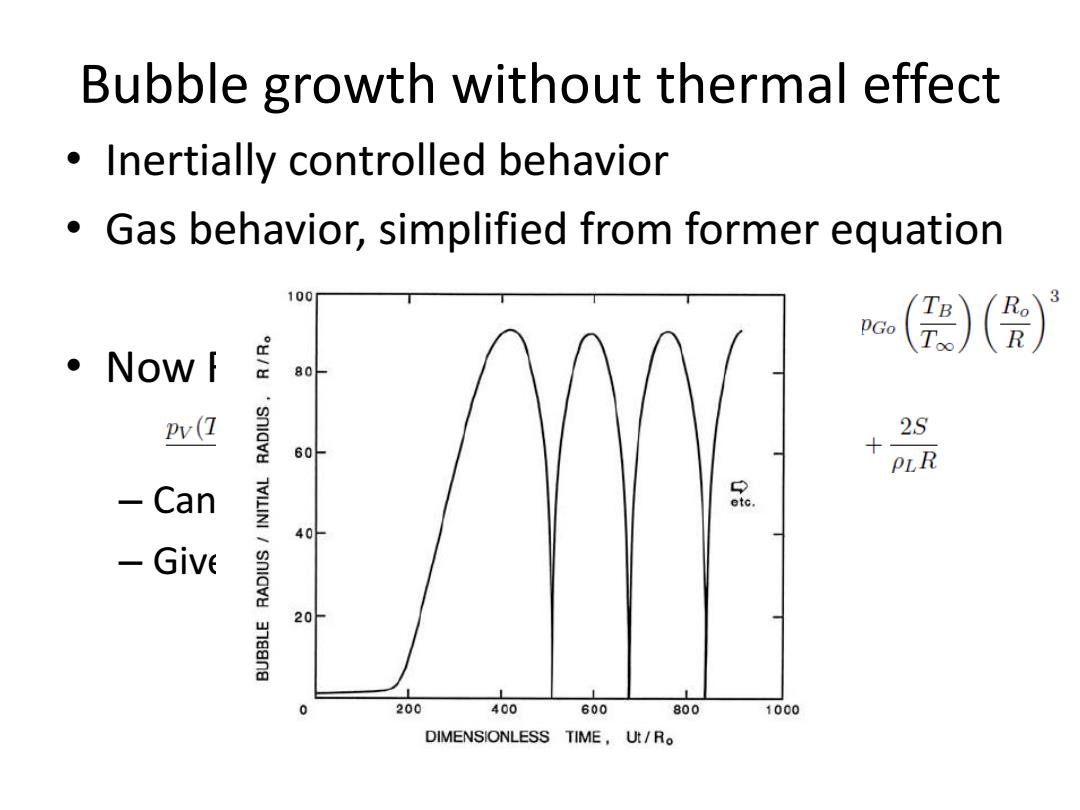
Bubble growth without thermal effect Inertially controlled behavior Gas behavior,simplified from former equation 100 ()() ·NoWf 80 Pv(1 2S 60 PLR Can etc. 40 -Give 20- 0 200 400 600 800 1000 DIMENSIONLESS TIME,U/R
Bubble growth without thermal effect • Inertially controlled behavior • Gas behavior, simplified from former equation • Now R-P equation – Can be solved numerically – Given constants and initial conditions