
CHAPTER 3.THE VAPOR COMPRESSION CYCLE 3.The vapor compression cycle* A.Introduction and fundamental concepts A1.First and second laws of thermodynamics 3.01 The purpose of refrigeration is to reduce and maintain the temperature of a substance below the temperature of the surroundings. To accomplish this,heat must be conveyed from a lower temperature source (the substance)to a higher temperature sink(the surroundings).This,however,must be done under the constraints of the second law of thermodynamics:It is impossible for any system to operate in a cycle in such a way that the sole result would be a heat transfer from a cooler to a hotter body.Therefore,such a heat conveyance is possible only if work (or,more generally,exergy)is supplied to the system. To reach this goal we have to use a cycle operating between the lower,desired, temperature and the higher temperature prevailing in the ambient or in available cooling water. This type of cycle also is used in heat pumps.The purpose of a heat pump is to extract heat from a lower temperature source and reject heat to a higher temperature sink at a useful level.The only difference between a refrigeration system and a heat pump lies in the choice of temperature levels.In the simple cases,a refrigeration system rejects heat to the surroundings,while a heat pump extracts heat from the surroundings. According to the first law of thermodynamics,the heat O rejected from the cycle at the higher temperature is equal to the sum of the heat 2 extracted at the lower temperature and the work E(or,more generally,the energy)necessary to operate the cycle,Figure 3.01,i.e. High temperature heat sink g Refrigeration system E or Heat pump 0 Low temperature heat source Fig.3.01.Principle of refrigeration systems and heat pumps. Authors:Ingvar Ekroth(Sections:Aand B):Eric Granryd (Section C) 3:1

REFRIGERATING ENGINEERING O1=02+E 3.01 The net energy input E,which is required to lift the heat O2 from the lower to the higher temperature,need not necessarily be mechanical work.For example in an absorption refrigeration system heat from a high temperature source is used to operate the cycle, and in an ejector(vacuum)refrigeration system kinetic energy is used. A2.Carnot cycle 3.02 Theoretically,among many other possibilities,we can make use of the reversible Carnot cycle.As Figure 3.02 depicts,the cycle is operated in the anti-clockwise direction between the temperatures T2 and T1.The working fluid executes four reversible processes in the cycle: T E a b Fig.3.02.The Carnot cycle in a temperature-entropy (T-s)diagram. a>b:isothermal expansion at T2 while heat 2 is transferred to the working fluid from the heat source b->c:isentropic compression from T2 to Ti without any heat transfer c->d:isothermal compression at Ti while heat O is transferred from the working fluid to the heat sink d>a:isentropic expansion from Ti to T2 without any heat transfer. The net work input supplied to the working fluid during the cycle is denoted E,and the first law of thermodynamics,Equation 3.01,gives E=O1-O2. A3.Principle of the vapor compression cycle 3.03 In actual applications of refrigeration,cycles operated with mechanical work are predominant.All vapor compression systems function in that way. The working fluid in a vapor compression system is called a refrigerant.In this introductory chapter the discussions are restricted to cycles operating with refrigerants 3:2
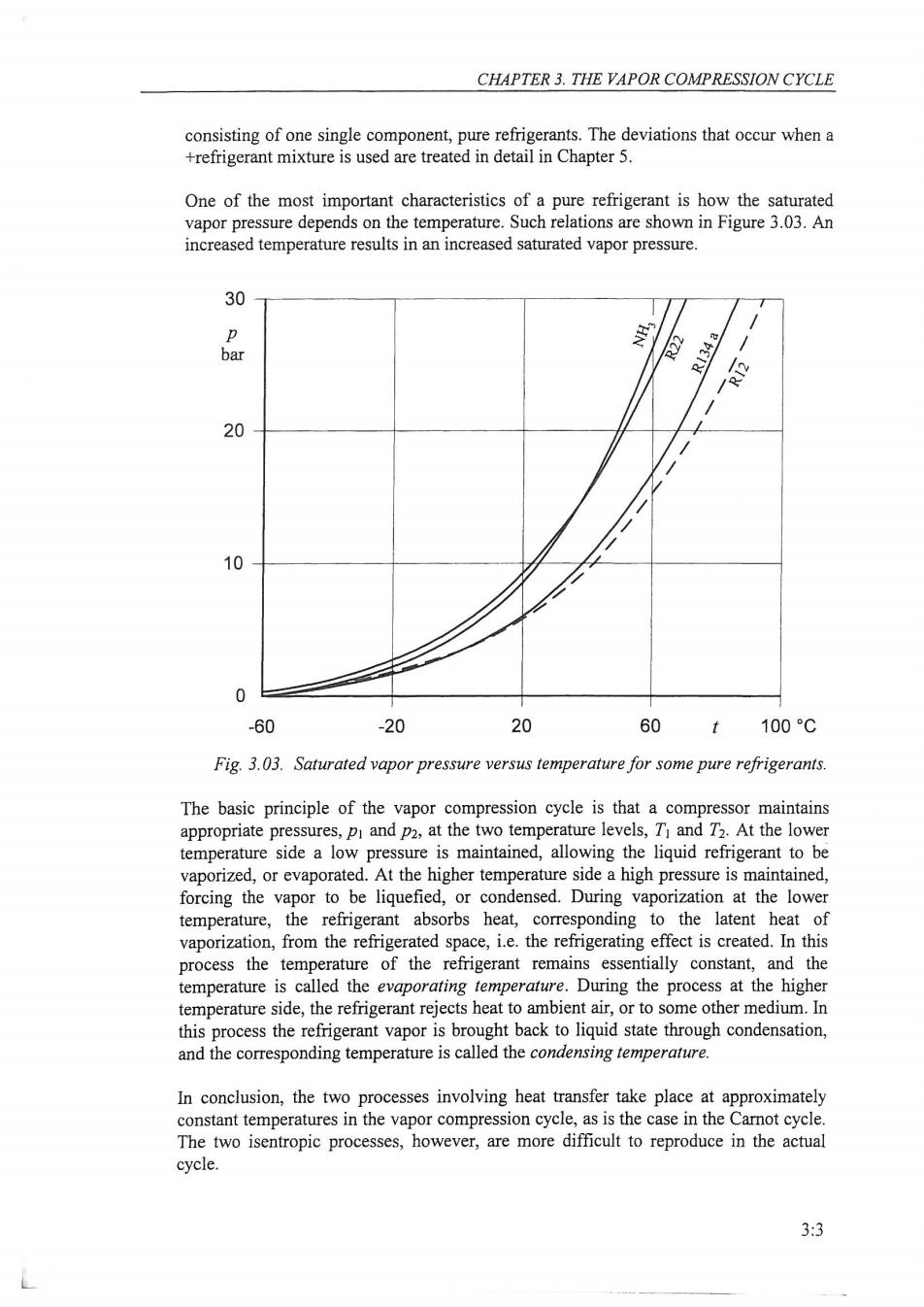
CHAPTER 3.THE VAPOR COMPRESSION CYCLE consisting of one single component,pure refrigerants.The deviations that occur when a +refrigerant mixture is used are treated in detail in Chapter 5. One of the most important characteristics of a pure refrigerant is how the saturated vapor pressure depends on the temperature.Such relations are shown in Figure 3.03.An increased temperature results in an increased saturated vapor pressure. 30 p NH: bar R134a e 20 10 0 -60 -20 20 60 t 100C Fig.3.03.Saturated vapor pressure versus temperature for some pure refrigerants. The basic principle of the vapor compression cycle is that a compressor maintains appropriate pressures,pi and p2,at the two temperature levels,T and T2.At the lower temperature side a low pressure is maintained,allowing the liquid refrigerant to be vaporized,or evaporated.At the higher temperature side a high pressure is maintained, forcing the vapor to be liquefied,or condensed.During vaporization at the lower temperature,the refrigerant absorbs heat,corresponding to the latent heat of vaporization,from the refrigerated space,i.e.the refrigerating effect is created.In this process the temperature of the refrigerant remains essentially constant,and the temperature is called the evaporating temperature.During the process at the higher temperature side,the refrigerant rejects heat to ambient air,or to some other medium.In this process the refrigerant vapor is brought back to liquid state through condensation, and the corresponding temperature is called the condensing temperature. In conclusion,the two processes involving heat transfer take place at approximately constant temperatures in the vapor compression cycle,as is the case in the Carnot cycle. The two isentropic processes,however,are more difficult to reproduce in the actual cycle. 3:3

REFRIGERATING ENGINEERING 3.04 The basic configuration of vapor compression systems includes an evaporator,a compressor,a condenser,and an expansion device.Additional items are a refrigerant, pipings,and a motor to operate the compressor.The equipment diagram for a simple vapor compression system is shown in Figure 3.04.The refrigerant circulates in the closed loop formed by the four main components and is subject to the four processes evaporation,compression,condensation,and throttling. high pressure side condenser low pressure side expansion device compressor a evaporator 个92 refrigerated space Fig.3.04.Equipment diagram for a simple vapor compression system. A4.Energy equation and property diagrams 3.05 The cycle executed by the refrigerant in a vapor compression system can readily be studied in a thermodynamic property diagram for the refrigerant.There are many different types of such diagrams.Here we are going to make use of the temperature- entropy (T-s)diagram and the pressure-enthalpy (p-h)diagram.The p-h diagram is widely used in the refrigeration field.It has a linear scale for the enthalpy and a logarithmic scale for the absolute pressure and is frequently called a log(p)-h diagram. The fundamental theory and concepts of the diagrams are known from the course in thermodynamics and will not be repeated here. However,for the purpose of reference,we will give the energy equation for a control volume at steady state flow.The general form,valid for both reversible and irreversible processes,on a per unit mass basis is g=a+h2-h1+(w22-w1)/2+g(22-z1) 3.05a This equation is applicable to each component in the vapor compression system shown in Figure 3.04.The indices 1 and 2 denote the inlet state and outlet state,respectively, for the working fluid and are replaced by the appropriate notations(a,b,c,and/or d)for the component to be studied. 3:4

CHAPTER 3.THE VAPOR COMPRESSION CYCLE In the equation q net amount of heat transferred to the working fluid =net amount of shaft work delivered from the working fluid h specific enthalpy for the working fluid w=velocity of the working fluid z elevation above an arbitrarily datum level g =acceleration due to gravity. In vapor compression systems,changes in the potential energy (gz)are mostly negligible,and so are normally changes in the kinetic energy(w/2),leaving the energy equation in the simple form q=a+h2-h 3.05b Important notice:Heat transfer and work per unit mass exposed to a process are designated by the lower-case letters g and &respectively.The unit for g and eis J/kg or kJ/kg.The total amount of heat transfer and work in J or kJ are designated by the capital letters O and E,and are obtained from g and &by multiplication with the mass m in kg involved in the process,e.g.O=m.q.The corresponding rates of energy transfer in W or kW are symbolized by a dot,i.e.Oand E,and the multiplication is now with the mass flow rate m in kg/s,e.g.Q=mq.(Later on,in sections 3.30 and 3.32,two volumetric quantities gv and in J/m'or kJ/m'are introduced.) B.Simple vapor compression cycle B1.The simple cycle in T-s and p-h diagrams 3.06 Figure 3.06 shows the cycle for a simple vapor compression system according to Figure 3.04 in T-s and p-h diagrams.As explained previously,the main part of the cycle is executed in the wet region(also called the liquid-vapor saturation region,the two-phase region or the vapor dome),where the refrigerant undergoes vaporization and condensation.The compressor and the expansion device maintain a high pressure side, with the pressure pi,and a low pressure side,with the pressure p2.The corresponding condensing temperature and evaporating temperature are denoted Ti and T2, respectively. 3.07 The evaporator is a container or a pipe system wherein the refrigerant vaporizes at a low temperature.The latent heat of vaporization is taken from the surroundings of the evaporator,in this case the air in a refrigerated space.Heat is removed from that space and the temperature in the space is kept at a low,desired,level. The compressor sucks away the formed vapor,thereby keeping the pressure at a low level,allowing the vaporization to be maintained.To make the heat transfer possible, from the air in the refrigerated space to the refrigerant,the boiling temperature of the refrigerant,i.e.the evaporating temperature,has to be below the temperature of the air in the refrigerated space. 3:5

REFRIGERATING ENGINEERING p C d T T P 6 T P2 a a ha=h。=h 92 9 h 片 h h2 hax k Fig.3.06.The simple cycle in T-s and p-h diagrams. The pressure in the evaporator is called the evaporating pressure.For a pure refrigerant, a certain evaporating pressure corresponds to a specific evaporating temperature according to the vapor pressure curve,the relation between saturated vapor pressure and temperature.Figure 3.03 illustrates this relation for some refrigerants. For example with ammonia,NH3,as the refrigerant,and presuming that the compressor maintains the evaporating pressure equal to 2,9 bar,then the evaporating temperature will be-10C.The evaporating temperature will decrease if the evaporating pressure is depressed. Under steady-state conditions,the evaporator is supplied with a continuous flow of refrigerant which is vaporized successively by the heat transferred from the refrigerated space.The pressure drop in the flow direction of the refrigerant is normally small and, consequently,the heat transfer to the refrigerant takes place under essentially constant pressure and constant temperature. In the evaporator it is a constant-pressure,almost constant-temperature process, indicated by the line a-b in the diagrams.At the inlet to the evaporator,point a,the refrigerant consists of a mixture of saturated liquid and saturated vapor having the average enthalpy hs.Heat transfer from the refrigerated space causes the liquid to evaporate and change the mixture of liquid and vapor into a saturated vapor.In practice, however,the cold vapor usually will continue to absorb heat from the refrigerated space and become slightly superheated before it leaves the evaporator.At the outlet,point b, the enthalpy is hak. According to the energy equation,Equation 3.05b,with=0 for the evaporator,the refrigerating effect (in Swedish koldalstring)is 92=h2k-hs 3.07a 3:6

CHAPTER 3.THE VAPOR COMPRESSION CYCLE The refrigerating effect g2 is the quantity of heat that each unit mass of refrigerant absorbs from the refrigerated space.The unit for the refrigerating effect is the same as for the enthalpy,i.e.J/kg or kJ/kg If the mass flow rate of the refrigerant is denoted m (in kg/s)then the refrigerating capacity (in Swedish kyleffekt)(in W or kW)is Q=m(hak-hs) 3.07b The vapor is conveyed to the suction inlet of the compressor through the suction line,or the low-pressure line. 3.08 The compressor might be one of several types,e.g.reciprocating,rotary,scroll,screw, or centrifugal compressor.The purpose of the compressor is to remove the vapor from the evaporator and force it into the condenser.The compressor maintains such a low pressure in the evaporator so as to enable the refrigerant to vaporize,and at the same time maintain such a high pressure in the condenser as to allow the refrigerant to condense at the temperature prevailing there.The work input to the refrigerant in the compressor makes it possible to lift the heat absorbed in the evaporator to a higher temperature level,where the heat can be rejected to ambient air or to cooling water. The compressor creates the necessary pressure difference and together with the expansion device it maintains that difference between the low pressure side and the high pressure side of the cycle. The process in the compressor might often be considered as adiabatic,with no heat transfer.The work is commonly supplied by an electric motor,although internal combustion engines (especially in systems for automobile air-conditioning),steam engines,and steam turbines are sometimes used. The refrigerant enters the compressor as a slightly superheated vapor,point b.In the theoretical cycle the compression process is assumed to be isentropic,presupposing negligible heat exchange with the surroundings.In an isentropic process the entropy s is constant and the line b-cis coincides with a line of constant entropy,starting at point b and ending at the condensing pressure pi,point cis.Since work is done on the vapor during the compression,the enthalpy of the refrigerant is increased from hak to hIk is, theoretically.From the energy equation,Equation 3.05b,the required work of isentropic compression on a per unit mass basis is Ed=h1k.is -h2k 3.08a where the index d denotes that the values are ideal,from the diagram. With the mass flow rate m,the power needed to operate an isentropic compressor is 店=ia 3.08b 3:7

REFRIGERATING ENGINEERING In reality,additional work is required to compensate for mechanical friction,fluid friction,and other losses in the compressor.Let us define a total isentropic compression efficiency as mk =Edl ak or ak=Edl mk 3.08c where a is the actual work that must be supplied to the shaft of the compressor. Hence the actual compressor power is 民=i/Tk 3.08d The efficiency nk often is in the range 0,6-0,8,and with an adequate knowledge of the magnitude in an actual case,the outlet state c from the compressor can be established when the inlet state b is known. It is often of interest to calculate the outlet conditions from the compressor.If the compressor operates adiabatically,i.e.without any heat transfer to or from the sur- roundings,we have hik=hak +a or hik=h2k+&m 3.08e where hik is the enthalpy of the refrigerant at the true outlet state from the compressor. Combining this with Equation 3.08a we can also write hik =h2k +(hik.is -h2k)/m 3.08f If the compressor is non-adiabatic,i.e.some heat transfer occurs,the Equations 3.08c-f must be modified according to Equation 3.05b. The discharge line,or the hot gas line,delivers the high pressure,high temperature vapor from the compressor to the condenser. 3.09 The condenser might be air cooled or water cooled or a combination thereof.The refrigerant condenses in the condenser.The pressure of the vapor will be so high that the available cooling medium can be used to bring the vapor to condensation.To enable this heat transfer,from the refrigerant to the cooling medium,the condensing temperature must be higher than the temperature of the cooling medium.With the relation between saturated vapor pressure and temperature,Figure 3.03,it is possible to determine the necessary condensing pressure. For example if the condensing temperature is supposed to be +30C,using ammonia as the refrigerant,the compressor has to maintain a pressure equal to 11,7 bar in the condenser. 3:8

CHAPTER 3.THE VAPOR COMPRESSION CYCLE As in the evaporator,the process in the condenser takes place under almost constant pressure.Even though the vapor at the condenser inlet often might be considerably superheated,the main part of the heat rejection occurs at a constant temperature,i.e.the condensing temperature. The heat O rejected from the condenser to the cooling medium equals to the sum of the heat 2 extracted from the refrigerated space and the work Ek supplied to the refrigerant in the compressor,i.e.1=2+Ek. The process in the condenser takes place at constant pressure as shown by the line c-d. In most cases,the gas discharged from the compressor is a superheated vapor,i.e.the hot gas temperature,in point c,is above the condensing temperature Ti as indicated in the diagrams.This superheated vapor is cooled to the condensing temperature in the entrance part of the condenser,then condensation takes place at a constant temperature to the saturated liquid state.The sensible heat connected to the superheat as well as the latent heat released during the condensation are rejected from the refrigerant in the condenser.Often it is possible to cool the warm liquid refrigerant to a temperature below the condensing temperature.This liquid subcooling takes place through further heat rejection at the end of the condenser or in a special liquid subcooler resulting in the liquid temperature Ts,in point d. The energy equation gives for the condenser(including liquid subcooler if any)that the rejected heat on a per unit mass basis is gi=hik-hs 3.09a With the mass flow rate m of the refrigerant,the condenser load is e=m(hik-hs) 3.09b This expression is equivalent to ②=92+Ek 3.09c where =the refrigerating capacity Er=the power input to the refrigerant during the compression. Equation 3.09c is in harmony with the general Equation 3.01. The liguid line carries the liquid refrigerant from the condenser to the expansion device. 3.10 The expansion device is also called the refrigerant flow control.There are a number of different types of expansion devices available,e.g.a simple hand-operated expansion valve,the self-modulating thermostatic expansion valve,low and high pressure float valves,and the simple capillary tube. 3:9

REFRIGERATING ENGINEERING The purpose of any expansion device is twofold: to accomplish the throttling process and maintain the pressure difference between the condenser and the evaporator to adjust the refrigerant flow rate to the evaporator;keeping the evaporator filled with refrigerant liquid,yet preventing the liquid to be carried over to the compressor where it might cause damages through liquid hammer. By this uncomplicated expansion device,the pressure as well as the temperature can be reduced from the level existing in the condenser (including subcooler)to the level wanted in the evaporator. As mentioned earlier,the cycle has a high pressure side and a low pressure side,and the boundary line is at the expansion device and the compressor. The entire heat extraction,i.e.the refrigerating effect,occurs on the low pressure side of the cycle,and the heat rejection takes place on the high pressure side. The process in the expansion valve completes the cycle.Here a throttling process takes place and we obtain the well known condition that the enthalpy of the refrigerant has the same value before and after the reduction of the pressure.This relation is readily obtained from the energy equation,Equation 3.05b,with q=0 and &=0,leaving ha=ha 3.10 Such a process is usually referred to as a throttling process.The thermodynamic state at the outlet of the expansion valve,i.e.the inlet to the evaporator,is located in the diagram by following the line of constant enthalpy from point d to the intersection with the line representing the evaporating pressure,point a. The pressure of the refrigerant is reduced in the throttling process and the liquid begins to vaporize,and a portion of the liquid turns into vapor.This portion must be supplied with the latent heat of vaporization.This energy is taken from the fluid itself,resulting in a reduction of the temperature,from Ts to T2.The low temperature of the cycle is created in the expansion device! Normally,the expansion valve is installed close to the evaporator,and when the refrigerant passes through the valve,we have completed one loop of the cycle,and the course of events will repeat again. (Equation 3.10 does not hold for one of the most frequent applications,namely household refrigerators.These domestic units are usually equipped with a capillary tube where the refrigerant in the expansion process is brought into heat exchange with the vapor leaving the evaporator.To analyze this we have to apply Equation 3.05b and the situation resembles that which is treated in sections 3.41-42.) 3.11 State point a represents a mixture of saturated liquid,at state a',and saturated vapor,at state a".Calculations on thermodynamic properties of such mixtures are strongly simplified through the introduction of the concept quality of the mixture,defined as the 3:10