
Single particle motion
Single particle motion

Assumption ·Dilute two phase flow -Solve continuous phase u and P ignoring dispersed phase. 。Normal approach Force balance Fi to mpdVi/dt Problem with fluid acceleration Start with following equations 0i=0 8xi +}- 825 Oppcvcj 8xi Rectilinear relative motion
Assumption • Dilute two phase flow – Solve continuous phase u and P ignoring dispersed phase. • Normal approach – Force balance Fi to mpdVi/dt – Problem with fluid acceleration • Start with following equations – Rectilinear relative motion

Flows around a sphere ·High Reynolds 卡品a+品 (ue sin)=0 +o{()+如。品 1 沿 2 0 2十r0r ue ue rug 10p PCa r80 + r r80 +ec{情品(r器)+ Sue 2 Our r2 sin20
Flows around a sphere • High Reynolds

Define stream fuction 10b 18p 4,=p2sin080 u8=一 rsine or For inviscid potential flow 2simn20-Psin20 Wr2 4,=-Wcos0- 2D T3 cos 0 D uo =+W sine-s sin D 6=-W'r cos+cose
• Define stream fuction • For inviscid potential flow
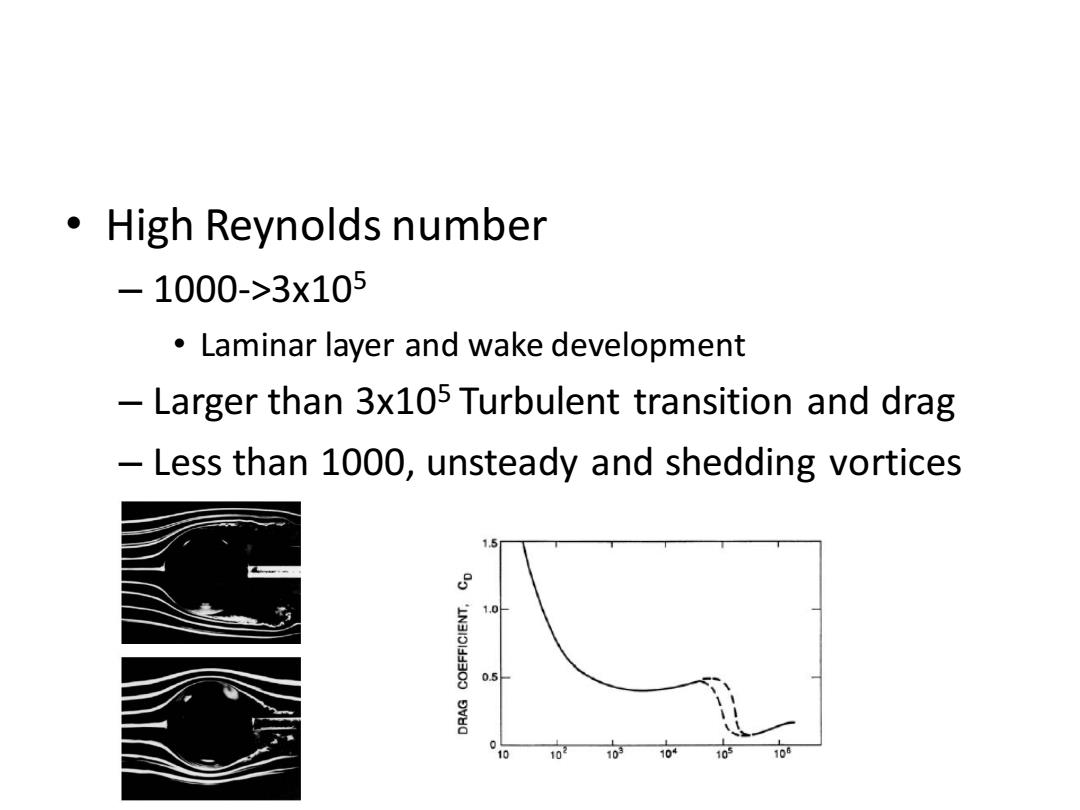
。High Reynolds number -1000->3x105 Laminar layer and wake development Larger than 3x105 Turbulent transition and drag Less than 1000,unsteady and shedding vortices 15 8 1.0 0.5 0 0 102 103 104
• High Reynolds number – 1000->3x105 • Laminar layer and wake development – Larger than 3x105 Turbulent transition and drag – Less than 1000, unsteady and shedding vortices

Low Reynolds Stokes flow Retain only viscous term in N-S equation =mo{"空+4+am} =m0{w+器+} o=-im{-w-号+}
• Low Reynolds – Stokes flow – Retain only viscous term in N-S equation

-Solution subcases ·Classic Stokes (U0)r=R=0 (Ur)r=R=0 A=- R3 ,B=+ 3WR 4 and F1=-6TPCVcWR 4 Hadamard zero shear stress A=0,B=+2 and F1=-4TPCVcWR ·Potential flow WR3 A=十 2 ,B=0 and F1=0 Further modification,to include effect from convection term, Oseen(no mirror symmetry,wake development) 8吃 W Di=1pC :0 0x1 pc Oxi =-wr{0+a9+rgt(-e》=-6eewa{+后} 2R2+ 。Proudman
– Solution subcases • Classic Stokes • Hadamard • Potential flow – Further modification, to include effect from convection term, • Oseen (no mirror symmetry, wake development) • Proudman

Flow with Re 0.5-couple thousand(experiment) Vortices develops at Re=30 Re increases and wake expands Re-130,wake reaches the particle size,begins oscillation Re-500,vortices begins to shed and convected to downstream Shedding frequency and Str Str =2fR/W Stable near-wake and a unstable,turbulent far-wake behind Re-1000,a flow around sphere and near-wake stable again,separates at 84 A=-6ewR+}
• Flow with Re 0.5-couple thousand(experiment) – Vortices develops at Re=30 – Re increases and wake expands – Re-130, wake reaches the particle size , begins oscillation – Re-500, vortices begins to shed and convected to downstream • Shedding frequency and Str • Stable near-wake and a unstable, turbulent far-wake behind – Re-1000, a flow around sphere and near-wake stable again, separates at 84°

Molecular effects Mean free path of the fluid molecules V.S.size Knudsen number Kn=λ/2R -A factor to Stokes drag (1+2AKn) 。Brownian motion -Diffusivity D=KT/6TucR Displacement Temperature gradient-thermophoresis -Radiation gradient-photophoresis Sound field-sonophoresis
Molecular effects • Mean free path of the fluid molecules V.S. size – Knudsen number – A factor to Stokes drag • Brownian motion – Diffusivity – Displacement • Temperature gradient- thermophoresis – Radiation gradient – photophoresis – Sound field- sonophoresis

Unsteady effect Particle is accelerating j F:=-Mij dt M-竖 volume uikujk d(volume) of fluid -Added mass matrix ·Symmetric Particle with plane symmetry will not experience force perpendicular to the plane -Difference with displaced mass (example,infinite thin plate) Real viscous application dvi 1 F:=-M -PcACulVV;
Unsteady effect • Particle is accelerating – Added mass matrix • Symmetric • Particle with plane symmetry will not experience force perpendicular to the plane – Difference with displaced mass (example, infinite thin plate) – Real viscous application