
北京航室航天大学 压缩感知概述 Introduction to Compressive Sensing
压缩感知概述 Introduction to Compressive Sensing
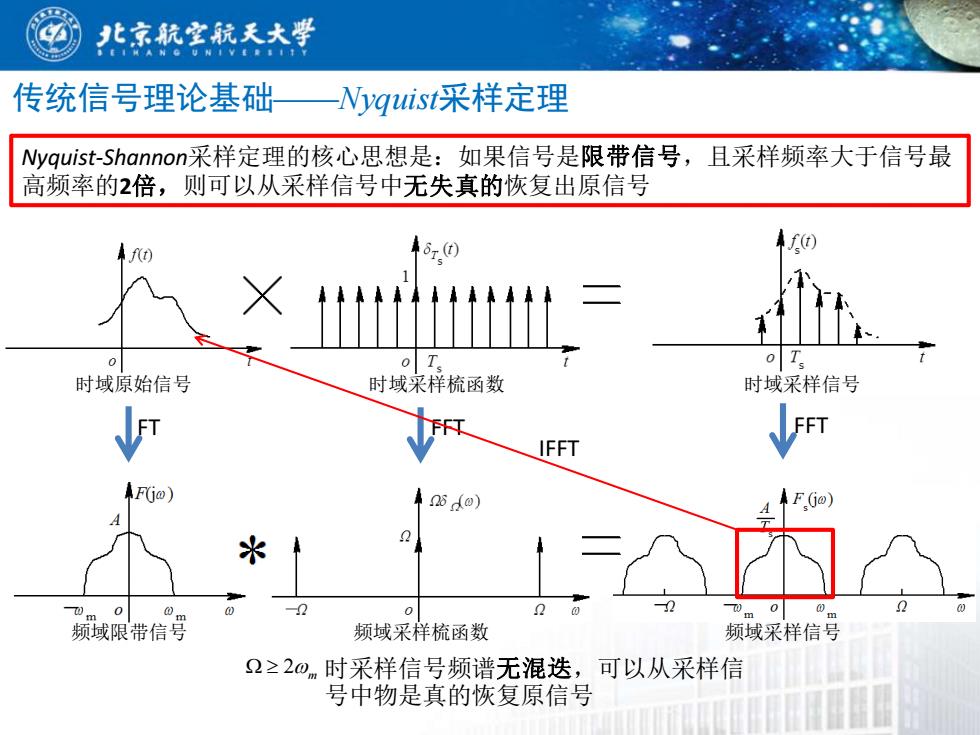
北京航室航天大学 传统信号理论基础 yquist采样定理 Nyquist--Shannon采样定理的核心思想是:如果信号是限带信号,且采样频率大于信号最 高频率的2倍,则可以从采样信号中无失真的恢复出原信号 f(t) oT. 时域原始信号 时域采样梳函数 时域采样信号 IFFT AF(jo) 年25o) 米 2 0 频域限带信号 频域采样梳函数 频域采样信号 2≥20m时采样信号频谱无混迭,可以从采样信 号中物是真的恢复原信号
传统信号理论基础——Nyquist采样定理 时域原始信号 时域采样梳函数 时域采样信号 频域限带信号 频域采样梳函数 频域采样信号 Nyquist-Shannon采样定理的核心思想是:如果信号是限带信号,且采样频率大于信号最 高频率的2倍,则可以从采样信号中无失真的恢复出原信号 2 m 时采样信号频谱无混迭,可以从采样信 号中物是真的恢复原信号 FT FFT FFT IFFT
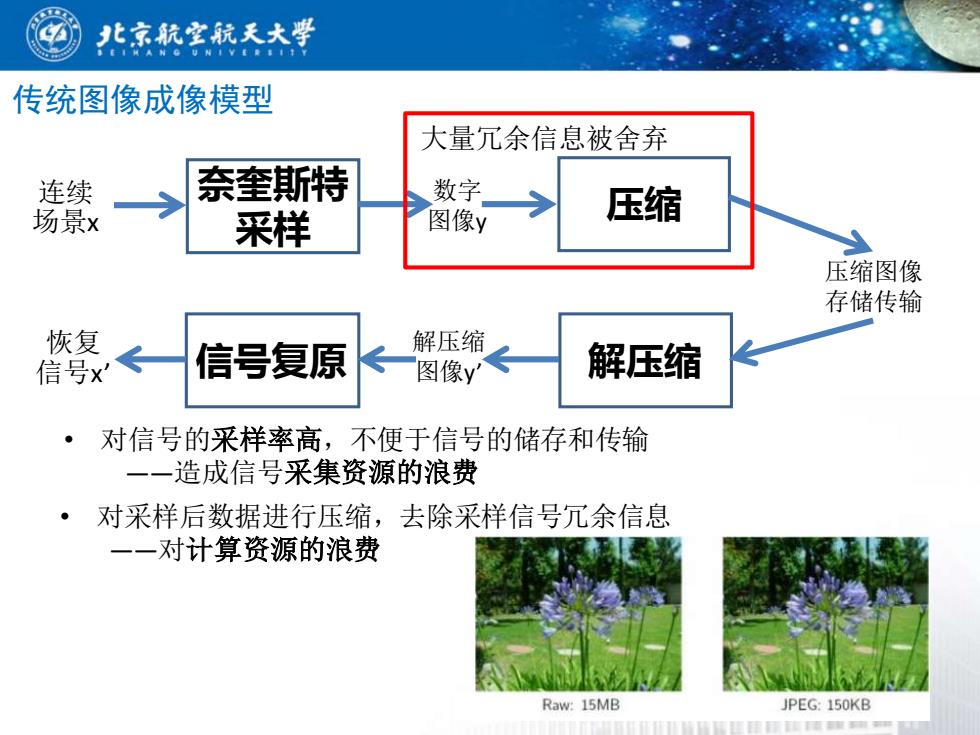
北京航室航天大学 传统图像成像模型 大量冗余信息被舍弃 连续 奈奎斯特 数字 场景x 采样 图像y 压缩 压缩图像 存储传输 恢复 信号复原 解压缩 信号x' 图像yS 解压缩 对信号的采样率高,不便于信号的储存和传输 一一造成信号采集资源的浪费 ·对采样后数据进行压缩,去除采样信号冗余信息 一一对计算资源的浪费 Raw:15MB JPEG:150KB
传统图像成像模型 奈奎斯特 采样 连续 场景x 压缩 解压缩 数字 图像y • 对信号的采样率高,不便于信号的储存和传输 ——造成信号采集资源的浪费 • 对采样后数据进行压缩,去除采样信号冗余信息 ——对计算资源的浪费 压缩图像 存储传输 解压缩 信号复原 图像y’ 恢复 信号x’ 大量冗余信息被舍弃

北京航空航天大学 压缩感知模型构想 奈奎斯特 无损恢复 采样 信号 是否可以以低于奈奎斯特频率对信号采样,同时精确恢复信号? 是否可以直接采集压缩信息并通过压缩信息恢复原信号? “感知”一一 连续 宽泛的理解 场景x 压缩感知 为对信号的采样 压缩数据 存储传输 “压缩” 恢复 在采样过程中对 场景x' 信号重构 压缩信号进行采样 ● 在信号采集过程中,,直接感知压缩后信息一一减少对计算资源的浪费 以远低于奈奎斯特采样频率对压缩信息迸行采样 减少对信号采集资源的浪费 (1)信号每一个采样包含信号全 局信息 (2)存在一种算法从压缩采样信 息精确恢复信号 Raw:15MB JPEG:150KB
压缩感知模型构想 • 在信号采集过程中,直接感知压缩后信息——减少对计算资源的浪费 • 以远低于奈奎斯特采样频率对压缩信息进行采样 ——减少对信号采集资源的浪费 连续 场景x 压缩感知 压缩数据 存储传输 信号重构 恢复 场景x’ • 是否可以直接采集压缩信息并通过压缩信息恢复原信号? 奈奎斯特 采样 无损恢复 信号 • 是否可以以低于奈奎斯特频率对信号采样,同时精确恢复信号? (1)信号每一个采样包含信号全 局信息 (2)存在一种算法从压缩采样信 息精确恢复信号 “感知”—— 宽泛的理解 为对信号的采样 “压缩”—— 在采样过程中对 压缩信号进行采样
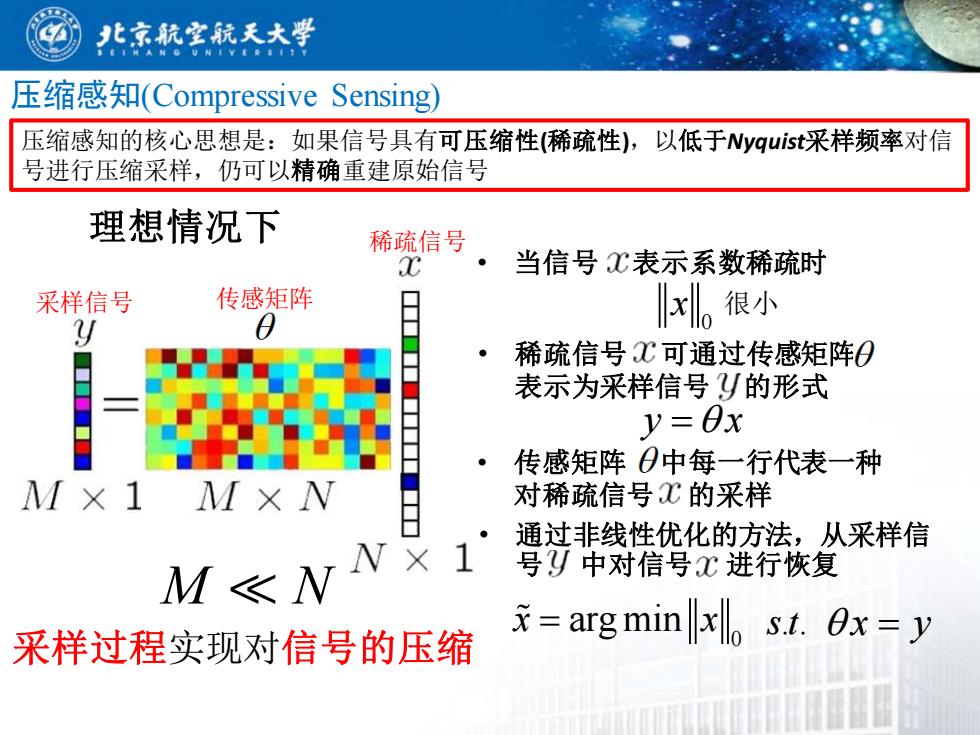
北京航字航天大臀 压缩感知(Compressive Sensing) 压缩感知的核心思想是:如果信号具有可压缩性(稀疏性),以低于Nyquist采样频率对信 号进行压缩采样,仍可以精确重建原始信号 理想情况下 稀疏信号。 C 当信号℃表示系数稀疏时 采样信号 传感矩阵 很小 稀疏信号C可通过传感矩阵0 表示为采样信号y的形式 y=0x 。 传感矩阵0中每一行代表一种 M×1M×N 对稀疏信号心的采样 M≤NNx1 通过非线性优化的方法,从采样信 号y中对信号℃进行恢复 采样过程实现对信号的压缩 x=argminx。st.Ox=y
压缩感知(Compressive Sensing) 压缩感知的核心思想是:如果信号具有可压缩性(稀疏性),以低于Nyquist采样频率对信 号进行压缩采样,仍可以精确重建原始信号 理想情况下 • 稀疏信号 可通过传感矩阵 表示为采样信号 的形式 y x = • 通过非线性优化的方法,从采样信 号 中对信号 进行恢复 0 x x = arg min st. . x y = 采样信号 传感矩阵 稀疏信号 • 传感矩阵 中每一行代表一种 对稀疏信号 的采样 M N 采样过程实现对信号的压缩 • 当信号 表示系数稀疏时 0 x 很小

北京航空就天大学 压缩感知(Compressive Sensing) 信号稀疏表示 自然信号℃的时域表示系数一 自然信号 稀疏基矩阵稀疏表示 般不是稀疏的 U a 自然信号化不满足压缩感知对 信号稀疏性的要求 自然信号C相对于稀疏基矩阵少 的表示系数Q是稀疏的 x=Ψa ·对信号C在稀疏基中的表示Q进行 N×1N×WN×1 恢复满足压缩感知对信号稀疏性的 要求 稀疏表示研究观测信号与稀疏信号的转化问题
压缩感知(Compressive Sensing) 信号稀疏表示 • 自然信号 的时域表示系数一 般不是稀疏的 自然信号 稀疏基矩阵 稀疏表示 • 自然信号 不满足压缩感知对 信号稀疏性的要求 • 自然信号 相对于稀疏基矩阵 的表示系数 是稀疏的 x = • 对信号 在稀疏基中的表示 进行 恢复满足压缩感知对信号稀疏性的 要求 稀疏表示研究观测信号与稀疏信号的转化问题

北京航室航天大学 自然信号 压缩感知(Compressive Sensing) 采样信号 测量矩阵 C ①D 测量矩阵 设计测量矩阵Φ对自然信号℃ 进行采样得到采样信号y 在确定信号的稀疏基业后 M×1 MXN 稀疏基矩阵信号的稀疏表示 N×1 a 采样信号 测量矩阵 ·可以将采样信号y 视为对自然信号℃ y 在变换域中稀疏表 示Q的采样 测量矩阵研究信对号 M×1M×N 进行压缩采样的问题 V×VV×1
压缩感知(Compressive Sensing) 测量矩阵 采样信号 测量矩阵 自然信号 • 设计测量矩阵 对自然信号 进行采样得到采样信号 • 在确定信号 的稀疏基 后 采样信号 测量矩阵 稀疏基矩阵 信号的稀疏表示 • 可以将采样信号 视为对自然信号 在变换域中稀疏表 示 的采样 测量矩阵研究信对号 进行压缩采样的问题

北京航空就天大学 压缩感知(Compressive Sensing) 稀疏基矩阵 信号恢复 传感矩阵 测量矩阵 ① 通过测量矩 阵中和稀 疏基矩阵Ψ 定义传感矩 阵日 MXN MX N 0=ΦΨ N×N稀疏信号 Q 通过非线性优化的方法,以及传感 采样信号 传感矩阵 矩阵日从采样信号y中对稀疏信 号Q进行恢复 a=arg minallo s.t.0a=y x=Ψa 中 传感矩阵研究从采样信号 M×1 M×N 到自然信号的求解问题
压缩感知(Compressive Sensing) 信号恢复 传感矩阵 测量矩阵 稀疏基矩阵 • 通过测量矩 阵 和稀 疏基矩阵 定义传感矩 阵 采样信号 传感矩阵 稀疏信号 • 通过非线性优化的方法,以及传感 矩阵 从采样信号 中对稀疏信 号 进行恢复 0 = arg min st. . = y = 传感矩阵研究从采样信号 到自然信号的求解问题 x =
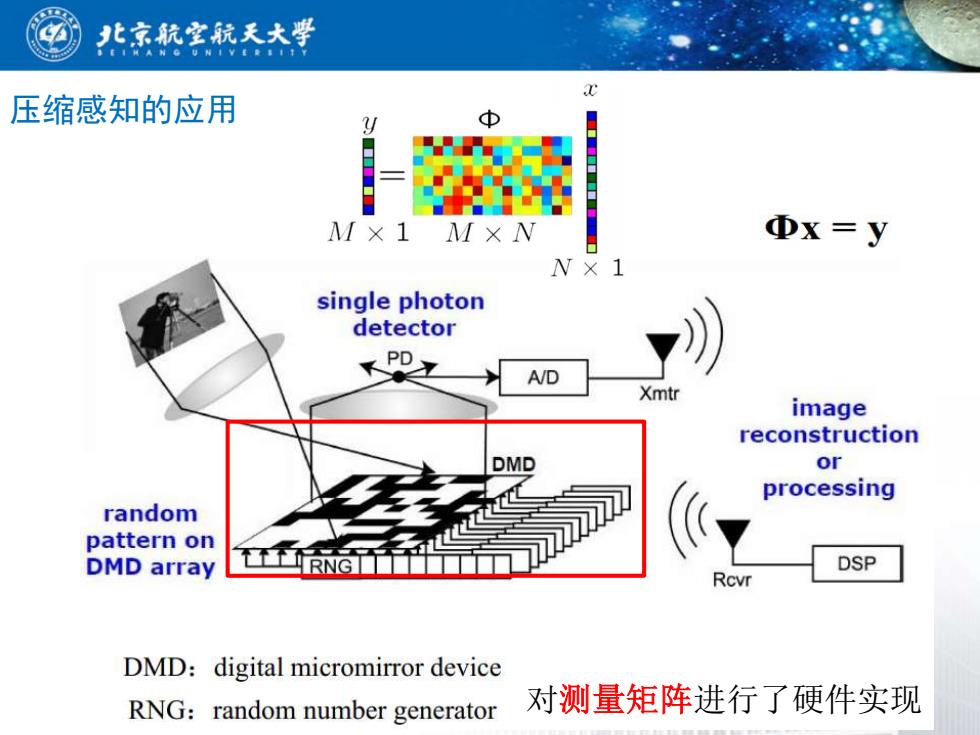
北京航室航天大学 压缩感知的应用 M×1M×N ΦX=y W×1 single photon detector : A/D Xmtr image reconstruction DMD or processing random pattern on DMD array DSP Rcvr DMD:digital micromirror device RNG:random number generator 对测量矩阵进行了硬件实现
压缩感知的应用 对测量矩阵进行了硬件实现

北京航室就天大学 从压缩感知到稀疏表示 ·假设原始高维信号为向量X,低维测量向量为y ·信号向量x与测量向量y满足线性组合关系A ·矩阵的压缩感知模型就是一个线性矩阵方程组 Ax=y 通过映射关系A获取高维信号X的低维采样y 如果原始信号向量x具有稀疏性 信号的稀疏度:信号中非零元素个数 minx。 信号稀疏度量:1°范数x。 s.t.Ax=y ·可以通过低维采样b对高维信号X进行恢复
从压缩感知到稀疏表示 min 0 . . x s t Ax y = Ax y = • 矩阵的压缩感知模型就是一个线性矩阵方程组 • 假设原始高维信号为向量 ,低维测量向量为 y • 信号向量 x 与测量向量 y 满足线性组合关系 • 如果原始信号向量 x 具有稀疏性 x • 通过映射关系 获取高维信号 的低维采样 A A x y • 可以通过低维采样 b 对高维信号 x 进行恢复 信号的稀疏度:信号中非零元素个数 0 信号稀疏度量: 范数 x 0 l