
小波变换及其在图像处理 中的典型应用 赵丹培 宇航学院图像处理中心C座405 E-mail:zhaodanpei@buaa.edu.cn ■■■■ 2016年12月
小波变换及其在图像处理 中的典型应用 赵丹培 宇航学院图像处理中心C座405 E-mail: zhaodanpei@buaa.edu.cn 2016年12月

目录 8.1从傅里叶变换到小波变换的时频分析法 8.2小波变换分类 8.3小波变换的多分辨分析特性 8.4尺度函数与小波 8.5小波变换的快速实现 8.6图像的多分辨分解与重建 8.7小波变换在图像边缘检测中的应用 8.8小波变换在图像去噪中的应用 8.9小波变换在图像融合中的应用 2/116
目 录 8.1 从傅里叶变换到小波变换的时频分析法 8.2 小波变换分类 8.3 小波变换的多分辨分析特性 8.4 尺度函数与小波 2/116 8.5 小波变换的快速实现 8.6 图像的多分辨分解与重建 8.7 小波变换在图像边缘检测中的应用 8.8 小波变换在图像去噪中的应用 8.9 小波变换在图像融合中的应用

8.1从傅里叶变换到小波变换的 时频分析法 8.1.1傅里叶变换 Fourier变换一直是信号处理领域中应用最广泛、 效果最好的一种分析手段,是时域到频域互相转化的 工具,从物理意义上讲,傅里叶变换的实质是把对原 函数的研究转化为对其傅里叶变换的研究。但是傅里 叶变换只能提供信号在整个时间域上的频率,不能提 供信号在某个局部时间段上的频率信息。 3/116
Fourier变换一直是信号处理领域中应用最广泛、 效果最好的一种分析手段,是时域到频域互相转化的 8.1 从傅里叶变换到小波变换的 时频分析法 8.1.1 傅里叶变换 3/116 工具,从物理意义上讲,傅里叶变换的实质是把对原 函数的研究转化为对其傅里叶变换的研究。但是傅里 叶变换只能提供信号在整个时间域上的频率,不能提 供信号在某个局部时间段上的频率信息

8.1.1傅里叶变换 傅里叶变换:对于时域的常量函数,在频域 将表现为冲击函数,表明具有很好的频域局 部化性质。 F()=f(x)emdx 傅里叶变换 f(a)=)∫二F(odo= 反傅里叶变换 4/116
8.1.1 傅里叶变换 傅里叶变换:对于时域的常量函数,在频域 将表现为冲击函数,表明具有很好的频域局 部化性质。 4/116 j x F f x e dx 1 2 j x f x F e d 傅里叶变换 反傅里叶变换
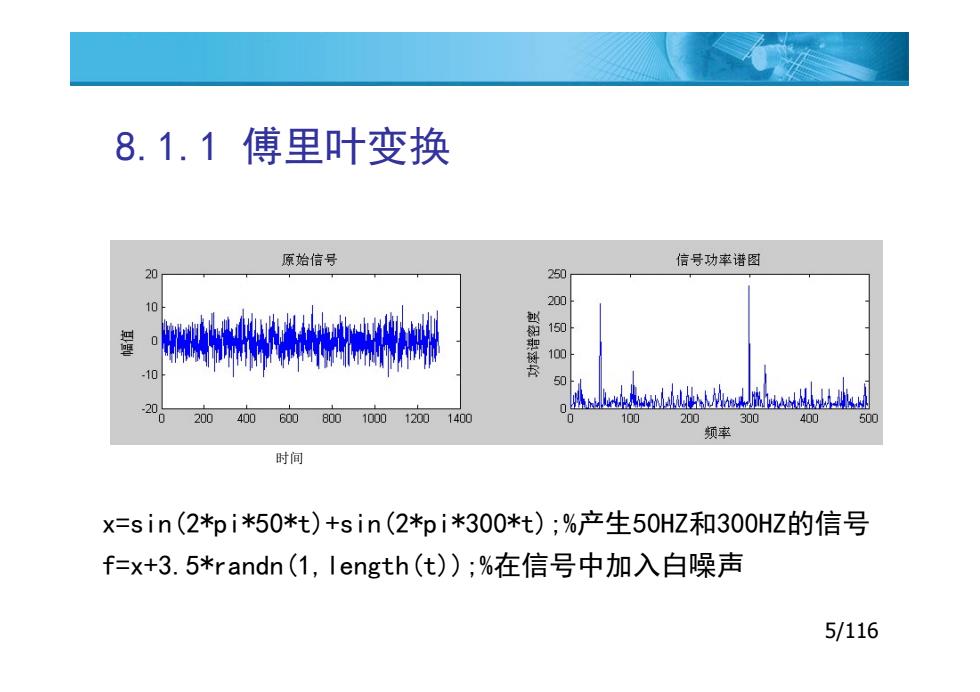
8.1.1傅里叶变换 原始信号 信号功率谱图 250 100 50 20 200400600800100012001400 100 200 300 400 500 频率 时间 x=sin(2*pi*50*t)+sin(2*pi*300*t);%产生50HZ和300HZ的信号 f=x+3.5*randn(1,length(t));%在信号中加入白噪声 5/116
8.1.1 傅里叶变换 5/116 x=sin(2*pi*50*t)+sin(2*pi*300*t);%产生50HZ和300HZ的信号 f=x+3.5*randn(1,length(t));%在信号中加入白噪声 时间

8.1.2短时傅里叶变换 由于傅立叶变换无法作局部分析,为此,人 们提出了短时傅里叶变换(STFT)的概念,即窗 口傅里叶变换。 短时傅里叶变换将整个时间域分割成一些小 的等时间间隔,然后在每个时间段上用傅里叶分 析,它在一定程度上包含了时间频率信息,但由 于时间间隔不能调整,因而难以检测持续时间很 短、频率很高的脉冲信号的发生时刻。 6/116
由于傅立叶变换无法作局部分析,为此,人 们提出了短时傅里叶变换(STFT)的概念,即窗 口傅里叶变换。 短时傅里叶变换将整个时间域分割成一些小 8.1.2 短时傅里叶变换 6/116 的等时间间隔,然后在每个时间段上用傅里叶分 析,它在一定程度上包含了时间频率信息,但由 于时间间隔不能调整,因而难以检测持续时间很 短、频率很高的脉冲信号的发生时刻

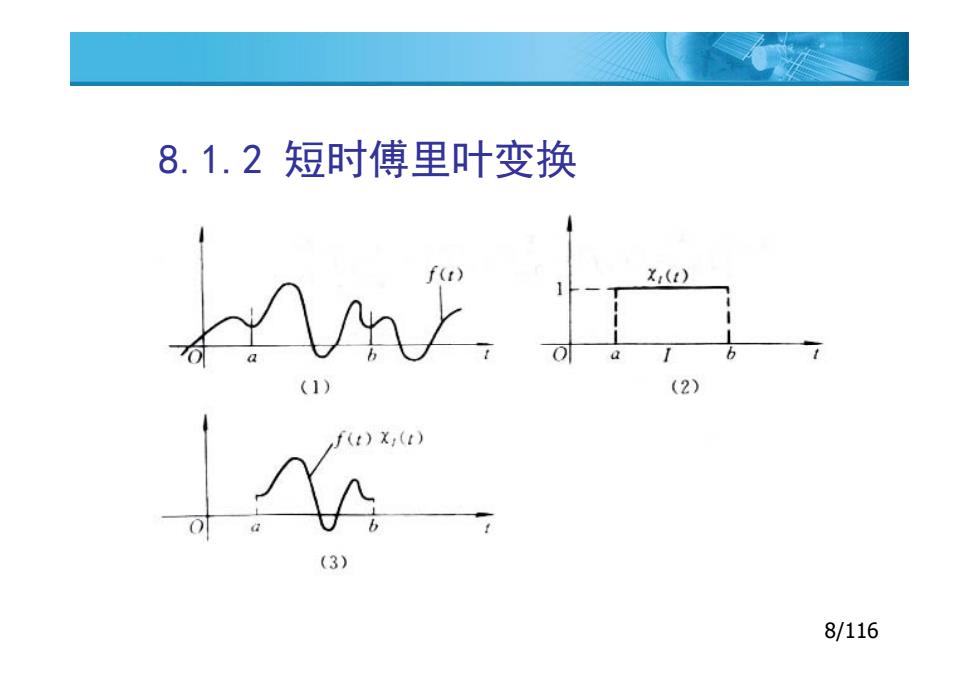
8.1.2短时傅里叶变换 。基本思想是:把信号划分成许多小的时间间隔,用 傅立叶变换分析每一个时间间隔,以便确定该时间 间隔存在的频率。 。STFT的处理方法是对信号施加一个滑动窗(反映滑动 窗的位置)后,再作傅立叶变换。即: STFT,o,)=f(d 时限 频限 7/116
8.1.2 短时傅里叶变换 基本思想是:把信号划分成许多小的时间间隔,用 傅立叶变换分析每一个时间间隔,以便确定该时间 间隔存在的频率。 STFT的处理方法是对信号施加一个滑动窗(反映滑动 7/116 STFT的处理方法是对信号施加一个滑动窗(反映滑动 窗的位置)后,再作傅立叶变换。即: ( , ) ( ) ( ) j t f STFT f t t e dt 时限 频限
8.1.2短时傅里叶变换 x:() (3) 8/116
8.1.2 短时傅里叶变换 8/116
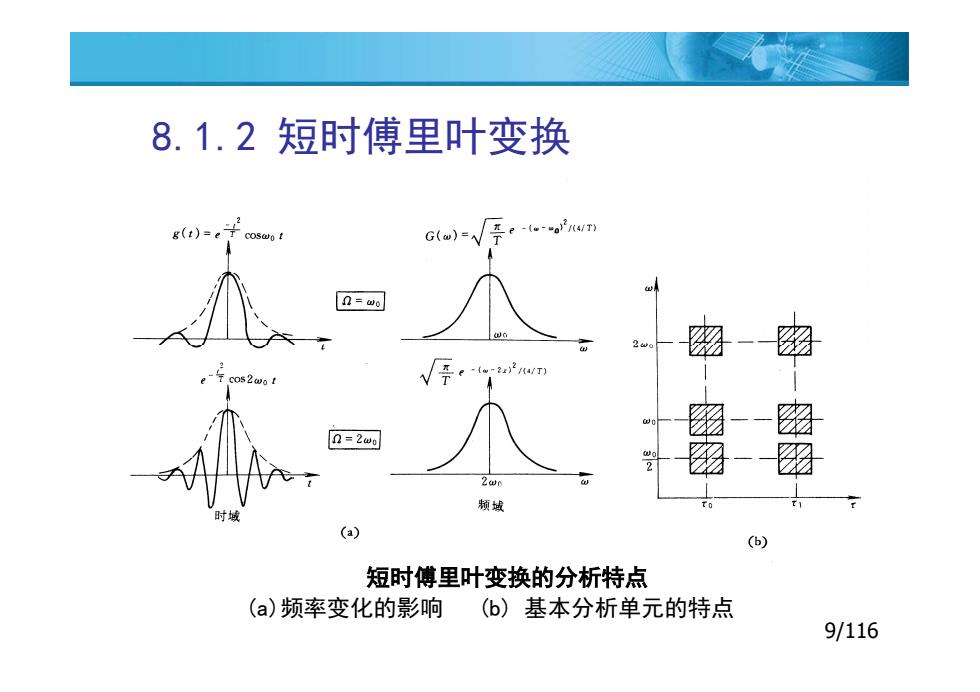
8.1.2短时傅里叶变换 g(t)=ecosw0 c()=√年o2wn 密 0=2w0 密 频域 (a) (b) 短时傅里叶变换的分析特点 (a)频率变化的影响(b)基本分析单元的特点 9/116
8.1.2 短时傅里叶变换 9/116 短时傅里叶变换的分析特点 (a)频率变化的影响 (b) 基本分析单元的特点

8.1.3小波变换 小波与傅里叶变换的区别: >从宏观上看,傅立叶分析是整体域分析,用单独的时 域或频域表示信号的特征; >从微观上看,小波变换与傅立叶变换的根本区别是由 小波和正弦波的不同局部化性质产生的; >小波分析具有局部化时频分析能力,能够提供一个随 频率改变的时间一频率窗口,用时域和频域的联合表 示信号的特征。 10/116
小波与傅里叶变换的区别: 从宏观上看,傅立叶分析是整体域分析,用单独的时 域或频域表示信号的特征; 从微观上看,小波变换与傅立叶变换的根本区别是由 8.1.3 小波变换 10/116 从微观上看,小波变换与傅立叶变换的根本区别是由 小波和正弦波的不同局部化性质产生的; 小波分析具有局部化时频分析能力,能够提供一个随 频率改变的时间-频率窗口,用时域和频域的联合表 示信号的特征