
第六章数学形态学在图像处理中的应用 6.1数学形态学概述 6.2数学形态学基本算法 6.3二值图像的形态学处理 6.4灰值形态学 教字图像处要 ■■■■
第六章 数学形态学在图像处理中的应用 6.1 数学形态学概述 6.2 数学形态学基本算法 6.3 二值图像的形态学处理 6.4 灰值形态学

6.1数学形态学概述 1、起源: 数学形态学(Mathematics Morphology)形成于 1964年,法国巴黎矿业学院马瑟荣(G.Matheron)和 其学生赛拉(J.Serra)从事铁矿核的定量岩石学分析, 提出了该理论。 数字图像处要 ■■■
1、起源: 数学形态学(Mathematics Morphology)形成于 1964年,法国巴黎矿业学院马瑟荣(G. Matheron)和 其学生赛拉(J. Serra)从事铁矿核的定量岩石学分析, 提出了该理论。 6.1 数学形态学概述

6.1数学形态学概述 2、发展: 数学形态学是一门建立在严格数学理论基础上的学 科,其基本思想和方法对图像处理的理论和技术产生了 重大的影响。目前,形态学图像处理已成为数字图像处 理的一个主要研究领域。在文字识别、显微图像分析、 医学图像、工业检测、机器人视觉都有很成功的应用。 教字图像处要 ■■■■
2、发展: 数学形态学是一门建立在严格数学理论基础上的学 科,其基本思想和方法对图像处理的理论和技术产生了 重大的影响。目前,形态学图像处理已成为数字图像处 理的一个主要研究领域。在文字识别、显微图像分析、 医学图像、工业检测、机器人视觉都有很成功的应用。 6.1 数学形态学概述

6.1数学形态学概述 3、定义: 数学形态学(Mathematical Morphology)是分析 几何形状和结构的数学方法,它建立在集合代数的基础 上,是用集合论方法定量描述目标几何结构的学科。 这种结构表示的可以是分析对象的宏观性质,例如, 在分析一个工具或印刷字符的形状时,研究的就是其宏 观结构;也可以是微观性质,例如,在分析颗粒分布或 由小的基元产生的纹理时,研究的便是微观结构。 教字图像处要 ■■
3、定义: 数学形态学(Mathematical Morphology)是分析 几何形状和结构的数学方法,它建立在集合代数的基础 上,是用集合论方法定量描述目标几何结构的学科。 这种结构表示的可以是分析对象的宏观性质,例如, 在分析一个工具或印刷字符的形状时,研究的就是其宏 观结构;也可以是微观性质,例如,在分析颗粒分布或 由小的基元产生的纹理时,研究的便是微观结构。 6.1 数学形态学概述

6.1数学形态学概述 4、形态学研究几何结构的基本思想 利用一个结构元素(相当于模板)去探测一个图像,看是 否能将这个结构元素很好地填放在图像的内部,同时验证填放 结构元素的方法是否有效。 对图像内适合放入结构元素的 位置做标记,得到关于图像结构的 信息。这些信息与结构元素的尺寸 和形状都有关。构造不同的结构元 素,便可完成不同的图像分析,得 形态学基本运算 到不同的分析结果。 教字图像处要 ■■■■
4、形态学研究几何结构的基本思想 利用一个结构元素(相当于模板)去探测一个图像,看是 否能将这个结构元素很好地填放在图像的内部,同时验证填放 结构元素的方法是否有效。 对图像内适合放入结构元素的 位置做标记,得到关于图像结构的 信息。这些信息与结构元素的尺寸 和形状都有关。构造不同的结构元 素,便可完成不同的图像分析,得 到不同的分析结果。 B 形态学基本运算 A 一、数学形态学概述 6.1 数学形态学概述

6.2数学形态学基本算法 1、基本概念 ●集合关系:设A和B为R的子集,A为物体区域,B 为某种结构元素,则B结构单元对A的关系有三类: a)B包含于ABGA b)B击中(hit)A, B∩A!=Φ c)B击不中(miss)A, B∩A=Φ B A B 包含、击中和击不中示意图 教字图像处要 ■■■■
1、基本概念 A B A B A B 包含、击中和击不中示意图 a) B 包含于A, b) B 击中(hit)A, c) B 击不中(miss)A, B A B A! =Φ B A =Φ 集合关系:设 A 和 B 为R 2的子集,A 为物体区域,B 为某种结构元素,则 B 结构单元对 A 的关系有三类: 6.2 数学形态学基本算法
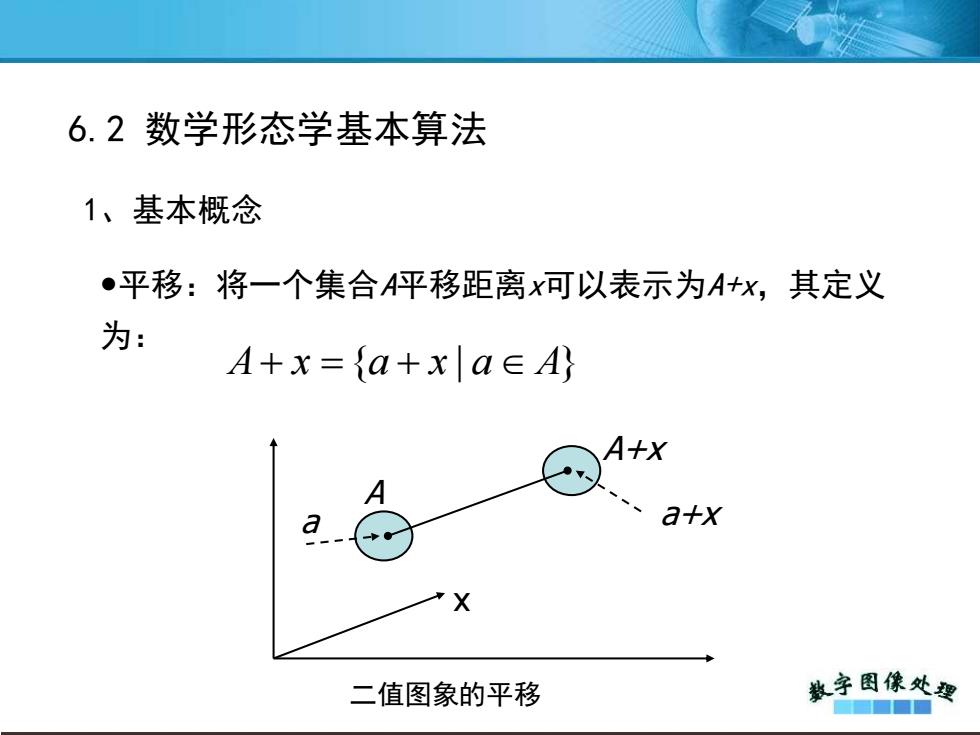
6.2数学形态学基本算法 1、基本概念 ●平移:将一个集合A平移距离x可以表示为A+x,其定义 为: A+x={a+x|a∈A} A+x a+x 二值图象的平移 教字图像处要 ■■■■
平移:将一个集合A平移距离x可以表示为A+x,其定义 为: A+ x ={a + x | a A} A A+x a a+x 二值图象的平移 x 1、基本概念 6.2 数学形态学基本算法

6.2数学形态学基本算法 1、基本概念 ●对称集:设有一幅图像A,将A中所有元素相对原点转 180°,即令(x,y)变成(-x,-y),所得到的新集合称为A 的对称集,记为-A. 相对原点转180° 数字图像处要 ■■■■
对称集:设有一幅图像A,将A中所有元素相对原点转 180o,即令(x,y)变成(-x,-y),所得到的新集合称为A 的对称集,记为-A. a -a A -A 相对原点转180o 1、基本概念 6.2 数学形态学基本算法

6.2数学形态学基本算法 2、腐蚀与膨胀 ·腐蚀 概念:腐蚀表示用某种“探针”(即某种形状的基元 或结构元素)对一个图象进行探测,以便找出在图象内部 可以放下该基元的区域。 定义:集合A被集合B腐蚀,表示为A⊙B,数学形 式为 AOB=x:B+xCA 教字图像处要 ■■■■
腐蚀 概念:腐蚀表示用某种“探针”(即某种形状的基元 或结构元素)对一个图象进行探测,以便找出在图象内部 可以放下该基元的区域。 定义:集合 A 被集合 B 腐蚀,表示为 ,数学形 式为 A B = {x : B + x A} A B 2、腐蚀与膨胀 6.2 数学形态学基本算法
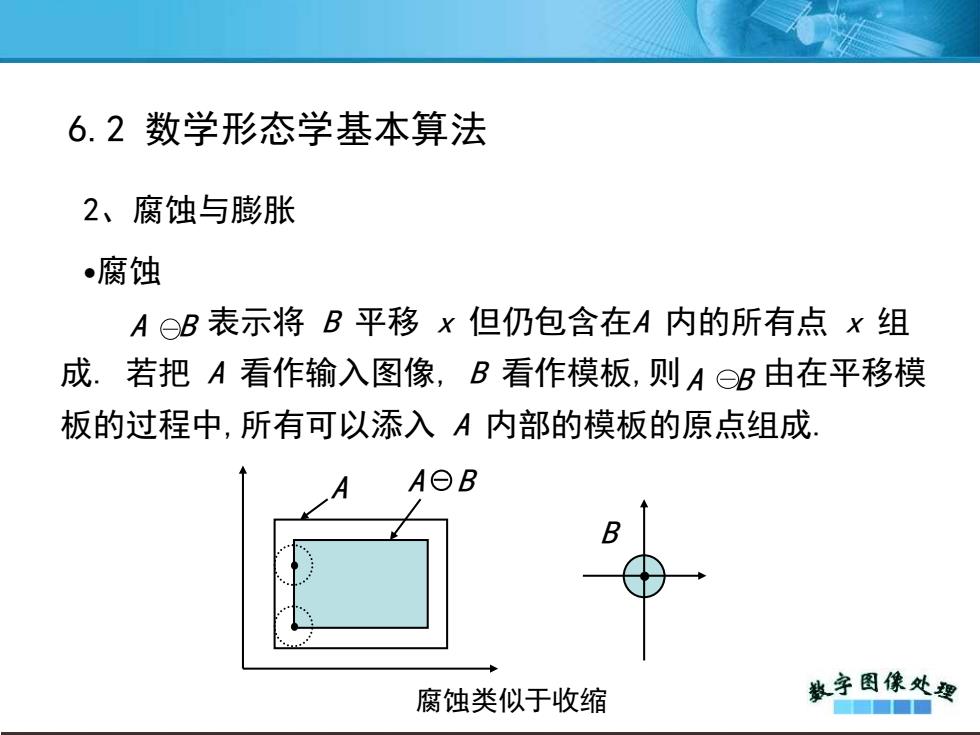
6.2数学形态学基本算法 2、腐蚀与膨胀 •腐蚀 AQB表示将B平移x但仍包含在A内的所有点x组 成.若把A看作输入图像,B看作模板,则A©B由在平移模 板的过程中,所有可以添入A内部的模板的原点组成: AOB 腐蚀类似于收缩 教字图像处要 ■■
腐蚀 表示将 B 平移 x 但仍包含在A 内的所有点 x 组 成. 若把 A 看作输入图像, B 看作模板,则 由在平移模 板的过程中,所有可以添入 A 内部的模板的原点组成. A B A B 2、腐蚀与膨胀 6.2 数学形态学基本算法 B 腐蚀类似于收缩 A A B