
北素航空航天大学 第三章投影变换与图像校正 3.1投影变换 3.2几何变换 3.3图像校正 3.4几何校正方法 教字图像处要
3.1 投影变换 3.2 几何变换 3.3 图像校正 3.4 几何校正方法 第三章 投影变换与图像校正

北京航空航天大学 3.1投影变换: 任一两坐标系:灭,7 x:P=[X1,X2,X3]T 7:P=[Y,Y2,Y3]I 令两坐标系方向余弦为: L11一一y,与x1之间的方向余弦(夹角余弦) L12一一y,与x2之间的方向余弦 L13一一y与×3之间的方向余弦 L一一y,与x,之间的方向余弦 教字图像处安
3.1 投影变换: X ,Y :P=[X1 ,X2 ,X3 ] T :P1 =[Y1 ,Y2 ,Y3 ] T 令两坐标系方向余弦为: L11--y1与x1之间的方向余弦(夹角余弦) L12--y1与x2之间的方向余弦 L13--y1与x3之间的方向余弦 ┋ Lij--yi与xj之间的方向余弦 X Y 任一两坐标系:

北京航空航天大学 得可与间关系: y1=L11X+L12X2+L13X3 y2=L21X1+L22X2+L23X3 y3=L31X1+L322+L33X3 如: yr Y-y2 R- L22 23 X= L31L32 x 则有Y=RX y1=L1X=|L1L12L13 X3 L1为X与y1之间的方向余弦 教字因像处要
得 Y 与 X 间关系: y1= L11 x1+ L12 x2+ L13 x3 y2= L21 x1+ L22 x2+ L23 x3 y3= L31 x1+ L32 x2+ L33 x3 如: y1 L1 L11 L12 L13 x1 Y= y2 R= L2 = L21 L22 L23 X= x2 y3 L3 L31 L32 L33 x3 则有Y = R X x1 y1= L1 X=∣L11 L12 L13∣ x2 x3 L1 为X与y1之间的方向余弦

北席航空航天大学 X2 X y X2 y2 X 1 教字国像处安
x 1 x 2 y 1 y 2 x x 1 x 2 y 1 y 2

北京航空航天大学 到二维空间来理解: x=x cos(B+Y) y2 x=x sin(B+Y) X2 y=x1 cosY+x2 cos(90-Y) x cos B y2 y Y y2=-x sinY+x cos Y 教字因像处要
到二维空间来理解: x1 =x cos(β+γ) x2 =x sin(β+γ) y1= x1 cosγ+ x2 cos(90°-γ) = x cosβ y2= - x1 sinγ+ x2 cosγ x1 x2 y1 y2 x γ β x1 x2 y1 y2
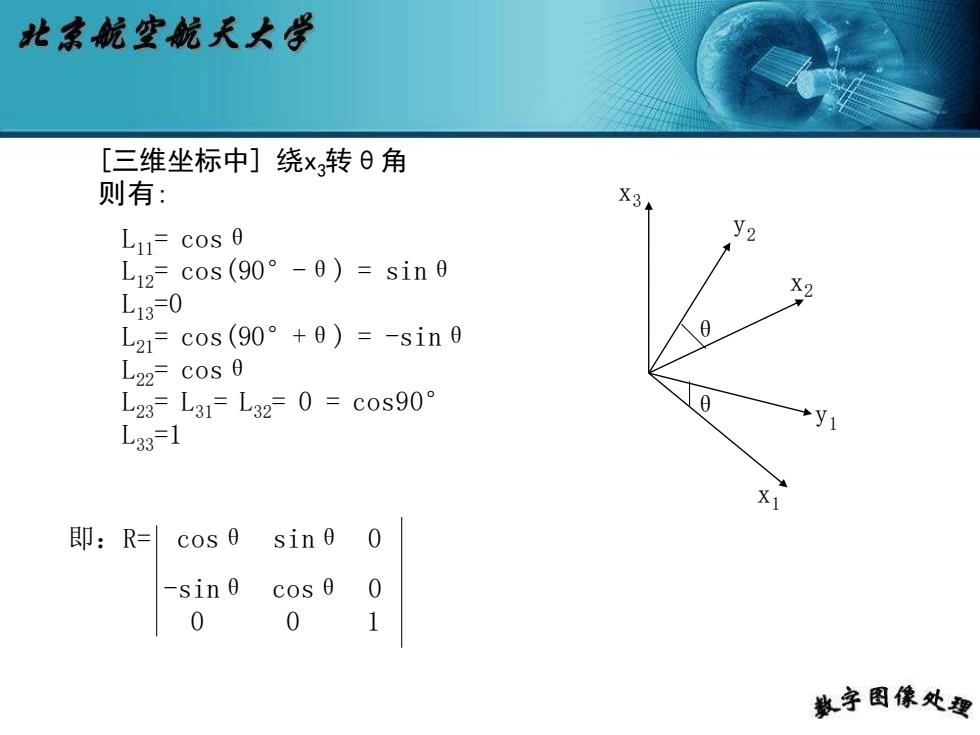
北京航空航天大学 [三维坐标中]绕x转0角 则有: X3 Lu=cos 0 L12c0s(90°-0)=sin0 ¥2 L13-0 L2cos(90°+0)=-sin0 L22=cos 0 L23=L31=L320=c0s90° 0 L331 1 即:R= cos 0 sin0 0 -sin 0 cos 0 0 0 0 1 教字图像处要
-sinθ cosθ 0 0 0 1 即:R= cosθ sinθ 0 [三维坐标中] 绕x3转θ角 则有: L11= cosθ L12= cos(90°-θ) = sinθ L13=0 L21= cos(90°+θ) = -sinθ L22= cosθ L23= L31= L32= 0 = cos90° L33=1 x2 x3 x1 y1 y2 θ θ

北素航空航天大学 矩阵正交条件: 含a6 引 或之aaw=8 旋转阵R为正交矩阵: 二维时: y1= cos0 sin0 y2 -sin0 cos0 X2 有: cos0 -sin0 sin0 cos0 教字因像处要
= = = = = = n k ki kj n k ik jk i j i j a a i j i j a a 1 1 0 1 或: 0 1 矩阵正交条件: 旋转阵R为正交矩阵: 二维时: y1 = cosθ sinθ x1 y2 -sinθ cosθ x2 有: x1 = cosθ –sinθ y1 x2 sinθ cosθ y2

北京航空航天大常 A 三维时: 有:L1m2+L122+L132=1 Q B A2 (cos2 a +cos2 B+cos2y )=A2 正交阵RT=Rl 有:X=RTY x1=L1y+L21y2+L31y3 X2=L12y1+L22y2+L32y3 X3=L13y1+L23y2+L33y3 教字国像处安
三维时: 有:L11 2 + L12 2 + L13 2 =1 β γ α A A2(cos2α+ cos2β+ cos2γ)= A2 正交阵 RT = R-1 有: X = RTY x1= L11y1+ L21y2+ L31y3 x2= L12y1+ L22y2+ L32y3 x3= L13y1+ L23y2+ L33y3
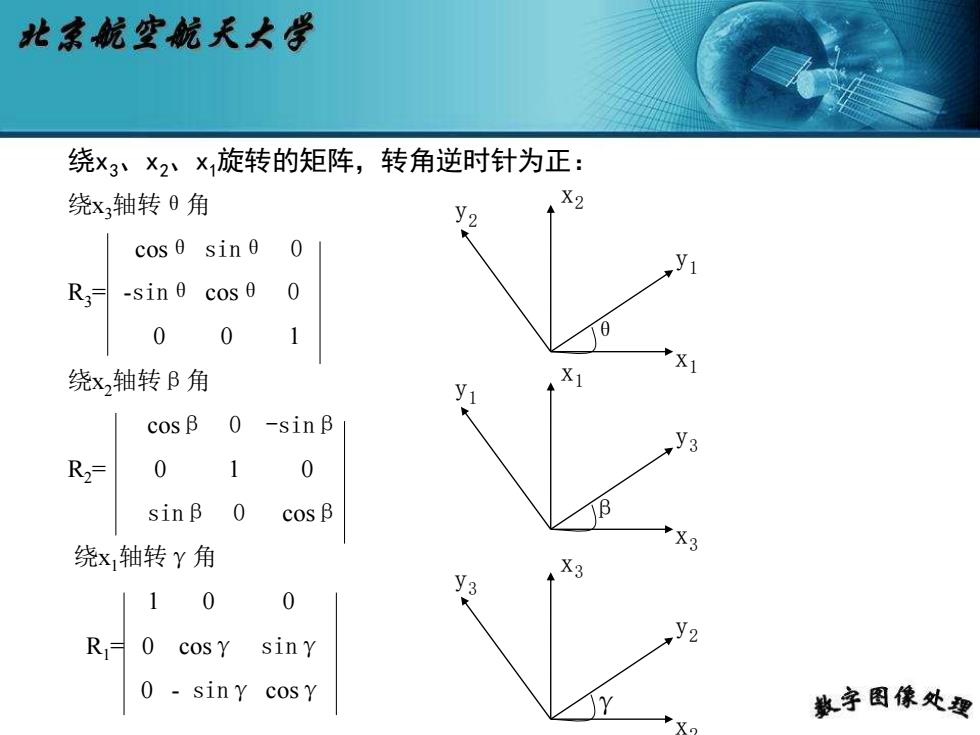
北京航空航天大增 绕x3、×2、x旋转的矩阵,转角逆时针为正: 绕x轴转0角 cos 0 sin 0 R -sin 0 cos 0 0 0 10 绕x轴转B角 cos B 0 -sinB R2= 0 1 0 sinB 0 cos B B 绕x轴转Y角 *X3 X3 0 0 R 0 cosy siny 0 -siny cosy 教字因像处要
绕x3、x2、x1旋转的矩阵,转角逆时针为正: 绕x3轴转θ角 cosθ sinθ 0 R3= -sinθ cosθ 0 0 0 1 绕x2轴转β角 cosβ 0 -sinβ R2= 0 1 0 sinβ 0 cosβ 绕x1轴转γ角 1 0 0 R1= 0 cosγ sinγ 0 - sinγ cosγ x2 y2 θ x1 y1 x3 y3 γ x2 y2 x1 y1 β x3 y3

北京航空航天大学 任意旋转: R=R,R(6,,k=1,2,3) 注意到: m11m12m13 R= m21m22 m23 只包括旋转。 m31 m32 m33 教字图像处安
任意旋转: R = R R R (i, j, k =1,2,3) i j k 注意到: m11 m12 m13 R = m21 m22 m23 只包括旋转。 m31 m32 m33