
北素航空航天大学 第二章有关数学基础 两方面问题: 抽象 物理现象 数学模型 数学工具:解决实际问题 教字图像处要
两方面问题: 抽象 物理现象 数学模型 数学工具:解决实际问题 第二章 有关数学基础

北京航空航天大学 第二章有关数学基础 2.1图像的向量表示 2.7其它常用变换 2.2随机场一图像的统计表示 2.8K-L变换 2.3正交变换 2.9图像的采样 2.4付氏变换 2.10二值图像的采样 2.5离散图像付氏变换(DFT) 2.11图像的量化 2.6快速付氏变换(FFT) 教字因像处爱
2.1 图像的向量表示 2.2 随机场-图像的统计表示 2.3 正交变换 2.4 付氏变换 2.5 离散图像付氏变换( DFT ) 2.6 快速付氏变换(FFT) 第二章 有关数学基础 2.7 其它常用变换 2.8 K-L变换 2.9 图像的采样 2.10 二值图像的采样 2.11 图像的量化
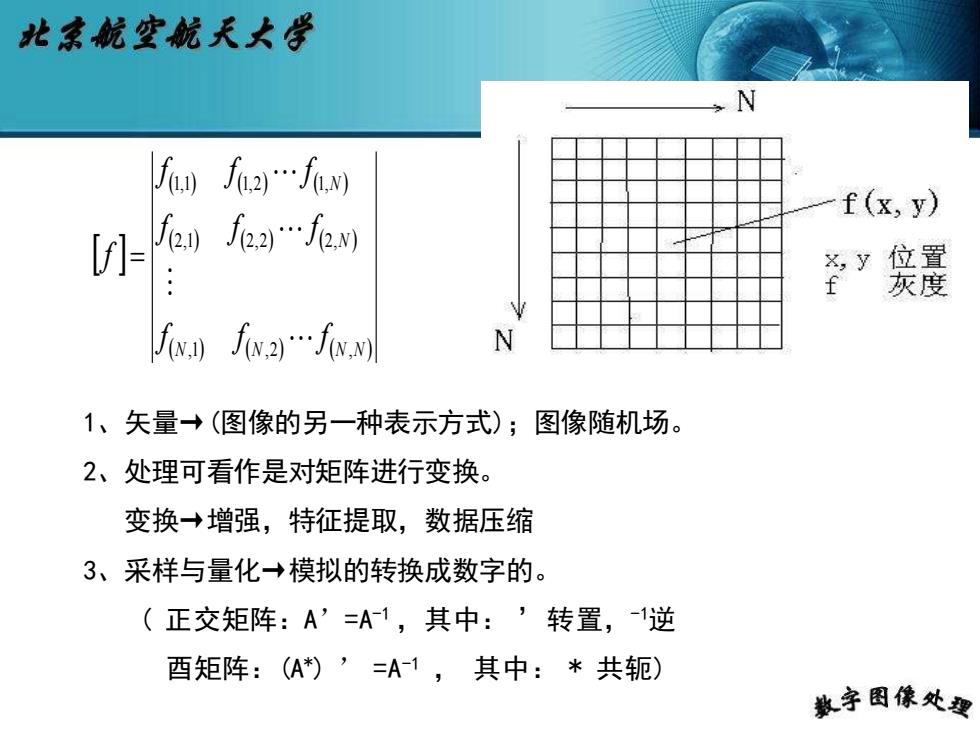
北京航空航天大皆 f创f2…fw f(x,y) fa)f…fan ×,y位置 f灰度 f f2…fn N 1、矢量→(图像的另一种表示方式);图像随机场。 2、处理可看作是对矩阵进行变换。 变换→增强,特征提取,数据压缩 3、采样与量化→模拟的转换成数字的。 (正交矩阵:A’=A1,其中:’转置,-1逆 酉矩阵:(A)’=A-1,其中:*共轭) 教字因像处要
( ) ( ) ( ) ( ) ( ) ( ) (N ) (N ) (N N ) N N f f f f f f f f f f ,1 ,2 , 2,1 2,2 2, 1,1 1,2 1, = 1、矢量→(图像的另一种表示方式);图像随机场。 2、处理可看作是对矩阵进行变换。 变换→增强,特征提取,数据压缩 3、采样与量化→模拟的转换成数字的。 ( 正交矩阵:A’=A-1 ,其中: ’转置,-1逆 酉矩阵:(A*) ’ =A-1 , 其中: * 共轭)

北席航空航天大常 2.1图像的向量表示 Ja.d) 二维图像矩阵 f2.) ffi2…fw f(N,) -创y fu,2) 表示成矢量 f= 形式为: fN,2) f则fx2fw NXN像素 fa.N) fN.N) 教字图像处要
二维图像矩阵 ( ) ( ) ( ) ( ) ( ) ( ) (N ) (N ) (N N ) N N f f f f f f f f f f ,1 ,2 , 2,1 2,2 2, 1,1 1,2 1, = 表示成矢量 形式为: 2.1 图像的向量表示 N×N像素 ( ) ( ) ( ) ( ) ( ) ( ) (N N ) N N N f f f f f f f f , 1, ,2 1,2 ,1 2,1 1,1 =1 2 N
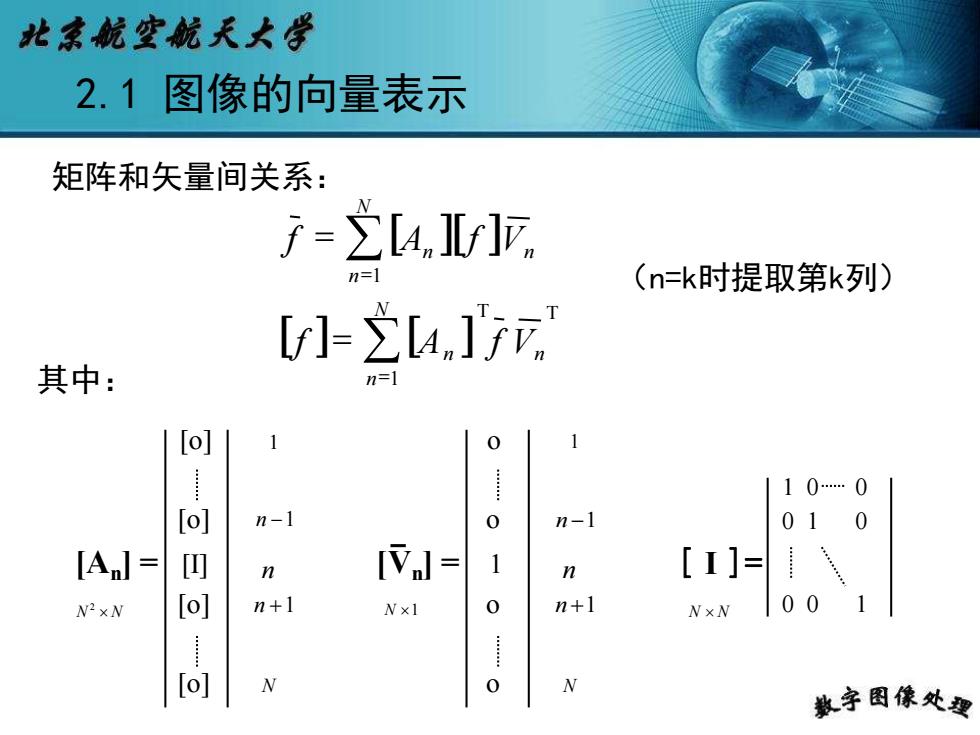
北京航空航天大学 2.1图像的向量表示 矩阵和矢量间关系: f=之4Lf]。 n=l (n=k时提取第k列) [l-. 其中: [o] 0 110…0 [o] n-1 0 n-1 010 [An]= 四 n [V]= 1 n [1]= N2×N [o] n+1 N×1 0 n+1 N×N00 [o] 0 教字图像处要
矩阵和矢量间关系: (n=k时提取第k列) 2.1 图像的向量表示 [o] [o] [An ] = [I] [o] [o] N N 2 1 n −1 n n +1 N o o [Vn ] = 1 o o N 1 1 n −1 n n +1 N 其中: 1 0 0 0 1 0 [ I ]= N N 0 0 1 = = = = N n n n N n n n f A f V f A f V 1 1 T T

北京航空航天大常 2.1图像的向量表示 当输入输出图像均为向量表示时,则处理之可表示为: g [tlf 此处8和∫可能不同维数 如:M2×1 N2X1 [T]为M2XN2 教字国像处安
当输入输出图像均为向量表示时,则处理之可表示为: g = T f 2.1 图像的向量表示 此处 和 可能不同维数 如: M 2×1 N2×1 [T]为M 2×N 2 g f

北京航空航天大学 2.1图像的向量表示 也可表示为: pq)=∑∑p,gm小f6m,) 其中:p=1..M,q=1,2..M 总之,图像三种表达方式:矩阵、矢量和 ∑,如g=∑… 教字图像处要
也可表示为: 其中:p=1…M, q=1,2…M ( ) ( ) ( ) = = = N n N m g p q t p q m n f m n 1 1 , , , , 2.1 图像的向量表示 总之,图像三种表达方式:矩阵、矢量和 ∑,如gij=∑…

北京航空航天大学 2.2随机场 一一图像的统计表示 一幅图像并不是全图各部分特征都相同,相同了则无信息, 不同才有信息。任一图像,其特征为随机的,且全场各部分间 也不均匀(随机的),不存在全图统一的特征。 图像可作为二维随机场中一个样本来分析。在某些场合使 用确定的表示来描述图像有困难,然而用平均特性能方便地描 述,如描述纹理结构图象可能很方便。 由于图像为实函数,可认为是二维实随机场。 教字因像处爱
一幅图像并不是全图各部分特征都相同,相同了则无信息, 不同才有信息。任一图像,其特征为随机的,且全场各部分间 也不均匀(随机的),不存在全图统一的特征。 图像可作为二维随机场中一个样本 来分析。在某些场合使 用确定的表示来描述图像有困难,然而用平均特性能方便地描 述,如描述纹理结构图象可能很方便。 由于图像为实函数,可认为是二维实随机场。 2.2 随机场--图像的统计表示

北京航空航天大学 2.2随机场一一 图像的统计表示 一个图像完备集包含所有图像,任一图像可看作其中一个 样本,图像集可看作随机场,在此集中某一像素亮度f,随x,y而 变化。 对确定的(xo,yo)其值又随i而变化(i为第i幅图),即任一点 f:(xo,yo)均为随机变量,每一点均可用统计特性来描述。 随机场中特定(x,yo)为一随机变量,对场上所有(x,y), 不一定具有相同的统计特性,即f(x,y)之分布函数与(x,y)密 度函数有关。 令P{f(x,y)<z}代表f(x,y)<z之概率,随机变量f(x,y) 在点(x,y)处分布函数表为: e(z;x,y)=pif(x,y)(z 教字图像处要
一个图像完备集包含所有图像,任一图像可看作其中一个 样本,图像集可看作随机场,在此集中某一像素亮度fi随x,y而 变化。 对确定的(x0 ,y0 )其值又随i而变化(i为第i幅图),即任一点 fi (x0 ,y0 )均为随机变量,每一点均可用统计特性来描述。 随机场中特定(x0 ,y0 )为一随机变量,对场上所有(x,y), 不一定具有相同的统计特性,即f(x,y)之分布函数与(x, y)密 度函数有关。 令P{f(x,y)<z} 代表 f(x,y)<z 之概率,随机变量f(x,y) 在点(x,y)处分布函数 表为: (z; x, y) = pf (x, y) z 2.2 随机场--图像的统计表示

北京航空航天大学 2.2随机场 一一图像的统计表示 f(x,y)在(x,y)密度函数: (x以p以 02 总体平均特征: 随机场均值函数(各点均值不同): m,(x.y)=Elf(x.y)[=x.y)d 在(x,y)处均值是(x,y)的函数 方差函数:6(x,y)=Ef(x,y)-m(x,y} 教字因像处爱
f(x,y)在(x,y)处密度函数: ( ) ( ) z x y z x y = , ; , 总体平均特征: 随机场均值函数(各点均值不同): ( ) ( ) ( ) − m x y = E f x y = z z x y dz f , , ; , 在(x,y)处均值是(x,y)的函数 方差函数 : ( ) ( ) ( ) 2 2 x, y E f x, y m x, y f = − f 2.2 随机场--图像的统计表示