
Chapter 7 The electronic theory of metal Objectives At the end of this Chapter,you should: 1.Understand the physical meaning of Fermi statistical distribution function. 2.Be able to calculate the Fermi level at 0 K. 3.Understand the concept of work function and contact potential. 4.Be able to calculate the heat capacity of electrons for metals
Chapter 7 The electronic theory of metal Objectives At the end of this Chapter, you should: 1. Understand the physical meaning of Fermi statistical distribution function. 2. Be able to calculate the Fermi level at 0 K. 3. Understand the concept of work function and contact potential. 4. Be able to calculate the heat capacity of electrons for metals

7.1 Fermi statistics and the heat capacity of electron The function of Fermi distribution For the equilibrium state of one system,the basic principle of Fermi statistics can be 1 f(E)=eF-+1 Which the probability that the eigenstate at energy E will be occupied by an electron
7.1 Fermi statistics and the heat capacity of electron For the equilibrium state of one system, the basic principle of Fermi statistics can be k 1 ( ) 1 E E T F B f E e − = + Which the probability that the eigenstate at energy E will be occupied by an electron. The function of Fermi distribution

The function of Fermi distribution f(E)has the form 1)E=Ee,f(E)=1/2 E 2)When E is higher than Er by several kBT, T=0K e5-Ee/kr>1,f(E)≈0 such eigenstate is almost empty; 3)When E is lower than Er by several kpT, 0.5 1f(E) eB-Erkr<l,f(E)≈1 The function of shows that the function f(E)changes from Fermi distribution value 1 to value 0 within the scope of several kBT up and down Er
The function of Fermi distribution f (E) has the form , ( ) 1 2 E E f E = = F 1, ( ) 0 E E k T F B e f E − k 1, ( ) 1 E E T F B e f E − The function of shows that the function f (E) changes from Fermi distribution value 1 to value 0 within the scope of several kBT up and down EF . such eigenstate is almost empty; 3) When E is lower than EF by several kBT, 2)When E is higher than EF by several kBT, 1)

The image left is the situation at 0 K,and the right is the situation at TK. Fermi distribution specifically shows the situation of thermal excitation.the change of Fermi distribution from OK to TK shows that some electrons at energy below E transfer to the higher state at energy above E after getting the energy with the magnitude being kBT. 0K TK Fermi surface and thermal excitation
The image left is the situation at 0 K, and the right is the situation at T K. Fermi distribution specifically shows the situation of thermal excitation. the change of Fermi distribution from 0K to TK shows that some electrons at energy below transfer to the higher state at energy above after getting the energy with the magnitude being kBT. Fermi surface and thermal excitation 0 EF 0 EF 0 EF

Density of States N(E) We often need to know the density of electron states,which is the number of states per unit energy,so we can quickly calculate it: The differential number of electron states in a range of energy dE or wavevector dk is: dN N(EdE=N(k)dk N(E)=N(k d_N(k)_V/8π3mV dEdE/dk2k/m28π3k Now using the general relation: 1/2 k=司 2mE we get: C2mE)
Density of States N(E) We often need to know the density of electron states, which is the number of states per unit energy, so we can quickly calculate it: dN = N(E)dE = N(k)dk k mV k m V dE dk N k dE dk N E N k 2 2 3 3 / 8 /8 / ( ) ( ) ( ) = = = = Now using the general relation: 1/ 2 2 2 = mE k we get: ( ) 1/ 2 3 2 3 ( ) 2m E V N E = The differential number of electron states in a range of energy dE or wavevector dk is:

Utility of the Density of States With N(E)we can immediately 「N(E)EdE calculate the average energy per (E〉= total energy 0 electron in the 3-D FEG system: electrons N(E)dE We can simplify by using the N(E)=CE12 relation: 2 EF N(E) C∫EndE E5/2 5 (E〉= 0 0 3 E 2 C E2 dE E32 3 Er Why the factor 3/5?Alook at the density of states curve should give the answer:
Utility of the Density of States We can simplify by using the relation: With N(E) we can immediately calculate the average energy per electron in the 3-D FEG system: Why the factor 3/5? A look at the density of states curve should give the answer: = = F F E E N E dE N E E dE electrons total energy E 0 0 ( ) ( ) # 1/ 2 N(E) = CE E F E E E E E E C E dE C E dE E F F F F 5 3 3 2 5 2 0 3/ 2 0 5/ 2 0 1/ 2 0 3/ 2 = = = N(E) E EF
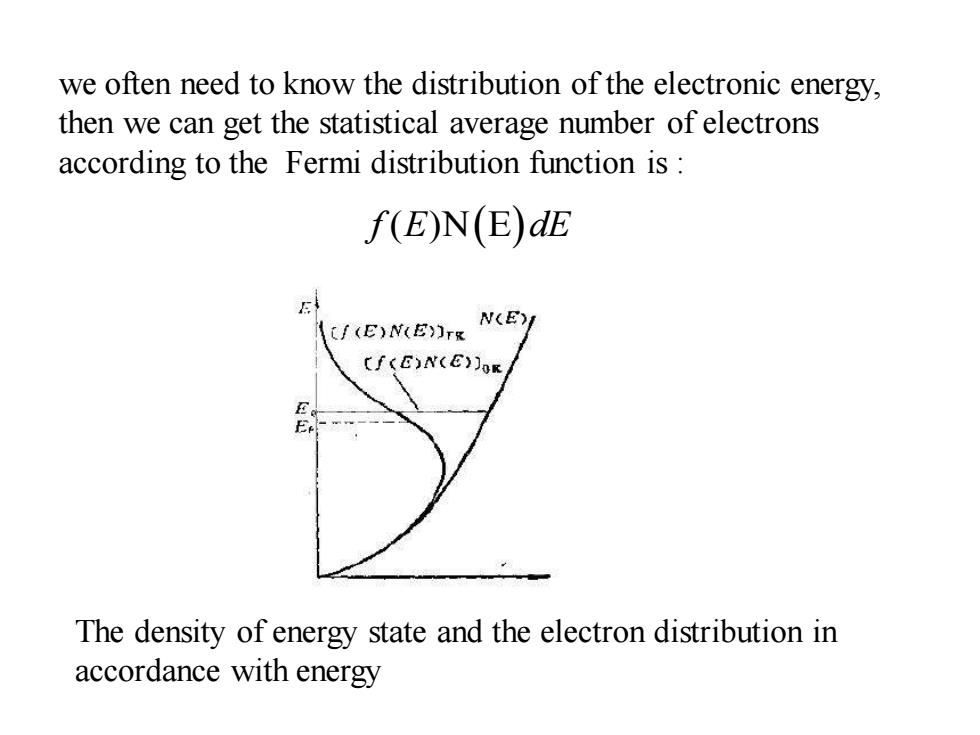
we often need to know the distribution of the electronic energy, then we can get the statistical average number of electrons according to the Fermi distribution function is: f(E)N(E)dE N(E) (E)N(E)rg Cf(E)N(E)JoR The density of energy state and the electron distribution in accordance with energy
The density of energy state and the electron distribution in accordance with energyf E dE ( )N E( ) we often need to know the distribution of the electronic energy, then we can get the statistical average number of electrons according to the Fermi distribution function is :

Determination of Er In the system,the total number of electron is given by N=f(E)N(E)dE Introducing a new function (E)=fN(E)dE Q(E)means the total number of the quantum states with energy above E. Then we can obtain N-E5)) Because Q(E)=0 when E-0,and f(E)-0 when E=oo,The first is zero.So af dE
Determination of EF ( ) 0 N f E dE ( )N E = ( ) 0 ( ) N E E Q E dE = 0 ( ) ( ) ( ) 0 N f E Q E Q E dE f E + = − In the system , the total number of electron is given by 0 N Q E( ) E E f d = − Introducing a new function Because Q(E) =0 when E=0, and f (E)=0 when E=∞, The first is zero. So Q (E) means the total number of the quantum states with energy above E. Then we can obtain

Fuction has the characteristic of 8 function,and its contribution to the integral mainly comes from E nearby Ee. of OE We can perform Taylor expansion on E Q(E)near E,Er electrons can be approximately given for nearly free by f(E Er E 12 f(E) the characteristic of It is obvious that the energy at Fermi surface has slight decrease (about 1/10000)when the temperature is increased,but the slight decline has a decisive effect on the metal properties
Function has the characteristic of δ function, and its contribution to the integral mainly comes from E nearby EF . We can perform Taylor expansion on Q(E) near EF , EF electrons can be approximately given for nearly free by f E − 2 2 2 2 0 0 0 1 1 12 12 B F F F F F k T T E E E E T = − = − It is obvious that the energy at Fermi surface has slight decrease (about 1/10000) when the temperature is increased, but the slight decline has a decisive effect on the metal properties. the characteristic of f E −

The heat capacity of electron 19th century puzzle:each monatomic gas molecule in sample at temperature T3kT has energy E=N(k),so if the N free electrons in a metal make up a classical "gas"they should behave similarly. 月-7-N,k灯-m n n So the electronic contribution to the molar heat capacity would be expected to be d(Ea Ca-arn =多R This is half of the 3R we found for the lattice heat capacity at high T.But experiments show that the total C for metals is only slightly higher than for insulatorswhich conflicts with the classical theory!
So the electronic contribution to the molar heat capacity would be expected to be k T N k T RT n N n E A el 2 3 2 3 2 3 = = = R n E dT d C el el 2 3 = = This is half of the 3R we found for the lattice heat capacity at high T. But experiments show that the total C for metals is only slightly higher than for insulators—which conflicts with the classical theory! ( ) 2 3 Eel = N kT 19th century puzzle: each monatomic gas molecule in sample at temperature T has energy , so if the N free electrons in a metal make up a classical “gas” they should behave similarly. kT 2 3 The heat capacity of electron